Efficient implementation of Smolyak sparse grid with nonnested

Efficient implementation of Smolyak sparse grid with nonnested grids Methodologies, coordinates, KEO A. Perveaux (ex doc) M. Ndong (ex post-doc) F. Gatti (Montpellier) 1 Photo-processes B. Lasorne (Montpellier) H. -D. Meyer (Heidelberg) A. Nauts (Louvain-La-Neuve) Banff 2016 Spectroscopy J. M. Luis (Girona) B. Kirtman (Santa Barbara) H. Reis (Αθήνα)

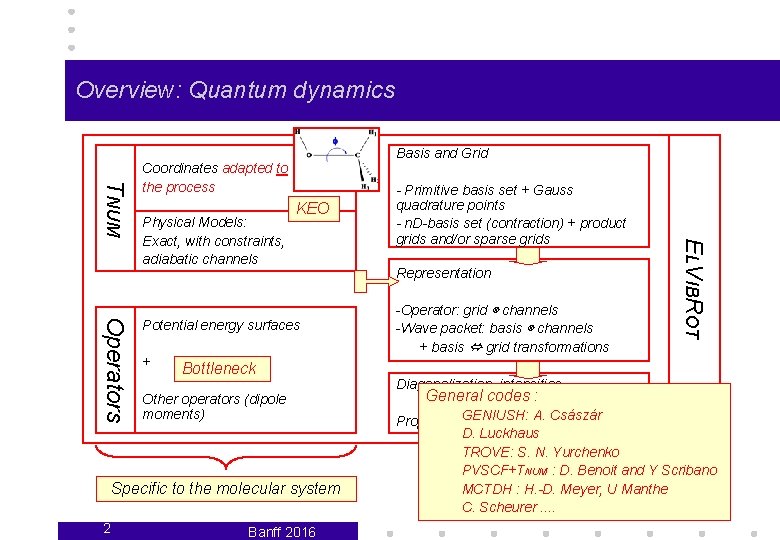
Overview: Quantum dynamics Basis and Grid TNUM Coordinates adapted to the process KEO Operators Potential energy surfaces + Bottleneck Other operators (dipole moments) Specific to the molecular system 2 Banff 2016 Representation -Operator: grid ⊗ channels -Wave packet: basis ⊗ channels + basis ⇔ grid transformations ELVIBROT Physical Models: Exact, with constraints, adiabatic channels - Primitive basis set + Gauss quadrature points - n. D-basis set (contraction) + product grids and/or sparse grids Diagonalization, intensities. . . General codes : GENIUSH: A. Császár Propagation, optimal control D. Luckhaus TROVE: S. N. Yurchenko PVSCF+TNUM : D. Benoit and Y Scribano MCTDH : H. -D. Meyer, U Manthe C. Scheurer. .

How to get the analytical expressions of T? Several routes to obtain a Kinetic Energy Operator • Using the Jacobian matrices to get the metric tensors[1, 2]: : Contravariant components of metric tensor Used for the numerical implementation[3] (TNUM[4]). • Using the conjugate momenta, vectors, [5, 6, 8]: , associated with the [1] B. Podolsky, Phys. Rev. 32, 812 (1928). [2] A. Nauts and X. Chapuisat, Mol. Phys. 55, 1287 (1985). [3] J. Laane et al. , JMS 1982, 91, p 286 [4] D. Lauvergnat et A. Nauts, JCP 116, p 8560 (2002). [5] X. Chapuisat, C. Iung, Phys. Rev. A 45, 6217– 6235 (1992). 3 Banff 2016 Used for the analytical expression / implementation (TANA[7]). [6] F. Gatti, C. Iung Phys. Rep. 484 1– 69 (2009). [7] M. Ndong, L. Joubert-Doriol, H. -D. Meyer, A. Nauts, F. Gatti, D. Lauvergnat, JCP 136, p 034107, (2012). [8] Wang and Carrington, JCP 113, 7097 (2000).

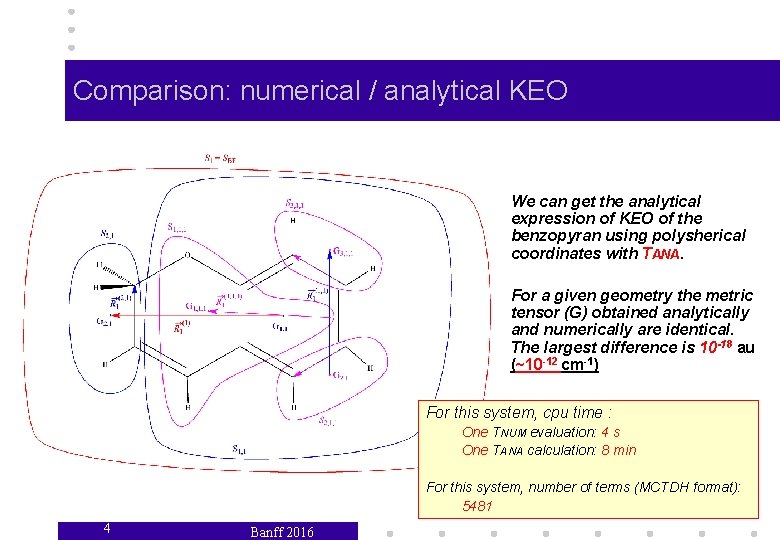
Comparison: numerical / analytical KEO We can get the analytical expression of KEO of the benzopyran using polysherical coordinates with TANA. For a given geometry the metric tensor (G) obtained analytically and numerically are identical. The largest difference is 10 -18 au (~10 -12 cm-1) For this system, cpu time : One TNUM evaluation: 4 s One TANA calculation: 8 min For this system, number of terms (MCTDH format): 5481 4 Banff 2016

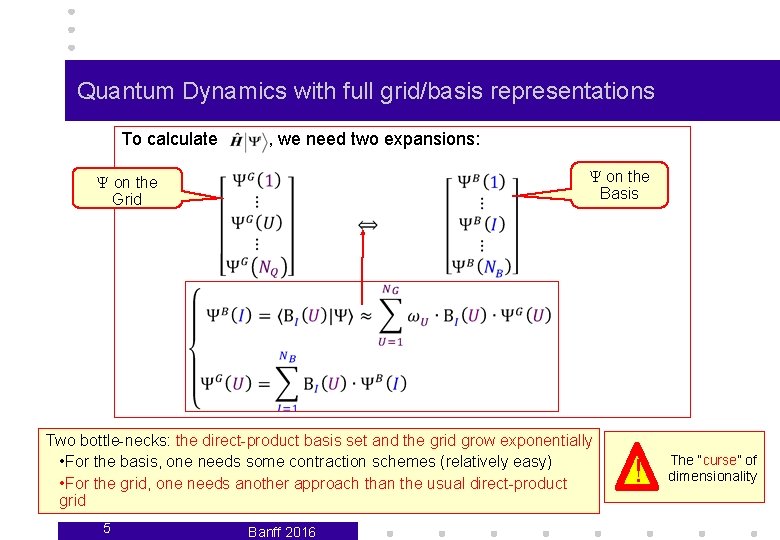
Quantum Dynamics with full grid/basis representations To calculate , we need two expansions: Y on the Basis Y on the Grid Two bottle-necks: the direct-product basis set and the grid grow exponentially • For the basis, one needs some contraction schemes (relatively easy) • For the grid, one needs another approach than the usual direct-product grid 5 Banff 2016 ! The “curse” of dimensionality

non-DP basis Basis functions are still expressed as a product: but they are selected such that: Ex 1: selection in terms of excitation or polynomial degree: Ex 2: other selection: 6 1 2 3 4 5 6 7 0 0 0 1 1 2 2 Banff 2016 Selection equivalent to the pruned basis set of T. Carrington

Basis ⇒ Grid, with non-DP Basis and DP Grid: Efficient way Using partial transformation for a given, k: loop on k Remark: with a DP basis: ! The number of operations is smaller: Ex: LB=9 and nq=10 with n=9 7 DPB/DPG NB NG n. Op yes/yes 109 90. 109 no/yes 48620 109 18. 7 109 Banff 2016 ! The “curse” of dimensionality

Smolyak grid: non-DP grid A weighted sum of small DP Grids (instead of a single and large DP Grid) The • • • define the size of the grids similarly to the non-DP basis functions: Series in Nested grids: S. A. Smolyak Soviet Mathematics Doklady, 1963, 4, 240. Avila, G. ; Carrington, T. JCP, 2009, 131, pp 174103 (6 D 12 D) 8 Banff 2016 V. Gradinaru, SIAM J. Numer. Anal. , 2008, 46, p 103. J. Burkardt : http: //people. sc. fsu. edu/~jburkardt/presentations

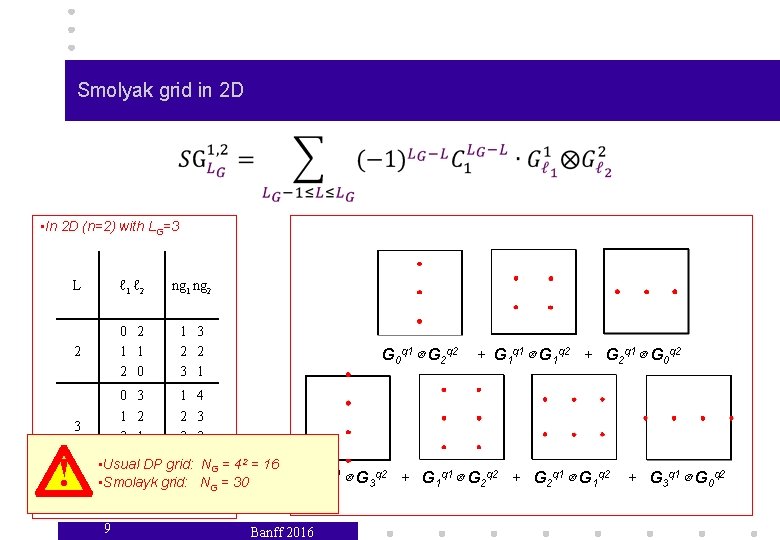
Smolyak grid in 2 D • In 2 D (n=2) with LG=3 L ℓ 1 ℓ 2 ng 1 ng 2 2 0 2 1 1 2 0 1 3 2 2 3 1 3 ! G 0 q 1 ⊗ G 2 q 2 0 3 1 4 1 2 2 3 2 1 3 2 3 0 4 1 • Usual DP grid: NG = 42 = 16 • Smolayk grid: NG = 30 9 + G 1 q 1 ⊗ G 1 q 2 + G 2 q 1 ⊗ G 0 q 2 G 0 q 1 ⊗ G 3 q 2 + G 1 q 1 ⊗ G 2 q 2 + G 2 q 1 ⊗ G 1 q 2 Banff 2016 + G 3 q 1 ⊗ G 0 q 2

Basis Grid, with Smolyak grid: Obvious way For each DP grid, we can use the previous transformation for non-DP basis and DP grid. Number of operations with LB=9 and LG=9 with n=9 DPB/DPG NB NG n. Op yes/yes 109 90. 109 no/yes 48620 109 18. 7 109 no/no 48620 1. 6 106 2. 1 109 Avila and Carrington JCP, 2009, 131, pp 174103 (6 D 12 D) Lauvergnat and Nauts, Spectrochim. Acta Part A, 119, 18 (2014). 10 Banff 2016 3 x 3 D (n=3)

Basis Grid, with Smolyak grid: Obvious way For each DP grid, we can use the previous transformation for non-DP basis and DP grid. ! With this implementation, we are doing several times the same calculations. How to overcome this problem? Avila and Carrington implementation with nested grids Our first implementation with n. D grid for (the problem is only reduced) New implementation Avila and Carrington JCP, 2009, 131, pp 174103 (6 D 12 D) Lauvergnat and Nauts, Spectrochim. Acta Part A, 119, 18 (2014). 11 Banff 2016

Sequential Basis ⇒ Grid transformation, with Smolyak grid: New way Using partial transformation for a given, k: loop on k 1. 2. 3. 4. For k=n, the first sum has ONE term (Y on the basis only) Then, the number of terms increases as the Smolyak grid is built. For k=1, the double sum gives the full Smolyak grid. Each contribution has to be weighted with the Smolyak weight. At a given k, this procedure is equivalent to sum on all grid points of a partial Smolyak grid with [k. . . n] 12 Banff 2016

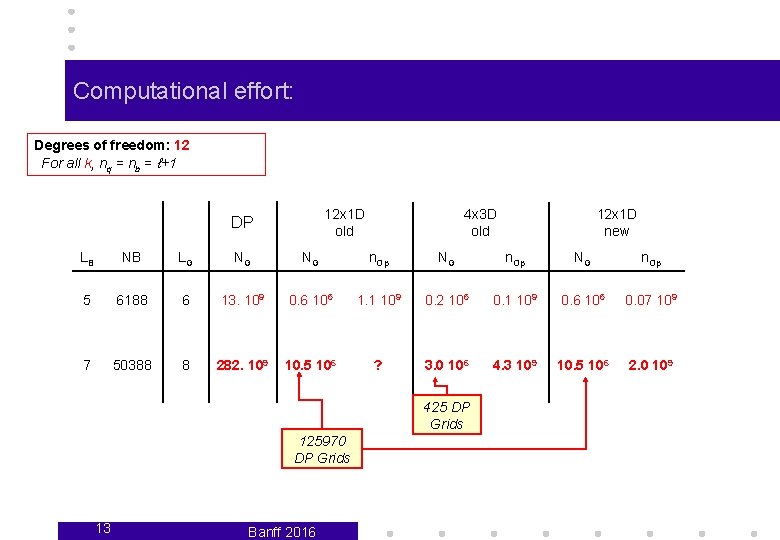
Computational effort: Degrees of freedom: 12 For all k, nq = nb = ℓ+1 12 x 1 D old DP 4 x 3 D old 12 x 1 D new LB NB LG NG NG n. Op 5 6188 6 13. 109 0. 6 106 1. 1 109 0. 2 106 0. 1 109 0. 6 106 0. 07 109 7 50388 8 282. 109 10. 5 106 ? 3. 0 106 4. 3 109 10. 5 106 2. 0 109 425 DP Grids 125970 DP Grids 13 Banff 2016

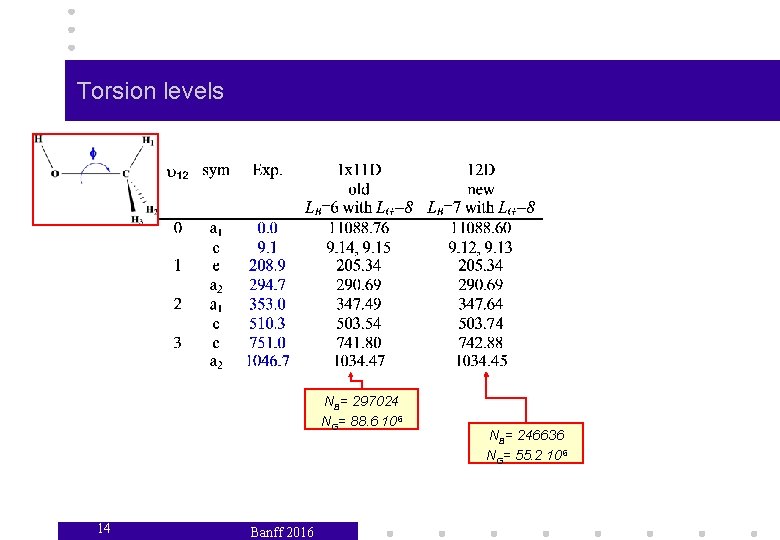
Torsion levels NB= 297024 NG= 88. 6 106 14 Banff 2016 NB= 246636 NG= 55. 2 106

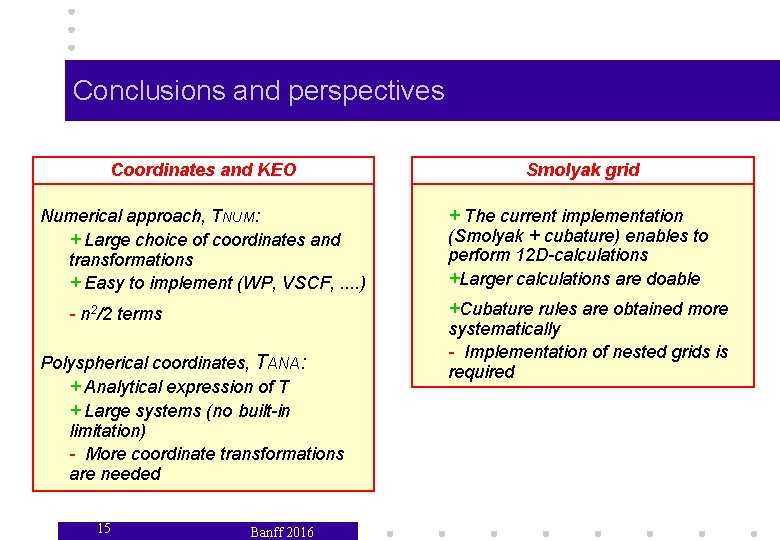
Conclusions and perspectives Coordinates and KEO Smolyak grid Numerical approach, TNUM: + Large choice of coordinates and transformations + Easy to implement (WP, VSCF, . . ) + The current implementation (Smolyak + cubature) enables to perform 12 D-calculations +Larger calculations are doable - n 2/2 terms Polyspherical coordinates, TANA: + Analytical expression of T + Large systems (no built-in limitation) - More coordinate transformations are needed 15 Banff 2016 +Cubature rules are obtained more systematically - Implementation of nested grids is required

Thank you! 16 Banff 2016

Notations Basis functions, BI(U), are expressed as a product of n basis functions: Not necessarily 1 D For the wave functions : on the basis on the grid partial on the basis and the grid 17 Banff 2016

Basis Grid, with direct-product Basis and grid: Naive way Using directly, the NB basis functions, BI(U), on the NG grid points: Value of the basis function I on the grid point U Number of operations (multiplications): B⇒Q: ⇒ n. Op = NB x NG IF 18 ⇒ n. Op = ng 2 n Banff 2016 This number could be reduced

Basis ⇒ Grid, with direct-product Basis and Grid: Efficient way Using partial transformation for a given, k: loop on k In total, n. Op: IF ⇒ Light and Carrington Adv. Chem. Phys. 114, 263 (2000). 19 Banff 2016

non-DP basis construction Sequential construction: loop on k with Values of in n=3 with LB=2: k=1 k=2 k=3 [0] [0, 1] [0, 2] [1] [2] 20 Basis functions : polynomials in xyz: k=1 k=2 k=3 [0, 0, 0 -2] [0, 1, 0 -1] [0, 2, 0] 1 1 y y 2 1, z, z 2 y, yz y 2 [1, 0] [1, 1] [1, 0, 0 -1] [1, 1, 0] x x xy x, xz xy [2, 0] [2, 0, 0] x 2 x 2 Banff 2016

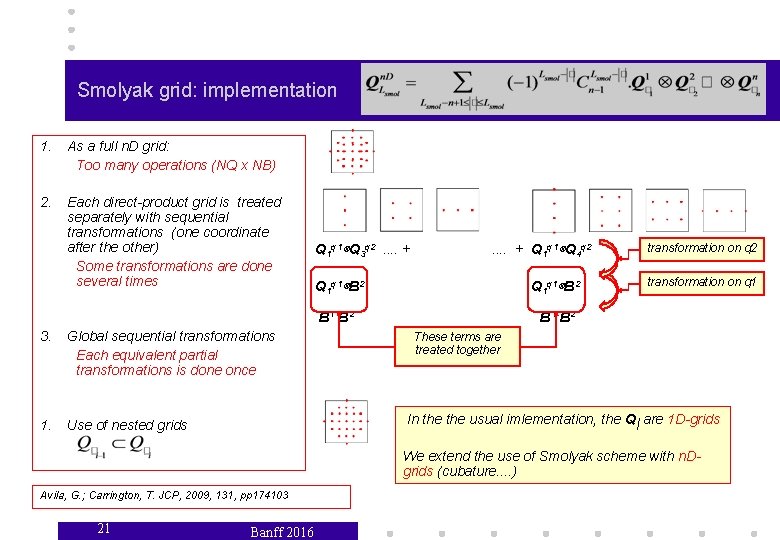
Smolyak grid: implementation 1. As a full n. D grid: Too many operations (NQ x NB) 2. Each direct-product grid is treated separately with sequential transformations (one coordinate after the other) Some transformations are done several times 3. Global sequential transformations Each equivalent partial transformations is done once 1. Use of nested grids Q 1 q 1⊗Q 3 q 2. . . . + Q 1 q 1⊗Q 4 q 2 Q 1 q 1⊗B 2 B 1 B 2 transformation on q 1 These terms are treated together In the usual imlementation, the Ql are 1 D-grids We extend the use of Smolyak scheme with n. Dgrids (cubature. . ) Avila, G. ; Carrington, T. JCP, 2009, 131, pp 174103 21 Banff 2016

Coordinates A fundamental step: A "good" set of coordinates enables to chose a ”compact" basis set and to reduce the computational time and resources. In addition, they have to be adapted to the process: Jacobi coordinates, polyspherical Hyperspherical coordinates Normal modes Valence, z-matrix + other transformations (curvilinear NM, RPH. . . ) 22 Banff 2016

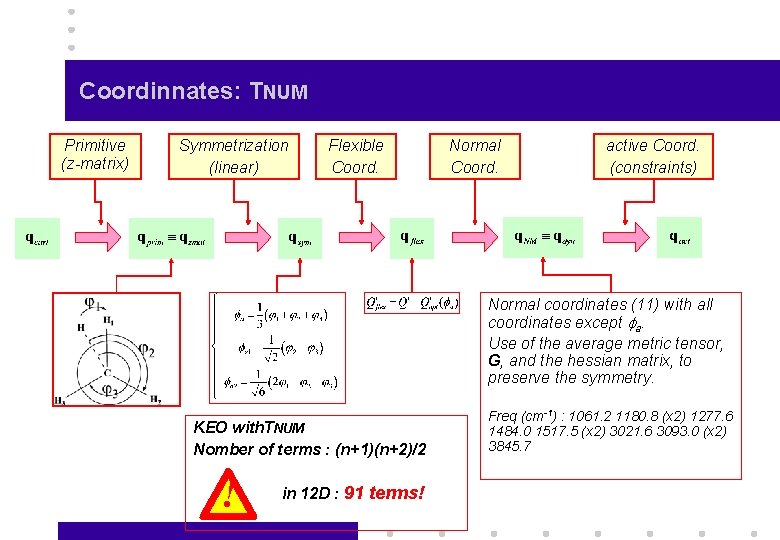
Coordinnates: TNUM Primitive (z-matrix) Symmetrization (linear) Flexible Coord. Normal Coord. active Coord. (constraints) Normal coordinates (11) with all coordinates except fa. Use of the average metric tensor, G, and the hessian matrix, to preserve the symmetry. KEO with. TNUM Nomber of terms : (n+1)(n+2)/2 ! in 12 D : 91 terms! Freq (cm-1) : 1061. 2 1180. 8 (x 2) 1277. 6 1484. 0 1517. 5 (x 2) 3021. 6 3093. 0 (x 2) 3845. 7

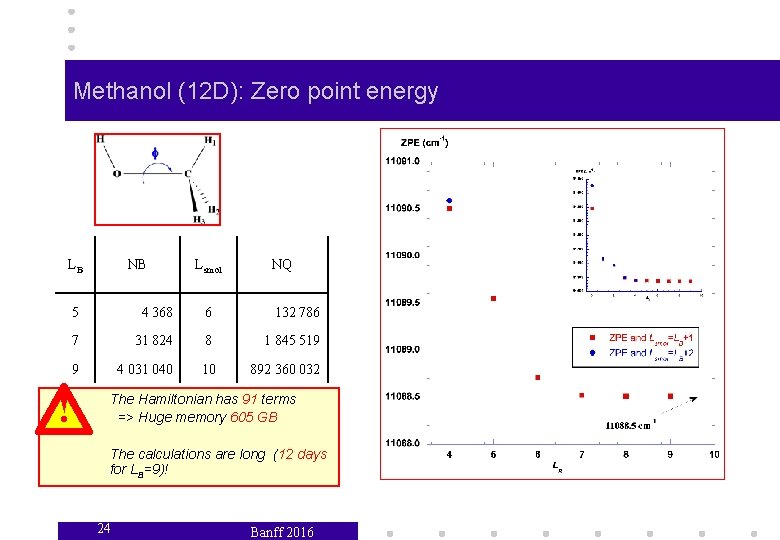
Methanol (12 D): Zero point energy LB ! NB Lsmol NQ 5 4 368 6 132 786 7 31 824 8 1 845 519 9 4 031 040 10 892 360 032 The Hamiltonian has 91 terms => Huge memory 605 GB The calculations are long (12 days for LB=9)! 24 Banff 2016