CSE 245 ComputerAided Circuit Simulation and Verification Spring

CSE 245: Computer-Aided Circuit Simulation and Verification Spring 2006 Chung-Kuan Cheng

Administration • • CK Cheng, CSE 2130, tel. 534 -6184, ckcheng@ucsd. edu Lectures: 9: 30 am ~ 10: 50 am TTH U 413 A 2 Office Hours: 11: 00 am ~ 11: 50 am TTH CSE 2130 Textbooks Electronic Circuit and System Simulation Methods T. L. Pillage, R. A. Rohrer, C. Visweswariah, Mc. Graw-Hill Interconnect Analysis and Synthesis CK Cheng, J. Lillis, S. Lin, N. Chang, John Wiley & Sons • TA: Vincent Peng (hepeng@cs. ucsd. edu), Rui Shi (rshi@cs. ucsd. edu)

Outlines 1. Formulation (2 -3 lectures) 2. Linear System (3 -4 lectures) 3. Matrix Solver (3 -4 lectures) 4. Integration (3 -4 lectures) 5. Non-linear System (2 -3 lectures) 6. Transmission Lines, S Parameters (2 -3 lectures) 7. Sensitivity 8. Mechanical, Thermal, Bio Analysis

Grading • Homeworks and Projects: 60 • Project Presentation: 20% • Final Report: 20%

Motivation • Why – Whole Circuit Analysis, Interconnect Dominance • What – Power, Clock, Interconnect Coupling • Where – Matrix Solvers, Integration Methods – RLC Reduction, Transmission Lines, S Parameters – Parallel Processing – Thermal, Mechanical, Biological Analysis

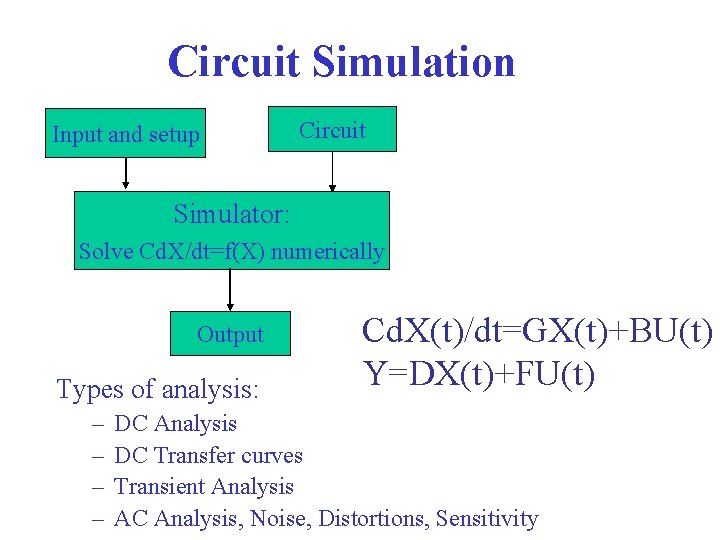
Circuit Simulation Input and setup Circuit Simulator: Solve Cd. X/dt=f(X) numerically Output Types of analysis: – – Cd. X(t)/dt=GX(t)+BU(t) Y=DX(t)+FU(t) DC Analysis DC Transfer curves Transient Analysis AC Analysis, Noise, Distortions, Sensitivity

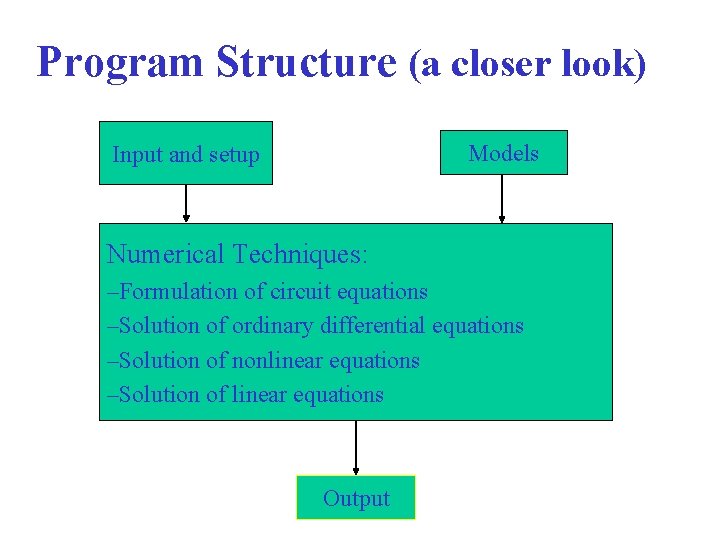
Program Structure (a closer look) Models Input and setup Numerical Techniques: –Formulation of circuit equations –Solution of ordinary differential equations –Solution of nonlinear equations –Solution of linear equations Output

CSE 245: Course Outline • Formulation – – RLC Linear, Nonlinear Components, Transistors, Diodes Incident Matrix Nodal Analysis, Modified Nodal Analysis K Matrix • Linear System – – S domain analysis, Impulse Response Taylor’s expansion Moments, Passivity, Stability, Realizability Symbolic analysis, Y-Delta, BDD analysis • Matrix Solver – LU, KLU, reordering – Mutigrid, PCG, GMRES

CSE 245: Course Outline (Cont’) • Integration – – – Forward Euler, Backward Euler, Trapezoidal Rule Explicit and Implicit Method, Prediction and Correction Equivalent Circuit Errors: Local error, Local Truncation Error, Global Error A-Stable Alternating Direction Implicit Method • Nonlinear System – Newton Raphson, Line Search • Transmission Line, S-Parameter – FDTD: equivalent circuit, convolution – Frequency dependent components • Sensitivity • Mechanical, Thermal, Bio Analysis

Lecture 1: Formulation • KCL/KVL • Sparse Tableau Analysis • Nodal Analysis, Modified Nodal Analysis *some slides borrowed from Berkeley EE 219 Course

Formulation of Circuit Equations • Unknowns – B branch currents (i) – N node voltages (e) – B branch voltages (v) • Equations – N+B Conservation Laws – B Constitutive Equations

Branch Constitutive Equations (BCE) Ideal elements Element Resistor Capacitor Inductor Branch Eqn v = R·i i = C·dv/dt v = L·di/dt Voltage Source Current Source VCVS VCCS CCVS CCCS v = vs, i = ? i = i s, v = ? vs = AV · vc, i = ? is = GT · vc, v = ? vs = RT · ic, i = ? i s = A I · i c, v = ?

Conservation Laws • Determined by the topology of the circuit • Kirchhoff’s Voltage Law (KVL): Every circuit node has a unique voltage with respect to the reference node. The voltage across a branch eb is equal to the difference between the positive and negative referenced voltages of the nodes on which it is incident – No voltage source loop • Kirchhoff’s Current Law (KCL): The algebraic sum of all the currents flowing out of (or into) any circuit node is zero. – No Current Source Cut

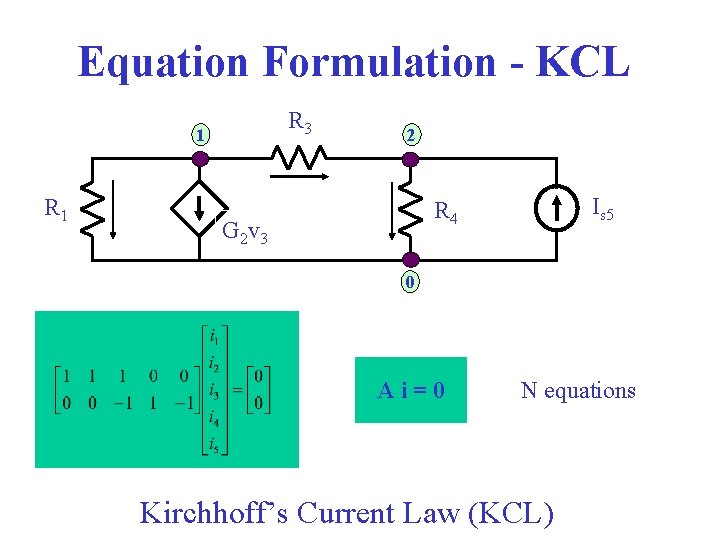
Equation Formulation - KCL R 3 1 R 1 2 Is 5 R 4 G 2 v 3 0 Ai=0 N equations Kirchhoff’s Current Law (KCL)

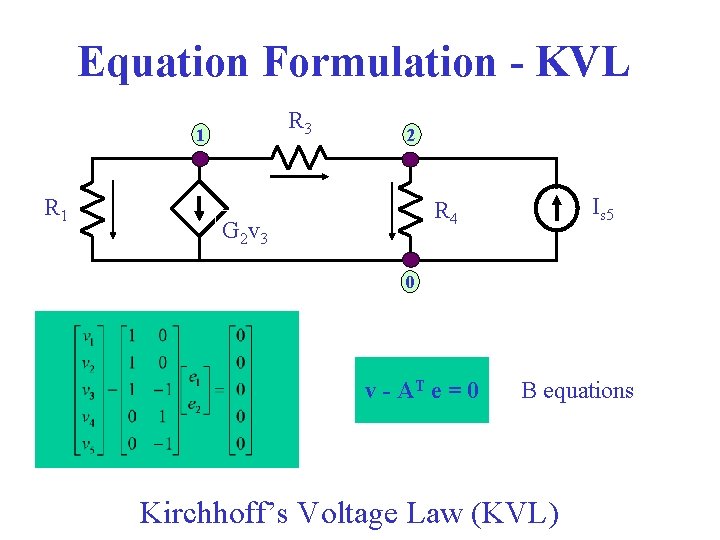
Equation Formulation - KVL R 3 1 R 1 2 Is 5 R 4 G 2 v 3 0 v - AT e = 0 B equations Kirchhoff’s Voltage Law (KVL)

Equation Formulation - BCE R 3 1 R 1 2 R 4 G 2 v 3 Is 5 0 Kvv + i = is B equations

Equation Formulation Node-Branch Incidence Matrix branches n o 1 d 2 e s i 1 2 3 j (+1, -1, 0) N { Aij = +1 if node i is terminal + of branch j -1 if node i is terminal - of branch j 0 if node i is not connected to branch j B

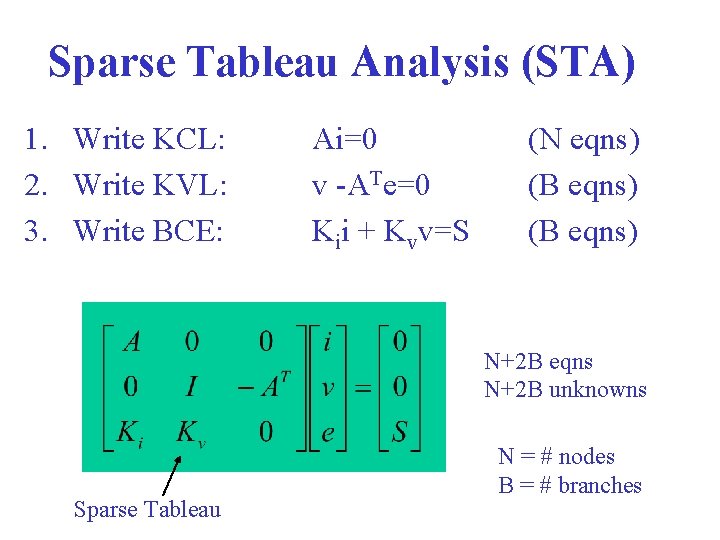
Equation Assembly (Stamping Procedures) • Different ways of combining Conservation Laws and Constitutive Equations – Sparse Table Analysis (STA) – Modified Nodal Analysis (MNA)

Sparse Tableau Analysis (STA) 1. Write KCL: 2. Write KVL: 3. Write BCE: Ai=0 v -ATe=0 Kii + Kvv=S (N eqns) (B eqns) N+2 B eqns N+2 B unknowns Sparse Tableau N = # nodes B = # branches

Sparse Tableau Analysis (STA) Advantages • It can be applied to any circuit • Eqns can be assembled directly from input data • Coefficient Matrix is very sparse Problem Sophisticated programming techniques and data structures are required for time and memory efficiency

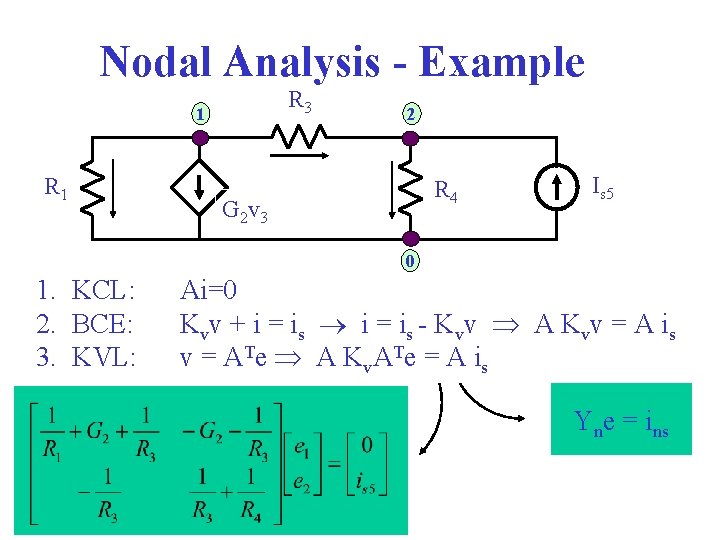
Nodal Analysis (NA) 1. Write KCL A·i=0 (N eqns, B unknowns) 2. Use BCE to relate branch currents to branch voltages i=f(v) (B unknowns B unknowns) 3. Use KVL to relate branch voltages to node voltages 4. v=h(e) (B unknowns N unknowns) Yne=ins Nodal Matrix N eqns N unknowns N = # nodes

Nodal Analysis - Example R 3 1 R 1 2 R 4 G 2 v 3 Is 5 0 1. KCL: 2. BCE: 3. KVL: Ai=0 Kvv + i = is - Kvv A Kvv = A is v = ATe A Kv. ATe = A is Yne = ins

Nodal Analysis • Example shows NA may be derived from STA • Better: Yn may be obtained by direct inspection (stamping procedure) – Each element has an associated stamp – Yn is the composition of all the elements’ stamps

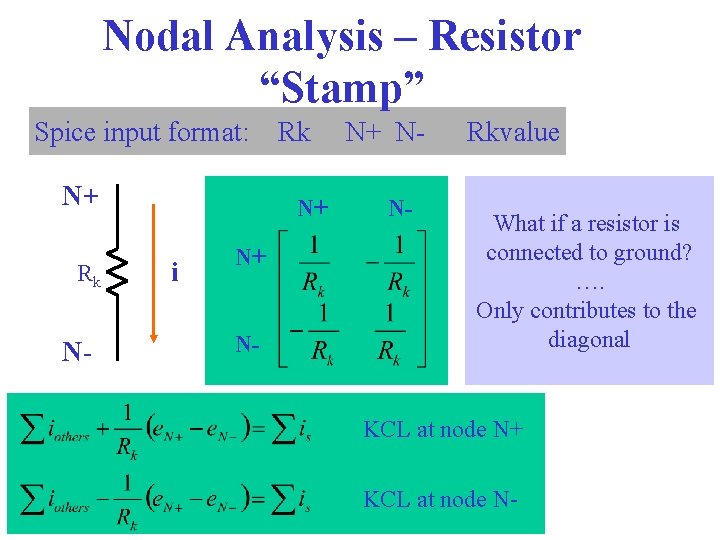
Nodal Analysis – Resistor “Stamp” Spice input format: N+ Rk N- Rk N+ i N+ N- N+ NN- Rkvalue What if a resistor is connected to ground? …. Only contributes to the diagonal KCL at node N+ KCL at node N-

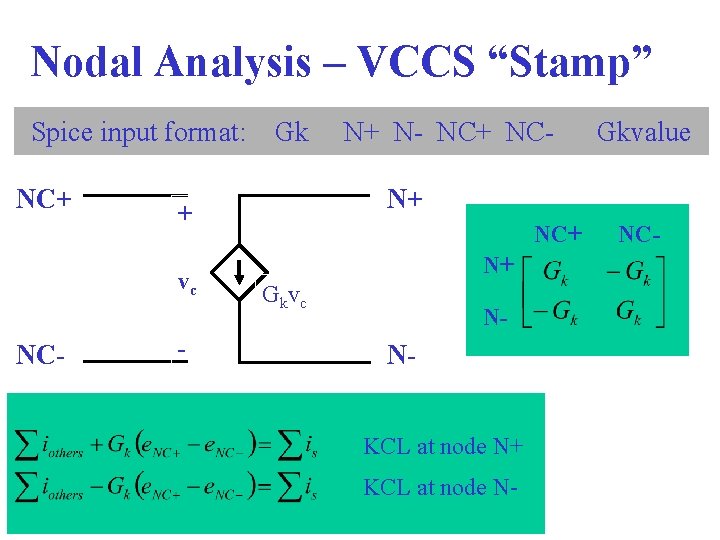
Nodal Analysis – VCCS “Stamp” Spice input format: NC+ - N+ N- NC+ NC- Gkvalue N+ + vc NC- Gk NC+ N+ Gkvc N- NKCL at node N+ KCL at node N- NC-

Nodal Analysis – Current source “Stamp” Spice input format: Ik N+ N+ NN+ Ik N- N- N+ N- Ikvalue

Nodal Analysis (NA) Advantages • Yn is often diagonally dominant and symmetric • Eqns can be assembled directly from input data • Yn has non-zero diagonal entries • Yn is sparse (not as sparse as STA) and smaller than STA: Nx. N compared to (N+2 B)x(N+2 B) Limitations • Conserved quantity must be a function of node variable – Cannot handle floating voltage sources, VCVS, CCCS, CCVS

Modified Nodal Analysis (MNA) How do we deal with independent voltage sources? + Ekl l k ikl k l • ikl cannot be explicitly expressed in terms of node voltages it has to be added as unknown (new column) • ek and el are not independent variables anymore a constraint has to be added (new row)

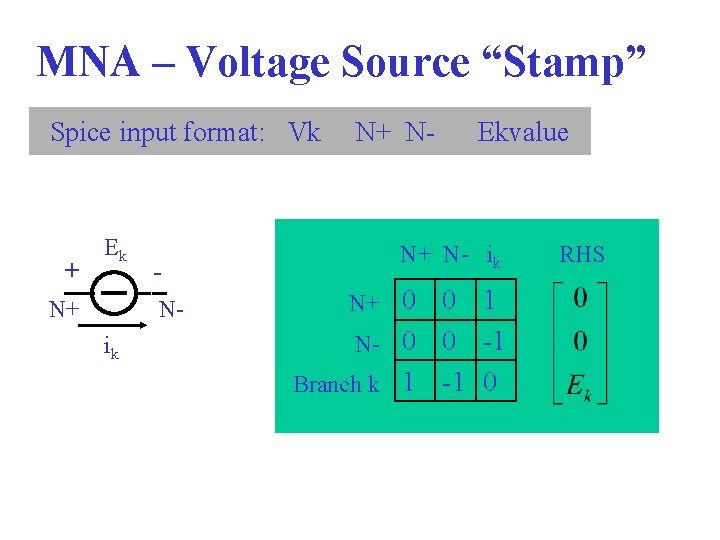
MNA – Voltage Source “Stamp” Spice input format: Vk + Ek N+ N- ik N+ N- Ekvalue N+ N- ik N+ 0 0 1 N- 0 0 -1 Branch k 1 -1 0 RHS

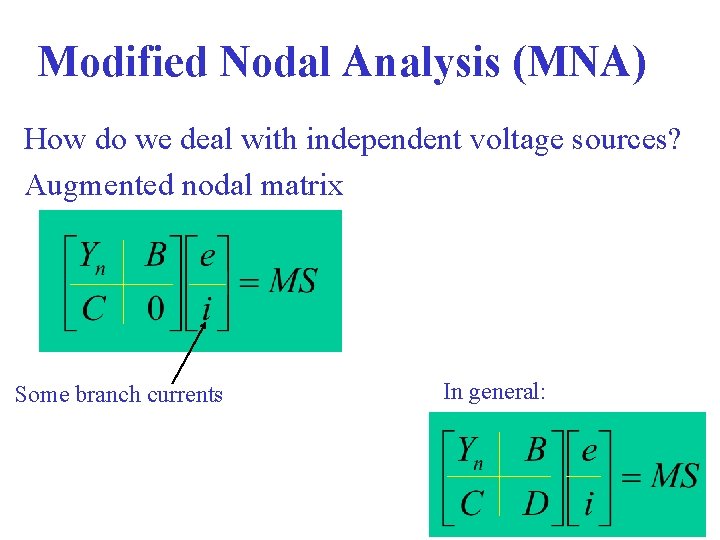
Modified Nodal Analysis (MNA) How do we deal with independent voltage sources? Augmented nodal matrix Some branch currents In general:

MNA – General rules • A branch current is always introduced as and additional variable for a voltage source or an inductor • For current sources, resistors, conductors and capacitors, the branch current is introduced only if: – Any circuit element depends on that branch current – That branch current is requested as output

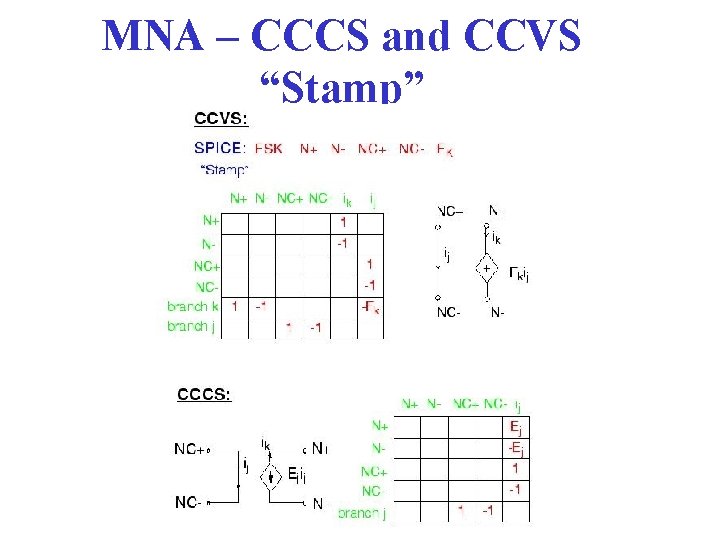
MNA – CCCS and CCVS “Stamp”

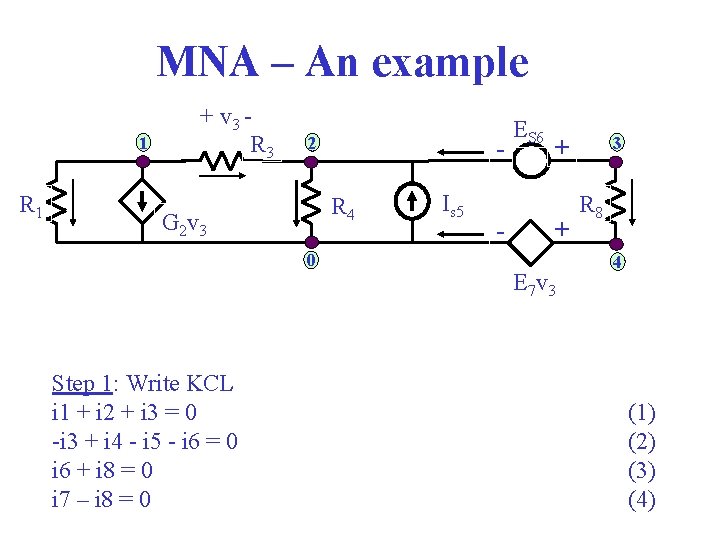
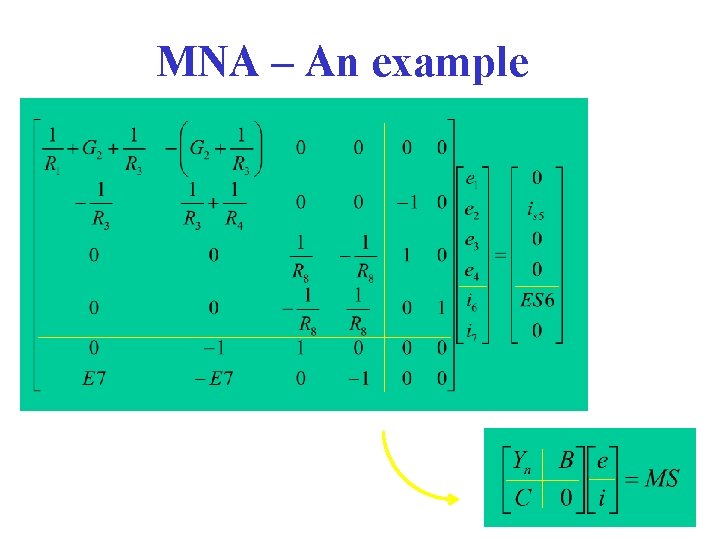
MNA – An example 1 R 1 + v 3 R 3 2 R 4 G 2 v 3 0 Step 1: Write KCL i 1 + i 2 + i 3 = 0 -i 3 + i 4 - i 5 - i 6 = 0 i 6 + i 8 = 0 i 7 – i 8 = 0 Is 5 - ES 6 3 + + E 7 v 3 R 8 4 (1) (2) (3) (4)

MNA – An example Step 2: Use branch equations to eliminate as many branch currents as possible 1/R 1·v 1 + G 2 ·v 3 + 1/R 3·v 3 = 0 (1) - 1/R 3·v 3 + 1/R 4·v 4 - i 6 = is 5 (2) i 6 + 1/R 8·v 8 = 0 (3) i 7 – 1/R 8·v 8 = 0 (4) Step 3: Write down unused branch equations v 6 = ES 6 v 7 – E 7·v 3 = 0 (b 7) (b 6)

MNA – An example Step 4: Use KVL to eliminate branch voltages from previous equations 1/R 1·e 1 + G 2·(e 1 -e 2) + 1/R 3·(e 1 -e 2) = 0 (1) - 1/R 3·(e 1 -e 2) + 1/R 4·e 2 - i 6 = is 5 (2) i 6 + 1/R 8·(e 3 -e 4) = 0 (3) i 7 – 1/R 8·(e 3 -e 4) = 0 (4) (e 3 -e 2) = ES 6 (b 6) e 4 – E 7·(e 1 -e 2) = 0 (b 7)

MNA – An example

Modified Nodal Analysis (MNA) Advantages • MNA can be applied to any circuit • Eqns can be assembled directly from input data • MNA matrix is close to Yn Limitations • Sometimes we have zeros on the main diagonal