3 V Projection 3 V 1 Orthogonal Projection



















- Slides: 20

3. V. Projection 3. V. 1. Orthogonal Projection Into a Line 3. V. 2. Gram-Schmidt Orthogonalization 3. V. 3. Projection Into a Subspace 3. V. 1. & 2. deal only with inner product spaces. 3. V. 3 is applicable to any direct sum space.

3. V. 1. Orthogonal Projection Into a Line Definition 1. 1: Orthogonal Projection The orthogonal projection of v into the line spanned by a nonzero s is the vector. Example 1. 3: Orthogonal projection of the vector ( 2 3 )T into the line y = 2 x.

Example 1. 4: Orthogonal projection of a general vector in R 3 into the y-axis Example 1. 5: Project = Discard orthogonal components A railroad car left on an east-west track without its brake is pushed by a wind blowing toward the northeast at fifteen miles per hour; what speed will the car reach?

Example 1. 6: Nearest Point A submarine is tracking a ship moving along the line y = 3 x + 2. Torpedo range is one-half mile. Can the sub stay where it is, at the origin on the chart, or must it move to reach a place where the ship will pass within range? Ship’s path is parallel to vector Point p of closest approach is (Out of range)

Exercises 3. V. 1. 1. Consider the function mapping a plane to itself that takes a vector to its projection into the line y = x. (a) Produce a matrix that describes the function’s action. (b) Show also that this map can be obtained by first rotating everything in the plane π/4 radians clockwise, then projecting into the x-axis, and then rotating π/4 radians counterclockwise.

3. V. 2. Gram-Schmidt Orthogonalization Given a vector s, any vector v in an inner product space can be decomposed as where Definition 2. 1: Mutually Orthogonal Vectors v 1, …, vk Rn are mutually orthogonal if vi · vj = 0 i j Theorem 2. 2: A set of mutually orthogonal non-zero vectors is linearly independent. Proof: → → cj = 0 j Corollary 2. 3: A set of k mutually orthogonal nonzero vectors in V k is a basis for the space. Definition 2. 5: Orthogonal Basis An orthogonal basis for a vector space is a basis of mutually orthogonal vectors.

Example 2. 6: Turn into an orthogonal basis for R 3.

Theorem 2. 7: Gram-Schmidt Orthogonalization If β 1 , …, βk is a basis for a subspace of Rn the κj s calculated from the following scheme is an orthogonal basis for the same subspace. Proof: Then For m 2 , Let β 1 , …, βm be mutually orthogonal, and QED

If each κj is furthermore normalized, the basis is called orthonormal. The Gram-Schmidt scheme simplifies to:

Exercises 3. V. 2. 1. Perform the Gram-Schmidt process on this basis for R 3, 2. Show that the columns of an n n matrix form an orthonormal set if and only if the inverse of the matrix is its transpose. Produce such a matrix.

3. V. 3. Projection Into a Subspace Definition 3. 1: For any direct sum V = M N and any v V such that v=m+n with m M and n N The projection of v into M along N is defined as proj. M, N (v) = m Reminder: • M & N need not be orthogonal. • There need not even be an inner product defined.

Example 3. 2: The space M 2 2 of 2 2 matrices is the direct sum of Task: Find proj. M , N (A), where Solution: Let the bases for M & N be → ∴ is a basis for M 2 2.

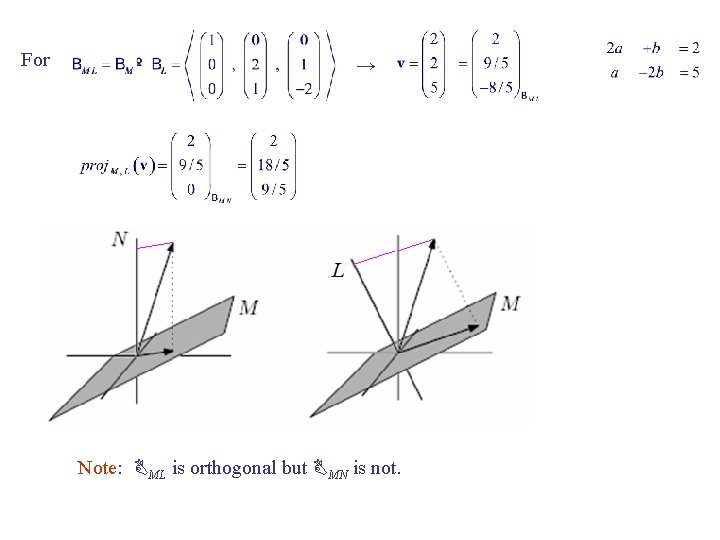
Example 3. 3: Both subscripts on proj. M , N (v) are significant. Consider with basis and subspaces & It’s straightforward to verify Task: Find proj. M , N (v) and proj. M , L (v) where Solution: For →

For → Note: BML is orthogonal but BMN is not.

Definition 3. 4: Orthogonal Complement The orthogonal complement of a subspace M of Rn is M = { v Rn | v is perpendicular to all vectors in M } ( read “M perp” ). The orthogonal projection proj. M (v ) of a vector is its projection into M along M . Example 3. 5: In R 3, find the orthogonal complement of the plane Solution: → Natural basis for P is ( parameter = z)

Lemma 3. 7: Let M be a subspace of Rn. Hence, v Rn, Then M is also a subspace and Rn = M M . v proj. M (v) is perpendicular to all vectors in M. Proof: Construct bases using G-S orthogonalization. Theorem 3. 8: Let v be a vector in Rn and let M be a subspace of Rn with basis β 1 , …, βk . If A is the matrix whose columns are the β’s then proj. M (v ) = c 1β 1 + …+ ck βk where the coefficients ci are the entries of the vector (AT A) AT v. That is, proj. M (v ) = A (AT A) 1 AT v. Proof: By lemma 3. 7, where c is a column vector → → →

Interpretation of Theorem 3. 8: If B = β 1 , …, βk is an orthonormal basis, then ATA = I. In which case, proj. M (v ) = A (AT A) 1 AT v = A AT v. with In particular, if B = Ek , then A = AT = I. In case B is not orthonormal, the task is to find C s. t. B = AC and BTB = I. → Hence →

Example 3. 9: To orthogonally project From → into subspace we get

Exercises 3. V. 3. 1. Project v into M along N, where 2. Find M for

3. Define a projection to be a linear transformation t : V → V with the property that repeating the projection does nothing more than does the projection alone: ( t t )(v) = t (v) for all v V. (a) Show that for any such t there is a basis B = β 1 , …, βn for V such that where r is the rank of t. (b) Conclude that every projection has a block partial-identity representation:
 Orthogonal projection in computer graphics
Orthogonal projection in computer graphics Orthogonal projection
Orthogonal projection Cavalier axonometric
Cavalier axonometric Scalar projection vs vector projection
Scalar projection vs vector projection Isometric
Isometric Third and first angle projection
Third and first angle projection First angle projection and third angle projection
First angle projection and third angle projection Properties of an orthogonal matrix
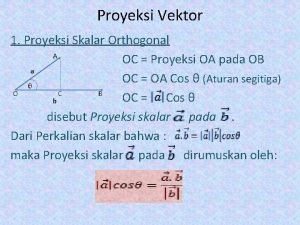
Properties of an orthogonal matrix Materi proyeksi skalar ortogonal
Materi proyeksi skalar ortogonal Irange tree
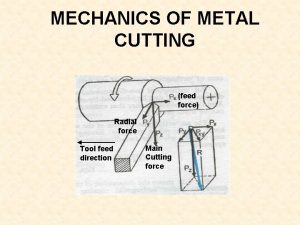
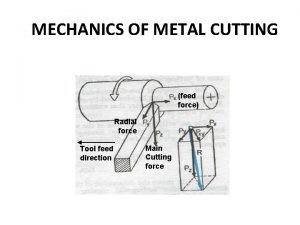
Irange tree Feed force in orthogonal cutting
Feed force in orthogonal cutting Example of an orthogonal matrix
Example of an orthogonal matrix Merchant circle diagram
Merchant circle diagram Orthogonal matrix
Orthogonal matrix Fourier series and orthogonal functions
Fourier series and orthogonal functions Orthnormal
Orthnormal Orthogonal basis
Orthogonal basis Theory of metal cutting
Theory of metal cutting Orthogonal transformation matrix
Orthogonal transformation matrix 2d orthogonal and unitary transforms
2d orthogonal and unitary transforms Orthogonal
Orthogonal