3 Laguerre Functions Laguerre ODE Rodrigues Formula Schlaefli






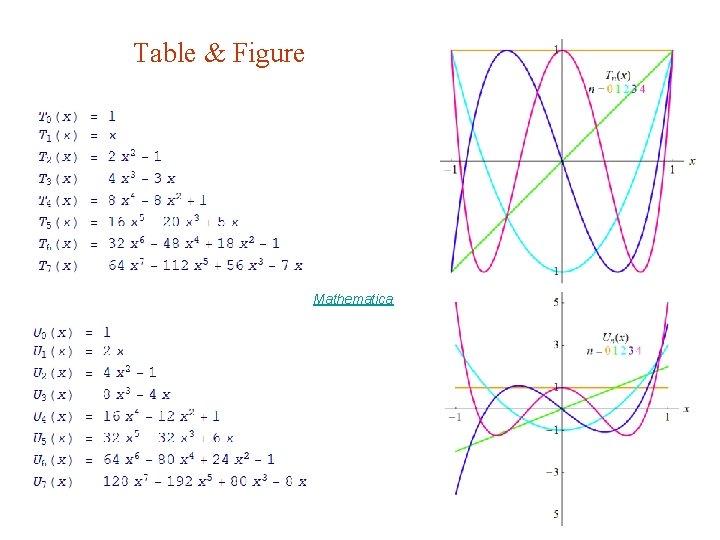
![Table & Figure. Laguerre Polynomials Ln orthogonal over [0, ] Mathematica Table & Figure. Laguerre Polynomials Ln orthogonal over [0, ] Mathematica](https://slidetodoc.com/presentation_image_h/9bcfe443fd0564d34dfb76983a7d47a3/image-7.jpg)























- Slides: 34

3. Laguerre Functions Laguerre ODE Rodrigues Formula : Schlaefli integral : Hermitian form Laguerre Polynomials ( n! changes scale ) C encircles x but no other singularities

Generating Function

Properties of Ln(x)



Eliminate g as before
![Table Figure Laguerre Polynomials Ln orthogonal over 0 Mathematica Table & Figure. Laguerre Polynomials Ln orthogonal over [0, ] Mathematica](https://slidetodoc.com/presentation_image_h/9bcfe443fd0564d34dfb76983a7d47a3/image-7.jpg)
Table & Figure. Laguerre Polynomials Ln orthogonal over [0, ] Mathematica

Power Series

Orthonormality orthogonality Ex. 18. 3. 3 Set

Associated Laguerre Polynomials Alternative definition:

Generating Function Gives Lnk with k 0 only. i. e. , only terms n l are used. Proof : (1+t) both sides :

gl is a correct generating function for Lnk. gl has correct scale.

same as before

More Recurrence

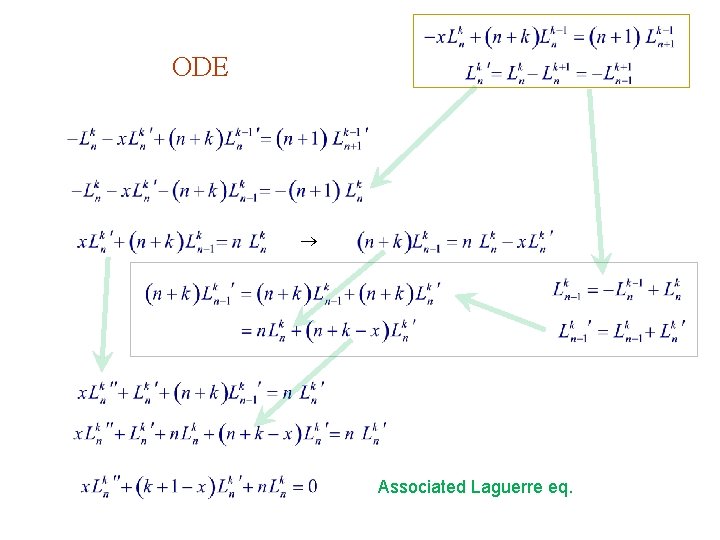
ODE Associated Laguerre eq.

Hermitian form Orthogonality obtained from

Rodrigues formula (re-scaled by n!) Set Laguerre functions Set Mathematica For non-integer n, solutions to ODE are not polynomials & diverge as x k ex.

Example 18. 3. 1. The Hydrogen Atom Schrodinger eq. for H-like atom of atomic number Z. SI units B. C. for bound states : Let R(0) finite & R( ) = 0.

Let with

1 must be an integer. Integers Set Bohr radius

4. Chebyshev Polynomials Ultraspherical polynomials (Gegenbauer polynomials) = ½ Legendre polynomials = 0 (1) Type I (II) Chebyshev (Tchebycheff / Tschebyschow ) polynomials Type II Polynomials Un : Application: 4 -D spherical harmonics in angular momentum theory.

Type I Polynomials Tn (x) = 0 : LHS = 1. Remedy: = 0 : where Set

Recurrence Similarly

Other recurrence :

Table & Figure Mathematica

ODEs unuable Better choice is Proof : Rodrigues formula cn( ) = scaling constant

Special Values Ex. 18. 4. 1 -2 Rodrigues formula 0 1

Trigonometric Form



From g( ) or ODE (Frobenius series) :

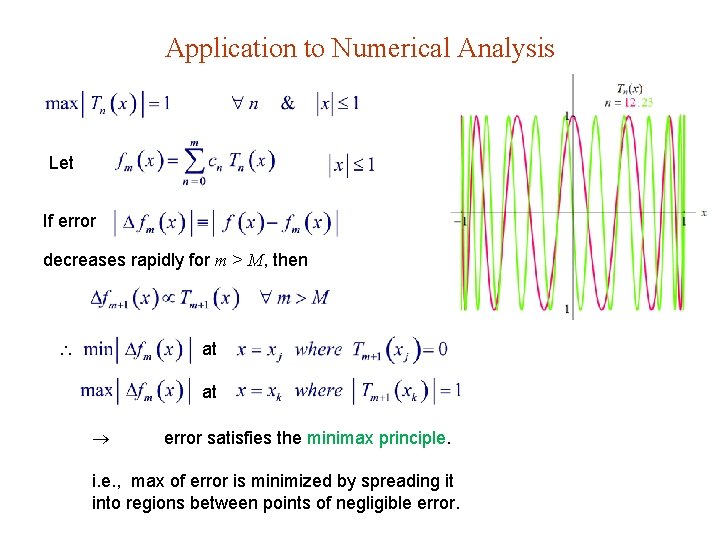
Application to Numerical Analysis Let If error decreases rapidly for m > M, then at at error satisfies the minimax principle. i. e. , max of error is minimized by spreading it into regions between points of negligible error.

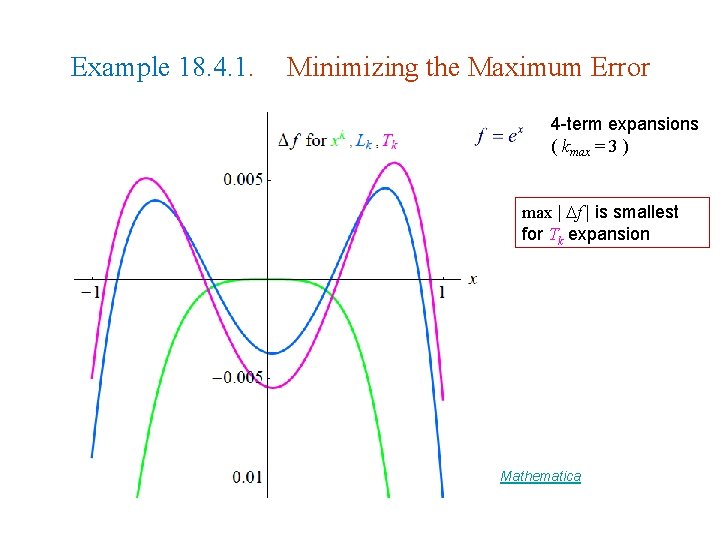
Example 18. 4. 1. Minimizing the Maximum Error 4 -term expansions ( kmax = 3 ) max | f | is smallest for Tk expansion Mathematica

Orthogonality 0 : 1 : Normalization obtained using trigonometric form
 Schlaefli integral
Schlaefli integral Bessel
Bessel Legendre duplication formula proof
Legendre duplication formula proof 29400x3
29400x3 Rodrigues' rotation formula
Rodrigues' rotation formula Maniobra laguerre
Maniobra laguerre Edmond laguerre
Edmond laguerre Legendre polynomials orthogonality
Legendre polynomials orthogonality Tumulo de amalia rodrigues
Tumulo de amalia rodrigues Python rodrigues
Python rodrigues Desmond blackburn
Desmond blackburn Ubirajara pereira rodrigues filho
Ubirajara pereira rodrigues filho Monologo nelson rodrigues
Monologo nelson rodrigues Nadir afonso rodrigues
Nadir afonso rodrigues Amanestic
Amanestic Dr natercia rodrigues
Dr natercia rodrigues Antonio rodrigues de freitas junior
Antonio rodrigues de freitas junior Nerival rodrigues festa junina
Nerival rodrigues festa junina Faculdade almeida rodrigues
Faculdade almeida rodrigues Amlia rodrigues
Amlia rodrigues Maria emília ufg
Maria emília ufg John paul rodrigues
John paul rodrigues Camila rodrigues roberto costa
Camila rodrigues roberto costa Babak omidi
Babak omidi Luana ferri
Luana ferri Simon rodrigues and associates
Simon rodrigues and associates Piecewise functions absolute value
Piecewise functions absolute value How to evaluate function
How to evaluate function Evaluating functions and operations on functions
Evaluating functions and operations on functions Syntax examples
Syntax examples Dirge examples
Dirge examples Singular solution of ode
Singular solution of ode Poems with personification similes and metaphors
Poems with personification similes and metaphors Oskar maarleveld
Oskar maarleveld Que es un ode
Que es un ode