296 3 Algorithms in the Real World Linear

296. 3: Algorithms in the Real World Linear and Integer Programming II – Ellipsoid algorithm – Interior point methods 296. 3 1

Ellipsoid Algorithm First known-to-be polynomial-time algorithm for linear programming (Khachian 79) Solves find x subject to Ax ≤ b i. e. , find a feasible solution Run Time: O(n 4 L), where L = #bits to represent A and b Problem in practice: always takes this much time. 296. 3 2

Reduction from general case To solve: maximize: z = c. Tx subject to: Ax ≤ b, x≥ 0 Convert to: find: x, y subject to: Ax ≤ b, -x ≤ 0 -ATy ≤ –c -y ≤ 0 -c. Tx +y. Tb ≤ 0 296. 3 Could add constraint -c. Tx ≤ -z 0, do binary search over various values of z 0 to find feasible solution with maximum z, but approach based on dual gives direct solution. 3

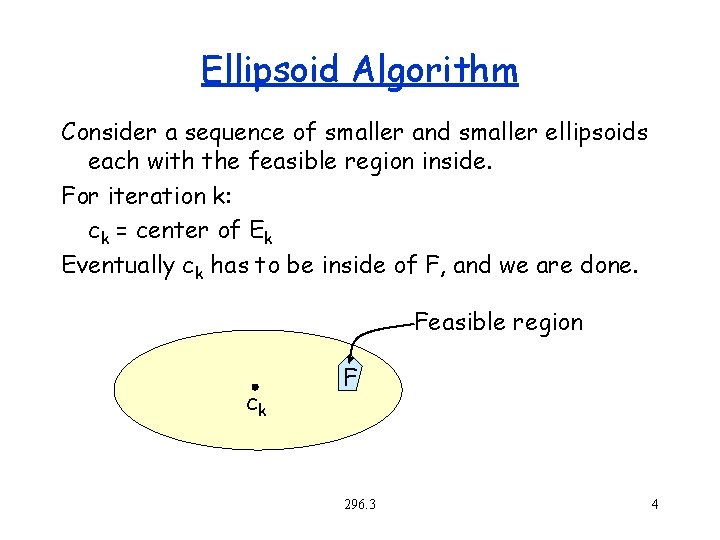
Ellipsoid Algorithm Consider a sequence of smaller and smaller ellipsoids each with the feasible region inside. For iteration k: ck = center of Ek Eventually ck has to be inside of F, and we are done. Feasible region ck F 296. 3 4

Ellipsoid Algorithm To find the next smaller ellipsoid: find most violated constraint ak find smallest ellipsoid that includes constraint Feasible region ck F ak 296. 3 5

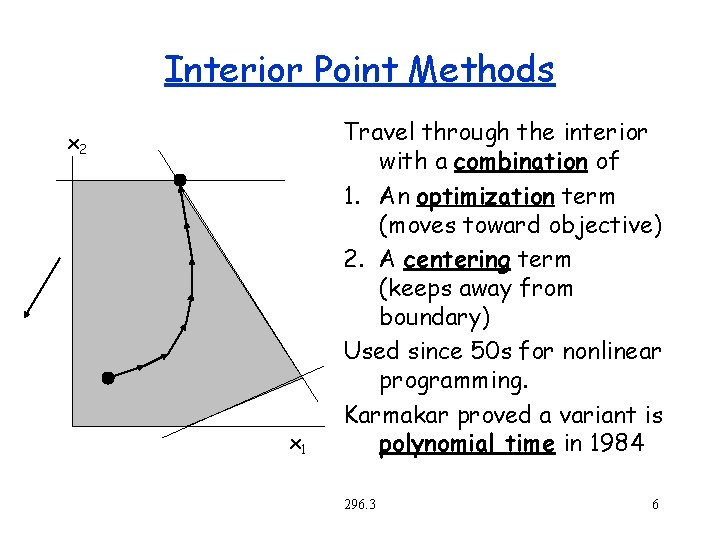
Interior Point Methods x 2 x 1 Travel through the interior with a combination of 1. An optimization term (moves toward objective) 2. A centering term (keeps away from boundary) Used since 50 s for nonlinear programming. Karmakar proved a variant is polynomial time in 1984 296. 3 6

Methods Affine scaling: simplest, but no known time bounds Potential reduction: O(n. L) iterations Central trajectory: O(n 1/2 L) iterations The time for each iteration involves solving a linear system so it takes polynomial time. The “real world” time depends heavily on the matrix structure. 296. 3 7

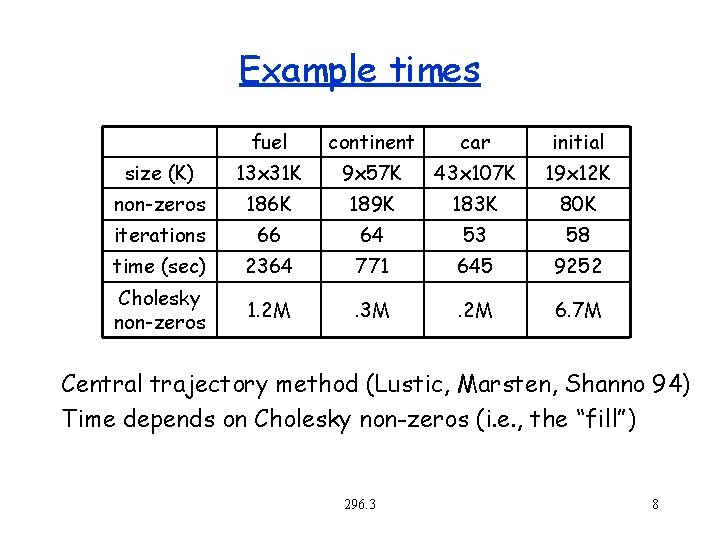
Example times fuel continent car initial size (K) 13 x 31 K 9 x 57 K 43 x 107 K 19 x 12 K non-zeros 186 K 189 K 183 K 80 K iterations 66 64 53 58 time (sec) 2364 771 645 9252 Cholesky non-zeros 1. 2 M . 3 M . 2 M 6. 7 M Central trajectory method (Lustic, Marsten, Shanno 94) Time depends on Cholesky non-zeros (i. e. , the “fill”) 296. 3 8

Assumptions We are trying to solve the problem: minimize z = c. Tx subject to Ax = b x≥ 0 296. 3 9

Outline 1. 2. 3. 4. 5. 6. 7. Centering Methods Overview Picking a direction to move toward the optimal Staying on the Ax = b hyperplane (projection) General method Example: Affine scaling Example: potential reduction Example: log barrier 296. 3 10

Centering: option 1 The “analytical center”: Minimize: y = -Si=1 n lg xi y goes to infinity as x approaches any boundary. x 5 x 1 x 2 x 4 x 3 296. 3 11

Centering: option 2 Elliptical Scaling: (c 1, c 2) Dikin Ellipsoid The idea is to bias spaced based on the ellipsoid. More on this later. 296. 3 12

Finding the Optimal solution Let’s say f(x) is the combination of the “centering term” c(x) and the “optimization term” z(x) = c. T x. We would like this to have the same minimum over the feasible region as z(x) but can otherwise be quite different. In particular c(x) and hence f(x) need not be linear. Goal: find the minimum of f(x) over the feasible region starting at some interior point x 0 Can do this by taking a sequence of steps toward the minimum. How do we pick a direction for a step? 296. 3 13

Picking a direction: steepest descent Option 1: Find the steepest descent on x at x 0 by taking the gradient: Problem: the gradient might be changing rapidly, so local steepest descent might not give us a good direction. Any ideas for better selection of a direction? 296. 3 14

Picking a direction: Newton’s method Consider the truncated Taylor series: To find the minimum of f(x) take the derivative and set to 0. In matrix form, for arbitrary dimension: Hessian 296. 3 15

Next Step? Now that we have a direction, what do we do? 296. 3 16

Remaining on the support plane Constraint: Ax = b A is a n x (n + m) matrix. The equation describes an m dimensional hyperplane in a n+m dimensional space. The hyperplane basis is the null space of A A = defines the “slope” b = defines an “offset” x 2 x 1 + 2 x 2 = 4 x 1 + 2 x 2 = 3 3 296. 3 4 x 1 17

Projection Need to project our direction onto the plane defined by the null space of A. We want to calculate Pc 296. 3 18

Calculating Pc Pc = (I – AT(AAT)-1 A)c = c – ATw where ATw = AT(AAT)-1 Ac giving AATw = AAT(AAT)-1 Ac = Ac so all we need to do is solve for w in: AATw = Ac This can be solved with a sparse solver as described in the graph separator lectures. This is the workhorse of the interior-point methods. Note that AAT will be more dense than A. 296. 3 19

Next step? We now have a direction c and its projection d onto the constraint plane defined by Ax = b. What do we do now? To decide how far to go we can find the minimum of f(x) along the line defined by d. Not too hard if f(x) is reasonably nice (e. g. , has one minimum along the line). Alternatively we can go some fraction of the way to the boundary (e. g. , 90%) 296. 3 20

General Interior Point Method Pick start x 0 Factor AAT (i. e. , find LU decomposition) Repeat until done (within some threshold) – decide on function to optimize f(x) (might be the same for all iterations) – select direction d based on f(x) (e. g. , with Newton’s method) – project d onto null space of A (using factored AAT and solving a linear system) – decide how far to go along that direction Caveat: every method is slightly different 296. 3 21

Affine Scaling Method A biased steepest descent. On each iteration solve: minimize c Ty subject to Ay = 0 y. TD-2 y ≤ 1 Dikin ellipsoid Note that: 1. Ellipsoid is centered around current solution x 2. y is in the null space of A and can therefore be used as the direction d without projection 3. we are optimizing in the desired direction c. T What does the Dikin Ellipsoid do for us? 296. 3 22

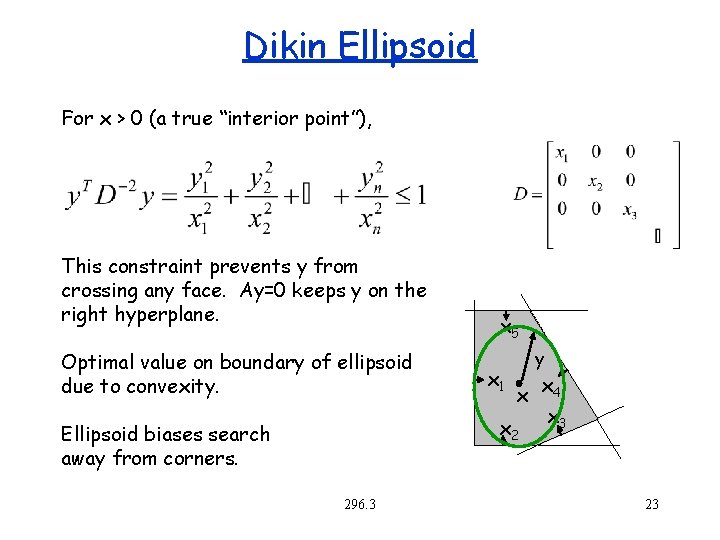
Dikin Ellipsoid For x > 0 (a true “interior point”), This constraint prevents y from crossing any face. Ay=0 keeps y on the right hyperplane. Optimal value on boundary of ellipsoid due to convexity. x 5 x 1 y x x 4 x 3 x 2 Ellipsoid biases search away from corners. 296. 3 23

Finding Optimal minimize c. Ty subject to Ay = 0 y. TD-2 y ≤ 1 But this looks harder to solve than a linear program! We now have a non-linear constraint y. TD-2 y ≤ 1. Symmetry and lack of corners actually makes this easier to solve. 296. 3 24

How to compute By substitution of variables: y = Dy’ minimize: c. TDy’ subject to: ADy’ = 0 y’TDD-2 Dy’ ≤ 1 y’Ty’ ≤ 1 The sphere y’Ty’ ≤ 1 is unbiased. So we project the direction c. TD = Dc onto the nullspace of B = AD: y’ = (I – BT(BBT)-1 B)Dc and y = Dy’ = D (I – BT(BBT)-1 B)Dc As before, solve for w in BBTw = BDc and y = D(Dc – BTw) = D 2(c – ATw) 296. 3 25

Affine Interior Point Method Pick start x 0 Symbolically factor AAT Repeat until done (within some threshold) – B = ADi – Solve BBTw = ADDTAT = BDc for w (use symbolically factored AAT… same non-zero structure) – d = Di(Dic – BTw) – move in direction d a fraction a of the way to the boundary (something like a =. 96 is used in practice) Note that Di changes on each iteration since it depends on x i 296. 3 26

Potential Reduction Method minimize: z = q ln(c. Tx – b. Ty) - Sj=1 n ln(xj) subject to: Ax = b x≥ 0 y. A + s = 0 (dual problem) s≥ 0 First term of z is the optimization term The second term of z is the centering term. The objective function is not linear. Use hill climbing or “Newton Step” to optimize. (c. Tx – b. Ty) goes to 0 near the solution 296. 3 27

Central Trajectory (log barrier) Dates back to 50 s for nonlinear problems. On step i: 1. minimize: c. Tx - mk åj=1 n ln(xj), s. t. Ax = b, x > 0 2. select: mk+1 ≤ mk Each minimization can be done with a constrained Newton step. mk needs to approach zero to terminate. A primal-dual version using higher order approximations is currently the best interiorpoint method in practice. 296. 3 28

Summary of Algorithms 1. Actual algorithms used in practice are very sophisticated 2. Practice matches theory reasonably well 3. Interior-point methods dominate when A. Large n B. Small Cholesky factors (i. e. , low fill) C. Highly degenerate 4. Simplex dominates when starting from a previous solution very close to the final solution 5. Ellipsoid algorithm not currently practical 6. Large problems can take hours or days to solve. Parallelism is very important. 296. 3 29