2 Analyzing TwoVariable Data Lesson 2 3 Correlation

2 Analyzing Two-Variable Data Lesson 2. 3 Correlation Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Correlation Learning Targets After this lesson, you should be able to: ü Estimate the correlation between two quantitative variables from a scatterplot. ü Interpret the correlation. ü Distinguish correlation from causation. Statistics and Probability with Applications, 3 rd Edition 2

Correlation In the previous lesson, we used direction, form, and strength to describe the association between two quantitative variables. To quantify the strength of a linear relationship between two quantitative variables, we use the correlation r. Correlation r The correlation r is a measure of the strength and direction of a linear relationship between two quantitative variables. • The correlation r falls between – 1 and 1 (– 1 ≤ r ≤ 1). • If the relationship is negative, then r < 0. If the relationship is positive, then r > 0. • If r = 1 or r = – 1, then there is a perfect linear relationship. In other words, all of the points will be exactly on a line. • If there is very little scatter from the linear form, then r is close to 1 or – 1. The more scatter from the linear form, the closer r is to 0. Statistics and Probability with Applications, 3 rd Edition 3
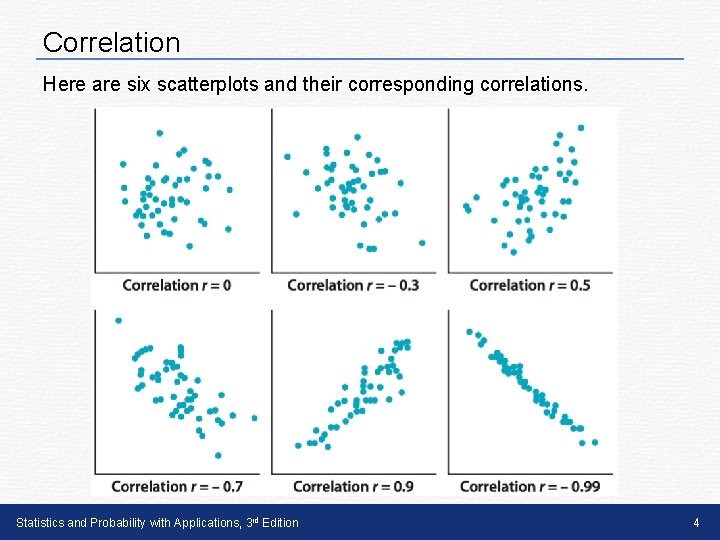
Correlation Here are six scatterplots and their corresponding correlations. Statistics and Probability with Applications, 3 rd Edition 4
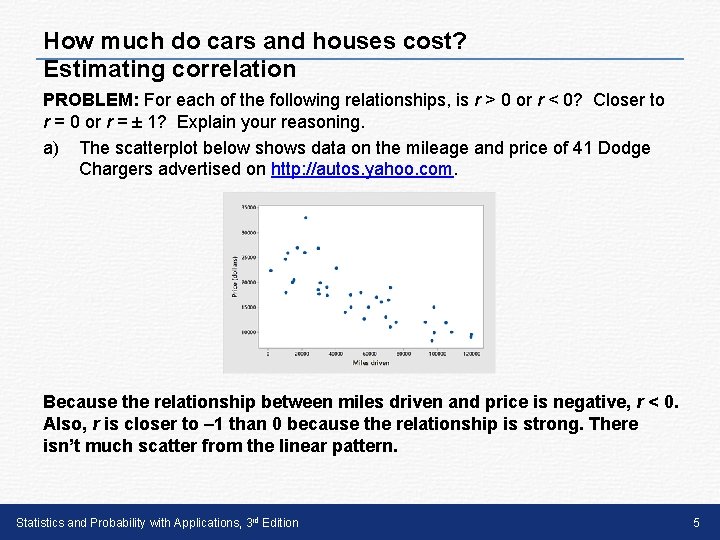
How much do cars and houses cost? Estimating correlation PROBLEM: For each of the following relationships, is r > 0 or r < 0? Closer to r = 0 or r = ± 1? Explain your reasoning. a) The scatterplot below shows data on the mileage and price of 41 Dodge Chargers advertised on http: //autos. yahoo. com. Because the relationship between miles driven and price is negative, r < 0. Also, r is closer to – 1 than 0 because the relationship is strong. There isn’t much scatter from the linear pattern. Statistics and Probability with Applications, 3 rd Edition 5
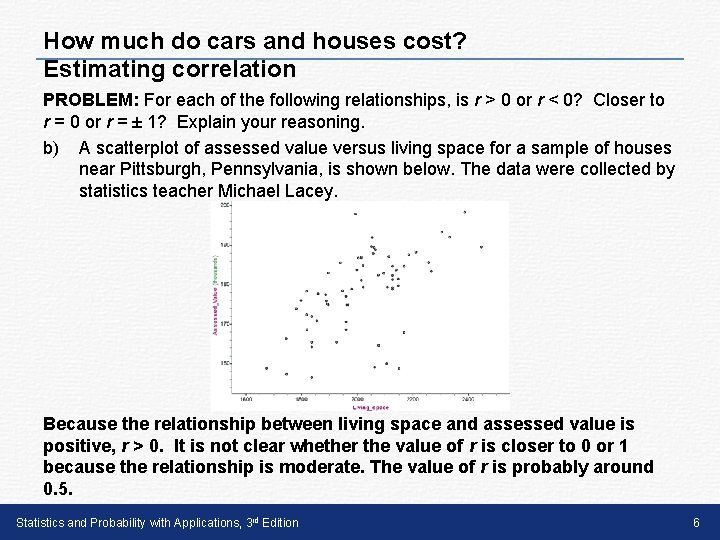
How much do cars and houses cost? Estimating correlation PROBLEM: For each of the following relationships, is r > 0 or r < 0? Closer to r = 0 or r = ± 1? Explain your reasoning. b) A scatterplot of assessed value versus living space for a sample of houses near Pittsburgh, Pennsylvania, is shown below. The data were collected by statistics teacher Michael Lacey. Because the relationship between living space and assessed value is positive, r > 0. It is not clear whether the value of r is closer to 0 or 1 because the relationship is moderate. The value of r is probably around 0. 5. Statistics and Probability with Applications, 3 rd Edition 6
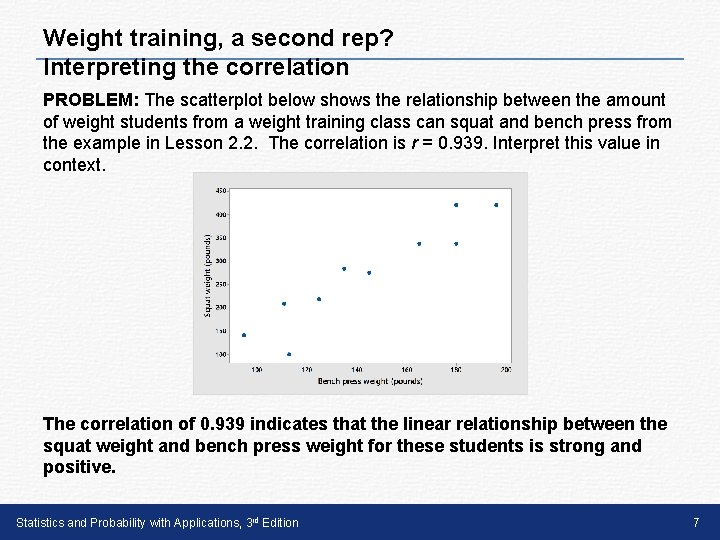
Weight training, a second rep? Interpreting the correlation PROBLEM: The scatterplot below shows the relationship between the amount of weight students from a weight training class can squat and bench press from the example in Lesson 2. 2. The correlation is r = 0. 939. Interpret this value in context. The correlation of 0. 939 indicates that the linear relationship between the squat weight and bench press weight for these students is strong and positive. Statistics and Probability with Applications, 3 rd Edition 7
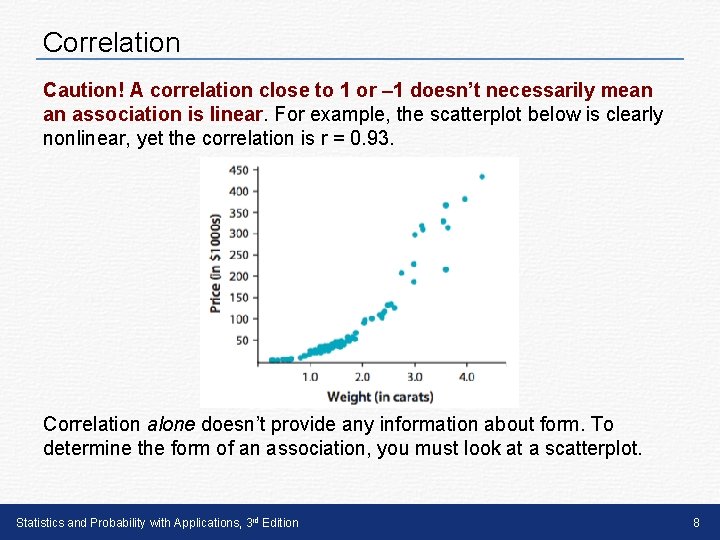
Correlation Caution! A correlation close to 1 or – 1 doesn’t necessarily mean an association is linear. For example, the scatterplot below is clearly nonlinear, yet the correlation is r = 0. 93. Correlation alone doesn’t provide any information about form. To determine the form of an association, you must look at a scatterplot. Statistics and Probability with Applications, 3 rd Edition 8
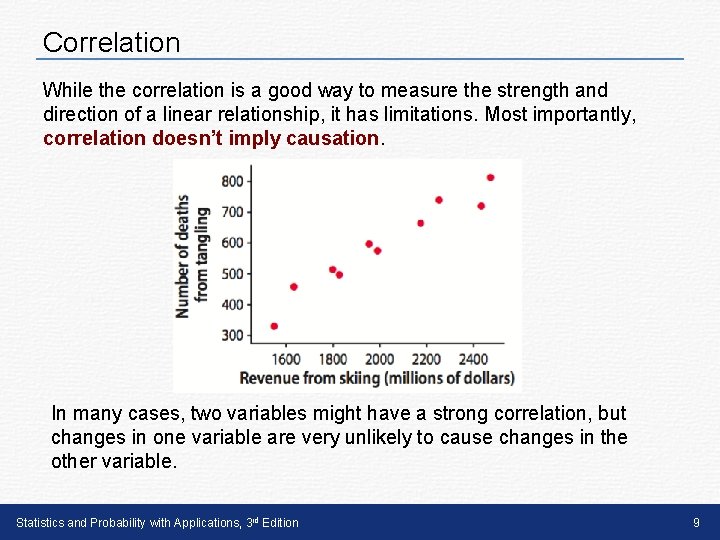
Correlation While the correlation is a good way to measure the strength and direction of a linear relationship, it has limitations. Most importantly, correlation doesn’t imply causation. In many cases, two variables might have a strong correlation, but changes in one variable are very unlikely to cause changes in the other variable. Statistics and Probability with Applications, 3 rd Edition 9
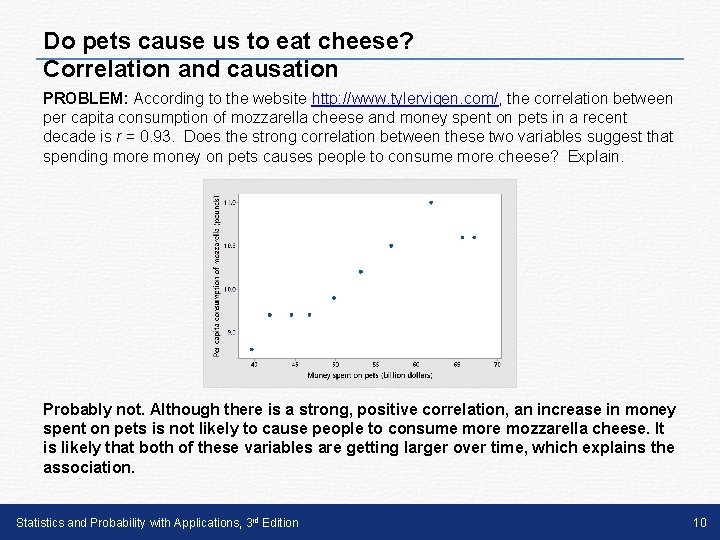
Do pets cause us to eat cheese? Correlation and causation PROBLEM: According to the website http: //www. tylervigen. com/, the correlation between per capita consumption of mozzarella cheese and money spent on pets in a recent decade is r = 0. 93. Does the strong correlation between these two variables suggest that spending more money on pets causes people to consume more cheese? Explain. Probably not. Although there is a strong, positive correlation, an increase in money spent on pets is not likely to cause people to consume more mozzarella cheese. It is likely that both of these variables are getting larger over time, which explains the association. Statistics and Probability with Applications, 3 rd Edition 10

LESSON APP 2. 3 If I eat more chocolate, will I win a Nobel prize? Most people love chocolate for its great taste. But does it also make you smarter? A scatterplot like this one recently appeared in the New England Journal of Medicine. The explanatory variable is the chocolate consumption person for a sample of countries. The response variable is the number of Nobel Prizes per 10 million residents of that country. 1. Interpret the correlation of r = 0. 791. 2. If people in the United States started eating more chocolate, can we expect more Nobel Prizes to be awarded to residents of the United States? Explain. Statistics and Probability with Applications, 3 rd Edition 11

LESSON APP 2. 3 If I eat more chocolate, will I win a Nobel prize? 1. Interpret the correlation of r = 0. 791. 2. If people in the United States started eating more chocolate, can we expect more Nobel Prizes to be awarded to residents of the United States? Explain. Statistics and Probability with Applications, 3 rd Edition 12

Correlation Learning Targets After this lesson, you should be able to: ü Estimate the correlation between two quantitative variables from a scatterplot. ü Interpret the correlation. ü Distinguish correlation from causation. Statistics and Probability with Applications, 3 rd Edition 13
- Slides: 13