2 Analyzing TwoVariable Data Lesson 2 5 Regression

2 Analyzing Two-Variable Data Lesson 2. 5 Regression Lines Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Regression Lines Learning Targets After this lesson, you should be able to: ü Make predictions using regression lines, keeping in mind the dangers of extrapolation. ü Calculate and interpret a residual. ü Interpret the slope and y intercept of a regression line. Statistics and Probability with Applications, 3 rd Edition 2

Regression Lines When the relationship between two quantitative variables is linear, we can use a regression line to model the relationship and make predictions. Regression Line A regression line is a line that describes how a response variable y changes as an explanatory variable x changes. Regression lines are expressed in the form where yˆ (pronounced “y hat”) is the predicted value of y for a given value of x. Statistics and Probability with Applications, 3 rd Edition 3
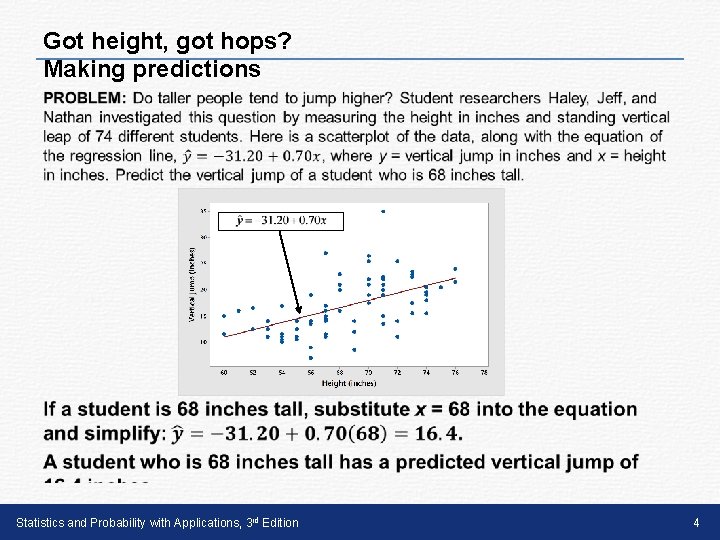
Got height, got hops? Making predictions • Statistics and Probability with Applications, 3 rd Edition 4
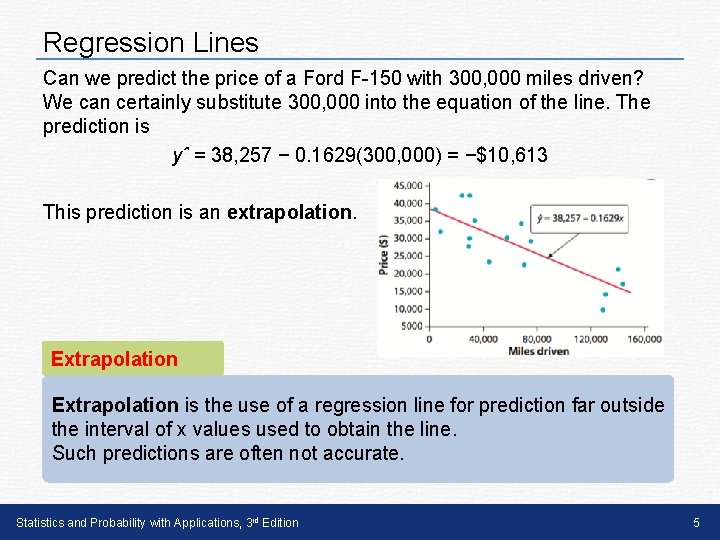
Regression Lines Can we predict the price of a Ford F-150 with 300, 000 miles driven? We can certainly substitute 300, 000 into the equation of the line. The prediction is yˆ = 38, 257 − 0. 1629(300, 000) = −$10, 613 This prediction is an extrapolation. Extrapolation is the use of a regression line for prediction far outside the interval of x values used to obtain the line. Such predictions are often not accurate. Statistics and Probability with Applications, 3 rd Edition 5

Regression Lines Even when we are not extrapolating, our predictions are seldom perfect. For a specific point, the difference between the actual value of y and the predicted value of y is called a residual. Residual A residual is the difference between an actual value of y and the value of y predicted by the regression line. That is, Statistics and Probability with Applications, 3 rd Edition 6
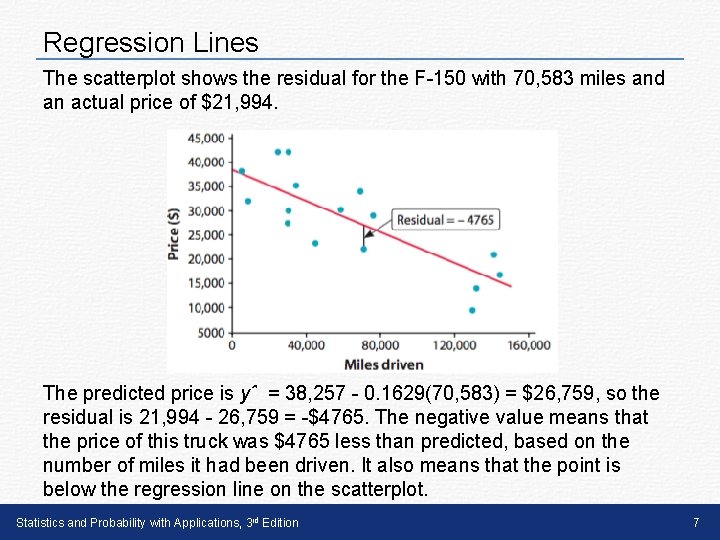
Regression Lines The scatterplot shows the residual for the F-150 with 70, 583 miles and an actual price of $21, 994. The predicted price is yˆ = 38, 257 - 0. 1629(70, 583) = $26, 759, so the residual is 21, 994 - 26, 759 = -$4765. The negative value means that the price of this truck was $4765 less than predicted, based on the number of miles it had been driven. It also means that the point is below the regression line on the scatterplot. Statistics and Probability with Applications, 3 rd Edition 7
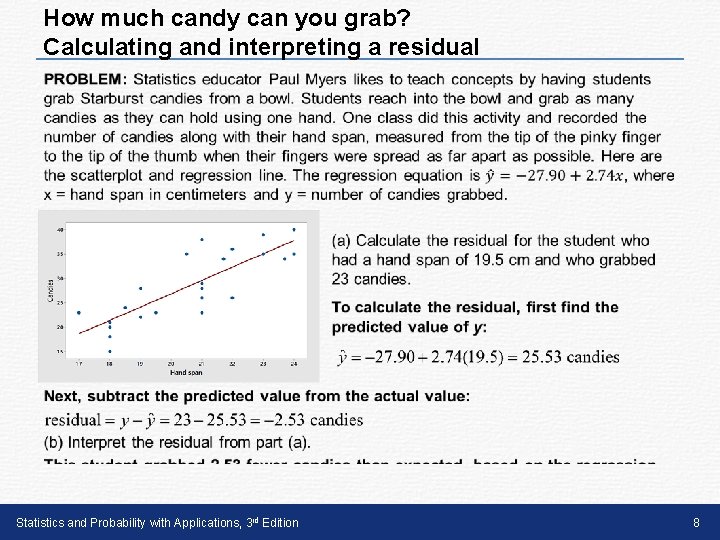
How much candy can you grab? Calculating and interpreting a residual • Statistics and Probability with Applications, 3 rd Edition 8

Regression Lines In the regression line ŷ = a + bx, a is the y intercept and b is the slope. Slope, y intercept The y intercept a is the predicted value of y when x = 0. The slope b of a regression line describes the predicted change in the y variable for each one-unit increase in the x variable. It is very important to include the word “predicted” (or its equivalent) in the interpretation of the slope and y intercept. Otherwise, it may seem that our predictions will be exactly correct. Statistics and Probability with Applications, 3 rd Edition 9

Grabbing more candy? Interpreting a regression line • Statistics and Probability with Applications, 3 rd Edition 10

LESSON APP 2. 5 Do cut flowers benefit from sugar in the water? Does adding sugar to the water in a vase help flowers stay fresh? To find out, two statistics students went to a flower shop and randomly selected 12 carnations. When they got home, the students prepared 12 identical vases with exactly the same amount of water in each vase. They put 1 tablespoon of sugar in 3 vases, 2 tablespoons of sugar in 3 vases, and 3 tablespoons of sugar in 3 vases. In the remaining 3 vases, they added no sugar. After the vases were prepared, the students randomly assigned 1 carnation to each vase and observed how many hours each flower continued to look fresh. Statistics and Probability with Applications, 3 rd Edition 11
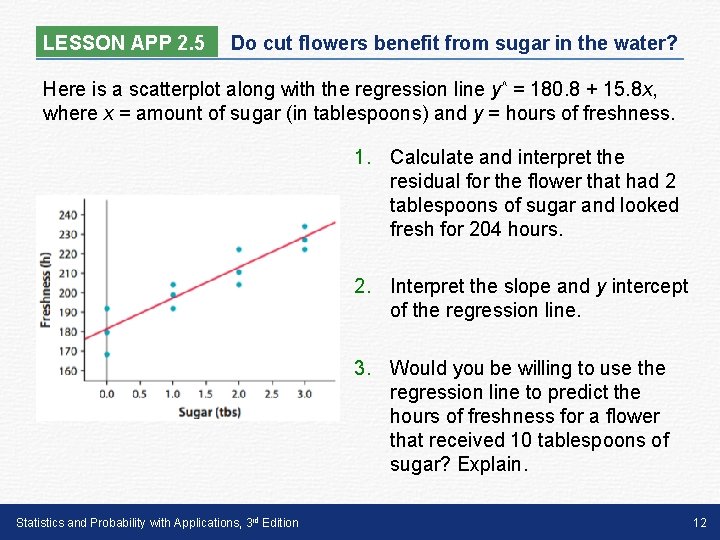
LESSON APP 2. 5 Do cut flowers benefit from sugar in the water? Here is a scatterplot along with the regression line y^ = 180. 8 + 15. 8 x, where x = amount of sugar (in tablespoons) and y = hours of freshness. 1. Calculate and interpret the residual for the flower that had 2 tablespoons of sugar and looked fresh for 204 hours. 2. Interpret the slope and y intercept of the regression line. 3. Would you be willing to use the regression line to predict the hours of freshness for a flower that received 10 tablespoons of sugar? Explain. Statistics and Probability with Applications, 3 rd Edition 12

LESSON APP 2. 5 Do cut flowers benefit from sugar in the water? 1. Calculate and interpret the residual for the flower that had 2 tablespoons of sugar and looked fresh for 204 hours. Statistics and Probability with Applications, 3 rd Edition 13

LESSON APP 2. 5 Do cut flowers benefit from sugar in the water? 2. Interpret the slope and y intercept of the regression line. 3. Would you be willing to use the regression line to predict the hours of freshness for a flower that received 10 tablespoons of sugar? Explain. Statistics and Probability with Applications, 3 rd Edition 14

Regression Lines Learning Targets After this lesson, you should be able to: ü Make predictions using regression lines, keeping in mind the dangers of extrapolation. ü Calculate and interpret a residual. ü Interpret the slope and y intercept of a regression line. Statistics and Probability with Applications, 3 rd Edition 15
- Slides: 15