2 Analyzing TwoVariable Data Lesson 2 2 Relationships

2 Analyzing Two-Variable Data Lesson 2. 2 Relationships Between Two Quantitative Variables Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Relationships Between Two Quantitative Variables Learning Targets After this lesson, you should be able to: ü Distinguish between explanatory and response variables for quantitative data. ü Make a scatterplot to display the relationship between two quantitative variables. ü Describe the direction, form, and strength of a relationship displayed in a scatterplot, and identify outliers. Statistics and Probability with Applications, 3 rd Edition 2

Relationships Between Two Quantitative Variables Although there are many ways to display the distribution of a single quantitative variable, a scatterplot is the best way to display the relationship between two quantitative variables. Scatterplot A scatterplot shows the relationship between two quantitative variables measured on the same individuals. The values of one variable appear on the horizontal axis, and the values of the other variable appear on the vertical axis. Each individual in the data set appears as a point in the graph. Statistics and Probability with Applications, 3 rd Edition 3
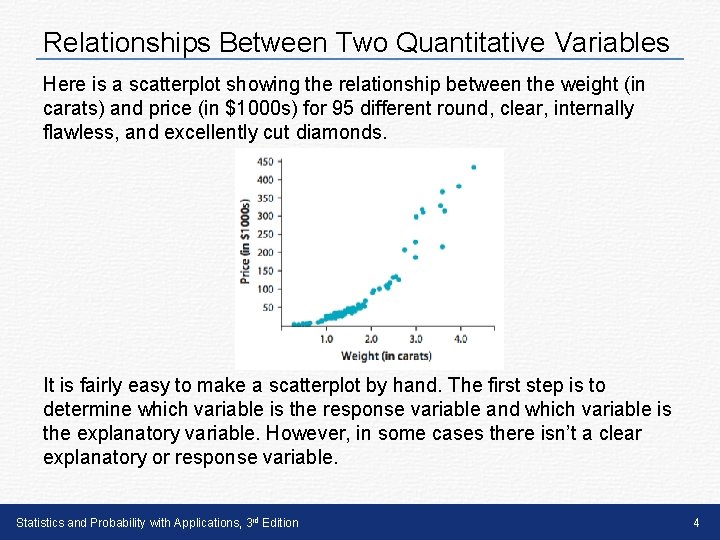
Relationships Between Two Quantitative Variables Here is a scatterplot showing the relationship between the weight (in carats) and price (in $1000 s) for 95 different round, clear, internally flawless, and excellently cut diamonds. It is fairly easy to make a scatterplot by hand. The first step is to determine which variable is the response variable and which variable is the explanatory variable. However, in some cases there isn’t a clear explanatory or response variable. Statistics and Probability with Applications, 3 rd Edition 4

Relationships Between Two Quantitative Variables How to Make a Scatterplot 1. Label the axes. The explanatory variable is plotted on the horizontal axis and the response variable is plotted on the vertical axis. If there is no explanatory variable, either variable can go on the horizontal axis. 2. Scale the axes. Put the name of the explanatory variable under the horizontal axis and place equally spaced tick marks along the axis beginning at a “friendly” number just below the smallest value of the explanatory variable and continuing until you exceed the largest value. Do the same for the response variable along the vertical axis. 3. Plot individual data values. For each individual, plot a point directly above that individual’s value for the explanatory variable and directly to the right of that individual’s value for the response variable. Statistics and Probability with Applications, 3 rd Edition 5

Relationships Between Two Quantitative Variables How to Describe a Scatterplot To describe a scatterplot, make sure to address the following four characteristics in the context of the data: • Direction: A scatterplot can show a positive association, negative association, or no association. In a positive association, above-average values of the explanatory variable tend to be paired with above-average values of the response variable and below-average values tend to be paired with below-average values. In a negative association, above-average values of the explanatory variable tend to be paired with below-average values of the response variable and vice-versa. • Form: A scatterplot can show a linear form or a nonlinear form. The form is linear if the overall pattern follows a straight line. Otherwise, the form is nonlinear. • Strength: A scatterplot can show a weak, moderate, or strong association. An association is strong if the points don’t deviate much from the form identified. An association is weak if the points deviate quite a bit from the form identified. • Outliers: Individual points that fall outside the overall pattern of the relationship. Statistics and Probability with Applications, 3 rd Edition 6
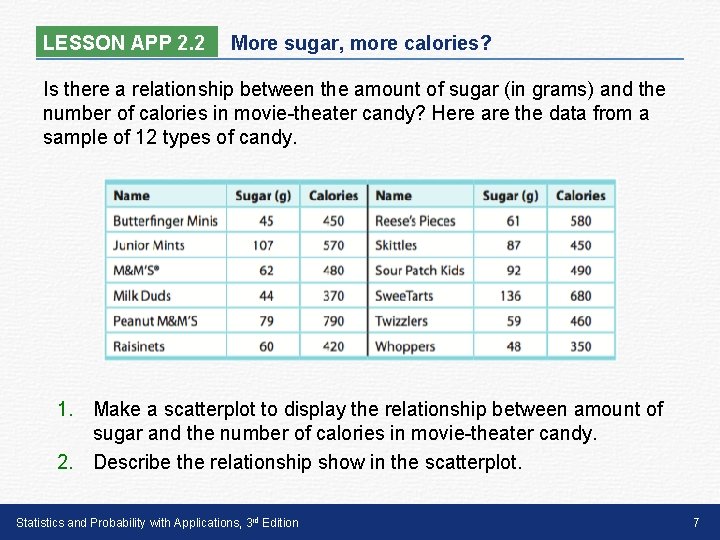
LESSON APP 2. 2 More sugar, more calories? Is there a relationship between the amount of sugar (in grams) and the number of calories in movie-theater candy? Here are the data from a sample of 12 types of candy. 1. Make a scatterplot to display the relationship between amount of sugar and the number of calories in movie-theater candy. 2. Describe the relationship show in the scatterplot. Statistics and Probability with Applications, 3 rd Edition 7

Relationships Between Two Quantitative Variables Learning Targets After this lesson, you should be able to: ü Distinguish between explanatory and response variables for quantitative data. ü Make a scatterplot to display the relationship between two quantitative variables. ü Describe the direction, form, and strength of a relationship displayed in a scatterplot, and identify outliers. Statistics and Probability with Applications, 3 rd Edition 8
- Slides: 8