2 Analyzing TwoVariable Data Lesson 2 4 Calculating

2 Analyzing Two-Variable Data Lesson 2. 4 Calculating the Correlation Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Calculating the Correlation Learning Targets After this lesson, you should be able to: ü Calculate the correlation between two quantitative variables. ü Apply the properties of the correlation. ü Describe how outliers influence the correlation. Statistics and Probability with Applications, 3 rd Edition 2

Calculating the Correlation In the previous lesson, we learned that the correlation r measures the strength and direction of the linear relationship between two quantitative variables. How to Calculate the Correlation r 1. Find the mean x-bar and the standard deviation sx of the explanatory variable. Calculate the z-score for the value of the explanatory variable for each individual. 2. Find the mean y-bar and the standard deviation sy of the response variable. Calculate the z-score for the value of the response variable for each individual. 3. For each individual, multiply the z-score for the explanatory variable and the z-score for the response variable. 4. Add the z-score products and divide the sum by n – 1. Statistics and Probability with Applications, 3 rd Edition 3
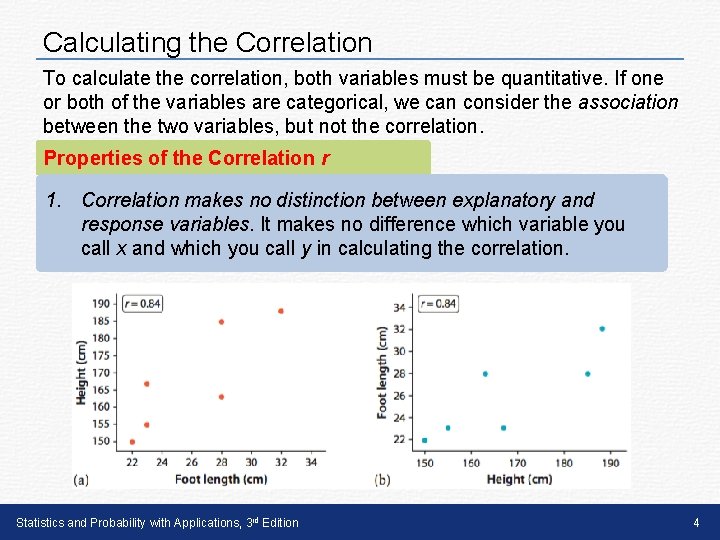
Calculating the Correlation To calculate the correlation, both variables must be quantitative. If one or both of the variables are categorical, we can consider the association between the two variables, but not the correlation. Properties of the Correlation r 1. Correlation makes no distinction between explanatory and response variables. It makes no difference which variable you call x and which you call y in calculating the correlation. Statistics and Probability with Applications, 3 rd Edition 4
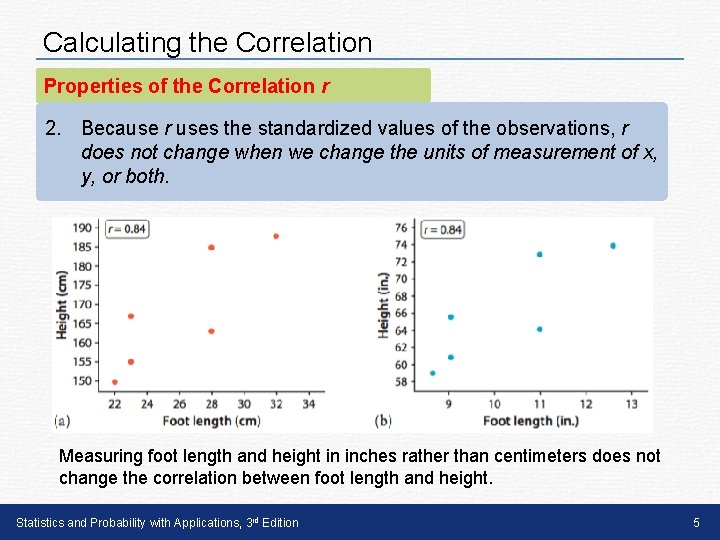
Calculating the Correlation Properties of the Correlation r 2. Because r uses the standardized values of the observations, r does not change when we change the units of measurement of x, y, or both. Measuring foot length and height in inches rather than centimeters does not change the correlation between foot length and height. Statistics and Probability with Applications, 3 rd Edition 5

Calculating the Correlation Properties of the Correlation r 3. The correlation r has no units of measurement because we are using standardized values in the calculation and standardized values have no units. Statistics and Probability with Applications, 3 rd Edition 6

Calculating the Correlation The formula for correlation involves the mean and standard deviation of both variables. Because the mean and standard deviation aren’t resistant to outliers, the correlation isn’t resistant to outliers either. Consider a scatterplot in which the majority of points form a positive, linear association. An outlier that is in the same pattern as the rest of the points will make the correlation closer to 1. An outlier that is not in the pattern of the rest of the points will make the correlation closer to 0—or possibly negative. Statistics and Probability with Applications, 3 rd Edition 7

LESSON APP 2. 4 Flying dinosaur or early bird? Archaeopteryx is an extinct beast having feathers like a bird, but teeth and a long bony tail like a reptile. Because the known specimens differ greatly in size, some scientists think they are different species rather than individuals from the same species. However, if the specimens belong to the same species and differ in size because some are younger than others, there should be a positive linear relationship between the lengths of a pair of bones from all individuals. An outlier from this relationship would suggest a different species. Here are data on the lengths (in centimeters) of the femur (a leg bone) and the humerus (a bone in the upper arm) for five specimens that preserve both bones. Statistics and Probability with Applications, 3 rd Edition 8

LESSON APP 2. 4 Flying dinosaur or early bird? 1. Make a scatterplot using length of femur as the explanatory variable. Do you think that all five specimens come from the same species? Explain. 1. Find the correlation r step by step, using the formula on page 121. Explain how your value for r matches your graph in part (1). 1. Suppose that a new fossil was discovered. If the femur is 70 centimeters and the humerus is 40 centimeters, do you think this specimen came from the same species? Explain. 1. What effect will the new fossil have on the correlation? Explain. Statistics and Probability with Applications, 3 rd Edition 9

Calculating the Correlation Learning Targets After this lesson, you should be able to: ü Calculate the correlation between two quantitative variables. ü Apply the properties of the correlation. ü Describe how outliers influence the correlation. Statistics and Probability with Applications, 3 rd Edition 10
- Slides: 10