Analyzing TwoVariable Data Lesson 2 3 Correlation Statistics

Analyzing Two-Variable Data Lesson 2. 3 Correlation Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Correlation Learning Targets After this lesson, you should be able to: ü Estimate the correlation between two quantitative variables from a scatterplot. ü Interpret the correlation. ü Distinguish correlation from causation. Statistics and Probability with Applications, 3 rd Edition 2

Correlation r Although the street definition of correlation applies to any two items that are related (such as gender and political affiliation), statisticians use this term only in the context of two numerical variables. The formal term for correlation is the correlation coefficient. Many different correlation measures have been created; the one we use in this class is called the Pearson correlation coefficient. Statistics and Probability with Applications, 3 rd Edition 3

S In the previous lesson, we used direction, form, and strength l � i to describe the association between two quantitative variables. d To quantify the strength of a linear relationship between two e quantitative variables, we use the correlation coefficient r 7 - The range of the correlation coefficient is -1 to 1 4 -1 If r = -1 there is a perfect negative correlation 0 If r is close to 0 there is no linear correlation Larson/Farber 4 th ed. Statistics and Probability with Applications, 3 rd Edition 1 If r = 1 there is a perfect positive correlation 44

Correlation r The correlation r is a measure of the strength and direction of a linear relationship between two quantitative variables. • The correlation r falls between − 1 and 1 (− 1 ≤ r ≤ 1). • If the relationship is negative, then r < 0. If the relationship is positive, then r > 0. • If r = 1 or r = − 1, then there is a perfect linear relationship. In other words, all of the points will be exactly on a line. • If there is very little scatter from the linear form, then r is close to 1 or − 1. The more scatter from the linear form, the closer r is to 0. r is calculated with the formula: Statistics and Probability with Applications, 3 rd Edition 5

FINDING CORRELATION ON THE CALCULATOR STAT > Calc To calculate r, you must first enter the Diagnostic. On command found in the Catalog menu r ≈ 0. 979 suggests a strong positive correlation. Larson/Farber 4 th ed. Statistics and Probability with Applications, 3 rd Edition 6 Slide 7 - 66
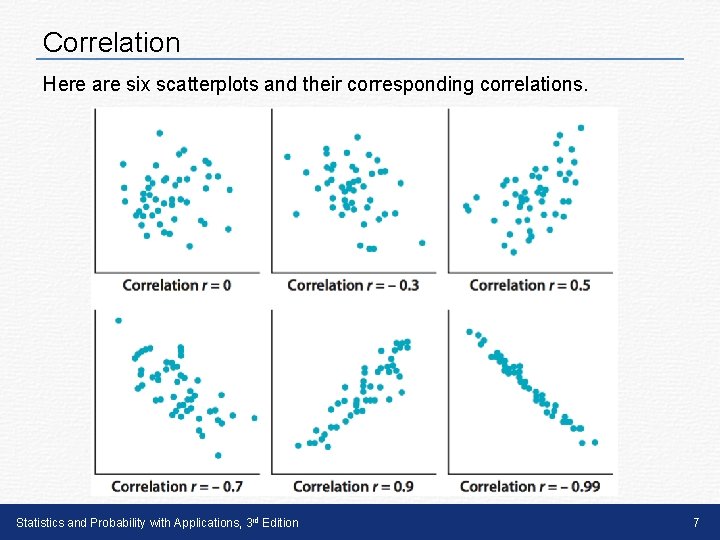
Correlation Here are six scatterplots and their corresponding correlations. Statistics and Probability with Applications, 3 rd Edition 7

How correlation behaves is more important than the details of the formula. Here are some important facts about r. 2. r does not change when we change the units of measurement of x, y, or both. 3. The correlation r itself has no unit of measurement. Cautions: • Correlation requires that both variables be quantitative. • Correlation does not describe curved relationships between variables, no matter how strong the relationship is. • Correlation is not resistant. r is strongly affected by a few outlying observations. • Correlation is not a complete summary of two-variable data. Scatterplots and Correlation 1. Correlation makes no distinction between explanatory and response variables. + • Facts about Correlation

S l i d e 7 9 Correlation Conditions • The Correlation Coefficient r measures the strength of the linear association between two quantitative variables. • Before you find r, you must check several conditions: – Quantitative Variables Condition – Straight Enough Condition – Outlier Condition Statistics and Probability with Applications, 3 rd Edition 9

S l i d e 7 1 0 Correlation Conditions • Quantitative Variables Condition: – Correlation applies only to quantitative variables. – Don’t apply correlation to categorical data masquerading as quantitative. – Check that you know the variables’ units and what they measure. Statistics and Probability with Applications, 3 rd Edition 10
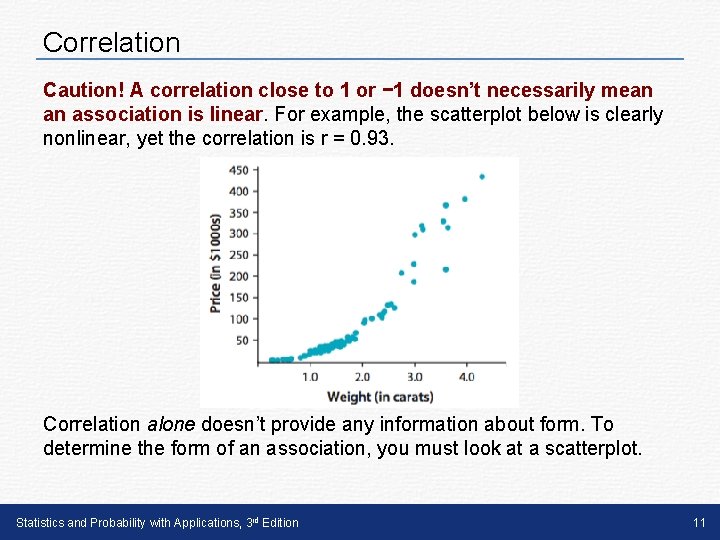
Correlation Caution! A correlation close to 1 or − 1 doesn’t necessarily mean an association is linear. For example, the scatterplot below is clearly nonlinear, yet the correlation is r = 0. 93. Correlation alone doesn’t provide any information about form. To determine the form of an association, you must look at a scatterplot. Statistics and Probability with Applications, 3 rd Edition 11
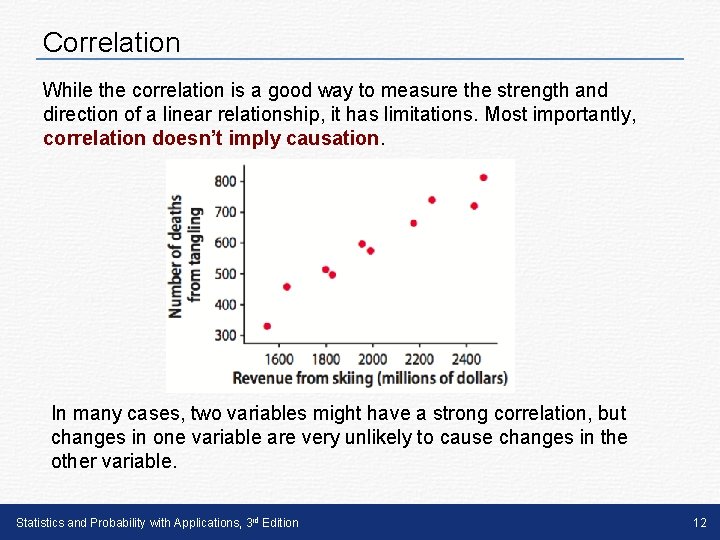
Correlation While the correlation is a good way to measure the strength and direction of a linear relationship, it has limitations. Most importantly, correlation doesn’t imply causation. In many cases, two variables might have a strong correlation, but changes in one variable are very unlikely to cause changes in the other variable. Statistics and Probability with Applications, 3 rd Edition 12

LESSON APP 2. 3 If I eat more chocolate, will I win a Nobel prize? Most people love chocolate for its great taste. But does it also make you smarter? A scatterplot like this one recently appeared in the New England Journal of Medicine. The explanatory variable is the chocolate consumption person for a sample of countries. The response variable is the number of Nobel Prizes per 10 million residents of that country. 1. Interpret the correlation of r = 0. 791. 2. If people in the United States started eating more chocolate, can we expect more Nobel Prizes to be awarded to residents of the United States? Explain. Statistics and Probability with Applications, 3 rd Edition 13

Correlation Learning Targets After this lesson, you should be able to: ü Estimate the correlation between two quantitative variables from a scatterplot. ü Interpret the correlation. ü Distinguish correlation from causation. Statistics and Probability with Applications, 3 rd Edition 14
- Slides: 14