Analyzing TwoVariable Data Lesson 2 8 Fitting Models

Analyzing Two-Variable Data Lesson 2. 8 Fitting Models to Curved Relationships Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Fitting Models to Curved Relationships Learning Targets After this lesson, you should be able to: ü Use technology to calculate quadratic models for curved relationships, then calculate and interpret residuals using the model. ü Use technology to calculate exponential models for curved relationships, then calculate and interpret residuals using the model. ü Use residual plots to determine the most appropriate model. Statistics and Probability with Applications, 3 rd Edition 2

Fitting Models to Curved Relationships When the association between two quantitative variables is linear, we use a least-squares regression line to model the relationship. When an association is nonlinear, we can use technology to calculate other types of models. In some cases, we can use a quadratic model to fit a nonlinear association between two quantitative variables. Quadratic Model A quadratic model is a model in the form yˆ = ax 2 +bx +c. The graph of a quadratic model is a parabola. Statistics and Probability with Applications, 3 rd Edition 3

Fitting Models to Curved Relationships The scatterplot below shows the relationship between passing yards and age for 32 quarterbacks in the 2010 NFL season. Statistics and Probability with Applications, 3 rd Edition 4

Fitting Models to Curved Relationships The association between passing yards and age is clearly nonlinear. Passing yards tend to be lower for younger and older quarterbacks and higher for “middle-aged” quarterbacks. Statistics and Probability with Applications, 3 rd Edition 5
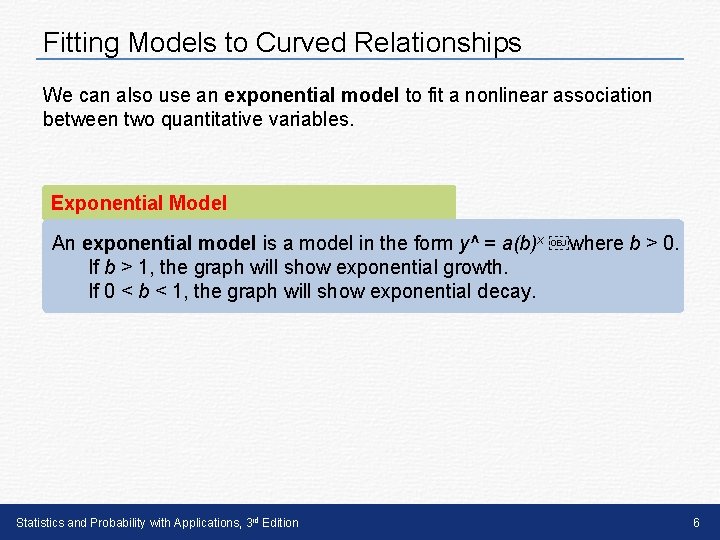
Fitting Models to Curved Relationships We can also use an exponential model to fit a nonlinear association between two quantitative variables. Exponential Model An exponential model is a model in the form y^ = a(b)x where b > 0. If b > 1, the graph will show exponential growth. If 0 < b < 1, the graph will show exponential decay. Statistics and Probability with Applications, 3 rd Edition 6
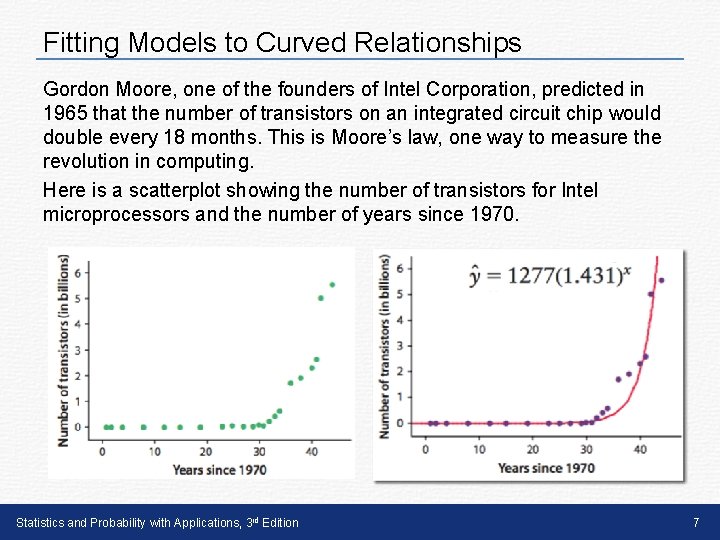
Fitting Models to Curved Relationships Gordon Moore, one of the founders of Intel Corporation, predicted in 1965 that the number of transistors on an integrated circuit chip would double every 18 months. This is Moore’s law, one way to measure the revolution in computing. Here is a scatterplot showing the number of transistors for Intel microprocessors and the number of years since 1970. Statistics and Probability with Applications, 3 rd Edition 7

In some cases, it is hard to tell if a quadratic model or an exponential model would be better to use. To decide, look at the residual plots for both models and choose the model with the residual plot that has the most random scatter. In Lesson 2. 7, we looked at the relationship between the cost of a 30 -second commercial during the Super Bowl and the Super Bowl number. The scatterplot to clearly shows that the relationship is nonlinear. An exponential model and a quadratic model were calculated for the relationship between cost and Super Bowl number. Here are the residual plots for these models. Based on the residual plots, which model is more appropriate? Explain. Statistics and Probability with Applications, 3 rd Edition 8
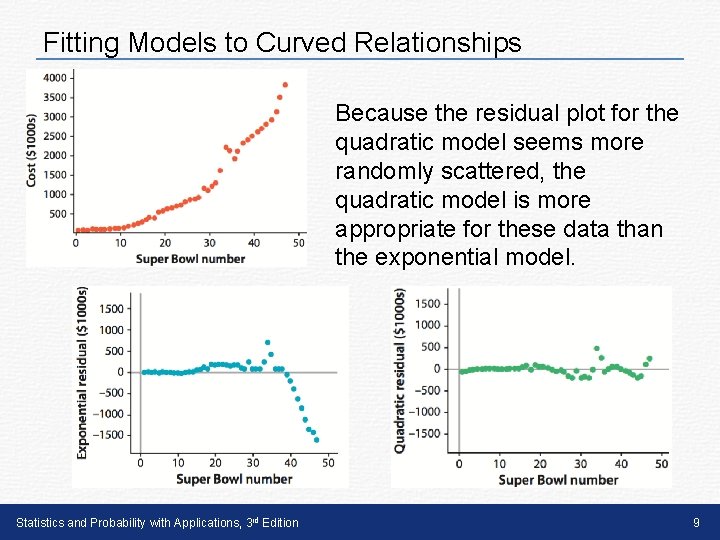
Fitting Models to Curved Relationships Because the residual plot for the quadratic model seems more randomly scattered, the quadratic model is more appropriate for these data than the exponential model. Statistics and Probability with Applications, 3 rd Edition 9
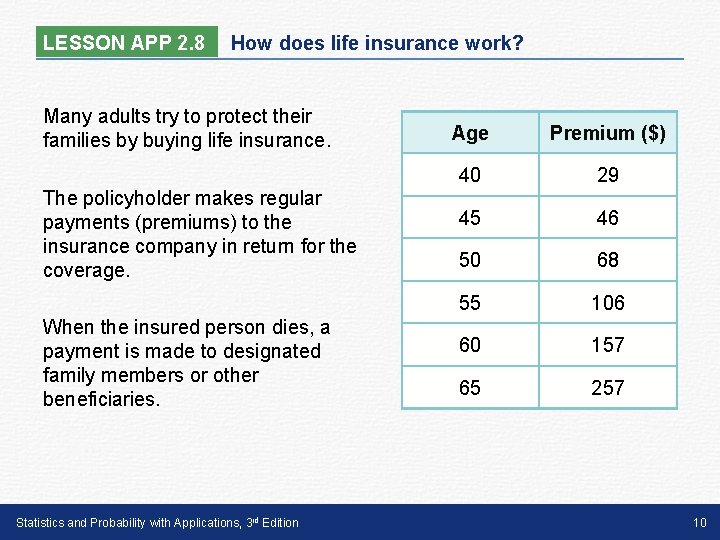
LESSON APP 2. 8 How does life insurance work? Many adults try to protect their families by buying life insurance. The policyholder makes regular payments (premiums) to the insurance company in return for the coverage. When the insured person dies, a payment is made to designated family members or other beneficiaries. Statistics and Probability with Applications, 3 rd Edition Age Premium ($) 40 29 45 46 50 68 55 106 60 157 65 257 10

LESSON APP 2. 8 How does life insurance work? How do insurance companies decide how much to charge for life insurance? They rely on a staff of highly trained actuaries—people with expertise in probability, statistics, and advanced mathematics—to determine premiums. If someone wants to buy life insurance, the premium will depend on the type and amount of the policy as well as on personal characteristics like age, gender, and health status. The table shows monthly premiums (in dollars) for a 10 -year term-life insurance policy worth $1, 000 for people of various ages (in years). Statistics and Probability with Applications, 3 rd Edition Age Premium ($) 40 29 45 46 50 68 55 106 60 157 65 257 11
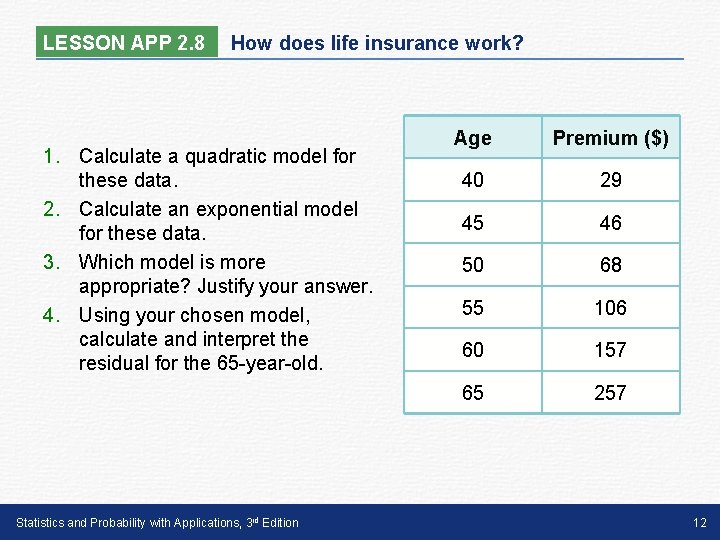
LESSON APP 2. 8 How does life insurance work? 1. Calculate a quadratic model for these data. 2. Calculate an exponential model for these data. 3. Which model is more appropriate? Justify your answer. 4. Using your chosen model, calculate and interpret the residual for the 65 -year-old. Statistics and Probability with Applications, 3 rd Edition Age Premium ($) 40 29 45 46 50 68 55 106 60 157 65 257 12

Fitting Models to Curved Relationships Learning Targets After this lesson, you should be able to: ü Use technology to calculate quadratic models for curved relationships, then calculate and interpret residuals using the model. ü Use technology to calculate exponential models for curved relationships, then calculate and interpret residuals using the model. ü Use residual plots to determine the most appropriate model. Statistics and Probability with Applications, 3 rd Edition 13
- Slides: 13