1 CHAPTER 5 CONVEX POLYTOPES Anastasiya Yeremenko Definitions








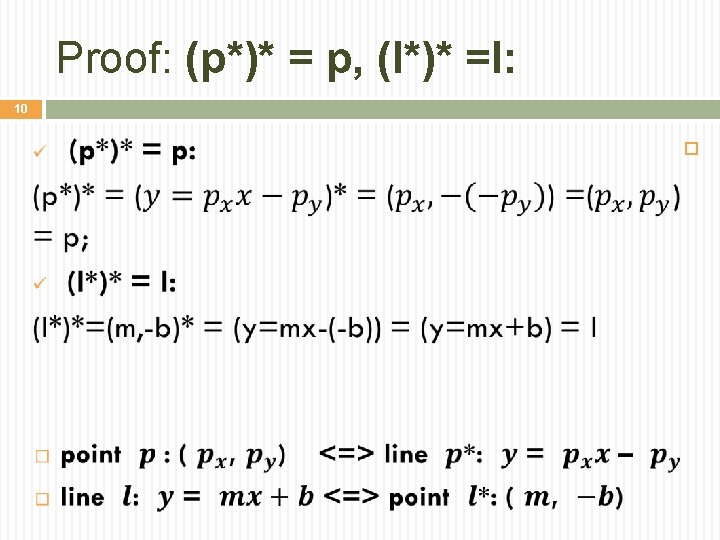













































- Slides: 59

1 CHAPTER 5: CONVEX POLYTOPES Anastasiya Yeremenko

Definitions 2

Examples: 3

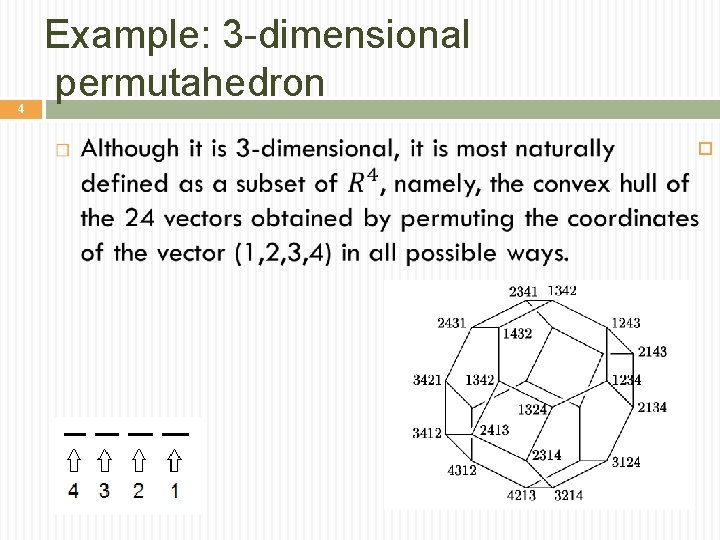
4 Example: 3 -dimensional permutahedron

Lecture slides: 5 Geometric Duality Ø H-Polytopes and V-Polytopes Ø Faces of a Convex Polytope Ø

Duality 2 D 6 Points (x, y) can be mapped in a one-to-one manner to lines (slope, intercept) in a different space. There are different ways to do this, called duality transforms.

7 Duality 2 D: One possible duality transform

8 Lemma: incidence and order preserving 2 D Let p be a point in the plane and let l be a nonvertical line in the plane. The duality transform * has the following properties: Ø It is incidence preserving: p∈l if and only if l*∈p* Ø It is order preserving: p lies above l if and only if l* lies above p*

9 Lemma: incidence and order preserving 2 D ü (p*)* = p, (l*)*=l ü p∈l if and only if l*∈p* ü p lies above l if and only if l* lies above p*
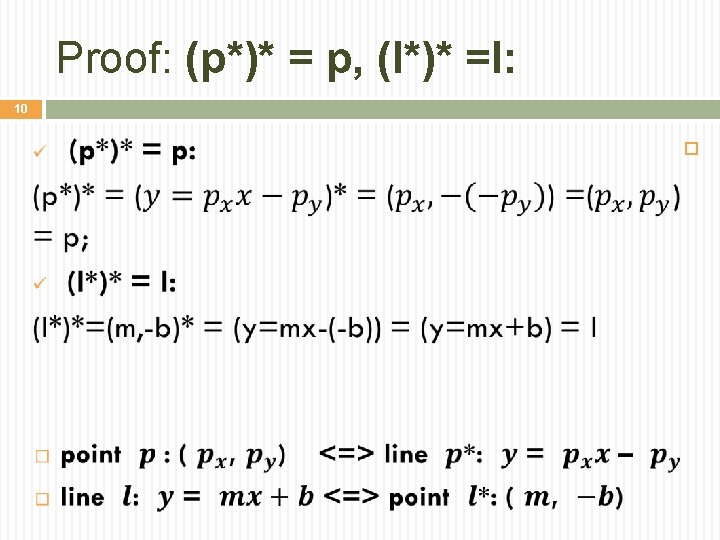
Proof: (p*)* = p, (l*)* =l: 10

Proof: p∈l if and only if l*∈p* 11

12 Proof: p lies above l if and only if l* lies above p*

Definition: 13

14 Lemma (Duality preserves incidences)

Definition: Geometric Duality 15

Geometric meaning of duality: 16

Geometric Duality 17

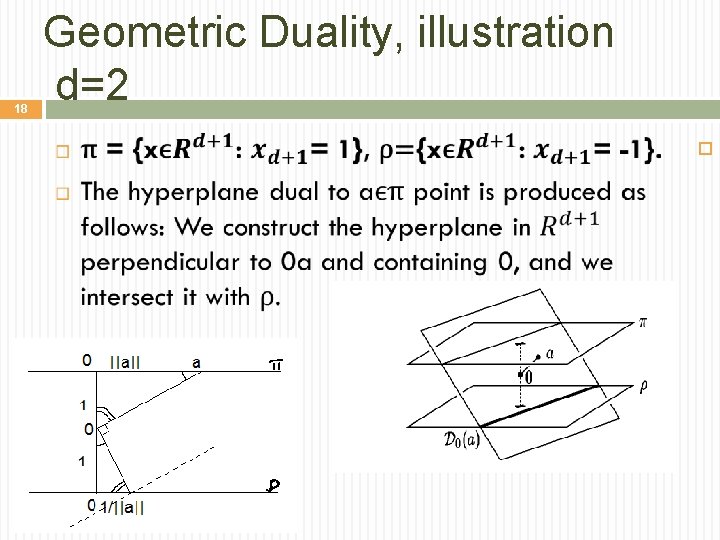
18 Geometric Duality, illustration d=2

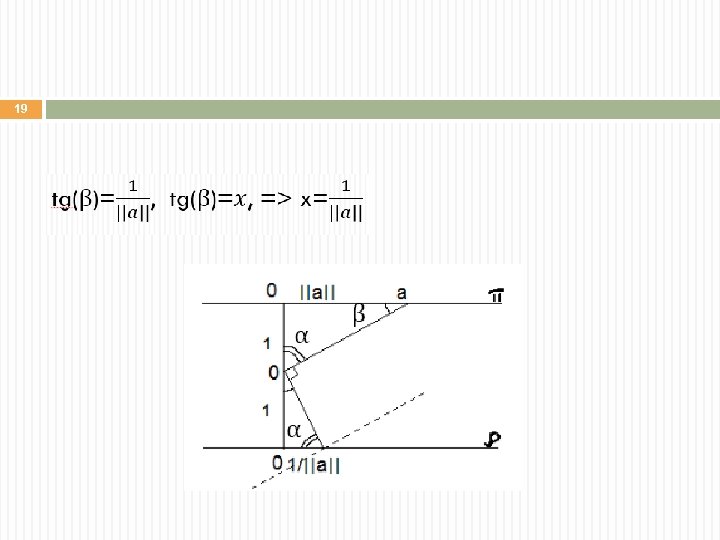
19

20 Lemma (Duality preserves incidences)

Proof of the Lemma 21

Definition: Dual Set 22

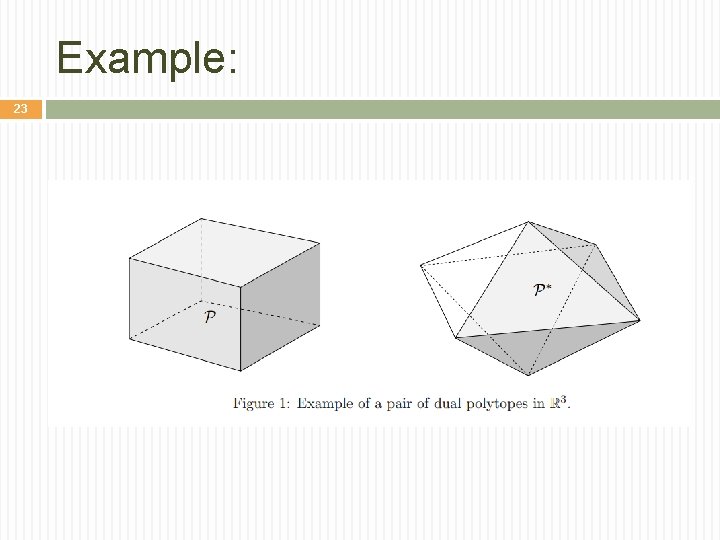
Example: 23

Dual Polytope 24 The dual polytope. Let P be a convex polytope containing the origin in its interior. Then the dual set P* is also a polytope. The dual of a cube is an octahedron, shown here with vertices at the cube face centers.

25 Geometric Duality

Geometric meaning of Dual Set: 26

27 H-Polytopes and V-Polytopes

Definition: H and V-polytope 28

Examples 29

Tetrahedron 30 It has 6 edges and 4 vertices, 4 faces.

Cube or Hexahedron 31 It has 12 edges and 8 vertices, 6 faces.

Octahedron 32 It has 12 edges and 6 vertices, 8 faces. A regular octahedron is a Platonic solid composed of 8 equilateral triangles, four of which meet at each vertex.

Dodecahedron 33 It is composed of 12 regular pentagonal faces, with three meeting at each vertex. It has 20 vertices, 30 edges. Its dual polyhedron is the icosahedron.

Icosahedron 34 In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It has five triangular faces meeting at each vertex.

35 H-polytopes and V-polytopes are equivalent A basic theorem about convex polytopes claims that from the mathematical point of view, Hpolytopes and V-polytopes are equivalent. Although H-polytopes and V-polytopes are mathematically equivalent, there is an enormous difference between them from the computational point of view. That is, it matters a lot whether a convex polytope is given to us as a convex hull of a finite set or as an intersection of half-spaces.

H and V Polytopes 36 For example, given a set of n points specifying a V-polytope, how do we find its representation as an H-polytope? It is not hard to come up with some algorithm, but the problem is to find an efficient algorithm that would allow one to handle large real-world problems.

37 Maximization of a given linear function over a given polytope. As another illustration of the computational difference between V-polytopes and Hpolytopes, we consider the maximization of a given linear function over a given polytope. For V-polytopes it is a trivial problem, since it suffices to substitute all points of V into the given linear function and select the maximum of the resulting values. But maximizing a linear function over the intersection of a collection of half-spaces is the basic problem of linear programming, and it is certainly nontrivial.

Basic Example: Cubes 38

Basic Example: Crosspolytopes 39

Definition: Simplex 40

41 Theorem: V and H-polytopes are equivalent Proof: Each H-polytope is a V-polytope. Proof: Each V-polytope is an H-polytope.

42 Proof: Each H-polytope is a Vpolytope.

43 Proof: Each H-polytope is a Vpolytope.

Proof: Each V-polytope is a Hpolytope. 44

45 Faces of a Convex Polytope A face of a convex polytope P is defined as • either P itself, or • a subset of P of the form P ∩ h, where h is a hyperplane such that P is fully contained in one of the closed half-spaces determined by h.

Faces 46 We observe that each face of P is a convex polytope. This is because P is the intersection of finitely many half-spaces and h is the intersection of two half-spaces, so the face is an H-polyhedron, and it is bounded. If P is a polytope of dimension d, then its faces have dimensions -1, 0, 1, . . . , d, where -1 is, by definition, the dimension of the empty set. A face of dimension j is also called a j-face.

47 Names of Faces for d dimensional polytope 0 -faces – vertices 1 -faces – edges (d-2)-faces - ridges (d-1)-faces - facets For example, the 3 -dimensional cube has 28 faces in total: the empty face, 8 vertices, 12 edges, 6 facets, and the whole cube

Extremal 48

Proposition(proof next lesson) 49

Graphs of polytopes. 50 Each 1 -dimensional face, or edge, of a convex polytope has exactly two vertices. We can thus define the graph G(P) of a polytope P in the natural way: The vertices of the polytope are vertices of the graph, and two vertices are connected by an edge in the graph if they are vertices of the same edge of P.

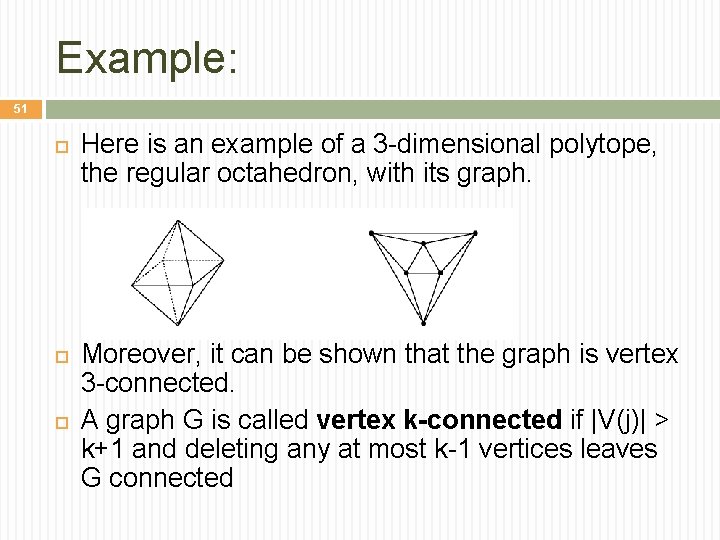
Example: 51 Here is an example of a 3 -dimensional polytope, the regular octahedron, with its graph. Moreover, it can be shown that the graph is vertex 3 -connected. A graph G is called vertex k-connected if |V(j)| > k+1 and deleting any at most k-1 vertices leaves G connected

Theorem (Steinitz theorem). 52 A finite graph is isomorphic to the graph of a 3 -dimensional convex polytope if and only if it is planar and vertex 3 -connected. Note: Graphs of higher-dimensional polytopes probably have no nice description comparable to the 3 -dimensional case, and it is likely that the problem of deciding whether a given graph is isomorphic to a graph of a 4 -dimensional convex polytope is NP-hard.

Examples 53

Examples 54

The face lattice. 55 Let F(P) be the set of all faces of a (bounded) convex polytope P (including the empty face ∅ of dimension -1). We consider the partial ordering of F(P) by inclusion.

56 The face lattice can be a suitable representation of a convex polytope in a computer. Each j-face is connected by pointers to its (j-1)-faces and to the (j+1)-faces containing it.

Definition: Simple and simplicial polytopes 57 A polytope P is called simplicial if each of its facets is a simplex (this happens, in particular, if the vertices of P are in general position, but general position is not necessary). A d-dimensional polytope P is called simple if each of its vertices is contained in exactly d facets.

Platonic solids 58 Among the five Platonic solids, the tetrahedron, the octahedron, and the icosahedron are simplicial; and the tetrahedron, the cube, and the dodecahedron are simple.

More examples: 59 The dual of a simple polytope is simplicial, and vice versa. The dual of a cube is an octahedron, shown here with vertices at the cube face centers.
 Convex polygons examples
Convex polygons examples Convex hull is the smallest convex set
Convex hull is the smallest convex set Yasiv com vk
Yasiv com vk Cs 154 stanford
Cs 154 stanford Anastasiya pronina
Anastasiya pronina Parallelism for paired ideas
Parallelism for paired ideas Chapter 13 sentence check 2 answer key
Chapter 13 sentence check 2 answer key Convex weld symbol
Convex weld symbol Pole in polar coordinates
Pole in polar coordinates Converging lens ray diagram
Converging lens ray diagram Polygons definition
Polygons definition Which of these are concave polygons
Which of these are concave polygons Poligon
Poligon Limacon rules
Limacon rules Convex vs concave teeth
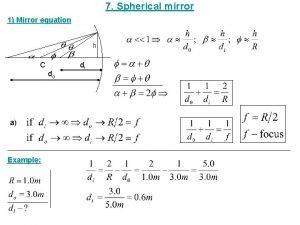
Convex vs concave teeth Mirror and lens equation
Mirror and lens equation A lens that curve outwards and are fatter in the middle
A lens that curve outwards and are fatter in the middle Salt mirror physics
Salt mirror physics Concave mirror and convex lens
Concave mirror and convex lens Concave lens simulation
Concave lens simulation Traction of joints
Traction of joints Perfect substitutes utility function
Perfect substitutes utility function Converging lens image characteristics
Converging lens image characteristics Limacon
Limacon Convex heptagon
Convex heptagon Elbow rom
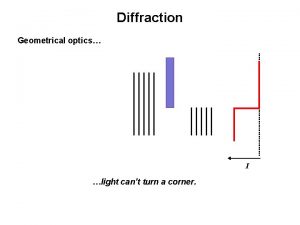
Elbow rom Fresnel and fraunhofer diffraction
Fresnel and fraunhofer diffraction Convex profile
Convex profile Convex and concave
Convex and concave Convex optimization in machine learning javatpoint
Convex optimization in machine learning javatpoint Converging lens in water
Converging lens in water Convex lens thicker
Convex lens thicker Dynamic convex hull
Dynamic convex hull Concave vs convex polygon
Concave vs convex polygon Convex vs concave lens
Convex vs concave lens Convex lens focal length
Convex lens focal length Convex hull collision detection
Convex hull collision detection Salt for concave mirrors
Salt for concave mirrors Colony morphologies
Colony morphologies Planar polygons
Planar polygons It is flat smooth mirror
It is flat smooth mirror Convex lens ray diagram
Convex lens ray diagram Name of a regular polygon of 4 sides
Name of a regular polygon of 4 sides Concave mirror matter
Concave mirror matter What is the measure
What is the measure Convex
Convex Rules for obtaining image formed by concave lens
Rules for obtaining image formed by concave lens Convex hull
Convex hull Geometric optics in everyday life
Geometric optics in everyday life Convex mirror is a diverging mirror
Convex mirror is a diverging mirror Single concave spherical mirrors produce images that
Single concave spherical mirrors produce images that Distance of image formula
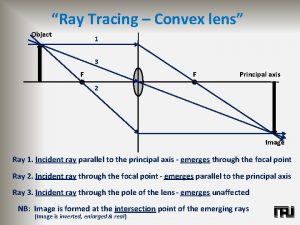
Distance of image formula Ray tracing convex lens
Ray tracing convex lens Irregularities in population pyramids
Irregularities in population pyramids Convex population pyramid
Convex population pyramid Trapez inscriptibil
Trapez inscriptibil Convex 39m series 60m
Convex 39m series 60m Converging lens shape
Converging lens shape Square edge convex
Square edge convex Convex
Convex