Zklady statistick indukce Pro stat data hledme vhodn

Základy statistické indukce Pro stat. data hledáme vhodné pravděp. modely, odhadujeme hodnoty jejich parametrů či testujeme tvrzení o chování stat. veličin. Využíváme toho, že charakteristiky stat. dat (např. aritm. průměr) vykazují vlastnosti pravděpodobnostních rozdělení.

Základy statistické indukce BODOVÉ ODHADY (tj. odhady jedním číslem) Tn (např. aritm. průměr či medián) je z dat získaný bodový odhad pro neznámý parametr q v pravděpodobnostním modelu pro sledovanou veličinu (např. pro střední hodnotu v normálním rozdělení). Je to odhad nestranný E(Tn)= q.

Základy statistické indukce Tabulka teoretických (neznámých a tudíž odhadovaných) parametrů a jejich nejvhodnějších (nestranných) odhadů: PARAMETR q JEHO BODOVÝ ODHAD Tn π = P(A) p = relativní četnost jevu A μ (střední hodnota) aritmetický průměr σ2 (rozptyl) výběrový rozptyl s 2 =M 2·n/(n-1)

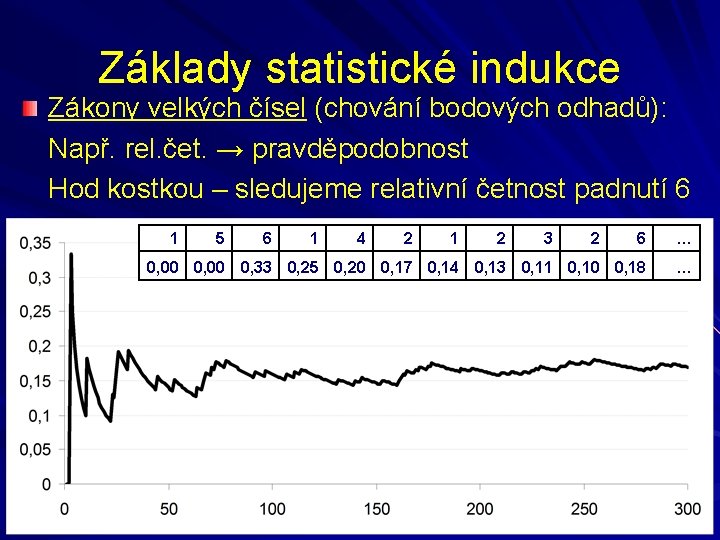
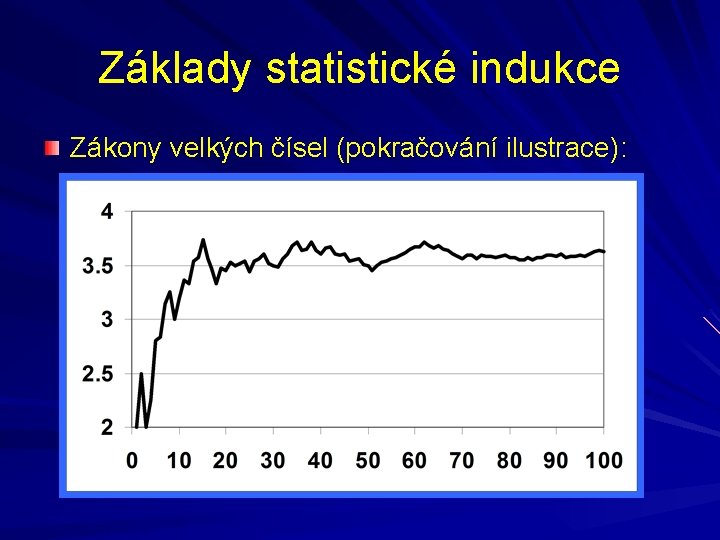
Základy statistické indukce Zákony velkých čísel (chování bodových odhadů): Např. rel. čet. → pravděpodobnost Hod kostkou – sledujeme relativní četnost padnutí 6 1 5 6 1 4 0, 00 0, 33 0, 25 0, 20 2 1 2 3 2 6 … 0, 17 0, 14 0, 13 0, 11 0, 10 0, 18 …

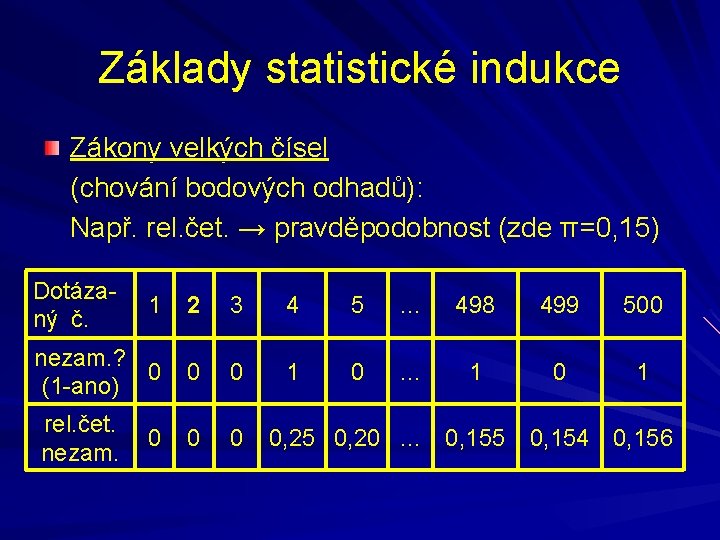
Základy statistické indukce Zákony velkých čísel (chování bodových odhadů): Např. rel. čet. → pravděpodobnost (zde π=0, 15) Dotázaný č. 1 2 3 4 5 … 498 499 500 nezam. ? 0 (1 -ano) 0 0 1 0 … 1 0 1 rel. čet. nezam. 0 0, 25 0, 20 … 0, 155 0, 154 0, 156

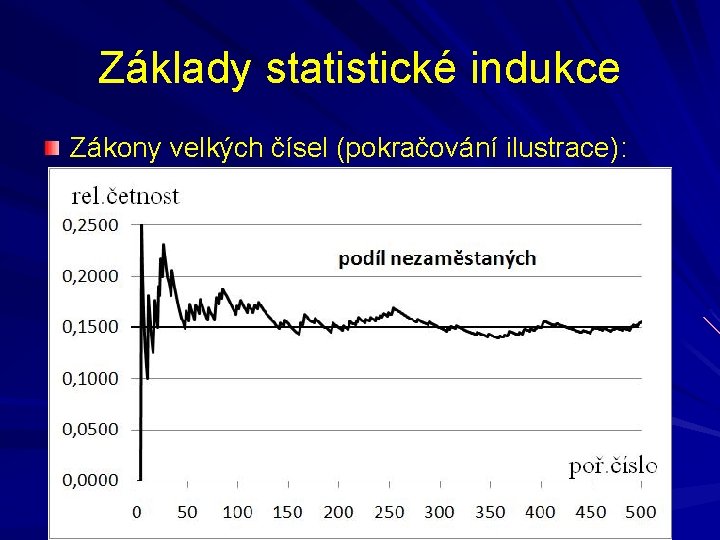
Základy statistické indukce Zákony velkých čísel (pokračování ilustrace):

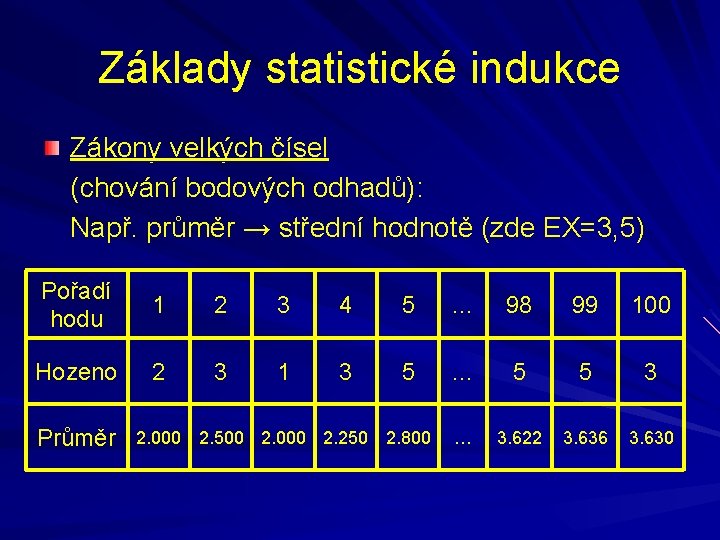
Základy statistické indukce Zákony velkých čísel (chování bodových odhadů): Např. průměr → střední hodnotě (zde EX=3, 5) Pořadí hodu 1 2 3 4 5 … 98 99 100 Hozeno 2 3 1 3 5 … 5 5 3 … 3. 622 3. 636 3. 630 Průměr 2. 000 2. 500 2. 000 2. 250 2. 800

Základy statistické indukce Zákony velkých čísel (pokračování ilustrace):

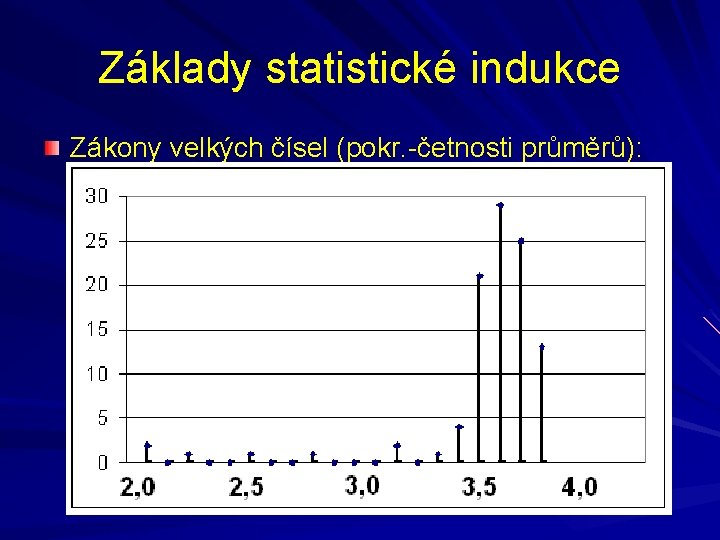
Základy statistické indukce Zákony velkých čísel (pokr. -četnosti průměrů):

Základy statistické indukce Centrální limitní věty (CLV) Popisují asymptotické (tj. v limitě, v praxi pro „dostatečně velký“ počet stat. dat) chování testových charakteristik Tn jakožto náhodných veličin. Např. _ Tn = (x−μ) / (σ/√n) → U ~ N(0, 1)

Intervaly spolehlivosti = intervalové odhady neznámého parametru (odhad pro , , 2, …), odvozují se z příslušné CLV spolehlivost = 1– = pravděpodobnost, že neznámá hodnota parametru je intervalem pokryta; nejčastěji volba 1– = 0, 95 (95% I. S. )

Oboustranné intervaly spolehlivosti Pro střední hodnotu μ při známém σ: _ x ± u 1 -α/2 σ/√n Pro střední hodnotu μ při neznámém σ: _ x ± t 1 -α/2 (n-1) s/√n kde n-1= počet stupňů volnosti (DF)

Oboustranné intervaly spolehlivosti Pro střední hodnotu μ - vzorce:

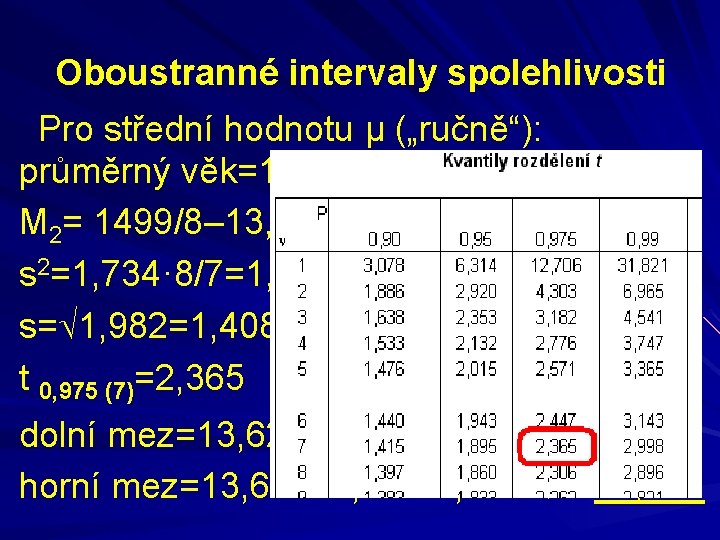
Oboustranné intervaly spolehlivosti Pro střední hodnotu μ („ručně“): Př. Dle věku osmi náhodně vybraných čtenářů dětského časopisu odhadněte střední věk čtenářů tohoto časopisu. Věky popořadě: 12, 14, 15, 12, 15, 14, 12, 15.

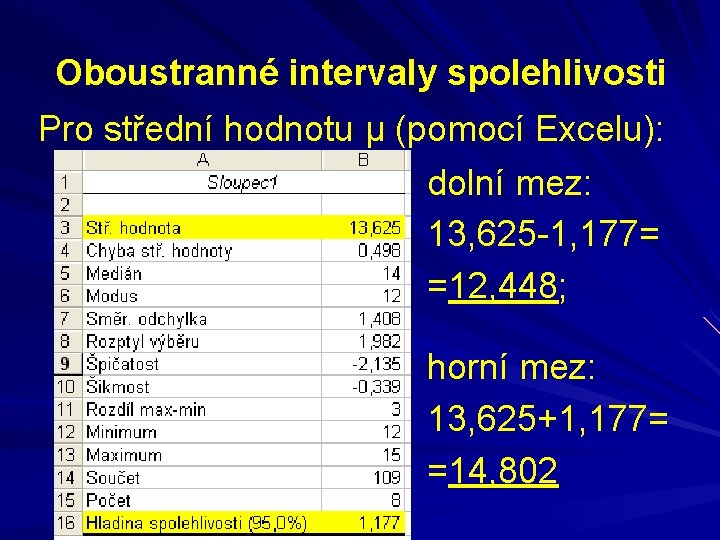
Oboustranné intervaly spolehlivosti Pro střední hodnotu μ („ručně“): průměrný věk=109/8=13, 625 M 2= 1499/8– 13, 6252=1, 734 s 2=1, 734· 8/7=1, 982 s= 1, 982=1, 408 t 0, 975 (7)=2, 365 dolní mez=13, 625– 2, 365· 1, 408/√ 8=12, 448 horní mez=13, 625+2, 365· 1, 408/√ 8=14, 802

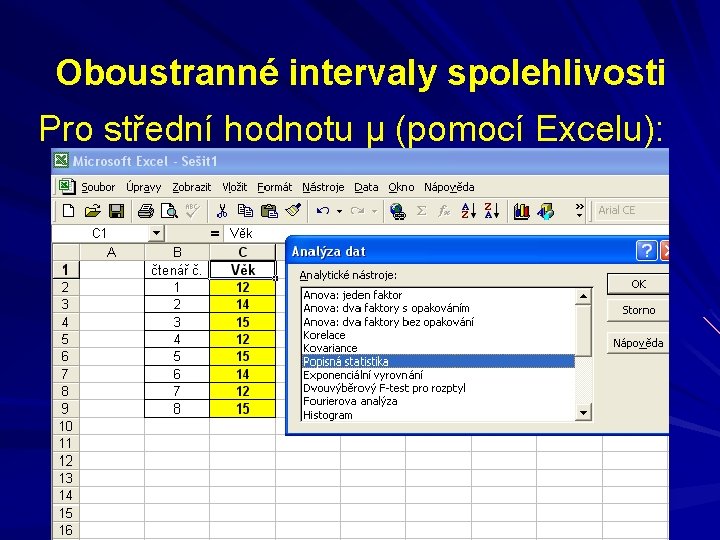
Oboustranné intervaly spolehlivosti Pro střední hodnotu μ (pomocí Excelu):

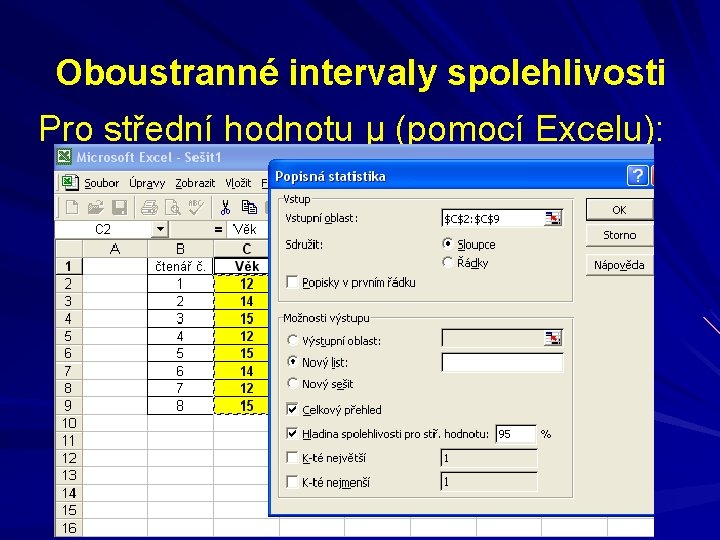
Oboustranné intervaly spolehlivosti Pro střední hodnotu μ (pomocí Excelu):

Oboustranné intervaly spolehlivosti Pro střední hodnotu μ (pomocí Excelu):

Oboustranné intervaly spolehlivosti Pro střední hodnotu μ (pomocí Excelu): dolní mez: 13, 625 -1, 177= =12, 448; horní mez: 13, 625+1, 177= =14, 802

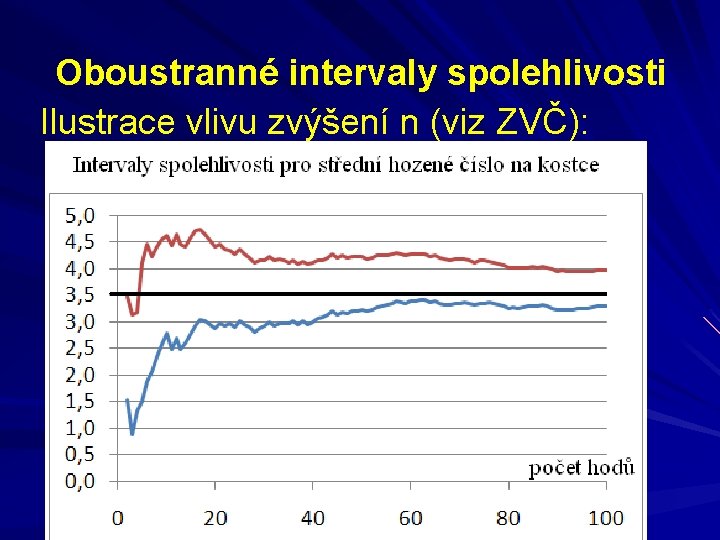
Oboustranné intervaly spolehlivosti Pro střední hodnotu μ (odpověď): S 95% spolehlivostí je střední věk čtenářů daného časopisu z rozmezí 12, 448 až 14, 802 roku. Zpřesnění odhadu (tj. zúžení IS)? a) zvýšit n (=změna dat); b) snížit spolehlivost (data stejná); c) snížit variabilitu (=změna populace).

Oboustranné intervaly spolehlivosti Ilustrace vlivu zvýšení n (viz ZVČ):

Oboustranné intervaly spolehlivosti Pro neznámý rozptyl σ2: (n-1)s 2/ א 2α/2(n-1) ; (n-1)s 2/ א 21 -α/2(n-1) Pro pravděpodobnost π: p-1/(2 n)-u 1 -α/2√[p(1 -p)/(n-1)] ; p+1/(2 n)+u 1 -α/2√[p(1 -p)/(n-1)]

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (vzorec):

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): Př. Dle odpovědí 12 dotazovaných, zda jsou nezaměstnaní, odhadněte s 90% spolehlivostí podíl nezaměstnaných v dané populaci. Data: mezi 12 tázanými byli 3 nezaměstnaní

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): n=12; p=3/12=0, 250; u 0, 95=1, 645 dolní mez = = 0, 250 – 1/24 – 1, 645· (0, 25· 0, 75/11) = = 0, 250 – 0, 256 = -0, 006; horní mez = 0, 250 + 0, 256 = 0, 506

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): Odpověď: S 90% spolehlivostí tvoří nezaměstnaní 0 % až 50, 6 % populace (? ) Zde nutné zpřesnění odhadu (zúžení IS): a) zvýšením n (mnohem víc tázaných); b) snížit spolehlivost.

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): Př. pokračování (obvyklý problém): V úloze s nezaměstnaností odhadněte předem potřebný počet tázaných k tomu, aby celková šířka výsledného intervalu spolehlivosti nepřesáhla 10 %.

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): Předpoklady: n … nyní neznáme; p … zřejmě bude opět cca 0, 250 kvantil bude opět u 0, 95=1, 645

Oboustranné intervaly spolehlivosti Pro pravděpodobnost π (ručně): Chceme, aby výsledný IS měl tvar: 0, 25– 0, 05=0, 20 (dolní mez) až 0, 25+0, 05=0, 30 (horní mez) – tak je celková šířka IS právě 10 %; tudíž musí platit: 1/(2 n)+1, 645· [0, 25· 0, 75/(n-1)] = 0, 05

Oboustranné intervaly spolehlivosti Pro zjednodušení předpokládejme, že 1/(2 n)=0 (n bude velké), řešíme pak: 1, 645· [0, 25· 0, 75/(n-1)] = 0, 05 |: 1, 645 [0, 1875/(n-1)] = 0, 0304 |2 0, 1875/(n-1) = 0, 0009 |·(n-1) 0, 1875 = 0, 0009·(n-1) |: 0, 0009 203 = n-1 |+1 n = 204 (=odhad rozsahu průzkumu)

Jednostranné intervaly spolehlivosti hledáme jen jednu z obou mezí Princip: dle zadání úlohy hledáme jen dolní či jen horní mez podle „oboustranného“ vzorce s tou změnou, že výraz 1 -α/2 ve vzorci nahradíme výrazem 1 -α. Příklad: Odhadněte horní hranici nezaměstnanosti. Řešení: Určujeme p+1/(2 n)+u 1 -α√[p(1 -p)/(n-1)]. (Konkrétní úlohy viz Sbírka úloh. )