Statistick termodynamika L 10 Statistick termodynamika kapalin 1

Statistická termodynamika – L 10 Statistická termodynamika kapalin. 1. Buňková teorie kapalin a stlačených plynů. Kritické veličiny. Teorém korespondujících stavů. 2. Koncepce volného objemu kapalin. Výpočet tlaku nasycených par. 3. Distribuční funkce v jednoatomových kapalinách. Radiální korelační funkce. 1

Modely kapalin Představa isolovaných molekul, jako v plynech, je nevhodná. Uspořádání v kapalinách za nízkých teplot: blízké představě pevné látky (pseudomřížka). Specifický model pro kapaliny: buňková teorie (kvazimřížka). teorie volného objemu Jedna složka. 2

1. Buňková teorie kapalin Kvazimřížka: Zachovává symetrii krystalu z něhož kapalina vznikla. Molekuly v kapalině jsou obklopeny „sousedy“–tvoří „buňku“ Stěny buňky tvoří kulově symetrické silové pole „sousedů“, které působí na každou molekulu nezávisle na čase. Migrace molekul mezi buňkami je povolena. (Molekuly mohou vykonávat translační pohyb. ) 3

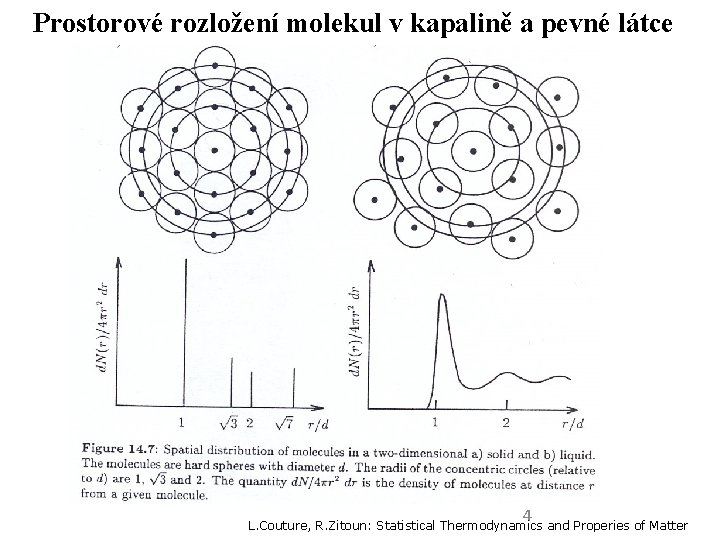
Prostorové rozložení molekul v kapalině a pevné látce 4 L. Couture, R. Zitoun: Statistical Thermodynamics and Properies of Matter

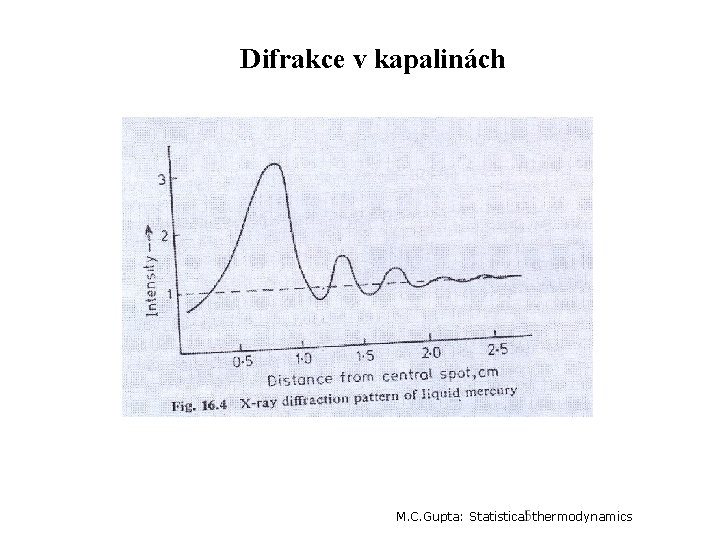
Difrakce v kapalinách 5 M. C. Gupta: Statistical thermodynamics

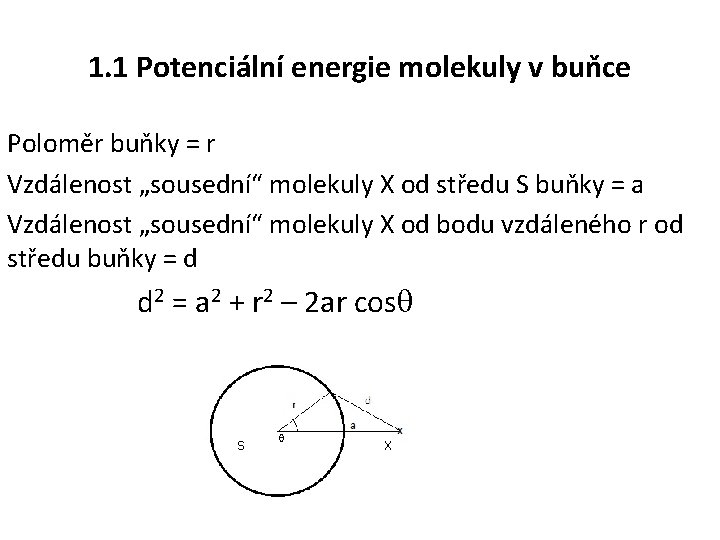
1. 1 Potenciální energie molekuly v buňce Poloměr buňky = r Vzdálenost „sousední“ molekuly X od středu S buňky = a Vzdálenost „sousední“ molekuly X od bodu vzdáleného r od středu buňky = d d 2 = a 2 + r 2 – 2 ar cos S X 6

Průměrná potenciální energie molekuly v buňce vůči „sousední“ molekule vzdálené „a“ od středu buňky je u(r) = ½ o u(d) sin d Pro potenciálovou funkci u(d) použijeme Lenardův-Jonesův (LJ) potenciál 12 -6 (L 9): U(d) = 4 ( ( /d)12 – ( /d)6 ) = ( ( vd. W/d)12 – 2 ( vd. W/d)6 ) ( je hloubka potenciálového minima, vzdálenost molekul pro U=0, vd. W táž vzdálenost podle van der Waalsovy rovnice): Vzdálenost „sousedů“ vypočteme pomocí celkového objemu V: d-12 = (N/V)4 resp. d-6 = (N/V)2 7

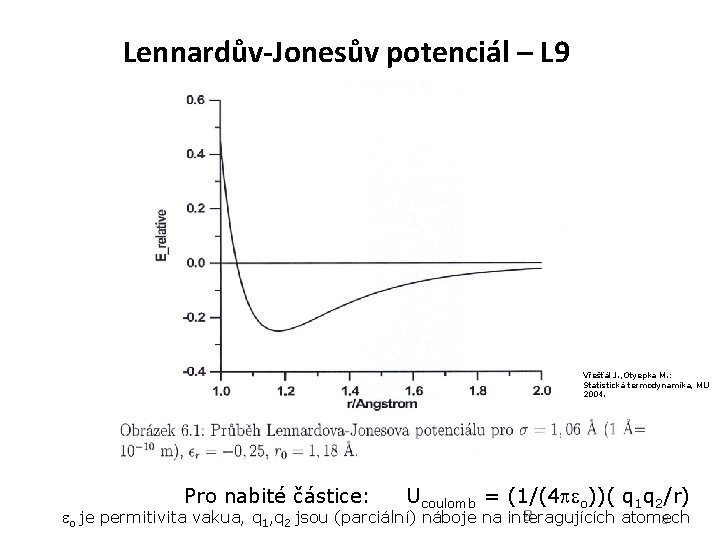
Lennardův-Jonesův potenciál – L 9 Vřešťál J. , Otyepka M. : Statistická termodynamika, MU 2004. Pro nabité částice: Ucoulomb = (1/(4 o))( q 1 q 2/r) 8 o je permitivita vakua, q 1, q 2 jsou (parciální) náboje na interagujících atomech 8

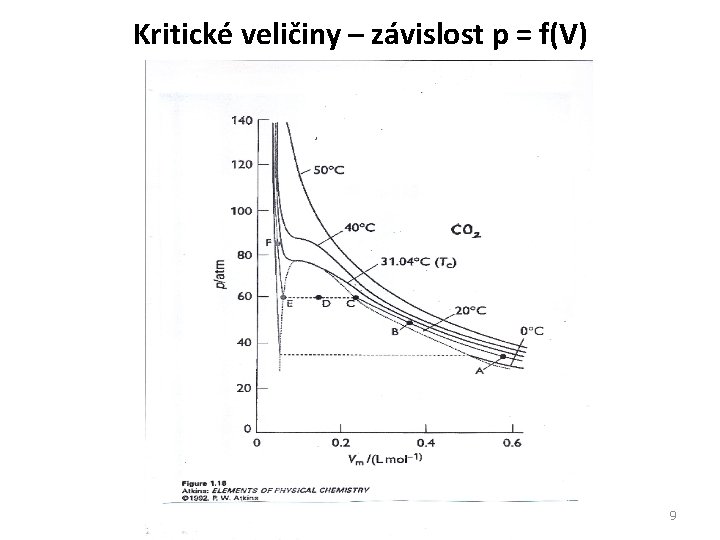
Kritické veličiny – závislost p = f(V) 9 9

Průměrná potenciální energie molekuly v buňce – pokračování Souřadnice minima L J potenciálové křivky u(r 0) a r 0 jsou úměrné kritickému objemu V* = N(r 0)3. Po úpravách dostaneme pro konfigurační integrál (konfigurační partiční funkci) pro jednu molekulu: qkonfig = 4 Pro migrující nerozlišitelné molekuly: celková partiční funkce souboru 10 Q konfig = (N qkonfig)N/ N!

Průměrná potenciální energie molekuly v buňce – pokračování Po úpravách: ln Q konfig = N[1 + ln(2 g(y)V/N) + [cu 0(ro)/k. T]((6/5)(V*/V)2 – ½(V*/V)4)] - konstanta – vliv geometrie buňky g(y) – funkce y = (r/a)2 c – geometrická konstanta (počet sousedů v buňce) 11 Fischer O. : Statistická termodynamika. UJEP Brno 1985

1. 2. Kritické veličiny Výpočet tlaku plynu N nerozlišitelných molekul s teplotou T: Q = Q konfig. /(N! 3 N) Platí vztah: p = k. T( ln. Qkonfig/ V)T, N (L 4/slide 19) • ( tepelná vlnová délka molekuly) Dosazení za Q konfig (slide 10) vede k závislosti tlaku p (p. V*/Nk. T) na objemu V (V/V*) při konstantní teplotě: p = k. T( N[1 + ln(2 g(y)V/N) + [cu 0(ro)/k. T]((6/5)(V*/V)2 – ½(V*/V)4)]/ V)T, N 12

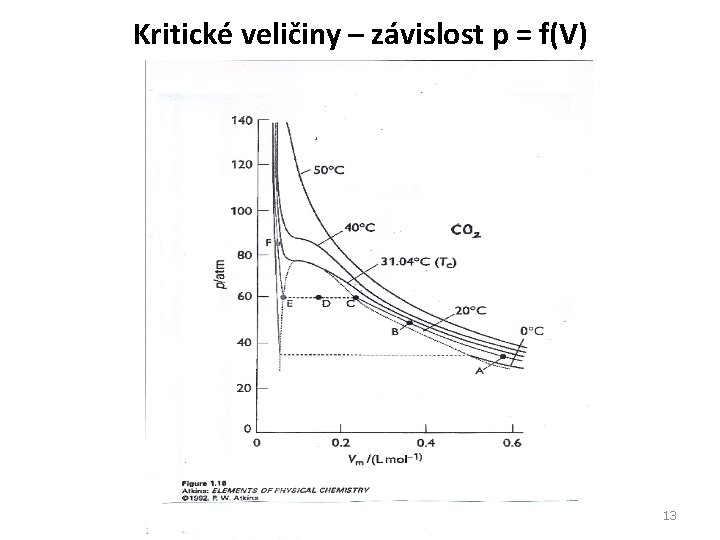
Kritické veličiny – závislost p = f(V) 13 13

Kritické veličiny - komentář Závislost tlaku p (p. V*/Nk. T) na objemu V (V/V*) při konstantní teplotě: Vyšší teploty: monotónně klesající průběh (Boyleův. Mariottův zákon) Nižší teploty: průběh s minimem (kondenzace) Teplota, pro kterou je na křivce inflexní bod: kritická teplota. (Shoda výpočtu s experimentem horší než 5%. ) Rychlá migrace molekul umožňuje přijmout předpoklad konstantního N i při nelokalizovaných molekulách. 14

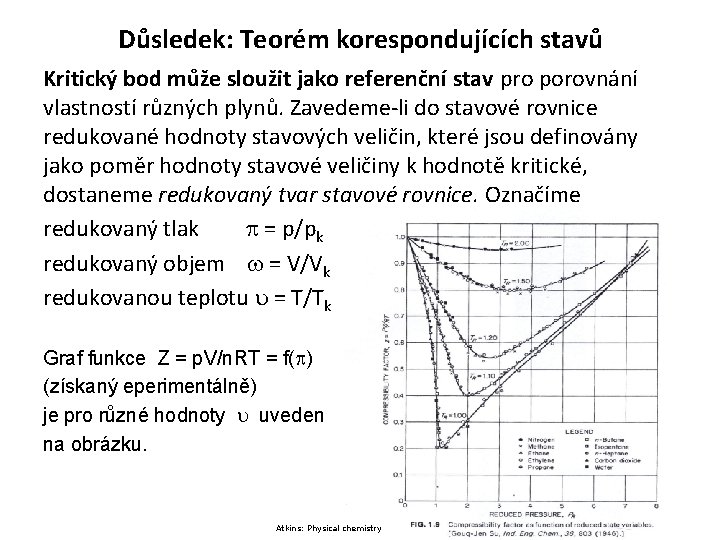
Důsledek: Teorém korespondujících stavů Kritický bod může sloužit jako referenční stav pro porovnání vlastností různých plynů. Zavedeme-li do stavové rovnice redukované hodnoty stavových veličin, které jsou definovány jako poměr hodnoty stavové veličiny k hodnotě kritické, dostaneme redukovaný tvar stavové rovnice. Označíme redukovaný tlak = p/pk , redukovaný objem = V/Vk , redukovanou teplotu = T/Tk Graf funkce Z = p. V/n. RT = f( ) (získaný eperimentálně) je pro různé hodnoty uveden na obrázku. Atkins: Physical chemistry 15

1. 3. Rovnováha kapalina - pára Pro ideální plyn platí (L 4): G = - k. T ln. Q a p. Vid=Nk. T Gid = -k. T ln. Qtransl + p. Vid = -Nk. T(-ln 3 + ln(k. T/P)). Pro kapaliny platí: Gkap = k. T ln(Qkonfig/ 3 N), (Qkonfig - slide 10) Porovnáním Gid = Gkap: ln P = ln (Nk. T/(2 g(y)Vkap) - 0/(k. T) - 1 ( -energie vypařování) 0 (P = C(T) exp(- Hv/RT) - Clausiova-Clapeyronova rovnice) 16

Rovnováha kapalina – pára - pokračování Pokračování: ln P = ln (Nk. T/(2 g(y)Vkap) - 0/(k. T) - 1 Numerické řešení pro výpočet tlaku souboru molekul P = (RT/2 g(y)Vkap) exp(-(N 0+RT)/(RT) vede k výrazu (cu 0 – slide 11): ln P = 1, 916 + ln(Ncu 0/V*) – 0, 678(cu 0/k. T) Tato rovnice je splněna, je-li Tvar/Tkrit 0, 6, kdy by mělo platit u 0 1, 25 k. Tvar Soulad vypočtené a experimentální Tvar se pohybuje v jednotkách K. Př. : H 20: Tvar = 373. 15 K, Tkrit = 647. 1 K……. Tvar/Tkrit = 0, 58 17

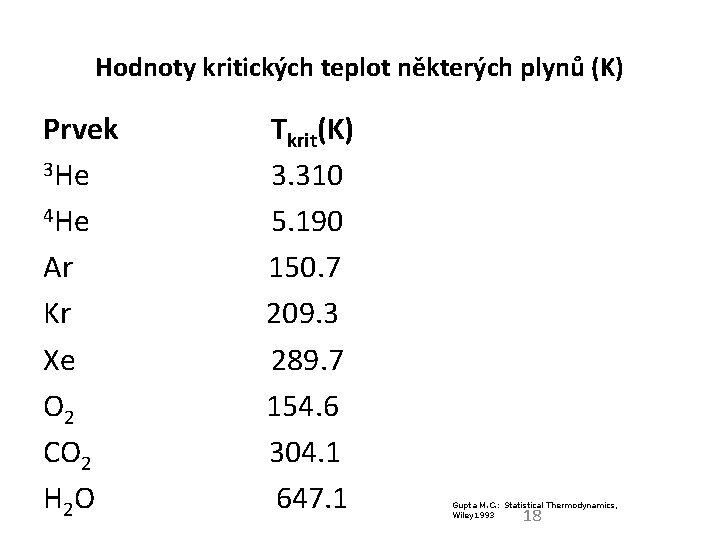
Hodnoty kritických teplot některých plynů (K) Prvek Tkrit(K) 3 He 3. 310 4 He 5. 190 Ar 150. 7 Kr 209. 3 Xe 289. 7 O 2 154. 6 CO 2 304. 1 H 2 O 647. 1 Gupta M. C. : Statistical Thermodynamics, Wiley 1993 18

Rovnováha kapalina – pára - pokračování Pro ( ln P/ T) = Hvyp/Nk. T 2 = 0, 678 cu 0/k. T 2 a odtud Troutonovo pravidlo (c=12): Hvyp/Tvar = 1, 25 Nkc 0, 678 = 84, 55 JK-1 mol-1 (Nk = R = 8. 314 J. K-1. mol-1) 19

2. Teorie volného objemu kapalin Definujeme konfigurační partiční funkci pro kapalinu s N molekulami: Qkonfig. = Vf. N exp(-Wm/RT) Vf je volný objem v kapalině v němž se pohybuje N molekul Wm potenciální energie 1 molu kapaliny (molární vnitřní energie vypařování) 20

Teorie volného objemu - pokračování Návaznost na buňkovou teorii: Uvnitř a vně buňky má molekula různé potenciální energie uint = Wm/N a uext = . Molekuly mohou (ale nemusejí) být lokalizovány do vlastního volného objemu. To umožňuje zjišťovat volný objem kapalin: - z geometrických úvah - z termodynamických dat (molární vnitřní energie vypařování) - z rychlosti šíření zvuku v kapalině a v jejich parách 21

Teorie volného objemu - pokračování Volný objem kapalin z rychlosti šíření zvuku v kapalině a v jejich parách Předpoklad: kolize částic při šíření zvuku – rychlý přenos jejich hybnosti pro poměr rychlosti šíření zvuku v kapalině ukap a v parách ug 1/3 lze psát: ukap/ ug = (Vm/Vf, m) Pro molární volný objem pak dostaneme: Vf, m = Vm/(ukap)3 (RT P/M)3/2, kde P je Poissonova konstanta ( P =Cp/CV) a M molární hmotnost. Příklad: Vypočtěte molární volný objem vody. 22

Příklad: Vypočtěte molární volný objem vody. Řešení: Vm = 18. 10 -6 m 3/mol ukap 1. 103 m/sec R = 8, 314 J/mol. K T = 298, 15 K M = 18. 10 -3 kg/mol P 1 Vf, m = Vm/(ukap)3 (RT P/M)3/2 (18. 10 -15)(1, 3. 105)3/2 = = (1, 8. 10 -14)(4, 7. 107) 8. 10 -7 m 3/mol (0. 8 cm 3/mol) 23

Vyjádření volného objemu pomocí tlaku Tlak lze vyjádřit jako p = k. T ( ln. Q/ V)T Volný molární vnitřní objem kapaliny: Vf, m = Vm ((b. RT)1/2/ Uvyp)3 b je geometrický faktor, pro kubickou kvazimřížku b = 2. (Postup je přibližný. ) Fischer O. : Statistická termodynamika. UJEP Brno 1985 24

Clausiova-Clapeyronova rovnice vyjádřená pomocí molárního volného objemu kapaliny a výparné vnitřní energie: P = RT/Vf, m exp(- Hvyp/RT) (Porovnejte s Clausiovou-Clapeyronovou rovnicí: P = C(T) exp(- Hv/RT) ve slidu 16 – buňková teorie. ) 25

3. Distribuční funkce Jednoatomové kapaliny: Centrální molekula má kulově symetrické potenciálové pole symetricky obsazené molekulami (v objemu V je N stejných molekul – buňková teorie). Celková potenciální energie souboru je W = N u(rij) (sečteno přes všech N molekul). Hledá se výraz pro pravděpodobnost umístění určitého počtu molekul v jednotlivých objemových elementech. 26

Distribučni funkce - pokračování Distribuční funkce n pro N nerozlišitelných molekul v n -objemových elementech v limitě představuje pravděpodobnost, že se všechny molekuly nacházejí ve sledovaném objemu V a je tedy rovna n-té mocnině molekulové hustoty N/V: lim n = (N/V)n W 0 27

Radiální distribuční (korelační) funkce (párová) gn: n = gn (N/V)n Např. : pro 2 molekuly: r 2 = (N/V)2 g(r 12), kde g(r 12) = N(N-1)/( 2 QNVT) … exp(-U(r 1…r. N)/k. T) dr 3…dr. N Radiální distribuční funkci lze graficky znázornit. 28

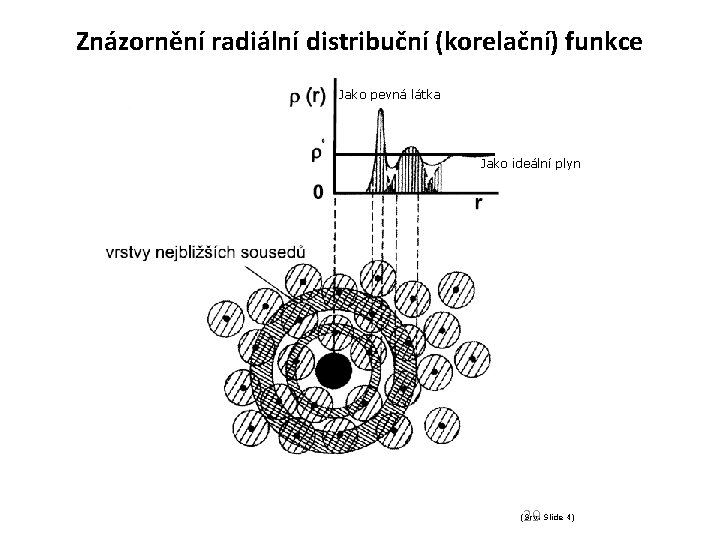
Znázornění radiální distribuční (korelační) funkce pro kapaliny Jako pevná látka Jako ideální plyn 29 (Srv. Slide 4)

Znázornění radiální distribuční (korelační) funkce komentář Komentář k obrázku: - v blízkosti středu molekuly klesá g(r) k nule - pak převládají přitažlivé síly a ve vzdálenosti prvního maxima se shromažďují okolní molekuly a tvoří vrstvu tzv. nejbližších sousedů (v systémech solut-solvent první solvatační sféru). Následuje zona repulse nejbližších sousedů a další vrstva (popř. další solvatační sféra). Funkce postupně „vyhasíná“. 30

Výpočet vnitřní energie kapalin U kapalin, na rozdíl od plynů, se budeme zabývat jen příspěvky externích modů pohybu a externích interakcí k vnitřní energii kapaliny (ne translace a rotace molekul). Bude platit: Qext = Qkonfig/(N! 3 N) (L 2, L 6) Konfigurační integrál (partiční funkci) Qkonfig (Qkf) vyjádříme pomocí radiální distribuční (korelační) funkce g(r) a potenciálové funkce u(r): 31

Výpočet vnitřní energie kapalin - pokračování Vnitřní energie spojená s externími mody pohybu je (L 4) Ze vztahu pro Qext = Qkonfig/(N! 3 N), dostaneme: kde W je příspěvek potenciální (interakční) energie párů molekul (párová distribuční funkce). 32 A. Malijevský: Skripta VŠCh. T Praha, 2008, str. 87

Viriální stavová rovnice je vyjádřením kompresibilitního faktoru reálného plynu Z: Z = PV/Nk. T = 1 + NB(T)/(NAV), kde B(T) je tzv. druhý viriální (viriálový) koeficient 33

Výpočet tlaku Pro vyjádření tlaku potřebujeme znát parciální derivaci partiční funkce Qext podle objemu: (L 4/slide 19) Q ext což umožňuje vyjádřit druhý viriální koeficient porovnáním s rozvojem pro kompresibilitní faktor reálného plynu: 34

Výpočet Helmholtzovy energie Pro soubor N nerozlišitelných molekul platí: Po úpravách dostaneme vztah pro chemický potenciál ve tvaru: jako funkci radiální distribuční funkce g(r) a potenciální energie u(r) molekul. (Zavedli jsme tzv. zapojovací koeficient , který charakterizuje zapojení molekul do vazeb a nabývá hodnoty od 0 do 1. ) 35

Doplněk: Jiné teorie Monte Carlo: rychlejší (zejména pro složitější molekuly), pouze termodynamické vlastnosti systému Molekulární dynamika: dynamické i termodynamické vlastnosti systému 36

Doplněk: Dvě a více složek v kapalině – mísení – L 12 Ideální roztok – platí odvozené vztahy, plus entropie mísení Neideální roztok: odmísení – odpudivé interakce složek A, B asociáty, clustery – přitažlivé interakce Teorie: kvazichemická – Guggenheim (1952) cluster variation method (CVM) – Kikuchi (1951) 37

Doplněk: aktivita modů pohybu 38

Shrnutí poznatků Buňková teorie kapalin – partiční funkce: Q konfig = (N qkonfig)N/ N! ln Q konfig = N[1 + ln(2 g(y)V/N) + [cu 0(r)/k. T]((6/5)(V*/V)2 – ½(V*/V)4)] Kritické veličiny Teorie volného objemu: Vf, m = Vm/(ukap)3 (RT P/M)3/2, Hvyp/Tvar = 1, 25 Nkc 0, 678 84, 5 JK-1 mol-1 Troutonovo pravidlo Radiální korelační (distribuční) funkce – solvatační sféra – graf g(r 12) = N(N-1)/( 2 QNVT) … exp(-U(r 1…r. N)/k. T) dr 3…dr. N Vnitřní energie kapalin W – interakční energie párů 39