Vectors geometry Playing with arrows How using a

Vectors geometry: Playing with arrows • How using a vector (arrow) we can represent concepts of – Mean, variance (standard deviation), normalization and standardization. • How using two vectors we can represent concepts of – Correlation and regression.

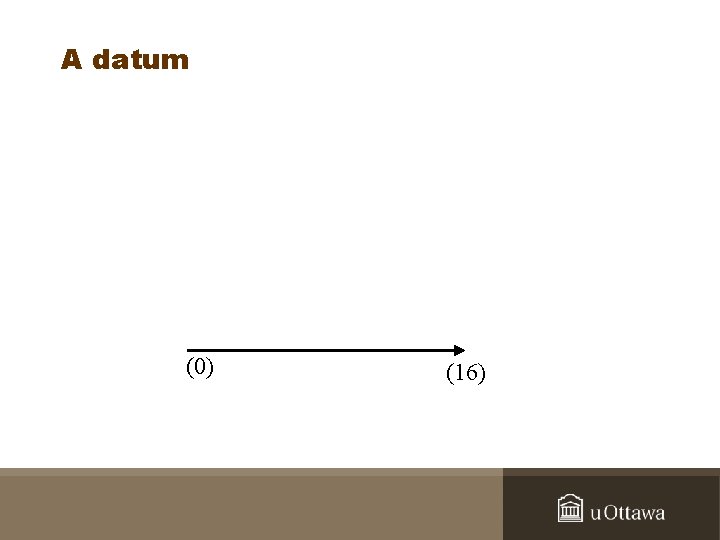
A datum (0) (16)

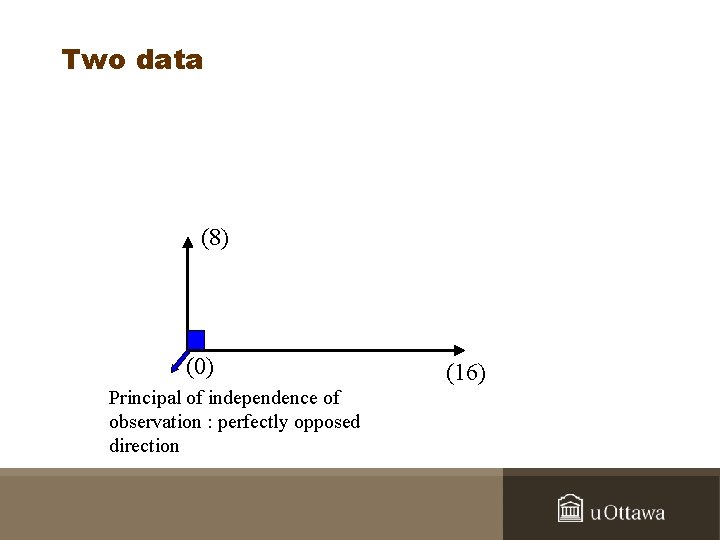
Two data (8) (0) Principal of independence of observation : perfectly opposed direction (16)

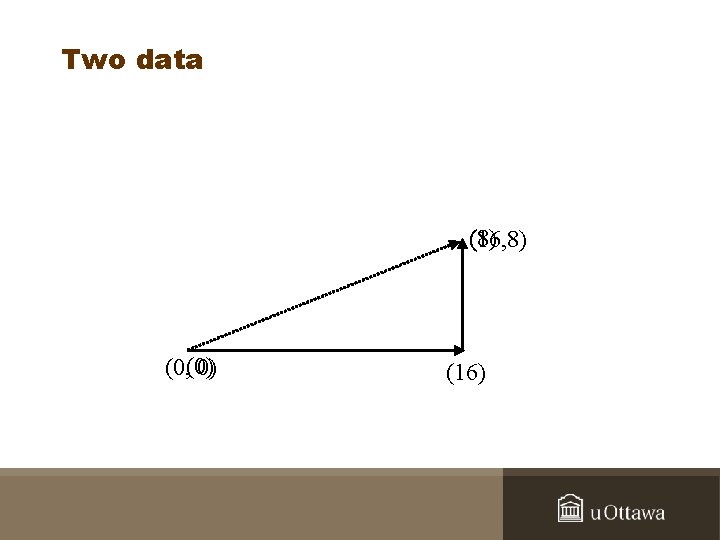
Two data (8) (16, 8) (0, (0) 0) (16)

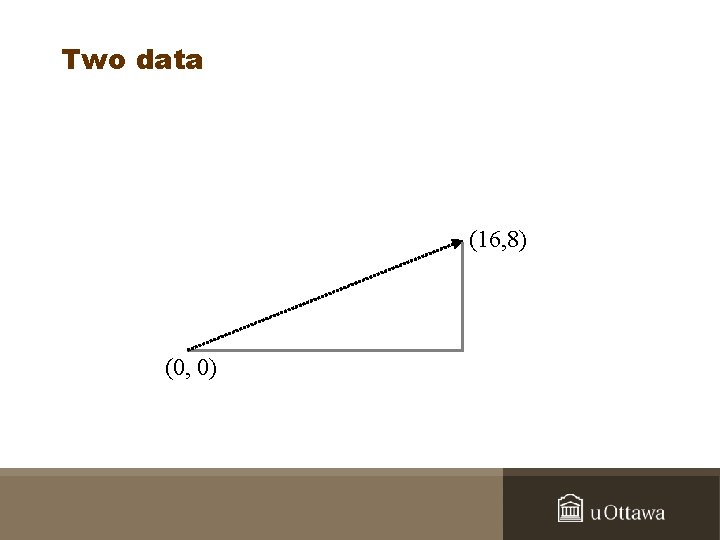
Two data (16, 8) (0, 0)

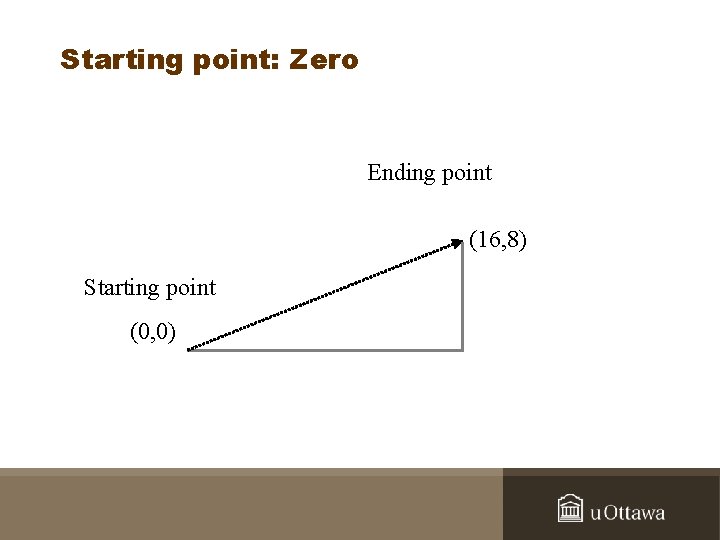
Starting point: Zero Ending point (16, 8) Starting point (0, 0)

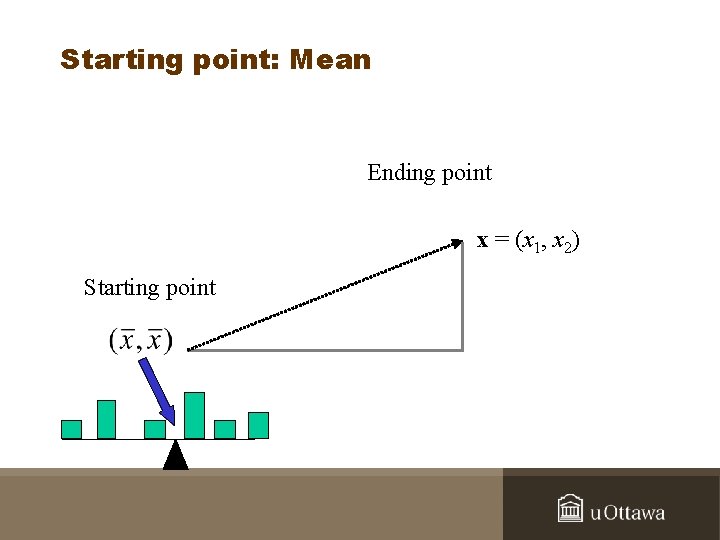
Starting point: Mean Ending point x = (x 1, x 2) Starting point

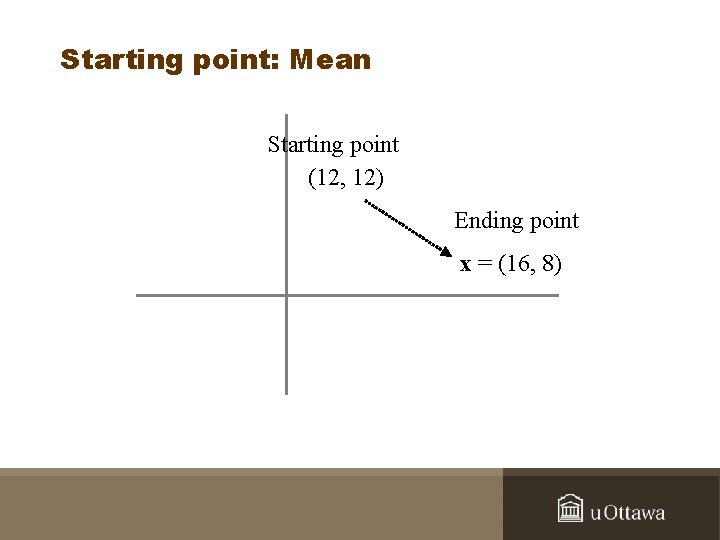
Starting point: Mean Starting point (12, 12) Ending point x = (16, 8)

One group

Many groups

Degrees of freedom

We removed the effect of the mean We centralized the data Starting point (mean) (12, 12) (0, 0) Ending point x = (16, 8) = (4, -4)

We removed the effect of the mean (many groups)

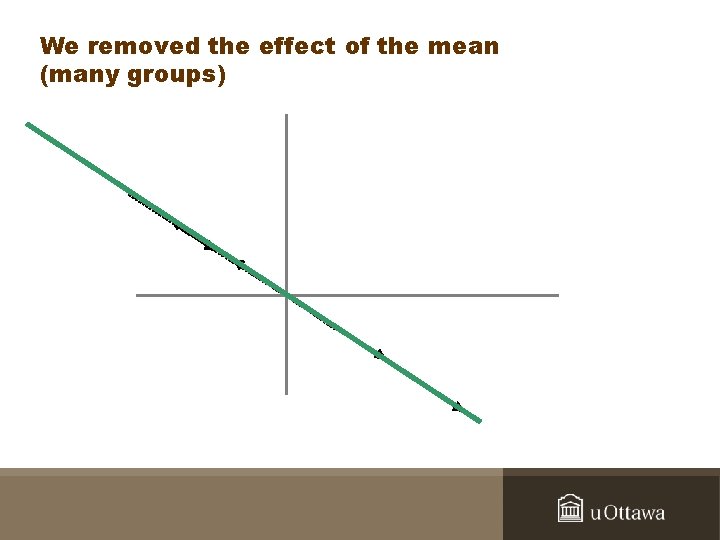
We removed the effect of the mean (many groups)

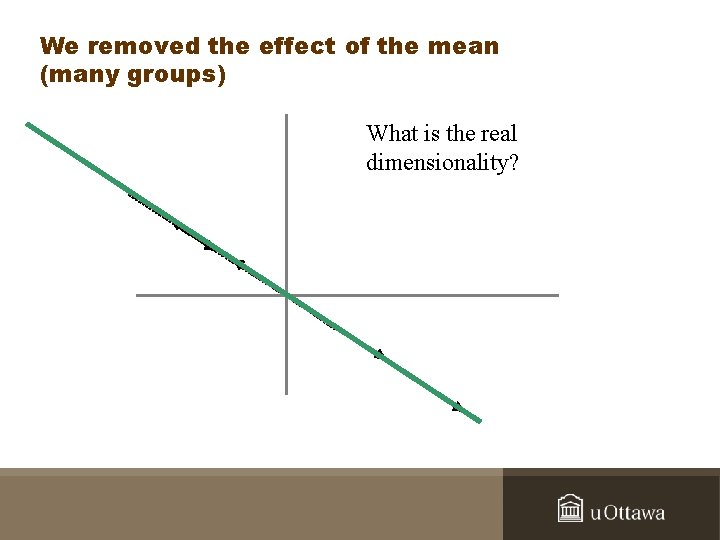
We removed the effect of the mean (many groups) What is the real dimensionality?

We removed the effect of the man • If we have two data, we will get one dimension. • If we have three data, we will get two dimensions. . . • If we have n data, we will get n-1 dimensions. Ø In other words, degrees of freedom represent the true dimensionality of the data.

Variance

What is the difference between these three vectors (composed of two data each) ? Ø Length (distance) Ø The higher the variability, the longer the length will be. (-0. 5, 0, 5) (1. 5, -1. 5) (2. 5, -2. 5)

What is the difference between these three arrows? How do we measure the length (distance)? ØPythagoras ØHypotenuse of a triangle Ø? = (4^2+3^2) = 25 = 5 (4, 3) 5? 3 4

What is the difference between these three arrows? Therefore, the point (4, 3) is at a distance of 5 from its starting point. = sum of squares = variance×(n-1) (4, 3) 5

What is the difference between these three arrows? What is the length of these three lines? 1? A) 1 1 1 2? B) C) 3 ? 1 1 1 Ø The dimensionality inflates the variability. ØIn order to a have a measure that can take into account the dimensionality, what do we need to do?

What is the difference between these three arrows? • We divide the length of the data set by its true dimensionality = (quadratic) distance (from the mean) corrected by the (true) dimensionality of the data.

Normalization et standardization

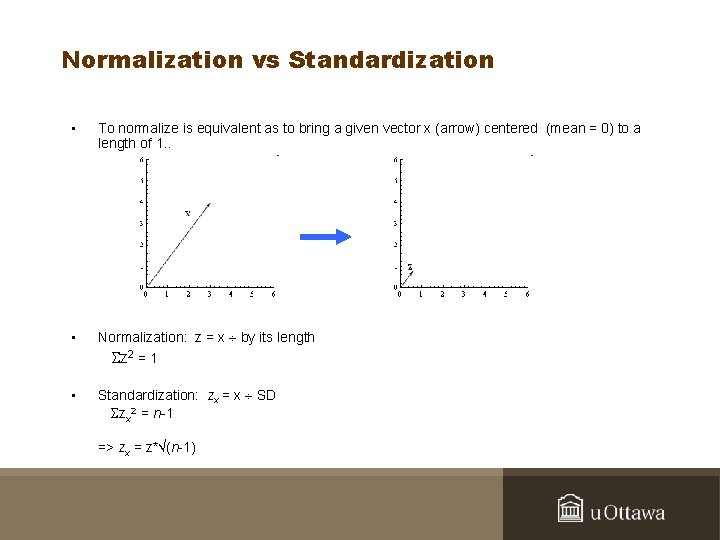
Normalization vs Standardization • To normalize is equivalent as to bring a given vector x (arrow) centered (mean = 0) to a length of 1. . • Normalization: z = x by its length Sz 2 = 1 • Standardization: zx = x SD Szx 2 = n-1 => zx = z* (n-1)

Two groups or two variables

One group of three participants

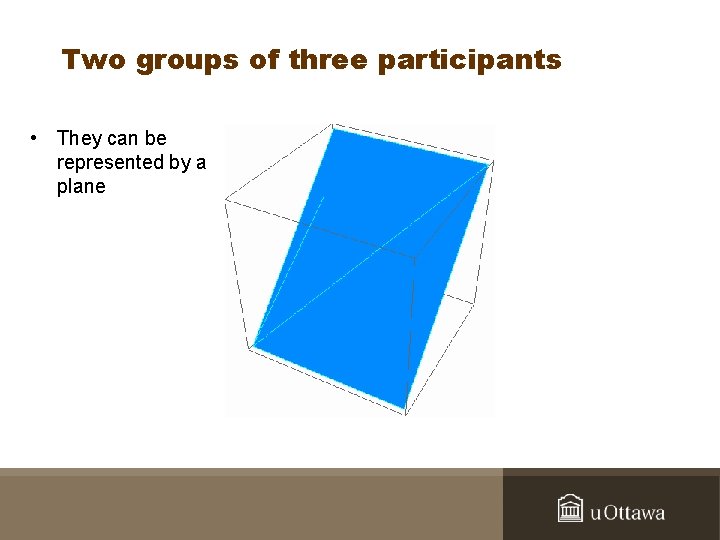
Two groups of three participants

Two groups of three participants • They can be represented by a plane

Two groups of three participants • They can be represented by a plane

Two groups of three participants • They can be represented by a plane

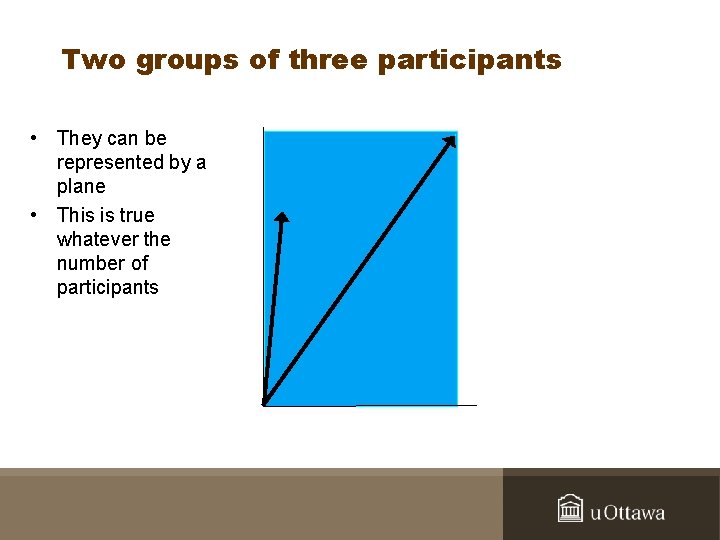
Two groups of three participants • They can be represented by a plane • This is true whatever the number of participants

Correlation and regression

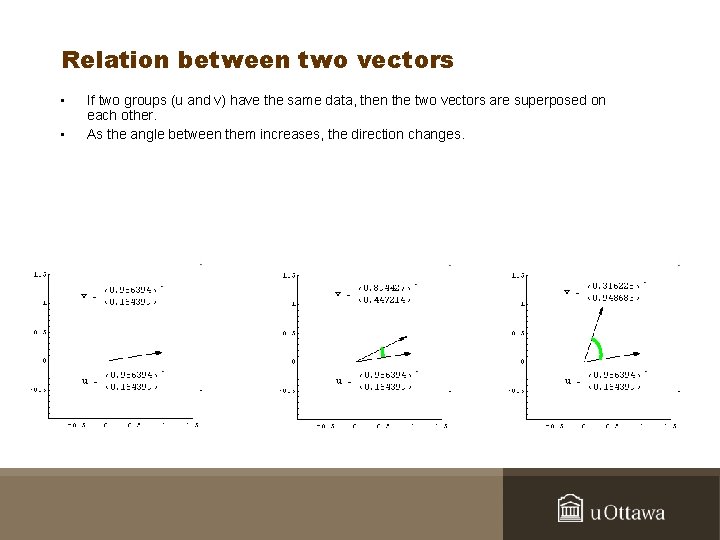
Relation between two vectors • • If two groups (u and v) have the same data, then the two vectors are superposed on each other. As the angle between them increases, the direction changes.

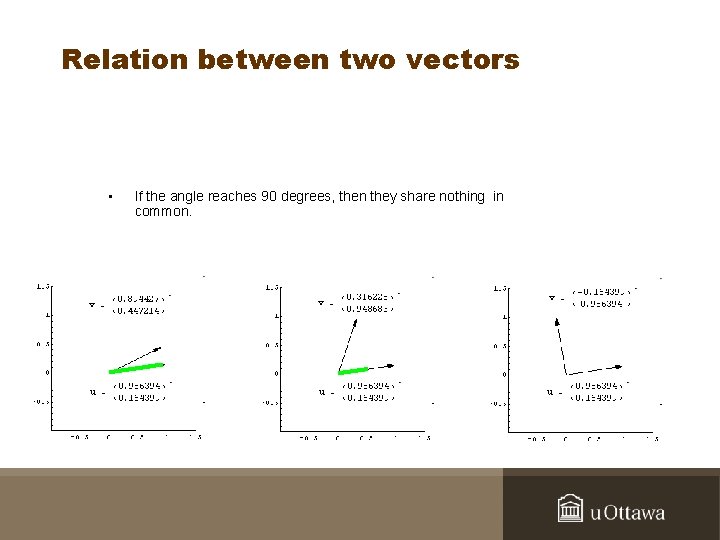
Relation between two vectors • If the angle reaches 90 degrees, then they share nothing in common.

Relation between two vectors • The cosine of the angle is the coefficient of correlation