12 VECTORS AND THE GEOMETRY OF SPACE VECTORS























































- Slides: 65

12 VECTORS AND THE GEOMETRY OF SPACE

VECTORS AND THE GEOMETRY OF SPACE In this chapter, we introduce vectors and coordinate systems for three-dimensional space.

VECTORS AND THE GEOMETRY OF SPACE This will be the setting for our study of the calculus of functions of two variables in Chapter 14. § This is because the graph of such a function is a surface in space.

VECTORS AND THE GEOMETRY OF SPACE We will see that vectors provide particularly simple descriptions of lines and planes in space.

VECTORS AND THE GEOMETRY OF SPACE 12. 1 Three-Dimensional Coordinate Systems In this section, we will learn about: Aspects of three-dimensional coordinate systems.

TWO-DIMENSIONAL (2 -D) COORDINATE SYSTEMS To locate a point in a plane, two numbers are necessary. § We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers—where a is the x-coordinate and b is the y-coordinate. § For this reason, a plane is called two-dimensional.

THREE-DIMENSIONAL (3 -D) COORDINATE SYSTEMS To locate a point in space, three numbers are required. § We represent any point in space by an ordered triple (a, b, c) of real numbers.

3 -D COORDINATE SYSTEMS In order to represent points in space, we first choose: § A fixed point O (the origin) § Three directed lines through O that are perpendicular to each other

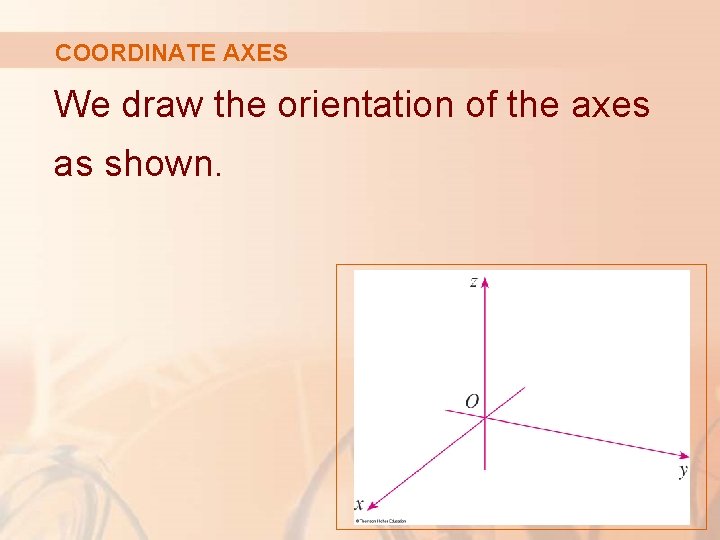
COORDINATE AXES The three lines are called the coordinate axes. They are labeled: § x-axis § y-axis § z-axis

COORDINATE AXES Usually, we think of: § The x- and y-axes as being horizontal § The z-axis as being vertical

COORDINATE AXES We draw the orientation of the axes as shown.

COORDINATE AXES The direction of the z-axis is determined by the right-hand rule, illustrated as follows.

COORDINATE AXES Curl the fingers of your right hand around the z-axis in the direction of a 90° counterclockwise rotation from the positive x-axis to the positive y-axis. § Then, your thumb points in the positive direction of the z-axis.

COORDINATE PLANES The three coordinate axes determine three coordinate planes. § The xy-plane contains the x- and y-axes. § The yz-plane contains the y- and z-axes. § The xz-plane contains the x- and z-axes.

OCTANTS These three coordinate planes divide space into eight parts, called octants. § The first octant, in the foreground, is determined by the positive axes.

3 -D COORDINATE SYSTEMS Many people have some difficulty visualizing diagrams of 3 -D figures. Thus, you may find it helpful to do the following.

3 -D COORDINATE SYSTEMS Look at any bottom corner of a room and call the corner the origin.

3 -D COORDINATE SYSTEMS The wall on your left is in the xz-plane. The wall on your right is in the yz-plane. The floor is in the xy-plane.

3 -D COORDINATE SYSTEMS The x-axis runs along the intersection of the floor and the left wall. The y-axis runs along that of the floor and the right wall.

3 -D COORDINATE SYSTEMS The z-axis runs up from the floor toward the ceiling along the intersection of the two walls.

3 -D COORDINATE SYSTEMS You are situated in the first octant. You can now imagine seven other rooms situated in the other seven octants. § There are three on the same floor and four on the floor below. § They are all connected by the common corner point O.

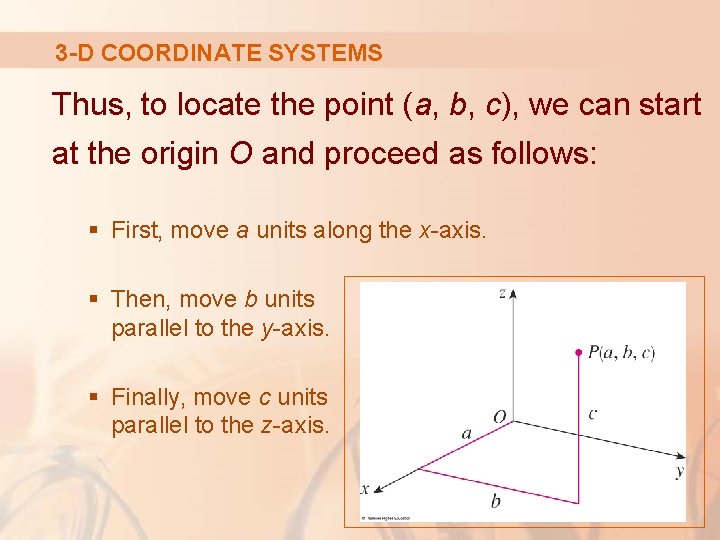
3 -D COORDINATE SYSTEMS Now, if P is any point in space, let: § a be the (directed) distance from the yz-plane to P. § b be the distance from the xz-plane to P. § c be the distance from the xy-plane to P.

3 -D COORDINATE SYSTEMS We represent the point P by the ordered triple of real numbers (a, b, c). We call a, b, and c the coordinates of P. § a is the x-coordinate. § b is the y-coordinate. § c is the z-coordinate.

3 -D COORDINATE SYSTEMS Thus, to locate the point (a, b, c), we can start at the origin O and proceed as follows: § First, move a units along the x-axis. § Then, move b units parallel to the y-axis. § Finally, move c units parallel to the z-axis.

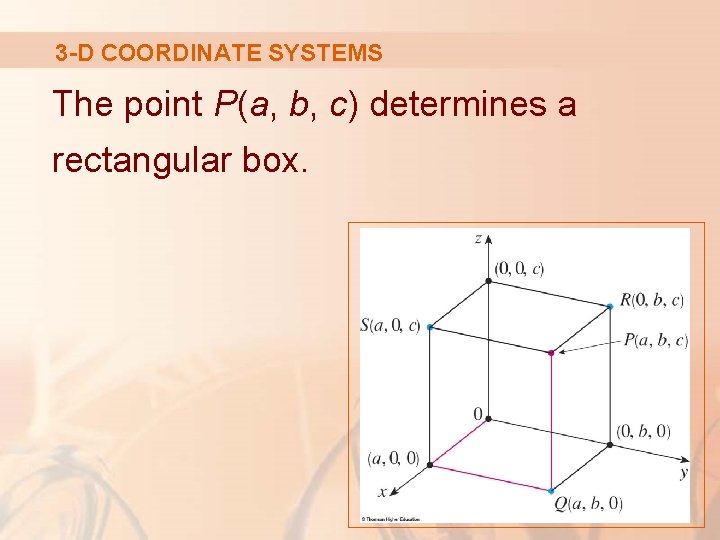
3 -D COORDINATE SYSTEMS The point P(a, b, c) determines a rectangular box.

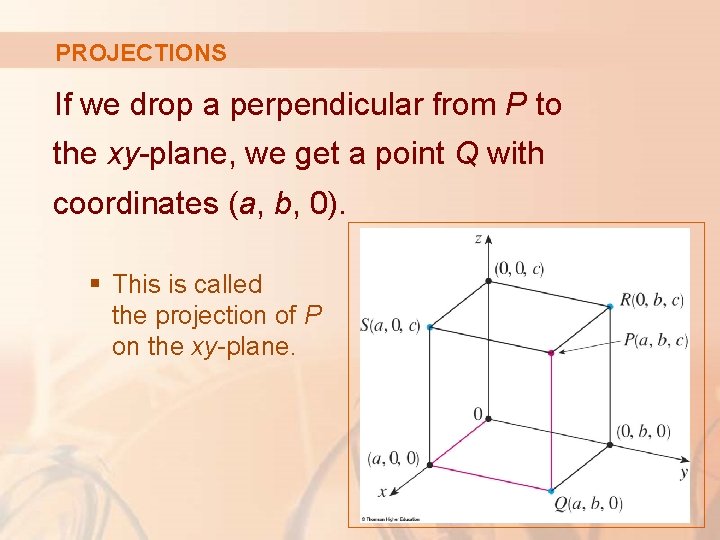
PROJECTIONS If we drop a perpendicular from P to the xy-plane, we get a point Q with coordinates (a, b, 0). § This is called the projection of P on the xy-plane.

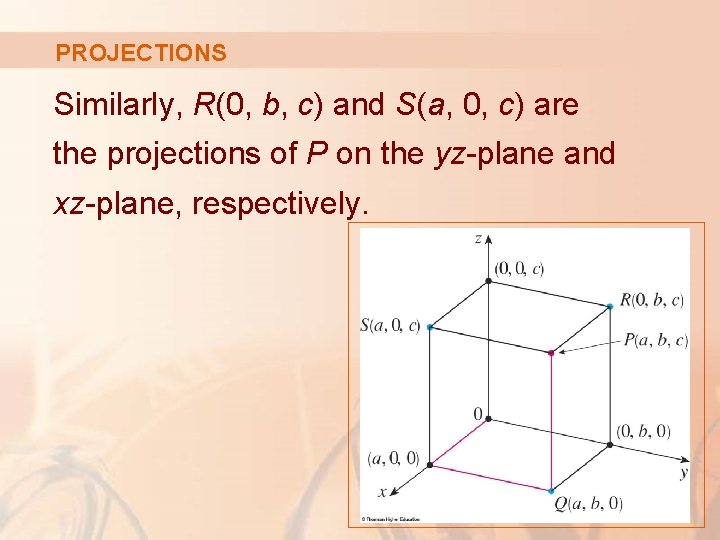
PROJECTIONS Similarly, R(0, b, c) and S(a, 0, c) are the projections of P on the yz-plane and xz-plane, respectively.

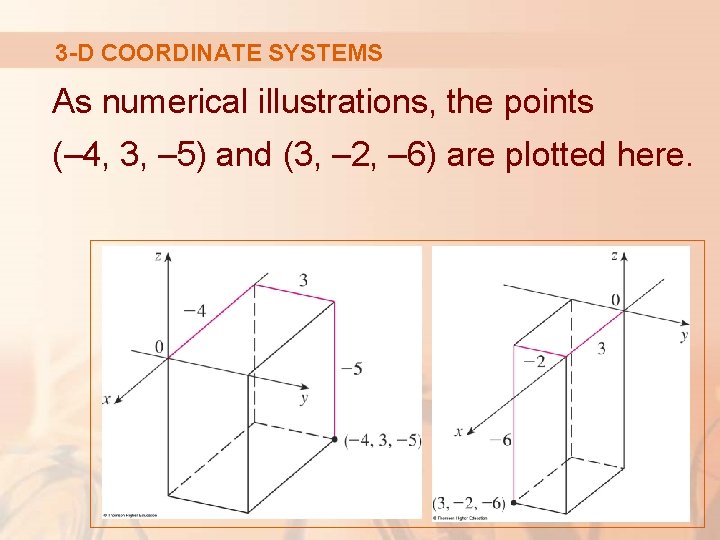
3 -D COORDINATE SYSTEMS As numerical illustrations, the points (– 4, 3, – 5) and (3, – 2, – 6) are plotted here.

3 -D COORDINATE SYSTEMS The Cartesian product R x R = {(x, y, z) | x, y, z R} is the set of all ordered triples of real numbers and is denoted by R 3.

3 -D RECTANGULAR COORDINATE SYSTEM We have given a one-to-one correspondence between points P in space and ordered triples (a, b, c) in R 3. § It is called a 3 -D rectangular coordinate system.

3 -D RECTANGULAR COORDINATE SYSTEM Notice that, in terms of coordinates, the first octant can be described as the set of points whose coordinates are all positive.

2 -D VS. 3 -D ANALYTIC GEOMETRY In 2 -D analytic geometry, the graph of an equation involving x and y is a curve in R 2. In 3 -D analytic geometry, an equation in x, y, and z represents a surface in R 3.

3 -D COORDINATE SYSTEMS Example 1 What surfaces in R 3 are represented by the following equations? a. z = 3 b. y = 5

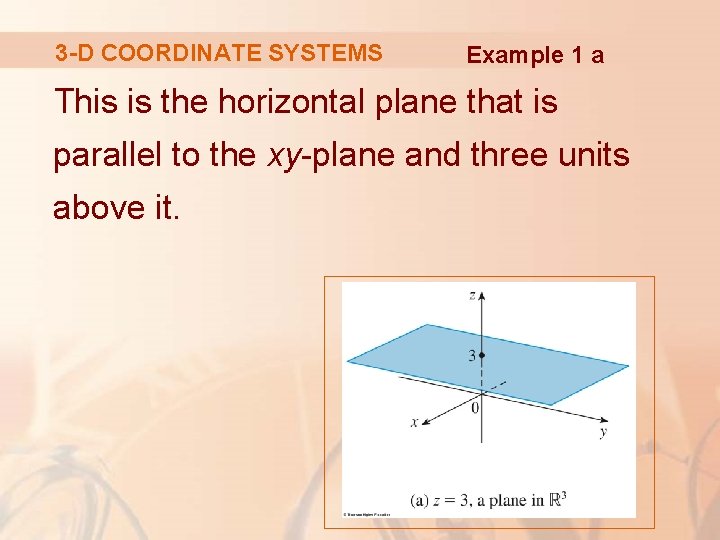
3 -D COORDINATE SYSTEMS Example 1 a The equation z = 3 represents the set {(x, y, z) | z = 3}. § This is the set of all points in R 3 whose z-coordinate is 3.

3 -D COORDINATE SYSTEMS Example 1 a This is the horizontal plane that is parallel to the xy-plane and three units above it.

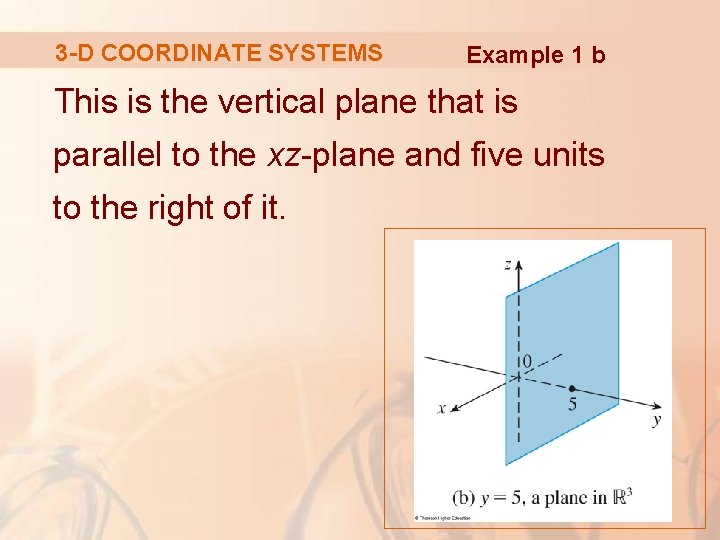
3 -D COORDINATE SYSTEMS Example 1 b The equation y = 5 represents the set of all points in R 3 whose y-coordinate is 5.

3 -D COORDINATE SYSTEMS Example 1 b This is the vertical plane that is parallel to the xz-plane and five units to the right of it.

NOTE Note When an equation is given, we must understand from the context whether it represents either: § A curve in R 2 § A surface in R 3

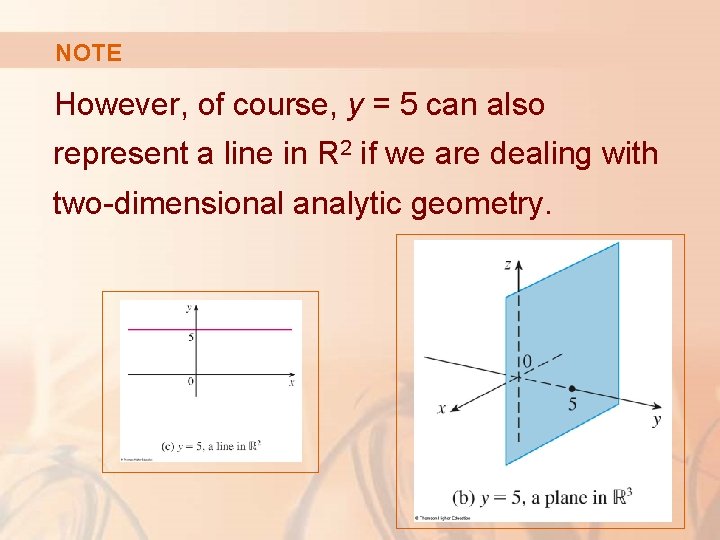
NOTE In Example 1, y = 5 represents a plane in R 3.

NOTE However, of course, y = 5 can also represent a line in R 2 if we are dealing with two-dimensional analytic geometry.

NOTE In general, if k is a constant, then § x = k represents a plane parallel to the yz-plane. § y = k is a plane parallel to the xz-plane. § z = k is a plane parallel to the xy-plane.

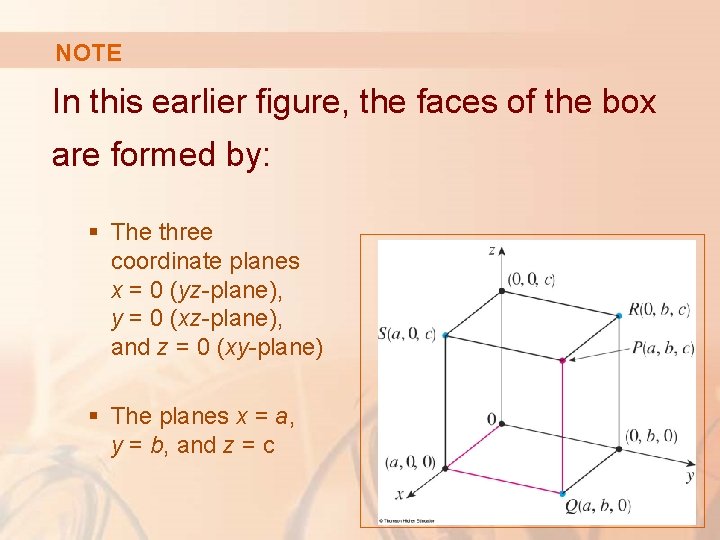
NOTE In this earlier figure, the faces of the box are formed by: § The three coordinate planes x = 0 (yz-plane), y = 0 (xz-plane), and z = 0 (xy-plane) § The planes x = a, y = b, and z = c

3 -D COORDINATE SYSTEMS Example 2 Describe and sketch the surface in R 3 represented by the equation y=x

3 -D COORDINATE SYSTEMS Example 2 The equation represents the set of all points in R 3 whose x- and y-coordinates are equal, that is, {(x, x, z) | x R, z R}. § This is a vertical plane that intersects the xy-plane in the line y = x, z = 0.

3 -D COORDINATE SYSTEMS Example 2 The portion of this plane that lies in the first octant is sketched here.

3 -D COORDINATE SYSTEMS The familiar formula for the distance between two points in a plane is easily extended to the following 3 -D formula.

DISTANCE FORMULA IN THREE DIMENSIONS The distance |P 1 P 2| between the points P 1(x 1, y 1, z 1) and P 2(x 2, y 2, z 2) is:

3 -D COORDINATE SYSTEMS To see why this formula is true, we construct a rectangular box as shown, where: § P 1 and P 2 are opposite vertices. § The faces of the box are parallel to the coordinate planes.

3 -D COORDINATE SYSTEMS If A(x 2, y 1, z 1) and B(x 2, y 2, z 1) are the vertices of the box, then § |P 1 A| = |x 2 – x 1| § |AB| = |y 2 – y 1| § |BP 2| = |z 2 – z 1|

3 -D COORDINATE SYSTEMS Triangles P 1 BP 2 and P 1 AB are right-angled. So, two applications of the Pythagorean Theorem give: § |P 1 P 2|2 = |P 1 B|2 + |BP 2|2 § |P 1 B|2 = |P 1 A|2 + |AB|2

3 -D COORDINATE SYSTEMS Combining those equations, we get: |P 1 P 2|2 = |P 1 A|2 + |AB|2 + |BP 2|2 = |x 2 – x 1|2 + |y 2 – y 1|2 + |z 2 – z 1|2 = (x 2 – x 1)2 + (y 2 – y 1)2 + (z 2 – z 1)2

3 -D COORDINATE SYSTEMS Therefore,

3 -D COORDINATE SYSTEMS Example 3 The distance from the point P(2, – 1, 7) to the point Q(1, – 3, 5) is:

3 -D COORDINATE SYSTEMS Example 4 Find an equation of a sphere with radius r and center C(h, k, l).

3 -D COORDINATE SYSTEMS Example 4 By definition, a sphere is the set of all points P(x, y , z) whose distance from C is r.

3 -D COORDINATE SYSTEMS Example 4 Thus, P is on the sphere if and only if |PC| = r § Squaring both sides, we have |PC|2 = r 2 or (x – h)2 + (y – k)2 + (z – l)2 = r 2

3 -D COORDINATE SYSTEMS The result of Example 4 is worth remembering. § We write it as follows.

EQUATION OF A SPHERE An equation of a sphere with center C(h, k, l) and radius r is: (x – h)2 + (y – k)2 + (z – l)2 = r 2 § In particular, if the center is the origin O, then an equation of the sphere is: x 2 + y 2 + z 2 = r 2

3 -D COORDINATE SYSTEMS Example 5 Show that x 2 + y 2 + z 2 + 4 x – 6 y + 2 z + 6 = 0 is the equation of a sphere. Also, find its center and radius.

3 -D COORDINATE SYSTEMS Example 5 We can rewrite the equation in the form of an equation of a sphere if we complete squares: (x 2 + 4 x + 4) + (y 2 – 6 y + 9) + (z 2 + 2 z + 1) = – 6 + 4 + 9 + 1 (x + 2)2 + (y – 3)2 + (z + 1)2 = 8

3 -D COORDINATE SYSTEMS Example 5 Comparing this equation with the standard form, we see that it is the equation of a sphere with center (– 2, 3, – 1) and radius

3 -D COORDINATE SYSTEMS Example 6 What region in R 3 is represented by the following inequalities? 1 ≤ x 2 + y 2 + z 2 ≤ 4 z≤ 0

3 -D COORDINATE SYSTEMS Example 6 The inequalities 1 ≤ x 2 + y 2 + z 2 ≤ 4 can be rewritten as: § So, they represent the points (x, y, z) whose distance from the origin is at least 1 and at most 2.

3 -D COORDINATE SYSTEMS Example 6 However, we are also given that z ≤ 0. § So, the points lie on or below the xy-plane.

3 -D COORDINATE SYSTEMS Example 6 Thus, the given inequalities represent the region that lies: § Between (or on) the spheres x 2 + y 2 + z 2 = 1 and x 2 + y 2 + z 2 = 4 § Beneath (or on) the xy-plane
 Vectors and the geometry of space
Vectors and the geometry of space Dot product
Dot product Chapter 12 vectors and the geometry of space
Chapter 12 vectors and the geometry of space Dot product
Dot product Scalar triple product properties
Scalar triple product properties Dot product
Dot product Electron geometry and molecular geometry
Electron geometry and molecular geometry 4 electron domains 2 lone pairs
4 electron domains 2 lone pairs Bonding theories
Bonding theories Cartesian space trajectory planning
Cartesian space trajectory planning Space junk the space age began
Space junk the space age began Camera space to world space
Camera space to world space Cartesian space vs joint space
Cartesian space vs joint space World space to screen space
World space to screen space Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Gấu đi như thế nào
Gấu đi như thế nào Tư thế worm breton
Tư thế worm breton Hát lên người ơi alleluia
Hát lên người ơi alleluia Môn thể thao bắt đầu bằng từ chạy
Môn thể thao bắt đầu bằng từ chạy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Phép trừ bù
Phép trừ bù độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế
Cái miệng nó xinh thế Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Ví dụ giọng cùng tên
Ví dụ giọng cùng tên Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể So nguyen to
So nguyen to Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Hổ sinh sản vào mùa nào
Hổ sinh sản vào mùa nào Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Sơ đồ cơ thể người
Sơ đồ cơ thể người Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi The multimodal text big ed mona
The multimodal text big ed mona Line segment geometry
Line segment geometry Vectors and scalars in physics
Vectors and scalars in physics What are i and j in vectors
What are i and j in vectors Vector scalar multiplication
Vector scalar multiplication A vector has both a magnitude and a
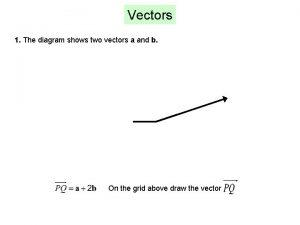
A vector has both a magnitude and a The diagram shows a regular hexagon and a parallelogram
The diagram shows a regular hexagon and a parallelogram Two dimensional motion and vectors
Two dimensional motion and vectors What are scalar and vector quantities
What are scalar and vector quantities Scalars and vectors
Scalars and vectors