VECTORES EN EL PLANO Magnitudes escalares y vectoriales

VECTORES EN EL PLANO

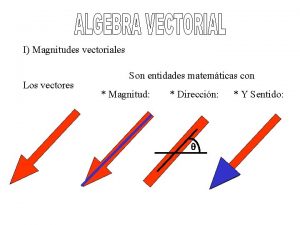
Magnitudes escalares y vectoriales ¿Cuánto vale una camisa? ¿Qué grosor tiene un cristal? ¿Cuál es la altura de un niño? ¿Qué capacidad tiene una jarra? Todas estas preguntas tienen por respuesta un número y una unidad de medida. Sin embargo, si hablamos del viento no basta con una cantidad que exprese su intensidad, necesitamos su dirección y su sentido. Estamos ante dos tipos de magnitudes: • Las magnitudes escalares, para cuya determinación se necesita un número que exprese su medida. • Las magnitudes vectoriales, como la velocidad de un móvil, el viento, la fuerza, la gravedad, …, que necesitan determinar su intensidad, dirección y sentido.

VECTORES EN EL PLANO • VECTOR FIJO • VECTORES EQUIPOLENTES • COMPONENTES DE UN VECTOR • VECTOR LIBRE • SUMA DE VECTORES LIBRES • PRODUCTO DE UN VECTOR POR UN ESCALAR

Vectores en el plano • vector fijo de origen A y extremo B, al segmento orientado que va A Llamaremos de A a B. Lo indicaremos con • Llamaremos módulo del vector π a la longitud del segmento AB. • Su dirección será la de la recta determinada por los puntos A y B. • Su sentido es el que va de A a B. • Diremos que dos vectores son equipolentes (equivalentes) si tienen el mismo módulo dirección y sentido B

Componentes de un vector Llamamos COMPONENTES de un vector al par de números reales . B =(b 1, b 2) v 2 =(b 2 – a 2) A =(a 1, a 2) . Dado el vector fijo , hallamos sus componentes restando las coordenadas del origen a las del extremo v 1 =(b 1 - a 1) Si A =(-2, 2) y B =(3, -1), las componentes del vector serán: A =(-2, 2) B =(3, -1)

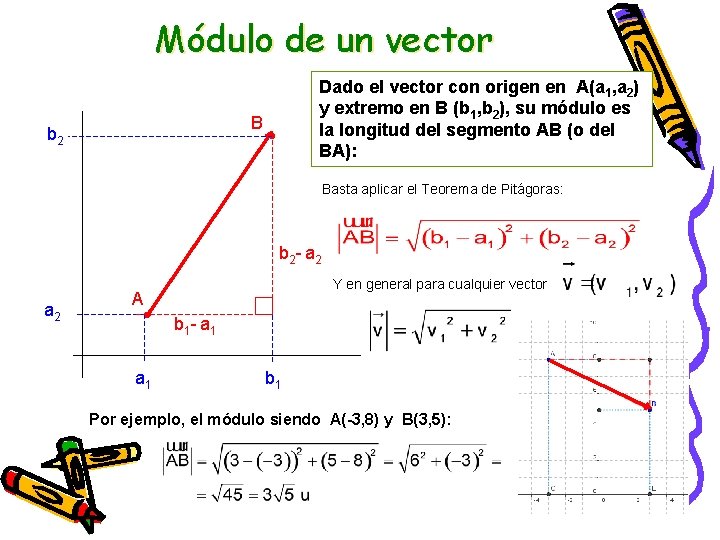
Módulo de un vector Dado el vector con origen en A(a 1, a 2) y extremo en B (b 1, b 2), su módulo es la longitud del segmento AB (o del BA): B b 2 Basta aplicar el Teorema de Pitágoras: b 2 - a 2 Y en general para cualquier vector A b 1 - a 1 b 1 Por ejemplo, el módulo siendo A(-3, 8) y B(3, 5):

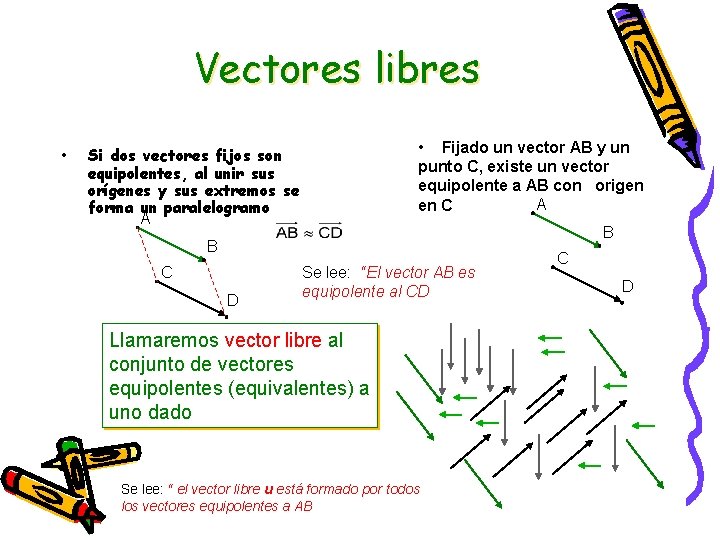
Vectores libres • • Fijado un vector AB y un punto C, existe un vector equipolente a AB con origen A en C Si dos vectores fijos son equipolentes, al unir sus orígenes y sus extremos se forma un paralelogramo A B B C D Se lee: “El vector AB es equipolente al CD Llamaremos vector libre al conjunto de vectores equipolentes (equivalentes) a uno dado Se lee: “ el vector libre u está formado por todos los vectores equipolentes a AB C D

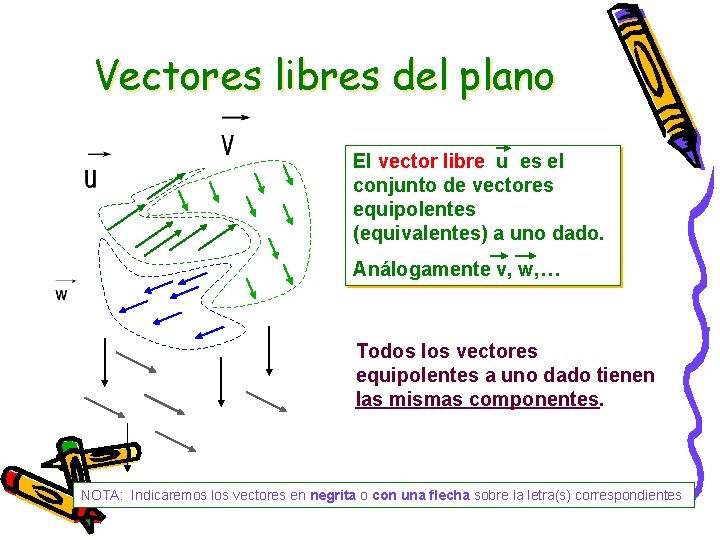
Vectores libres del plano El vector libre u es el conjunto de vectores equipolentes (equivalentes) a uno dado. Análogamente v, w, … Todos los vectores equipolentes a uno dado tienen las mismas componentes. NOTA: Indicaremos los vectores en negrita o con una flecha sobre la letra(s) correspondientes

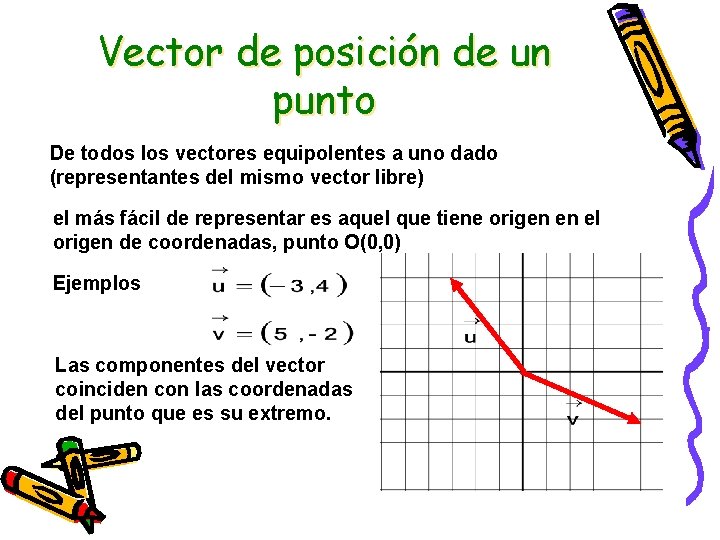
Vector de posición de un punto De todos los vectores equipolentes a uno dado (representantes del mismo vector libre) el más fácil de representar es aquel que tiene origen en el origen de coordenadas, punto O(0, 0) Ejemplos Las componentes del vector coinciden con las coordenadas del punto que es su extremo.

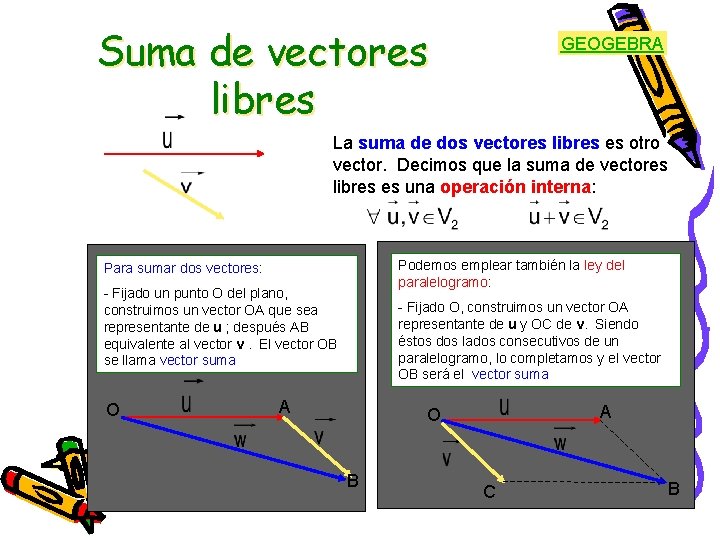
Suma de vectores libres GEOGEBRA La suma de dos vectores libres es otro vector. Decimos que la suma de vectores libres es una operación interna: Podemos emplear también la ley del paralelogramo: Para sumar dos vectores: - Fijado un punto O del plano, construimos un vector OA que sea representante de u ; después AB equivalente al vector v. El vector OB se llama vector suma O - Fijado O, construimos un vector OA representante de u y OC de v. Siendo éstos dos lados consecutivos de un paralelogramo, lo completamos y el vector OB será el vector suma A A O B C B

Propiedades de la suma de vectores GEOGEBRA La suma de vectores tiene las siguientes propiedades § La suma de dos vectores libres es operación interna: § Es asociativa: § Existe elemento neutro: Es el vector nulo. Su representación es cualquier punto del plano § Existe elemento opuesto: El vector opuesto de u tiene la misma dirección y módulo que u pero sentido contrario § Es conmutativa:

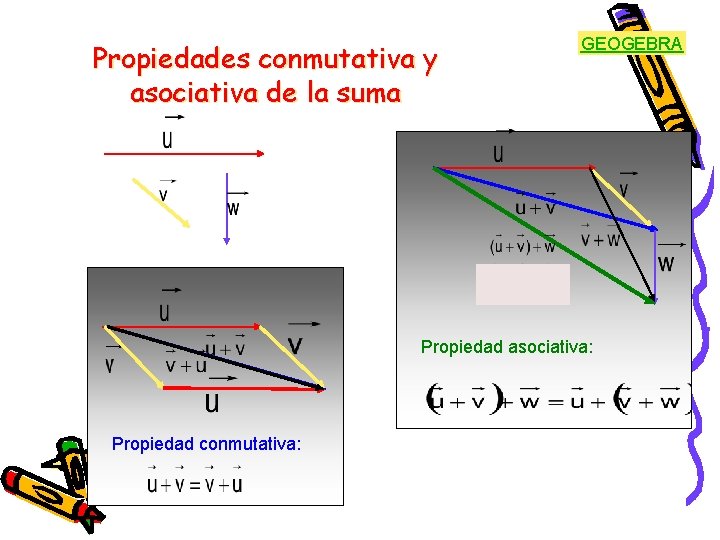
Propiedades conmutativa y asociativa de la suma GEOGEBRA Propiedad asociativa: Propiedad conmutativa:

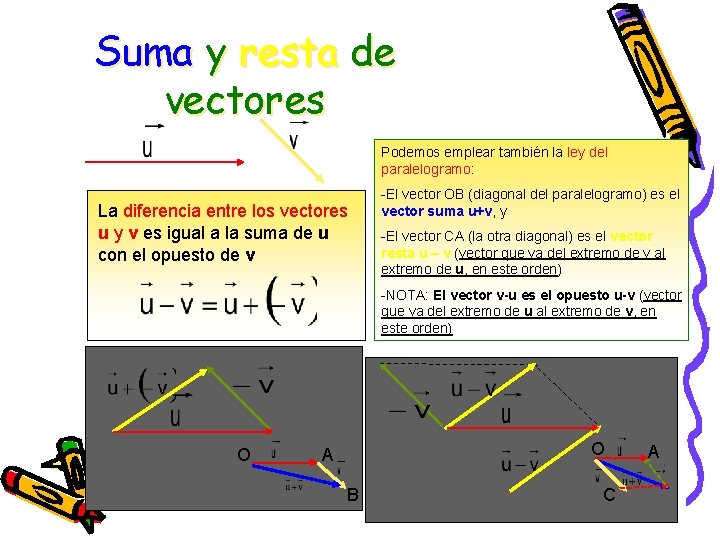
Suma y resta de vectores Podemos emplear también la ley del paralelogramo: La diferencia entre los vectores u y v es igual a la suma de u con el opuesto de v -El vector OB (diagonal del paralelogramo) es el vector suma u+v, y -El vector CA (la otra diagonal) es el vector resta u – v (vector que va del extremo de v al extremo de u, en este orden) -NOTA: El vector v-u es el opuesto u-v (vector que va del extremo de u al extremo de v, en este orden) O O A B C A

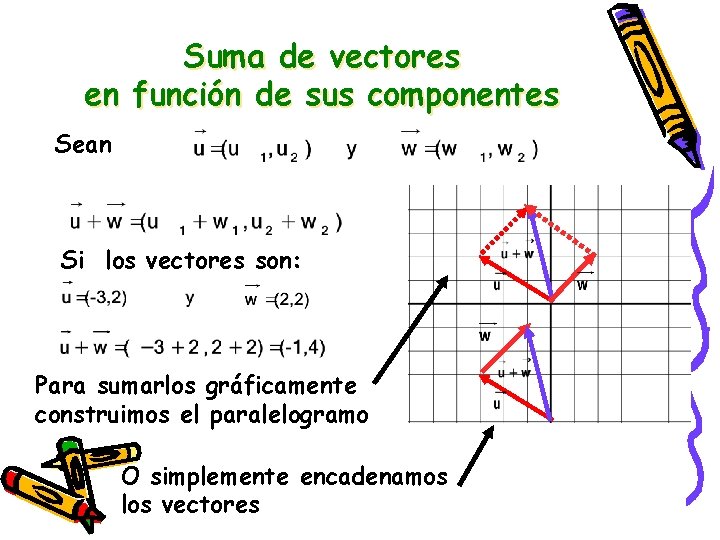
Suma de vectores en función de sus componentes Sean Si los vectores son: Para sumarlos gráficamente construimos el paralelogramo O simplemente encadenamos los vectores

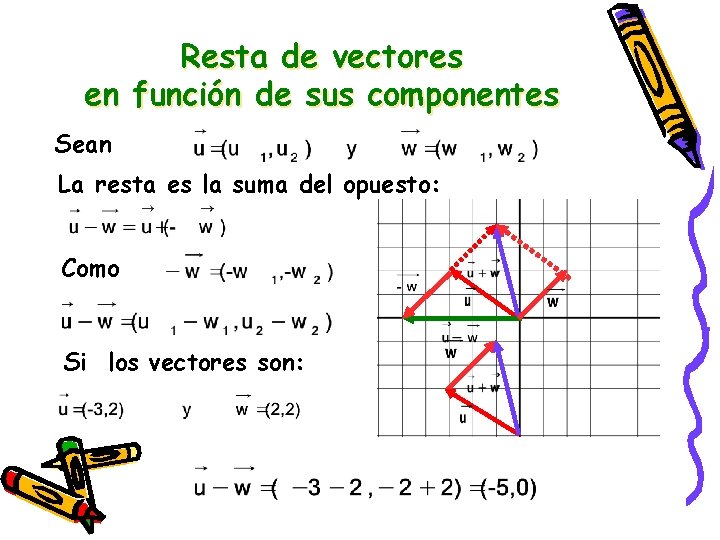
Resta de vectores en función de sus componentes Sean La resta es la suma del opuesto: Como Si los vectores son:

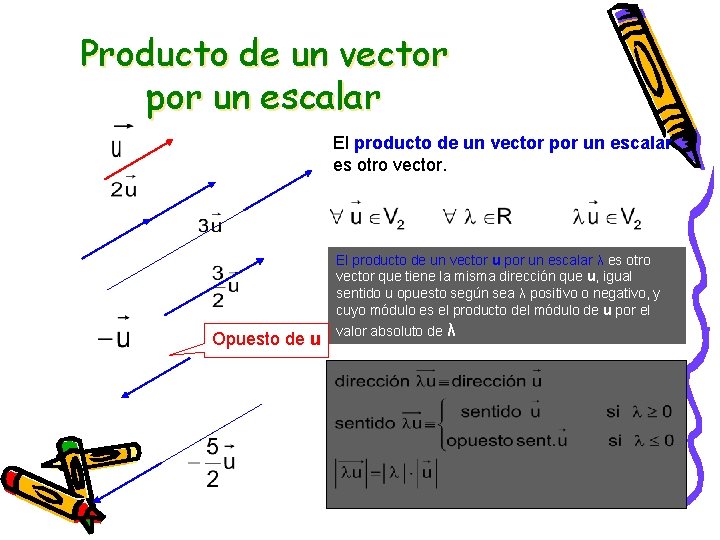
Producto de un vector por un escalar El producto de un vector por un escalar es otro vector. Opuesto de u El producto de un vector u por un escalar λ es otro vector que tiene la misma dirección que u, igual sentido u opuesto según sea λ positivo o negativo, y cuyo módulo es el producto del módulo de u por el valor absoluto de λ

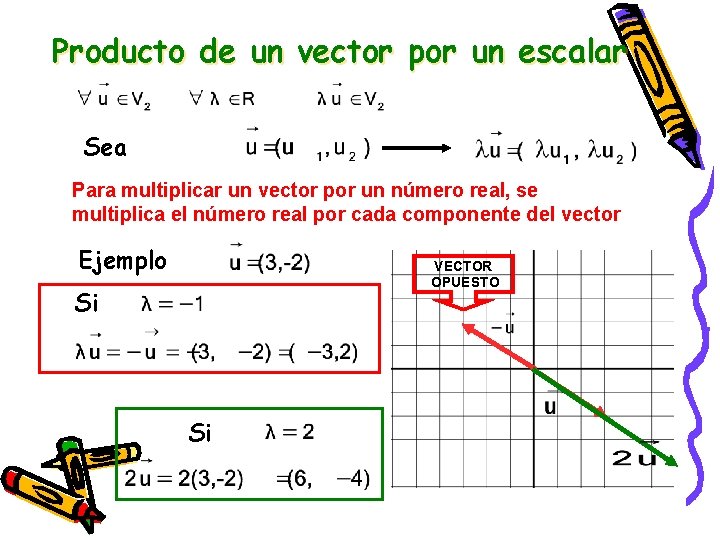
Producto de un vector por un escalar Sea Para multiplicar un vector por un número real, se multiplica el número real por cada componente del vector Ejemplo VECTOR OPUESTO Si Si

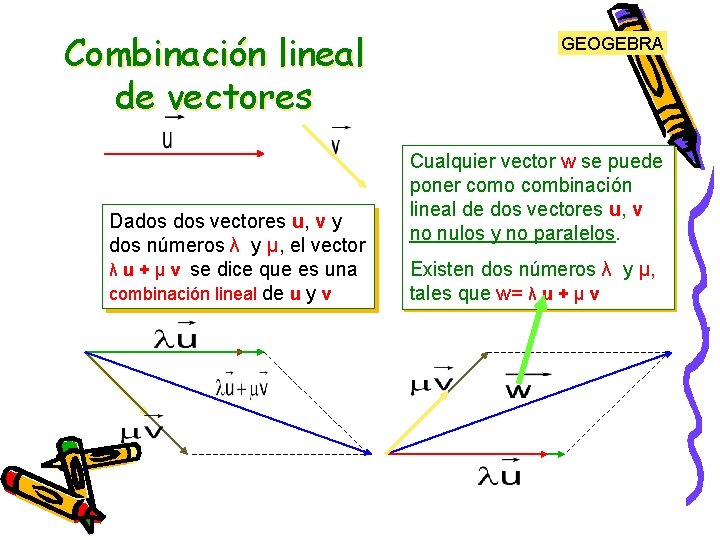
Combinación lineal de vectores Dados vectores u, v y dos números λ y µ, el vector λ u + µ v se dice que es una combinación lineal de u y v GEOGEBRA Cualquier vector w se puede poner como combinación lineal de dos vectores u, v no nulos y no paralelos. Existen dos números λ y µ, tales que w= λ u + µ v

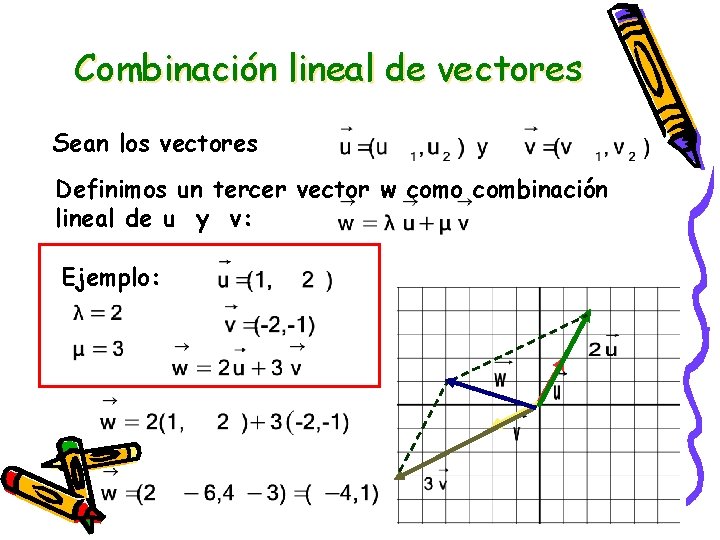
Combinación lineal de vectores Sean los vectores Definimos un tercer vector w como combinación lineal de u y v: Ejemplo:

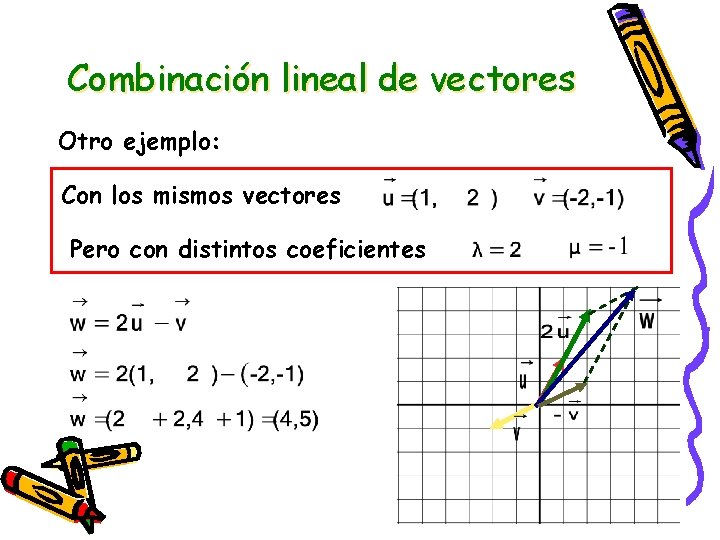
Combinación lineal de vectores Otro ejemplo: Con los mismos vectores Pero con distintos coeficientes

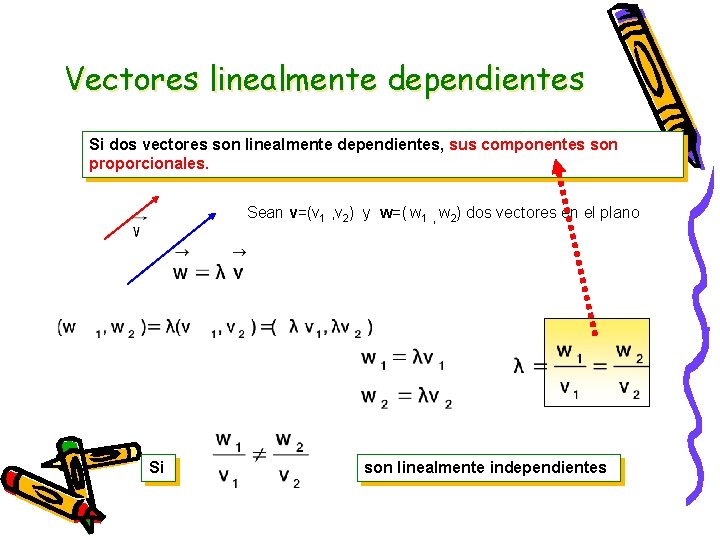
Vectores linealmente dependientes Si dos vectores son linealmente dependientes, sus componentes son proporcionales. Sean v=(v 1 , v 2) y w=( w 1 , w 2) dos vectores en el plano Si son linealmente independientes

Hoja de problemas con soluciones: http: //www. educa. aragob. es/iesitaza/DAPARTAM/matemat/06 ge ometriaplano. pdf Teoría y ejercicios: http: //personales. unican. es/gonzaleof/# Maneja vectores: http: //www. xtec. es/~jbartrol/vectores/index. html http: //platea. pntic. mec. es/anunezca/Unid. Did. Vectores/Index/index. htm