Variational Approaches and Image Segmentation Lecture 5 Hossam

Variational Approaches and Image Segmentation Lecture #5 Hossam Abdelmunim 1 & Aly A. Farag 2 1 Computer & Systems Engineering Department, Ain Shams University, Cairo, Egypt 2 Electerical and Computer Engineering Department, University of Louisville, KY, USA ECE 643 – Fall 2010 1

Variational Formulation in Computer Vision and Image Analysis Image/Curve/Surface is required to evolve to minimize a certain energy function. The change of the Image/Curve/Surface is described by a partial differential equation (PDE). In image segmentation, the evolution continuous until the curve/surface hits the object (region) boundaries.

Advantages of Introducing the Variational Formulation to the Computer Vision Field Modeling images in continuous time domain which simplifies the formalism and makes it grid independent. Research on numerical analysis makes it possible to achieve high speed, accurate, and stable solutions of the derived PDE’s. Viscosity solutions provide a framework for dealing with nonsmooth signals used with these approaches. Formal analysis in this area give the possibility of providing successful algorithms and useful theoretical results like existence and uniqueness of the solution.

Euler Lagrange & Gradient Descent (Recall) Given a real function: Define the following energy functional: The Euler Lagrange equation will be: The Gradient Descent will be:

Classical Deformable Models

Parametric Planar Curve Representation C(0. 5) Parametric Form: C(0) C(1) Arc Length is:

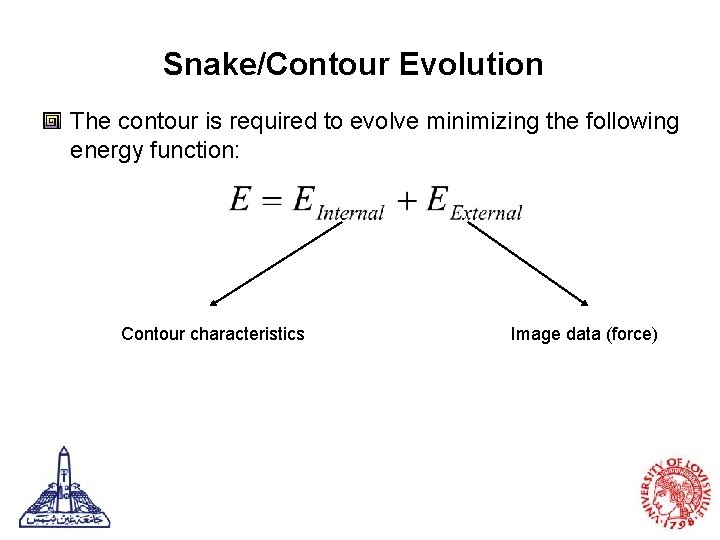
Snake/Contour Evolution The contour is required to evolve minimizing the following energy function: Contour characteristics Image data (force)

Internal Energy w 1 and w 2 are non negative. The term weighted by w 1 reduces curve length and removes ripples. The second term controls the bending and smoothness of the contour.

External Energy G is a Gaussian smoothing filter with width. λ is the magnitude of the external force. This term derives the contour towards the object boundaries.

Vector Valued PDE Using calculus of variation, the contour evolves according to the following equation:

Parametric Surfaces Representation and Evolution Parametric Form: Energy: v Complete the derivation. u

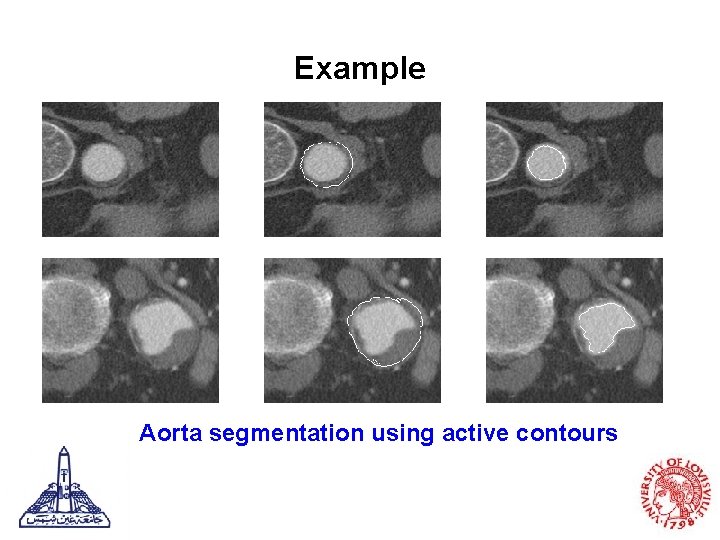
Example Aorta segmentation using active contours

Problems of Classical Deformable Models Dependency on the parameterization. Troubles with topology changes (merging/splitting). Initialization needs to be near the final solution (a big problem in 3 D). Tuning of the weighting coefficients in the PDE (w’s, λ).

Level Sets

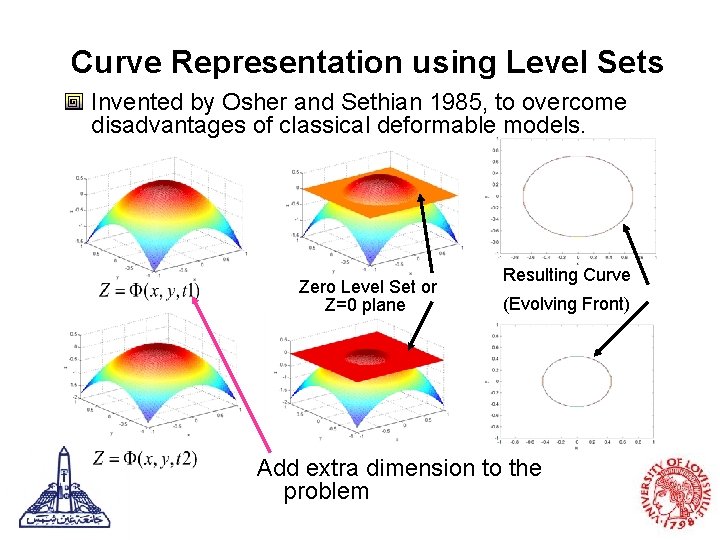
Curve Representation using Level Sets Invented by Osher and Sethian 1985, to overcome disadvantages of classical deformable models. Zero Level Set or Z=0 plane Resulting Curve (Evolving Front) Add extra dimension to the problem

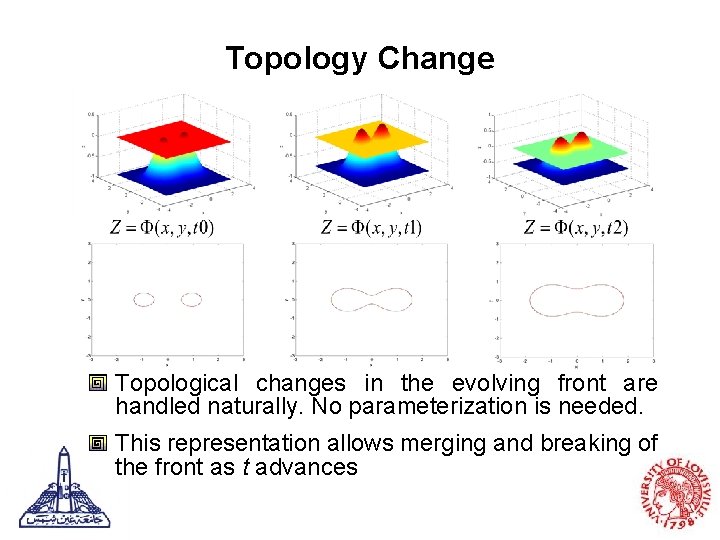
Topology Change Topological changes in the evolving front are handled naturally. No parameterization is needed. This representation allows merging and breaking of the front as t advances

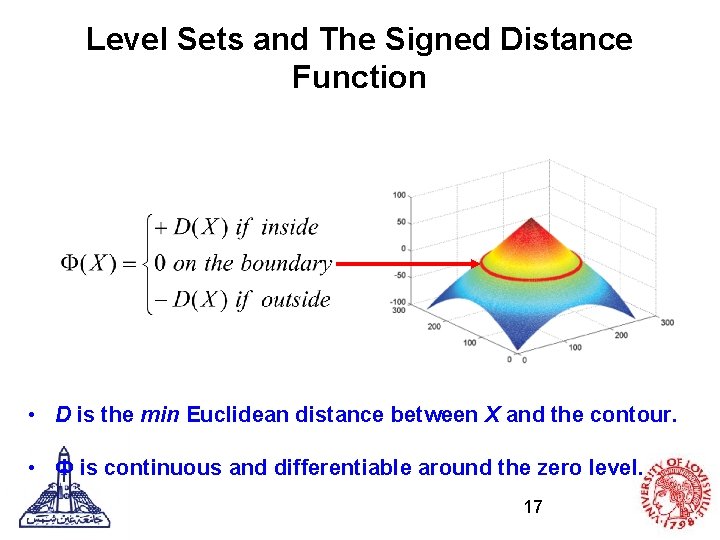
Level Sets and The Signed Distance Function • D is the min Euclidean distance between X and the contour. • Ф is continuous and differentiable around the zero level. 17

Example of Signed Distance Functions w. N

Example of Image Representation

Applications of the Distance Transform (DT) The DT is a fundamental operator in shape analysis, having numerous applications, some of which are briefly listed bellow. • Separation of overlapping objects through watershed segmentation. • Computation of morphological operators. • Computation of geometrical representations and measures, such as skeletonization. • Shape matching. • Shape measures related to distance. • Other interesting areas in which the DT has been applied are: • image registration • subpixel contour tracing • multidimensional data analysis (classification, clustering) • image enhancement • ray-tracing optimization • embedding surface for level set-based methods • efficient belief-propagation • multiphase flow simulations • medical image analysis • analysis of interaction between biological structures

Signed Distance Generation Complexity So, to compute the distance function you need to get the closest point on the boundary/curve for each position in the domain. This process is very time-consuming especially for volumes in 3 D and higher. Some approximation methods are used to expedite this process. See the following slides.

Distance Transform Generation Faster Algorithm 1. 2. 3. Set boundary points to zeroes while others to ∞. Initialize an auxiliary set of pixels (usually a queue), the so-called contour set, with the boundary pixels and their zero values. While the contour set is not empty do the following: a) Remove a pixel from the contour set. Let us call it the central pixel (xp, yp) now. b) For every pixel (xq, yq) of the neighbors of the central pixel, do the following: I. Compute the distance to the central point as: dd=|xp-xq|+|yp-yq|; II. Compute a temporary distance as : dtq=min(dist(p)+dd, dist(q)); III. If dtq < dist(q), add the pixel q to the contour set; IV. Dist(q)=dtq; ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ 0 0 0 ∞ ∞ ∞ ∞ ∞ 0 ∞ ∞ ∞ 0 ∞ ∞ ∞ ∞ ∞ 0 0 0 ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞

Distance Transform Generation Faster Algorithm (Cont…) • Note that computing the distance as the difference is faster than the square root function. • Also, this methodology updates the distance values around the boundary points/pixels until there are no points in the queue. • Try this method with the dynamic implementation using linked lists. It will be much faster than the ordinary methods…. Assignment: Implement using C++. Apply it for 2 D as well as 3 D shapes.