Variability Variability n Variability q n How tightly

Variability

Variability n Variability q n How tightly clustered or how widely dispersed the values are in a data set. Example q q q Data set 1: [0, 25, 50, 75, 100] Data set 2: [48, 49, 50, 51, 52] Both have a mean of 50, but data set 1 clearly has greater Variability than data set 2.

Variability: The Range n The Range is one measure of variability q n The range is the difference between the maximum and minimum values in a set Example q q Data set 1: [1, 25, 50, 75, 100]; R: 100 -0 +1 = 100 Data set 2: [48, 49, 50, 51, 52]; R: 52 -48 + 1= 5 The range ignores how data are distributed and only takes the extreme scores into account RANGE = (Xlargest – Xsmallest) + 1

Quartiles n Split Ordered Data into 4 Quarters 25% 25% n = first quartile n = second quartile= Median n = third quartile 25%

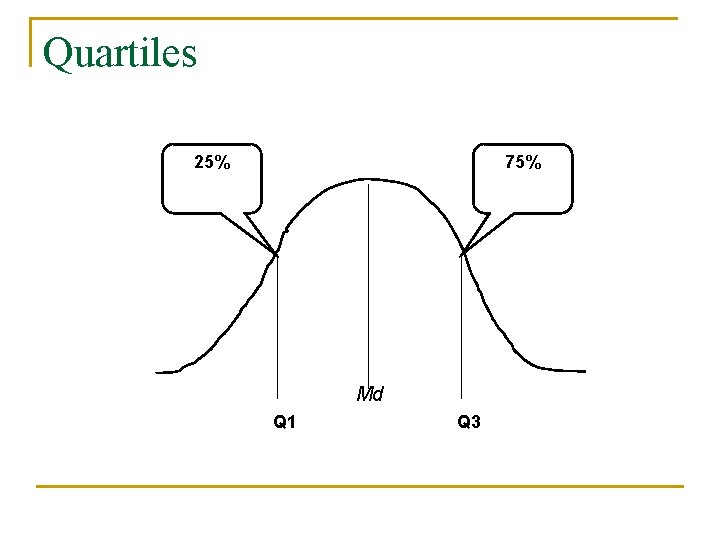
Quartiles 25% 75% Md Q 1 Q 3

Variability: Interquartile Range n Difference between third & first quartiles q Interquartile Range = Q 3 - Q 1 n Spread in middle 50% n Not affected by extreme values

Standard Deviation and Variance n How much do scores deviate from the mean? q deviation = X X- 1 0 6 1 =2 n Why not just add these all up and take the mean?

Standard Deviation and Variance n Solve the problem by squaring the deviations! X- (X- )2 1 -1 1 0 -2 4 6 +4 16 1 -1 1 X =2 Variance =

Standard Deviation and Variance n n n Higher value means greater variability around Critical for inferential statistics! But, not as useful as a purely descriptive statistic q n hard to interpret “squared” scores! Solution un-square the variance! Standard Deviation =

Variability: Standard Deviation n n n The Standard Deviation tells us approximately how far the scores vary from the mean on average estimate of average deviation/distance from small value means scores clustered close to large value means scores spread farther from Overall, most common and important measure extremely useful as a descriptive statistic extremely useful in inferential statistics The typical deviation in a given distribution

Variability: Standard Deviation n Standard Deviation can be calculated with the sum of squares (SS) divided by n

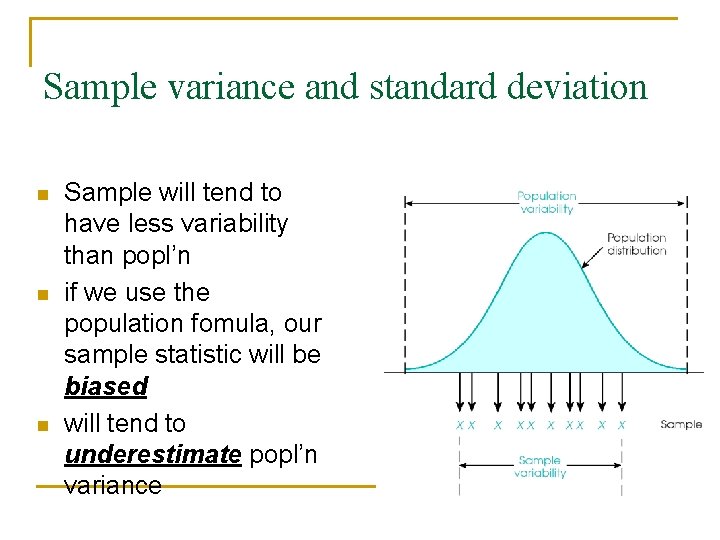
Sample variance and standard deviation n Sample will tend to have less variability than popl’n if we use the population fomula, our sample statistic will be biased will tend to underestimate popl’n variance

Sample variance and standard deviation n n n Correct for problem by adjusting formula Different symbol: s 2 vs. 2 Different denominator: n-1 vs. N n-1 = “degrees of freedom” Everything else is the same Interpretation is the same

Definitional Formula: Variance: deviation Standard n squared-deviation Deviation: n ‘Sum of Squares’ = SS n degrees of freedom n

Variability: Standard Deviation q q q let X = [3, 4, 5 , 6, 7] M=5 (X - M) = [-2, -1, 0, 1, 2] ñ subtract M from each number in X q (X - M)2 = [4, 1, 0, 1, 4] ñ squared deviations from the mean q S (X - M)2 = 10 ñ sum of squared deviations from the mean (SS) q S (X - M)2 /n-1 = 10/5 = 2. 5 ñ average squared deviation from the mean q S (X - M)2 /n-1 = 2. 5 = 1. 58 ñ square root of averaged squared deviation

Variability: Standard Deviation q q q let X = [1, 3, 5, 7, 9] M=5 (X - M) = [-4, -2, 0, 2, 4 ] ñ subtract M from each number in X q (X - M)2 = [16, 4, 0, 4, 16] ñ squared deviations from the mean q S (X - M)2 = 40 ñ sum of squared deviations from the mean (SS) q S (X - M)2 /n-1 = 40/4 = 10 ñ average squared deviation from the mean q S (X - M)2 /n-1 = 10 = 3. 16 ñ square root of averaged squared deviation

In class example n Work on handout

Standard Deviation & Standard Scores n Z scores are expressed in the following way n Z scores express how far a particular score is from the mean in units of standard deviation

Standard Deviation & Standard Scores n Z scores provide a common scale to express deviations from a group mean

Standard Deviation and Standard Scores n Let’s say someone has an IQ of 145 and is 52 inches tall q q n n IQ in a population has a mean of 100 and a standard deviation of 15 Height in a population has a mean of 64” with a standard deviation of 4 How many standard deviations is this person away from the average IQ? How many standard deviations is this person away from the average height?

Homework n Chapter 4 q 8, 9, 11, 12, 16, 17