Use of moment generating functions Definition Let X








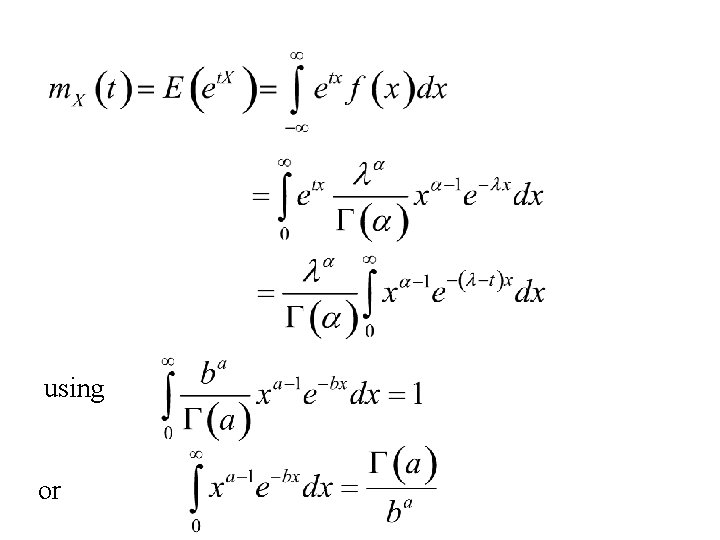
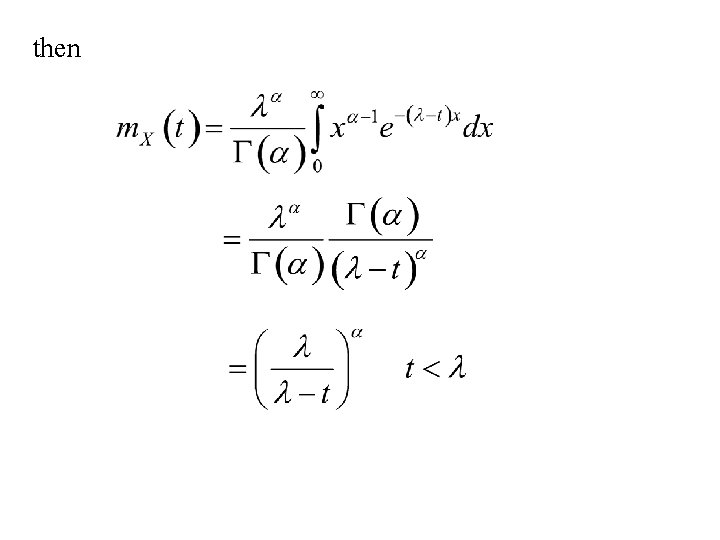

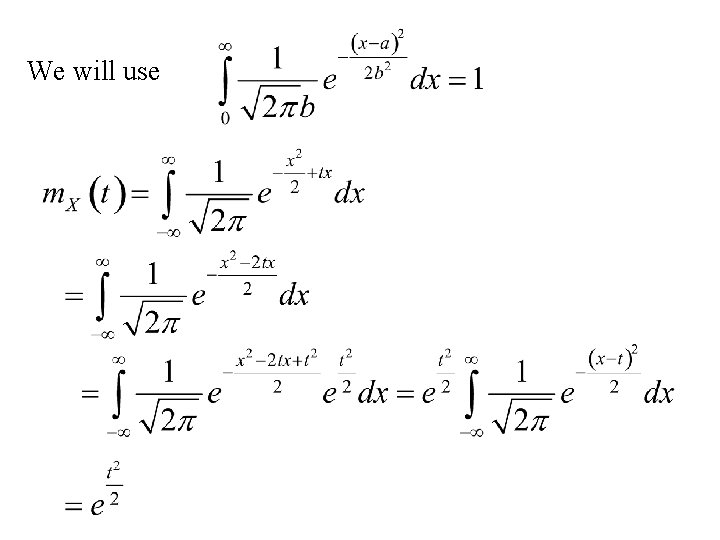
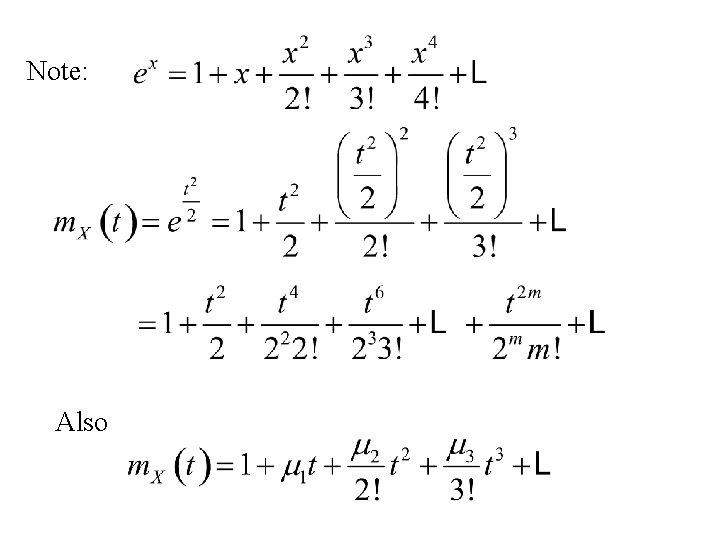
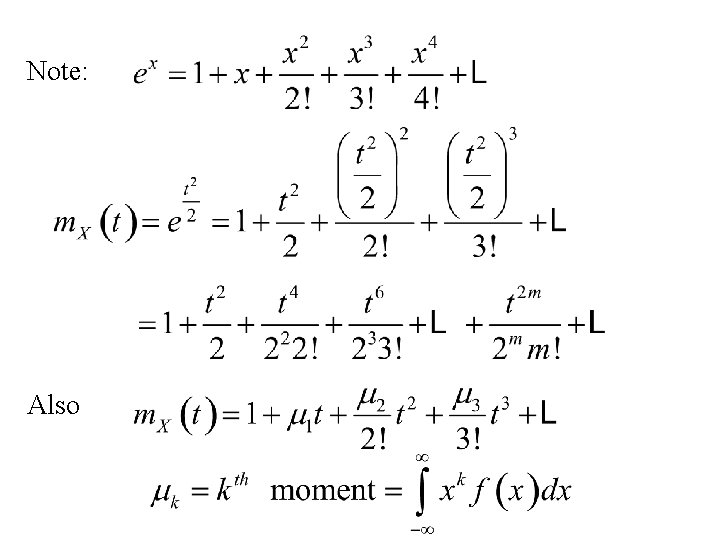
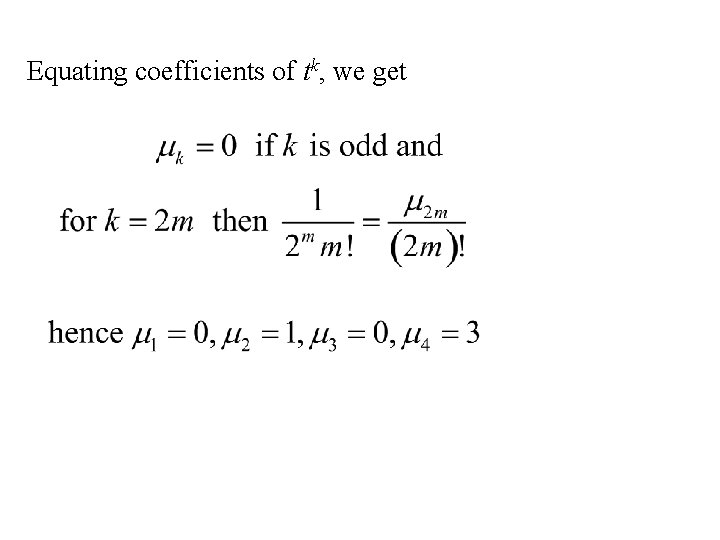





















- Slides: 38

Use of moment generating functions

Definition Let X denote a random variable with probability density function f(x) if continuous (probability mass function p(x) if discrete) Then m. X(t) = the moment generating function of X

The distribution of a random variable X is described by either 1. The density function f(x) if X continuous (probability mass function p(x) if X discrete), or 2. The cumulative distribution function F(x), or 3. The moment generating function m. X(t)

Properties 1. m. X(0) = 1 2. 3.

4. Let X be a random variable with moment generating function m. X(t). Let Y = b. X + a Then m. Y(t) = mb. X + a(t) = E(e [b. X + a]t) = eatm. X (bt) 5. Let X and Y be two independent random variables with moment generating function m. X(t) and m. Y(t). Then m. X+Y(t) = m. X (t) m. Y (t)

6. Let X and Y be two random variables with moment generating function m. X(t) and m. Y(t) and two distribution functions FX(x) and FY(y) respectively. Let m. X (t) = m. Y (t) then FX(x) = FY(x). This ensures that the distribution of a random variable can be identified by its moment generating function

M. G. F. ’s - Continuous distributions

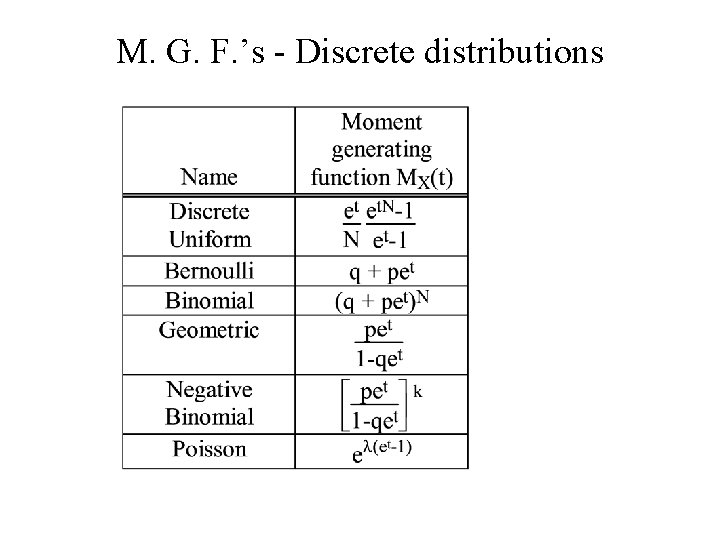
M. G. F. ’s - Discrete distributions

Moment generating function of the gamma distribution where
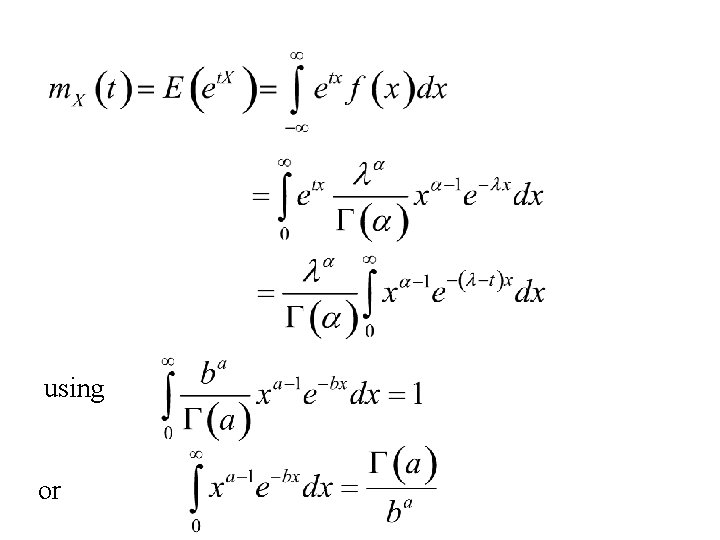
using or
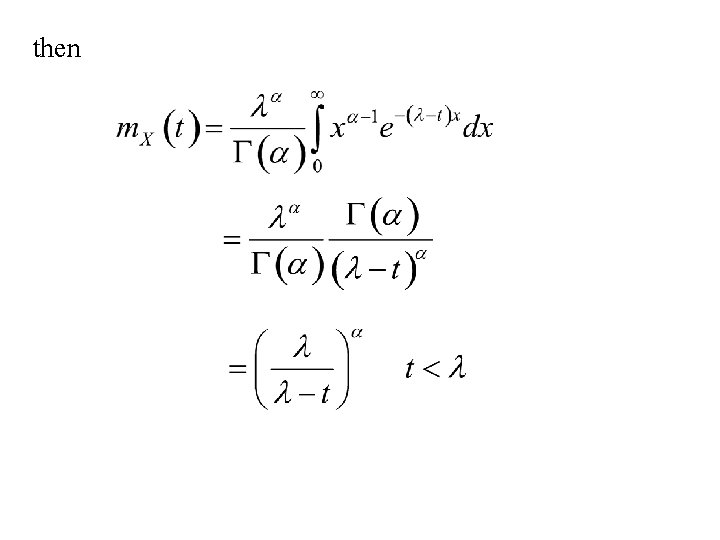
then

Moment generating function of the Standard Normal distribution where thus
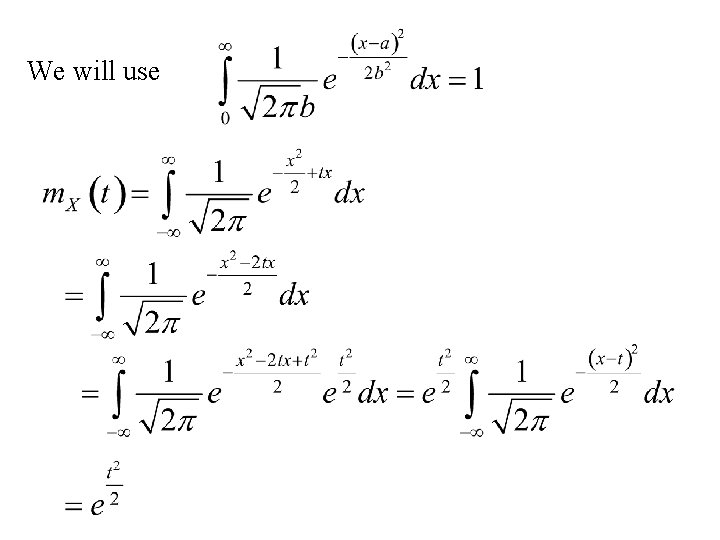
We will use
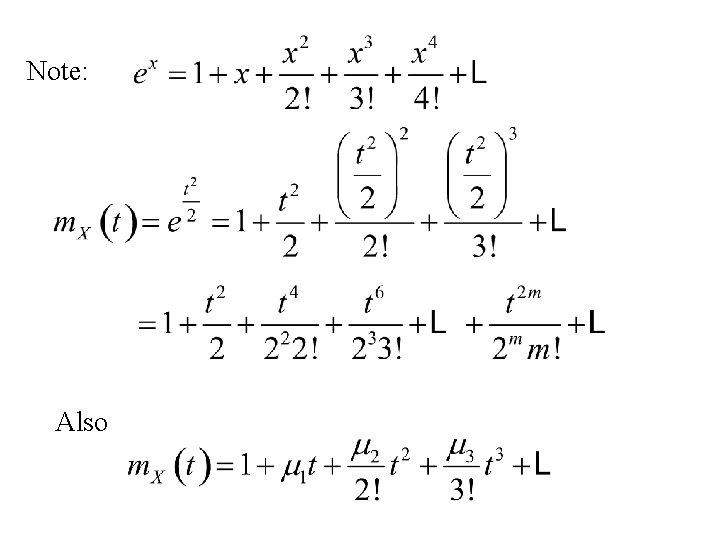
Note: Also
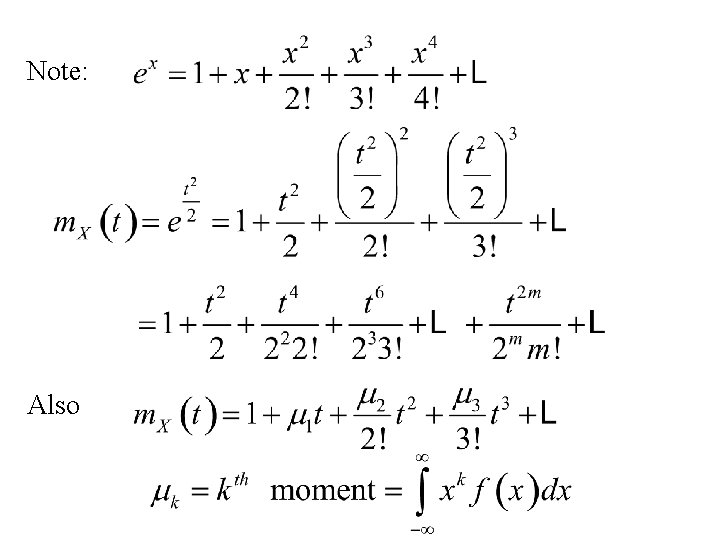
Note: Also
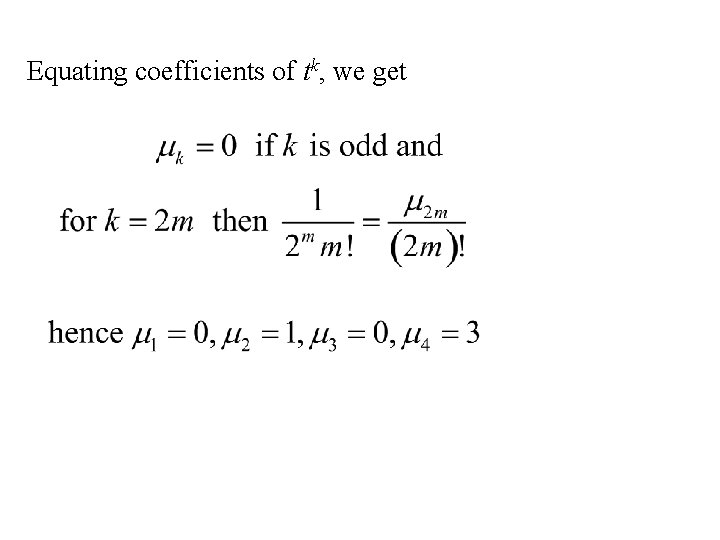
Equating coefficients of tk, we get

Using of moment generating functions to find the distribution of functions of Random Variables

Example Suppose that X has a normal distribution with mean m and standard deviation s. Find the distribution of Y = a. X + b Solution: = the moment generating function of the normal distribution with mean am + b and variance a 2 s 2.

Thus Y = a. X + b has a normal distribution with mean am + b and variance a 2 s 2. Special Case: the z transformation Thus Z has a standard normal distribution.

Example Suppose that X and Y are independent each having a normal distribution with means m. X and m. Y , standard deviations s. X and s. Y Find the distribution of S = X + Y Solution: Now

or = the moment generating function of the normal distribution with mean m. X + m. Y and variance Thus Y = X + Y has a normal distribution with mean m. X + m. Y and variance

Example Suppose that X and Y are independent each having a normal distribution with means m. X and m. Y , standard deviations s. X and s. Y Find the distribution of L = a. X + b. Y Solution: Now

or = the moment generating function of the normal distribution with mean am. X + bm. Y and variance Thus Y = a. X + b. Y has a normal distribution with mean am. X + Bm. Y and variance

Special Case: a = +1 and b = -1. Thus Y = X - Y has a normal distribution with mean m. X - m. Y and variance

Example (Extension to n independent RV’s) Suppose that X 1, X 2, …, Xn are independent each having a normal distribution with means mi, standard deviations si (for i = 1, 2, … , n) Find the distribution of L = a 1 X 1 + a 1 X 2 + …+ an. Xn Solution: (for i = 1, 2, … , n) Now

or = the moment generating function of the normal distribution with mean and variance Thus Y = a 1 X 1 + … + an. Xn has a normal distribution with mean a 1 m 1 + …+ anmn and variance

Special case: In this case X 1, X 2, …, Xn is a sample from a normal distribution with mean m, and standard deviations s, and

Thus has a normal distribution with mean and variance

Summary If x 1, x 2, …, xn is a sample from a normal distribution with mean m, and standard deviations s, then has a normal distribution with mean and variance

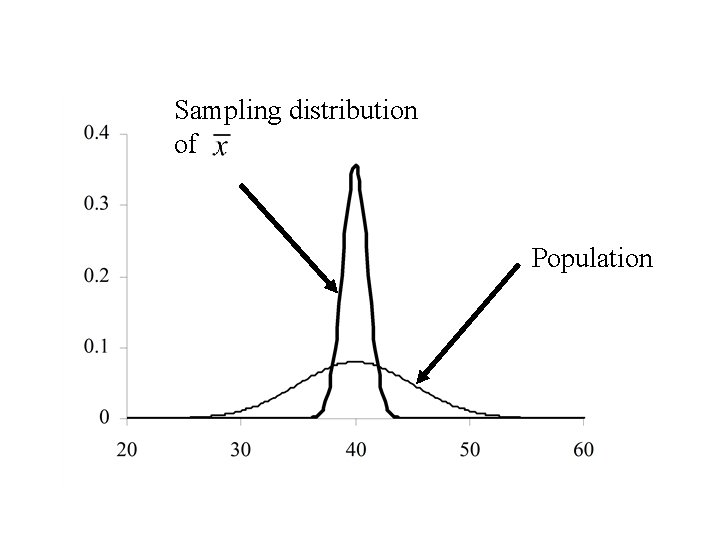
Sampling distribution of Population

The Central Limit theorem If x 1, x 2, …, xn is a sample from a distribution with mean m, and standard deviations s, then if n is large has a normal distribution with mean and variance

Proof: (use moment generating functions) We will use the following fact: Let m 1(t), m 2(t), … denote a sequence of moment generating functions corresponding to the sequence of distribution functions: F 1(x) , F 2(x), … Let m(t) be a moment generating function corresponding to the distribution function F(x) then if then

Let x 1, x 2, … denote a sequence of independent random variables coming from a distribution with moment generating function m(t) and distribution function F(x). Let Sn = x 1 + x 2 + … + xn then





Is the moment generating function of the standard normal distribution Thus the limiting distribution of z is the standard normal distribution Q. E. D.
 Let me let me let me
Let me let me let me Uses of moment generating function
Uses of moment generating function Moment generating function of bernoulli distribution
Moment generating function of bernoulli distribution Multinomial distribution mgf
Multinomial distribution mgf Moment generating function of normal distribution
Moment generating function of normal distribution Uniform distribution formula
Uniform distribution formula Gamma function properties
Gamma function properties Generating functions
Generating functions Let's let them object to another one
Let's let them object to another one Go to my house
Go to my house He who has ears to hear and eyes to see
He who has ears to hear and eyes to see Standard generating body
Standard generating body Tourist generating region adalah
Tourist generating region adalah Innovative ideas for revenue generation
Innovative ideas for revenue generation Generating sentences from a continuous space
Generating sentences from a continuous space A generating voltmeter uses
A generating voltmeter uses Discuss midpoint ellipse drawing algorithms.
Discuss midpoint ellipse drawing algorithms. Define new entry in entrepreneurship
Define new entry in entrepreneurship Recognizing opportunities and generating ideas
Recognizing opportunities and generating ideas Acebf
Acebf Generating alpha meaning
Generating alpha meaning Generating hard instances of lattice problems
Generating hard instances of lattice problems Contoh soal fungsi pembangkit momen
Contoh soal fungsi pembangkit momen Exe: automatically generating inputs of death
Exe: automatically generating inputs of death Exe: automatically generating inputs of death
Exe: automatically generating inputs of death Are the different types of generating control signals
Are the different types of generating control signals An opportunity has four essential qualities it is
An opportunity has four essential qualities it is Recognising opportunities
Recognising opportunities Robert marzano high yield strategies
Robert marzano high yield strategies Autocovariance generating function
Autocovariance generating function Porter service
Porter service Difference between shaper and planer
Difference between shaper and planer Currents unit
Currents unit Gst notification on solar power generating system
Gst notification on solar power generating system Generating alternative solutions
Generating alternative solutions Recognizing opportunities and generating ideas
Recognizing opportunities and generating ideas Absolute value as a piecewise function
Absolute value as a piecewise function Evaluating functions and operations on functions
Evaluating functions and operations on functions Evaluating functions and operations on functions
Evaluating functions and operations on functions


























































