Troisime et Quatrime cours de physique Etat quantique

Troisième et Quatrième cours de physique

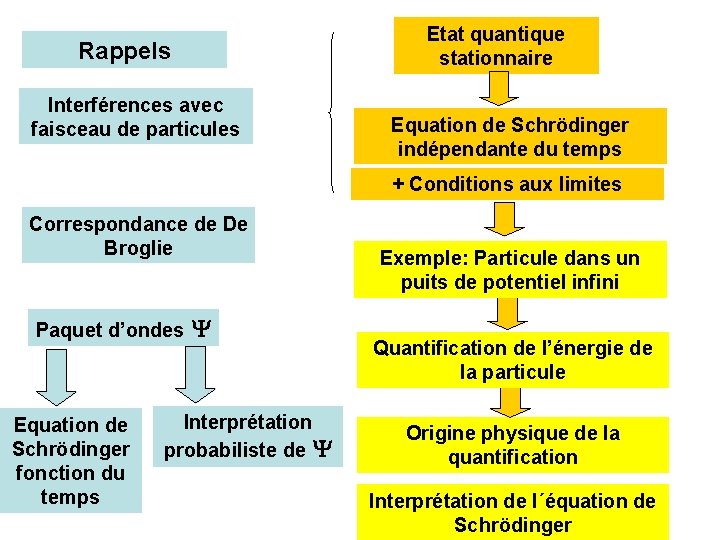
Etat quantique stationnaire Rappels Interférences avec faisceau de particules Equation de Schrödinger indépendante du temps + Conditions aux limites Correspondance de De Broglie Paquet d’ondes Equation de Schrödinger fonction du temps Interprétation probabiliste de Exemple: Particule dans un puits de potentiel infini Quantification de l’énergie de la particule Origine physique de la quantification Interprétation de l´équation de Schrödinger

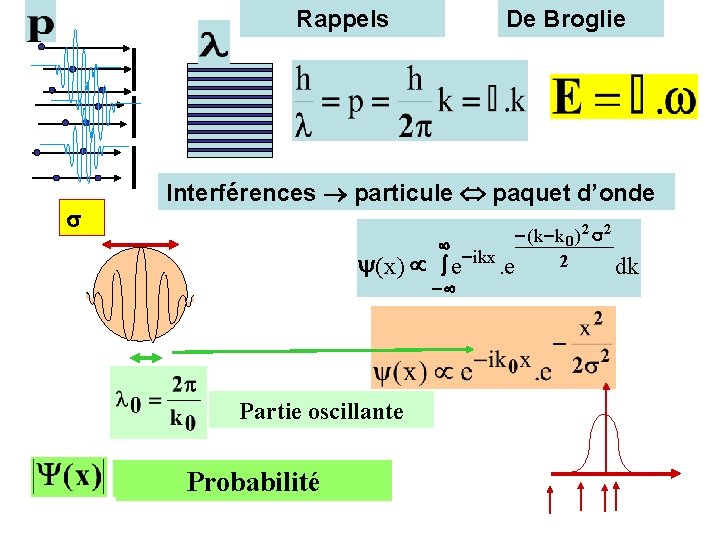
Rappels De Broglie Interférences particule paquet d’onde (x ) µ Partie oscillante Extension spatiale Probabilité - (k - k 0 )2 2 ¥ - ikx 2. e dk òe -¥

Interférences avec des particules (animation)

Interférences avec des particules (animation)

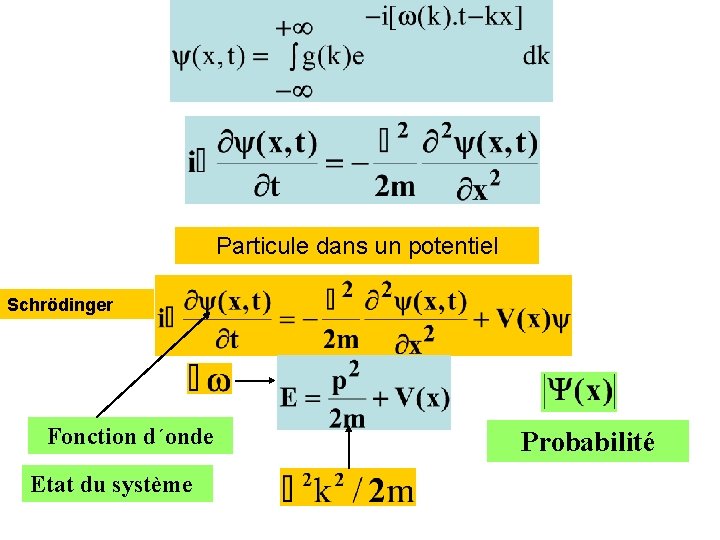
Particule dans un potentiel Schrödinger Fonction d´onde Etat du système Probabilité

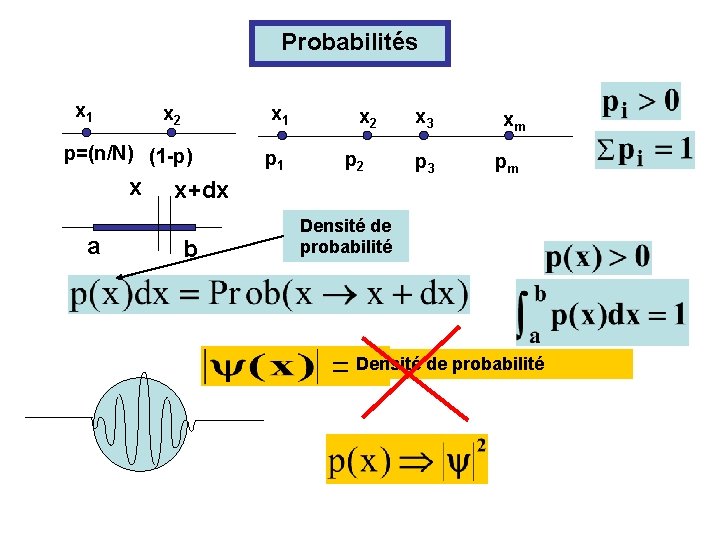
Probabilités x 1 x 2 x 1 p=(n/N) (1 -p) x a p 1 x 2 p 2 x+dx b x 3 p 3 xm pm Densité de probabilité

Etats stationnaires Equation de Schrödinger indépendante du temps

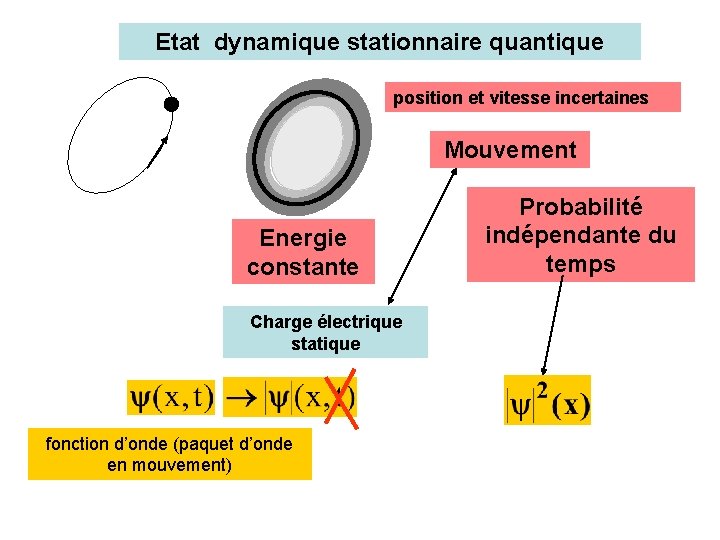
Etat dynamique stationnaire quantique position et vitesse incertaines Mouvement Energie constante Charge électrique statique fonction d’onde (paquet d’onde en mouvement) Probabilité indépendante du temps

Détermination des états stationnaires 1°) = amplitude de probabilité de présence de la particule 2°) = densité de probabilité de présence de la particule Fonction de carré sommable Norme=1 3°) Solution de l’équation de Schrödinger 4°) Conditions aux limites + 5°) Etats liés

Particule de masse m dans un « puits de potentiel infini » m

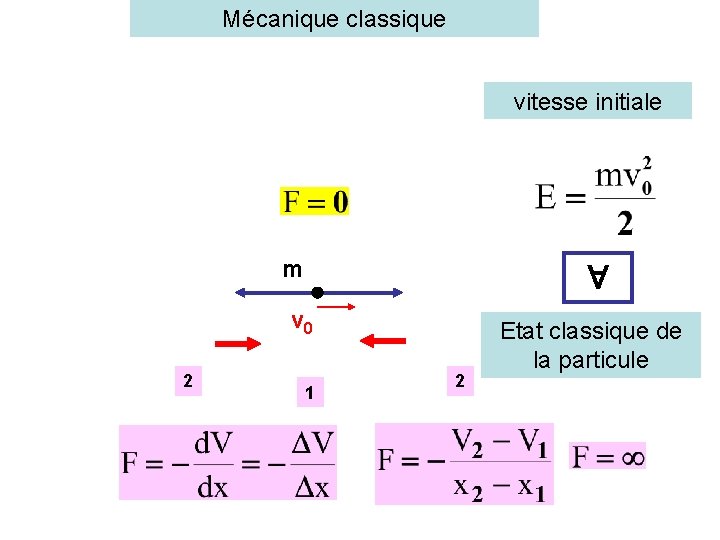
Mécanique classique vitesse initiale m v 0 2 1 2 Etat classique de la particule

Mécanique quantique m

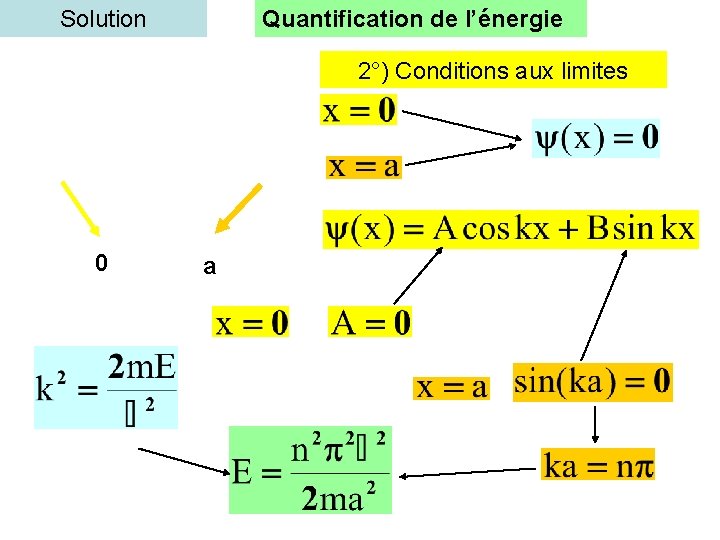
Solution 1°) Equation de Schrödinger des états stationnaires E>0

Solution Quantification de l’énergie 2°) Conditions aux limites 0 a

Solution 0 3°) Norme (Carré sommable) a n= 1, 2, 3, . . . Etats possibles de la particule n Nombre quantique

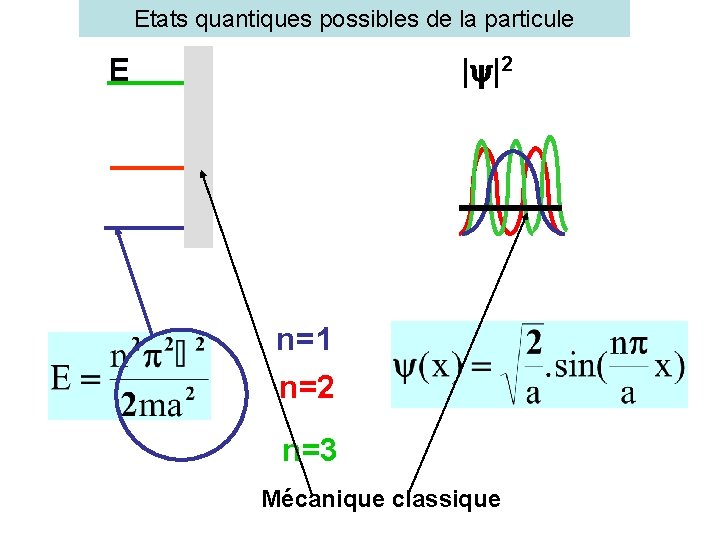
Etats quantiques possibles de la particule E | |2 n=1 n=2 n=3 Mécanique classique

Entracte 10 minutes

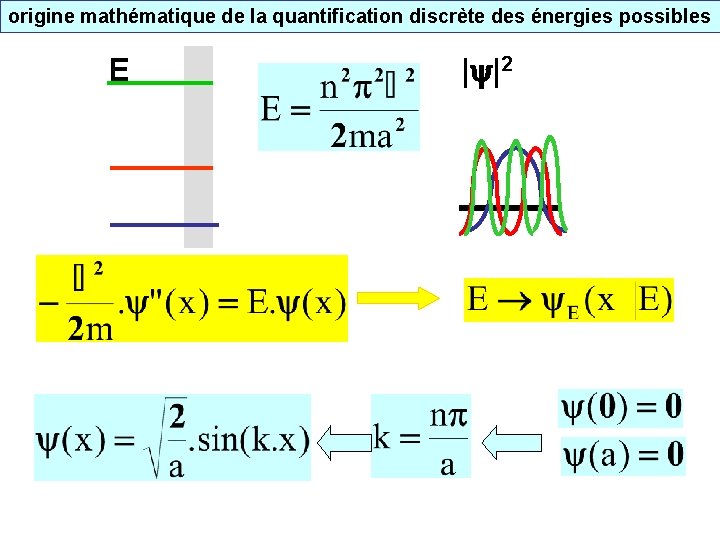
origine mathématique de la quantification discrète des énergies possibles E | |2

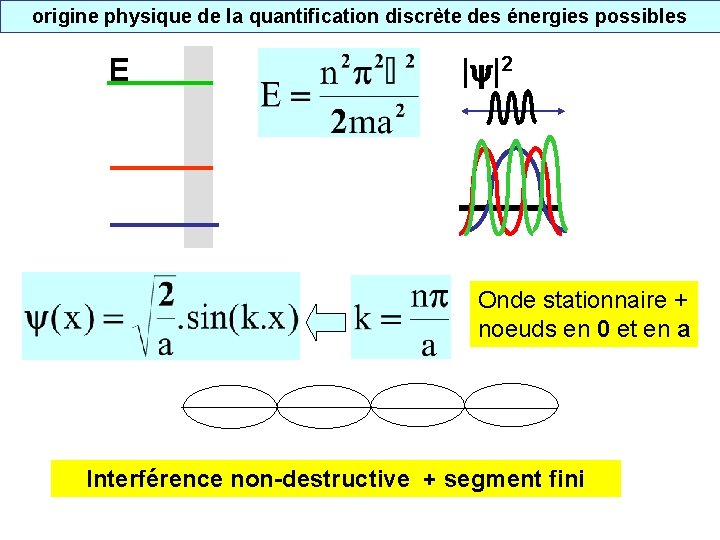
origine physique de la quantification discrète des énergies possibles E | |2 Onde stationnaire + noeuds en 0 et en a Interférence non-destructive + segment fini

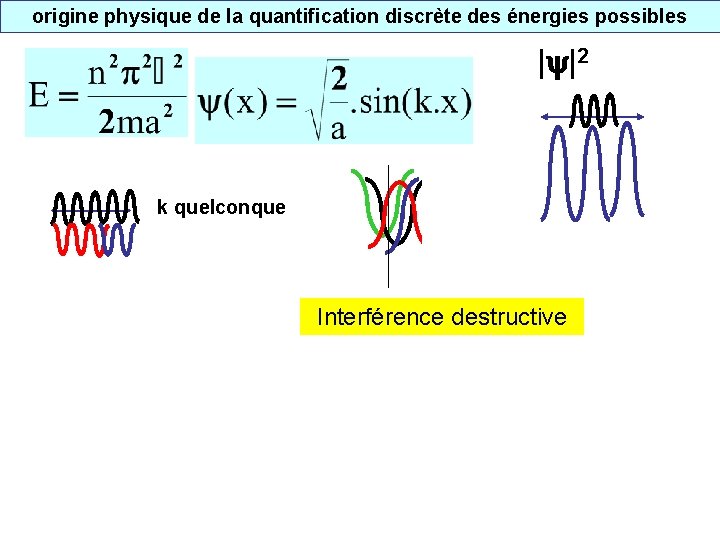
origine physique de la quantification discrète des énergies possibles | |2 k quelconque Interférence destructive

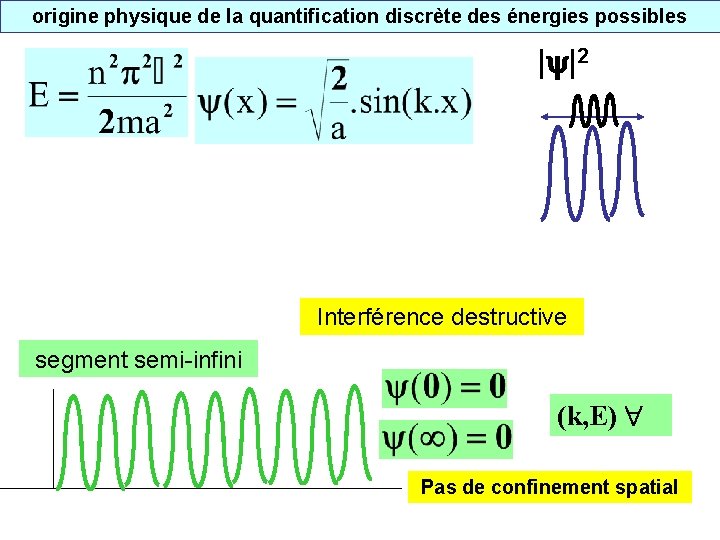
origine physique de la quantification discrète des énergies possibles | |2 Interférence destructive segment semi-infini (k, E) Pas de confinement spatial

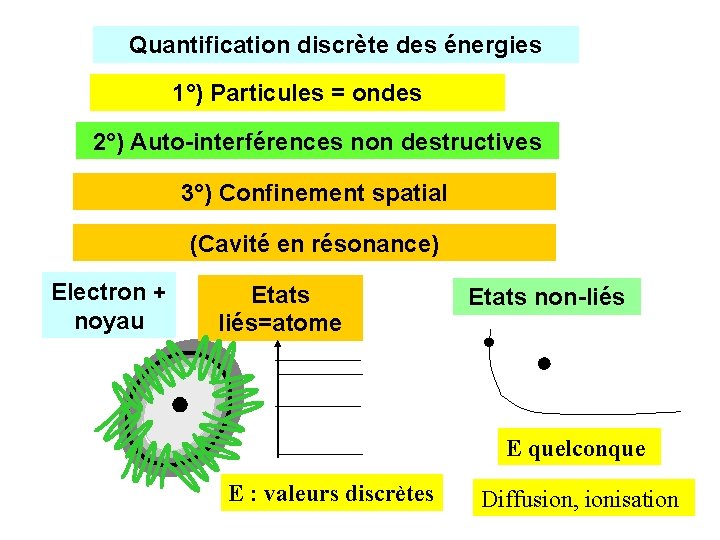
Quantification discrète des énergies 1°) Particules = ondes 2°) Auto-interférences non destructives 3°) Confinement spatial (Cavité en résonance) Electron + noyau Etats liés=atome Etats non-liés E quelconque E : valeurs discrètes Diffusion, ionisation

Signification de l’équation de Schrödinger Opérateur différentiel Opérateur multiplicatif opérateur linéaire

Signification de l’équation de Schrödinger Opérateur linéaire

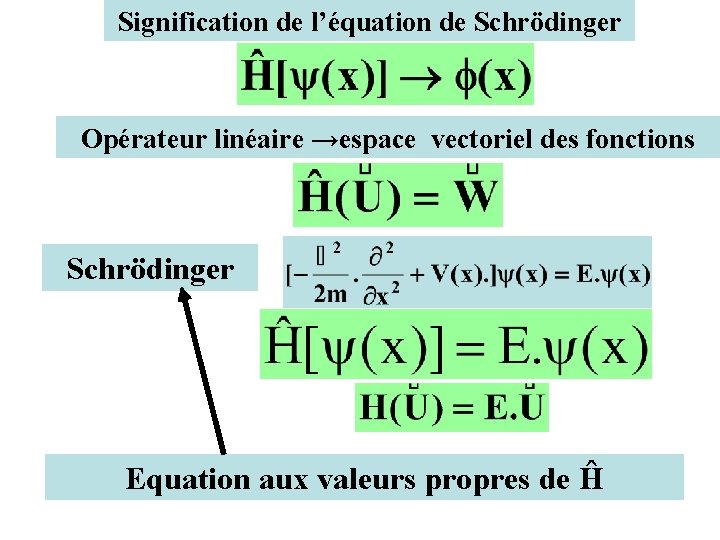
Signification de l’équation de Schrödinger Opérateur linéaire →espace vectoriel des fonctions Schrödinger Equation aux valeurs propres de Ĥ

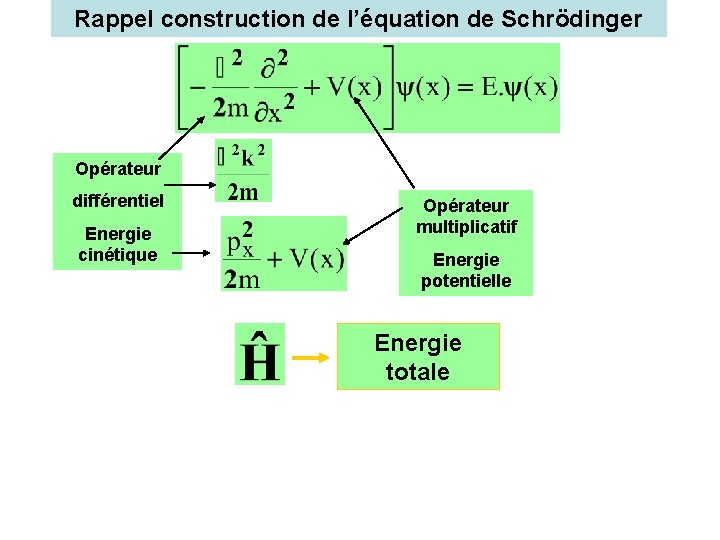
Rappel construction de l’équation de Schrödinger Opérateur différentiel Energie cinétique Opérateur multiplicatif Energie potentielle Energie totale

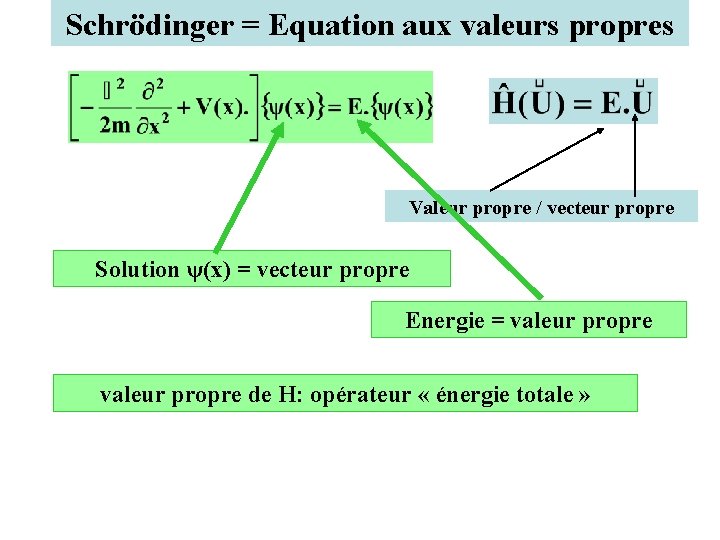
Schrödinger = Equation aux valeurs propres Valeur propre / vecteur propre Solution ψ(x) = vecteur propre Energie = valeur propre de H: opérateur « énergie totale »

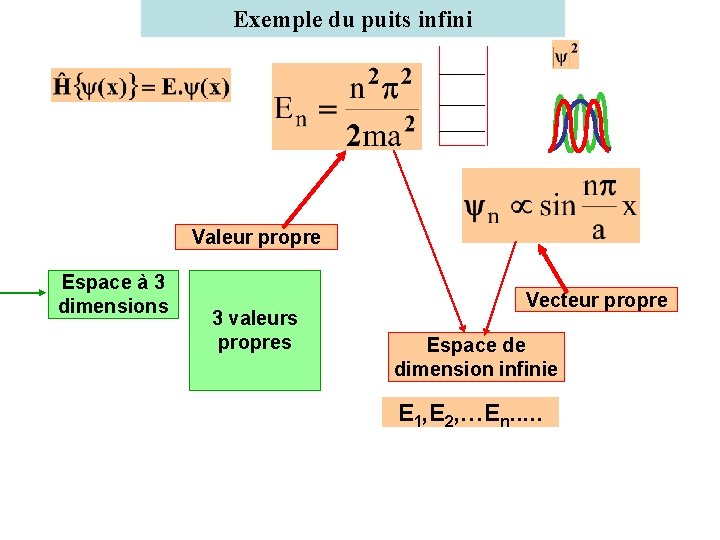
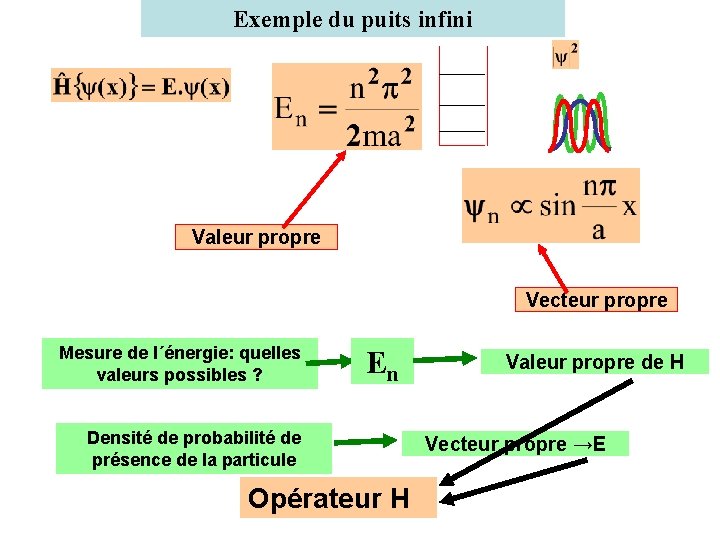
Exemple du puits infini Valeur propre Espace à 3 dimensions 3 valeurs propres Vecteur propre Espace de dimension infinie E 1, E 2, …En. . .

Exemple du puits infini Valeur propre Vecteur propre Mesure de l´énergie: quelles valeurs possibles ? En Densité de probabilité de présence de la particule Opérateur H Valeur propre de H Vecteur propre →E

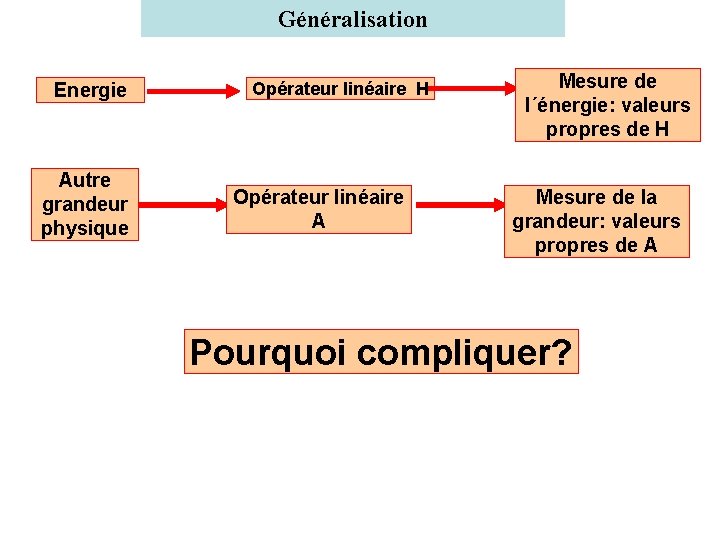
Généralisation Energie Autre grandeur physique Opérateur linéaire H Opérateur linéaire A Mesure de l´énergie: valeurs propres de H Mesure de la grandeur: valeurs propres de A Pourquoi compliquer?

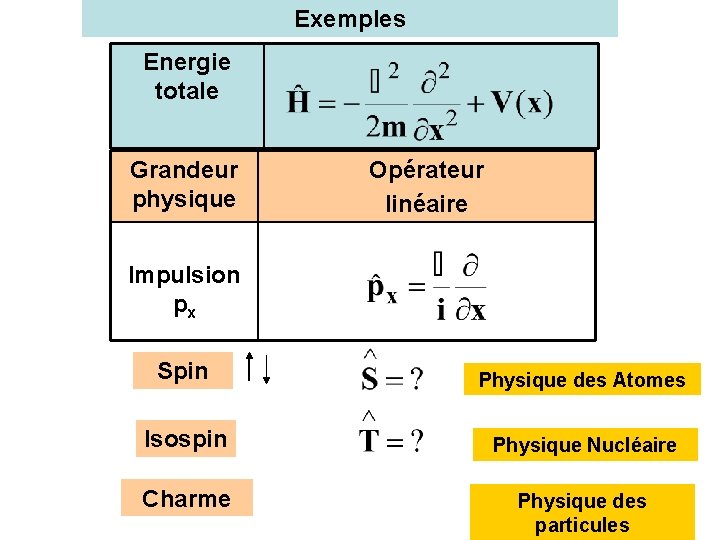
Exemples Energie totale Grandeur physique Opérateur linéaire Impulsion px Spin Physique des Atomes Isospin Physique Nucléaire Charme Physique des particules

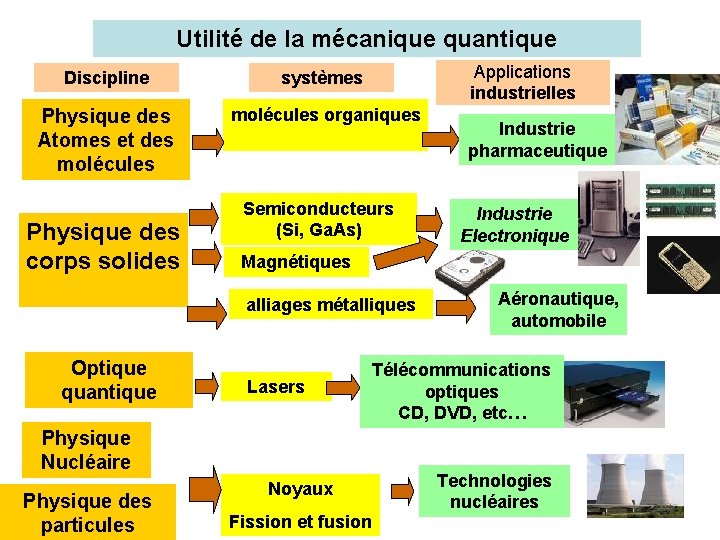
Utilité de la mécanique quantique Applications industrielles Discipline systèmes Physique des Atomes et des molécules organiques Physique des corps solides Semiconducteurs (Si, Ga. As) Lasers Physique Nucléaire Physique des particules Industrie Electronique Magnétiques alliages métalliques Optique quantique Industrie pharmaceutique Noyaux Fission et fusion Aéronautique, automobile Télécommunications optiques CD, DVD, etc… Technologies nucléaires

FIN

Bonne chance Auguri Boa sorte ¡ Buena suerte ! Желаю вам успеха. 祝您好运 Noroc bun Succes ! अलव द और शभक मन ए vận may Chúc may măn