Tirgul 6 Recursion 1 Recursion 2 What is

Tirgul 6 Recursion 1

Recursion 2

What is recursion? n n Similar to mathematical induction A recursive definition is self-referential A larger, more complex instance of a problem is defined in terms of a smaller, simpler instance of the same problem A base case must be defined explicitly 3

When do we use recursion? n n We are given a large problem (say of size n) We notice that: n n n There is some simple base case we know how to solve directly (say n=0) The solution to the large problem is composed of solutions to smaller problems of the same type If we could solve a smaller instance of the problem (say n-1), we could use that solution to solve the large problem 4

How do we use recursion? n n n A method may call itself Such a method is called recursive There must be some base case that is handled explicitly, without a recursive call The other case has to make sure there is progress towards the base case. The recursive method call will use simpler/smaller arguments 5

Recursive factorial n n n! = 1· 2· 3·…·n By definition, 0! = 1 (base case) Recursive definition: n! = (n-1)! · n For example: 4! = 3! · 4 = (2! · 3) · 4 = ((1! · 2) · 3) · 4 = (((0! · 1) · 2) · 3) · 4 = (((1 · 1) · 2) · 3) · 4 = 24 6

Recursive factorial public static int factorial(int n){ if (n == 0) { Base case return 1; } return n * factorial(n – 1); } recursive call 7

What’s happening here? 4· 6=24 i = factorial(4); 3· 2=6 factorial(3) 2· 1=2 factorial(2) 1· 1=1 int factorial(int n){ if (n == 0) return 1; return n*factorial(n– 1); } factorial(1) 1 factorial(0) 8

Recursion vs. loops n n We could have calculated factorial using a loop In general, loops are more efficient than recursion However, sometimes recursive solutions are much simpler than iterative ones Recursion can be a powerful tool for solving certain types of problems 9

Recursive addition n n We want to add two non-negative integers The only operations we are allowed to perform are +1 and -1 What’s the recursive formula? What’s the base case? What do you think? 10

Recursive addition public static int add(int a, int b){ if (b == 0) { return a; 3+4 = } 4+3 = return add(a+1, b-1); 5+2 = } 6+1 = 7+0 = 7 11

Recursive multiplication n n We want to multiply two non-negative integers The only operations we are allowed to perform are addition and subtraction What’s the recursive formula? What’s the base case? What do you think? 12

Recursive multiplication public static int multiply(int a, int b){ if (b == 0) { return 0; } 4 · 2 = return a + multiply(a, b-1); 4+4· 1 = } 4+4+4· 0 = 4+4+0 = 8 13

Recursive power n n Given an integer x and a non-negative integer n, we want to compute xn What’s the recursive formula? What’s the base case? What do you think? 14

Recursive power #1 public static int power(int x, int n){ if (n == 0) { 3 = 2 return 1; 2 = 2 · 2 } 1 = 2 · 2 return x * power(x, n-1); 2 · 2 · 2 0 = } 2 · 2 · 1 = What is the runtime 8 complexity of this method? 15

Complexity of recursive methods n n n When analyzing the complexity of recursive methods, we need to take into account how many recursive calls will be made (relative to the size of the input) When calculating xn, power is called n+1 times Each call takes a constant amount of time, so the runtime complexity is O(n) 16

Recursive power rethought n n n Recall that xa+b = xa · xb We can decompose the power n: n = 2(n / 2) + (n % 2) So we can “divide and conquer”: xn = x 2(n/2)+(n%2) = xn/2 · xn%2 17

Recursive power #2 public static int power(int x, int n){ if (n == 0) Why do we need return 1; two base cases? if (n == 1) return x; int tmp = power(x, n/2); return tmp * power(x, n%2); } Why do we use a temporary variable to store xn/2? 25 = 22· 21 = (21· 20)2· 21 = (2· 2· 1)2· 2 = 32 18

Recursive power #2 complexity n n How many times is power called when calculating xn? Note that power(x, n%2) is always a base case (n%2 is either 0 or 1) power(x, n) is computed using one call to power(x, n/2) So the runtime complexity is O(log n) 19

Recursively comparing arrays n n n We want to compare the contents of two given arrays Not allowed to use loops Recursive thinking: If we had a method for comparing arrays of length n-1, could we use it to compare arrays of length n? 20

Comparing arrays: The recursive helper method Returns true iff the given arrays are identical starting from the given index private static boolean compare(int[] a, int[] b, int index) { Base case 1: if (index == a. length) Reached the end of the arrays return true; Base case 2: if (a[index] != b[index]) Found one non equal number return false; return compare(a, b, index+1); } What are this method’s assumptions? 21

Comparing arrays: The public method Returns true iff the given arrays are identical. This method is not recursive! public static boolean compare(int[] a, int[] b) { if (a. length != b. length) return false; return compare(a, b, 0); } Call the recursive helper method with index 0 22

Recursively reversing arrays n n n We want to reverse a given array Not allowed to use loops Recursive thinking: We know the first and last elements need to be swapped. Then we only need to reverse the rest of the array… 23

Reversing an array: The recursive helper method Reverses the sub-array a[left…right] private static void reverse(int[] a, int left, int right){ if (left >= right) Base case return; int tmp = a[left]; a[left] = right; a[right] = tmp; reverse(a, left+1, right-1); } 24

Reversing an array: The public method Reverses the given array public static void reverse(int[] a){ reverse(a, 0, a. length-1); } Call the recursive helper method on the entire array 25

Converting to binary n n n We want to print the binary form of a given non-negative integer We divide the number by 2, and the remainder is the least significant bit We divide the resulting quotient by 2 again, and the remainder is the next bit… For example: 6/2 = 3(0) 3/2 = 1(1) 1/2 = 0(1) 26 So 6 = 110

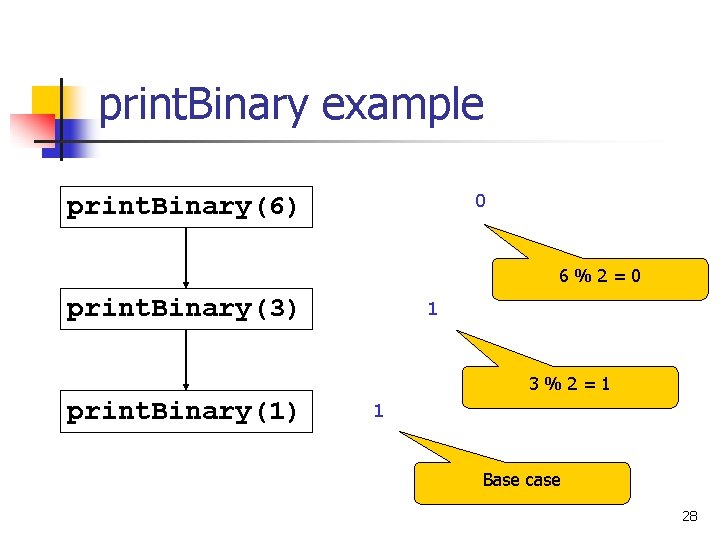
Converting to binary public static void print. Binary(int n){ if (n <= 1) { Base case: n is already in its binary form System. out. print(n); return; } print. Binary(n / 2); System. out. print(n % 2); } 27

print. Binary example 0 print. Binary(6) 6%2=0 print. Binary(3) 1 3%2=1 print. Binary(1) 1 Base case 28

Find the number of occurrences of ‘X’ in a String n n We want to find the number of occurrences of ‘X’ in a String What’s the recursive formula? What’s the base case? What do you think? 29

Find the number of occurrences of ‘X’ in a String public static int x. Length( String str ) { if ( str. equals( "" ) ) return 0; else if ( str. char. At(0) == 'X' ) return 1+x. Length(str. substring(1) ); else return 0+ x. Length(str. substring(1) ); } 30

Detect prime numbers n n We want to detect if a number is prime What’s the recursive formula? What’s the base case? What do you think? 31

Detect prime numbers public static int prime(int num) { return prime 2(num, num-1); } public static int prime 2( int num 1, int num 2 ) { if (num 2==1) return true; if ((num 1%num 2)==0) return false; else return prime 2(num 1, num 2 -1); } 32

Recursion tips n n n Think how to decompose a large problem into smaller instances of the same problem Solve the large problem assuming you have a solution to the smaller problems Don’t forget the base case It is often helpful to use a recursive helper method, and another method that “wraps” it There may be more than one recursive call in the same method Recursion may also be accomplished using two methods: f() calls g(), and g() calls f() 33

Mutual recursion example: Odd or Even // Is n an odd number public static boolean odd(int n){ if(n==1){ return true; } return even(n-1); } // Is n an even number public static boolean even(int n){ if(n==1){ return false; } return odd(n-1); } 34

The Fibonacci sequence n The Fibonacci sequence F(n) is defined as follows: n n n F(0) = 0 F(1) = 1 For n>1: F(n) = F(n-1) + F(n-2) 0, 1, 1, 2, 3, 5, 8, 13, 21, … We would like a method for computing F(n) 35

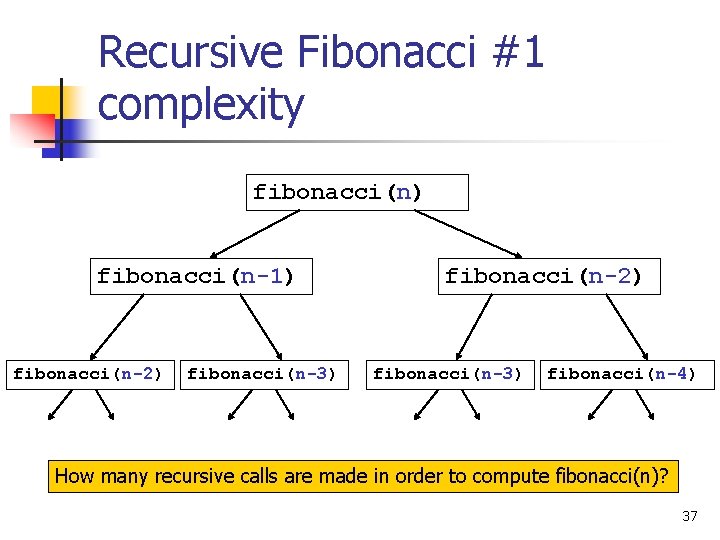
Recursive Fibonacci #1 public static int fibonacci(int n){ if (n==0 || n==1) return n; return fibonacci(n-1) + fibonacci(n-2); } What is the runtime complexity of this method? 36

Recursive Fibonacci #1 complexity fibonacci(n) fibonacci(n-1) fibonacci(n-2) fibonacci(n-3) fibonacci(n-4) How many recursive calls are made in order to compute fibonacci(n)? 37

Recursive Fibonacci #1 complexity n n n So we have a lower bound: T(n) = Ω(F(n)) But how does F(n) grow relative to n? There is actually a closed (non-recursive) formula: This implies that F(n) = Ω(1. 5 n) Conclusion: T(n) = Ω(1. 5 n) Can we do better? 38

Non-recursive Fibonacci public static int fibonacci(int n){ int f 1 = 0, f 2 = 1, f = f 1; for (int i=1; i<=n; i++){ f = f 1 + f 2; f 1 = f 2; f 2 = f; This iterative algorithm has runtime } complexity of O(n) return f; Is there a recursive solution in O(n)? } 39

Recursive Fibonacci #2 public static int fibonacci(int n){ if (n==0 || n==1) return n; return fibonacci(0, 1, 2, n); } private static int fibonacci(int f 1, int f 2, int index, int n){ int f = f 1 + f 2; if (index==n) return f; return fibonacci(f 2, f, index+1, n); } 40

Recursive Fibonacci #2 complexity n n This implementation is basically the same as the loop implementation index runs from 2 to n The recursive fibonacci method is called n-1 times The runtime complexity is O(n) 41

Recursive Fibonacci #3 public static int fibonacci(int n){ int[] f = new int[n+1]; f[0] = 0; if (n>0) f[1] = 1; return fibonacci(n, f); } private static int fibonacci(int n, int[] f){ if (n>1 && f[n]==0) f[n] = fibonacci(n-1, f)+fibonacci(n-2, f); return f[n]; } 42

Recursive Fibonacci #3 complexity n n We save the Fibonacci numbers we’ve already calculated in an array, to prevent duplicate work The recursion continues only if the array does not contain the number we need, and then the array is updated The runtime complexity is O(n) Notice it also has space complexity of O(n) 43

Backtracking 44

Backtracking – first example n n We can use recursion to go over many options, and do something for each case. Example: printing all subsets of the set S = {0, …, n-1} (printing the power set of S). Difficult to do with loops (but possible). Much simpler with recursion. 45

The basic idea - Power. Set n n Lets decompose the problem to two smaller problems of the same type. The recursive decomposition: n n n Print all subsets that contain an item, Then print all the subsets that do not contain it. Keep track of our current “state”. n n n items that are in the current subset, items not in the current subset, items we did not decide about yet. 46

Power. Set public class Power. Set { private boolean[] _set; public Power. Set(){} Holds the subset we are currently building. A default constructor that does nothing. private void print. Current. Set() { System. out. print("{ "); for(int i=0; i<_set. length; i++){ if(_set[i]) System. out. print(i + " "); } System. out. println("}"); }. . . 47 Prints the current subset

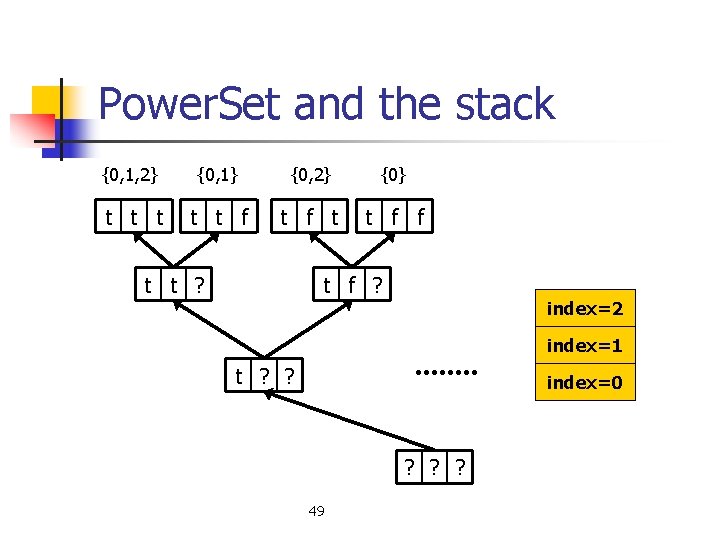
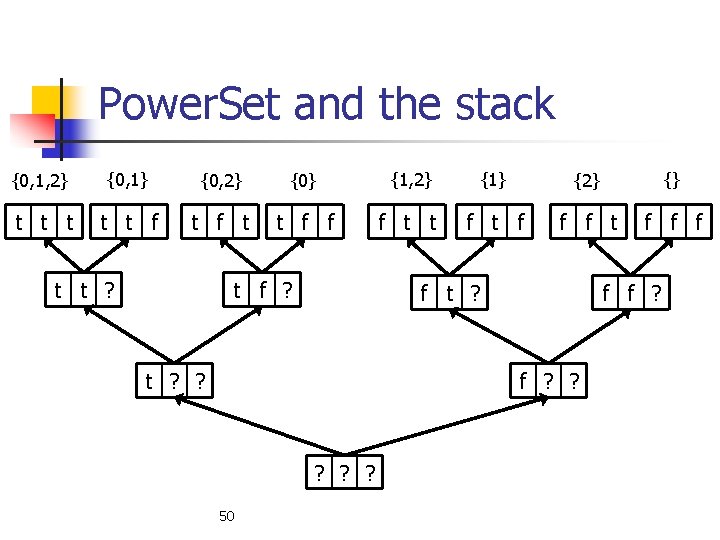
Power. Set (cont. ) public void print. Power. Set(int n){ _set = new boolean[n]; power. Set. Helper(0); _set = null; //free memory. } This is not the recursive method. It calls the recursive method that does the real work. private void power. Set. Helper(int index) { if(index==_set. length){ Base case: we picked out all the print. Current. Set(); items in the set – print it. return; } _set[index]=true; Print all sets that include index power. Set. Helper(index+1); _set[index]=false; power. Set. Helper(index+1); } Print all sets that exclude index

Power. Set and the stack {0, 1, 2} {0, 1} {0, 2} {0} t t t f f t t ? t f ? index=2 index=1 t ? ? index=0 ? ? ? 49

Power. Set and the stack {0, 1, 2} {0, 1} {0, 2} {0} {1, 2} {1} {2} {} t t t f f f t t f f f t t ? t f ? f t ? ? f f ? ? ? 50

Basics of Backtracking n n A backtracking alg. can be used to find a solution (or all solutions) to a combinatorial problem. Solutions are constructed incrementally If there are several options to advance incrementally, the algorithm will try one option, then backtrack and try more options. If you reach a state where you know the path will not lead you to the solution, backtrack! 51

N-Queens n The problem: n n n Simplifying step: n n On an Nx. N chess board, place N queens so that no queen threatens the other (no other queen allowed in same row, col or diagonal). Print only one such board. Place 1 queen somewhere in an available column then solve the problem of placing all other queens. Base case: n All queens have been placed. 52

The N-Queen Problem public class NQueens { private boolean[][] _board; public NQueens(){} to check if queen can be at row, col: private boolean illegal. Placement(int row, int col){…} public void place. Queens(int board. Size){ _board = new boolean[board. Size]; if(place. Queen. At. Col(0)){ This method uses a print. Board(); recursive helper method } that really does the work else{ System. out. println("No Placement Found!"); } _board = null; }

The N-Queen Problem private boolean place. Queen. At. Col(int col) { if(col == _board[0]. length){ Base case: we have return true; passed the last column. } for(int row=0; row<_board. length; row++){ if(illegal. Placement(row, col)){ Iterate over rows until it is okay to place a queen. continue; } Place the queen _board[row][col]=true; if(place. Queen. At. Col(col+1)){ Check if we can fill up the return true; remaining columns } If not, remove the queen _board[row][col]=false; and keep iterating. } If no placement works, return false; give up. }

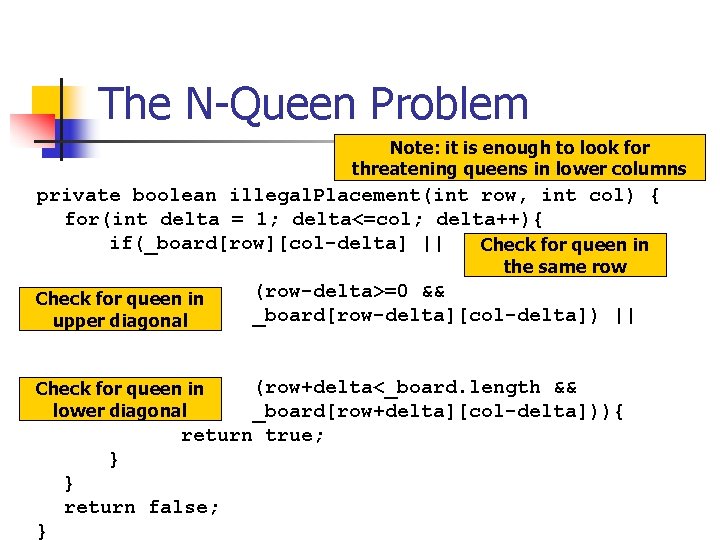
The N-Queen Problem Note: it is enough to look for threatening queens in lower columns private boolean illegal. Placement(int row, int col) { for(int delta = 1; delta<=col; delta++){ if(_board[row][col-delta] || Check for queen in the same row Check for queen in upper diagonal (row-delta>=0 && _board[row-delta][col-delta]) || (row+delta<_board. length && _board[row+delta][col-delta])){ return true; Check for queen in lower diagonal } } return false; }

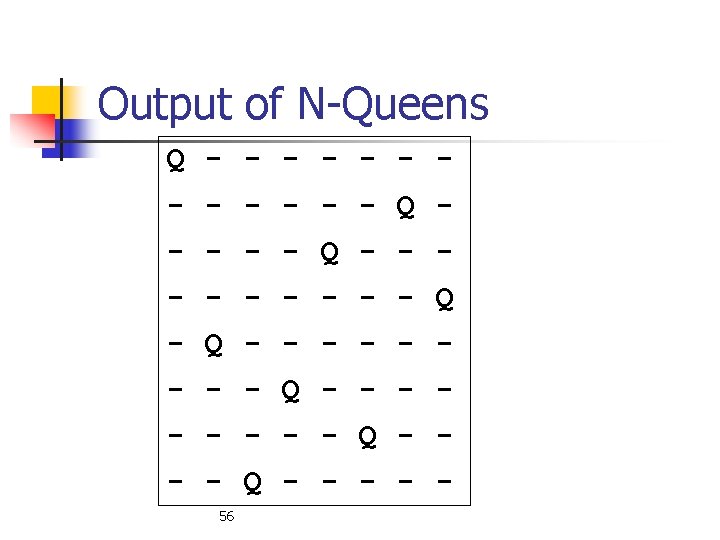
Output of N-Queens Q - Q 56 Q Q - Q - Q -

N-Queens: complexity n n Just to make sure: what is the runtime complexity of this N-Queens algorithm? Roughly lets regard the time to calculate place. Queen. At. Col with argument col: T(col). Although T(col, row) depend on the row also – there are some combinations that will be performed in O(1), but roughly, lets upper-bound it with T(col) There are N recursive calls to place. Queen. At. Col(col+1) from one call with col 57

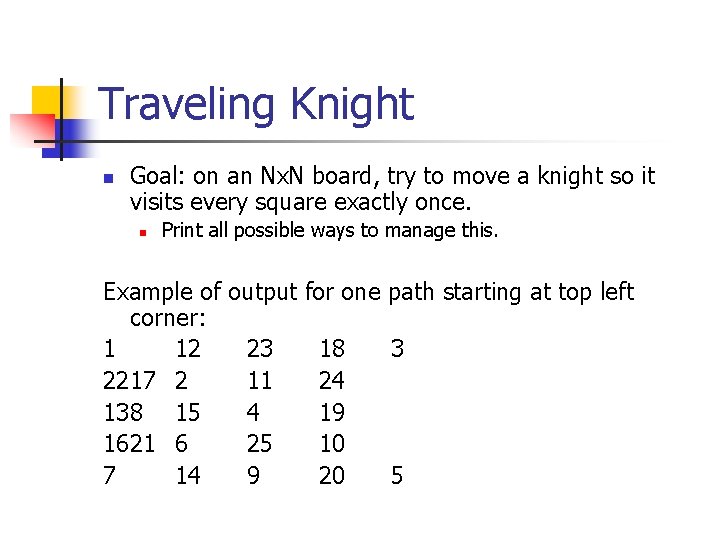
Traveling Knight n Goal: on an Nx. N board, try to move a knight so it visits every square exactly once. n Print all possible ways to manage this. Example of output for one path starting at top left corner: 1 12 23 18 3 2217 2 11 24 138 15 4 19 1621 6 25 10 7 14 9 20 5

Traveling Knight public class Traveling. Knight { private static final int[][] KNIGHT_MOVES = {{1, 2}, {2, 1}, {-1, 2}, {-2, 1}, {-1, -2}, {-2, -1}, {1, -2}, {2, -1}}; private int[][] _board; public Traveling. Knight(){} All possible moves The board An interface method that calls the private recursive one. public void travel(int board. Size, int row, int col){ _board = new int[board. Size]; travel. Helper(row, col, 1); }. . .

Traveling Knight private void travel. Helper(int row, int col, int step. Num){ _board[row][col] = step. Num; Do the move into this square if(step. Num==_board. length*_board[0]. length){ print. Board(); Base case: This is the last move } else{ for(int i=0; i<KNIGHT_MOVES. length; i++){ int new. Row = row+KNIGHT_MOVES[i][0]; int new. Col = col+KNIGHT_MOVES[i][1]; if(can. Go(new. Row, new. Col)) travel. Helper(new. Row, new. Col, step. Num+1); } Simplifying step: try each possible move. } _board[row][col] = 0; Backtrack -- Cancel } the move

Traveling Knight private boolean can. Go(int row, int col) { return (row>=0 && row<_board. length && col>=0 && col<_board[row]. length) && _board[row][col]==0; } Simply check if the square is in bounds and that we did not step in it already.

All Permutations n Goal: Print all permutations of the numbers 1…n Simplifying step? Base Case? . . . What do you think?

All Permutations private static void print. Array(int[] array) {…} private static void swap(int[] array, int i, int j) {…} public static void all. Permutations(int n){ int[] array = new int[n]; for(int i=0; i<n; i++){ An interface method. Inits the array and calls the array[i]=i+1; recursive method. } permutation. Helper(array, 0); }

All Permutations private static void permutation. Helper(int[] array, int ind) { if(ind==array. length){ print. Array(array); return; } Base Case: we selected the order of all elements in the array. Print it. for(int i=ind; i<array. length; i++){ Try out all options swap(array, ind, i); for placement in current index. permutation. Helper(array, ind+1); swap(array, ind, i); Note that when we } } backtrack we restore the array to its previous form

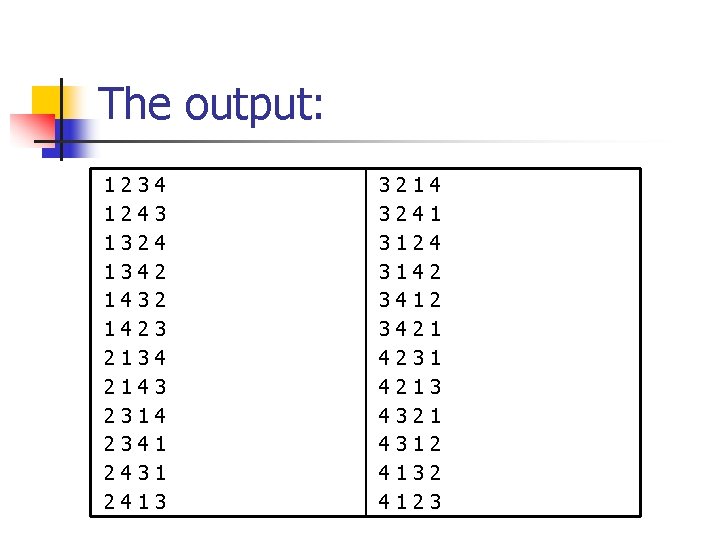
The output: 1 1 1 2 2 2 2 3 3 4 4 1 1 3 3 4 4 3 4 2 4 3 2 3 4 1 4 3 4 2 2 3 4 1 1 3 3 3 3 4 4 4 2 2 1 1 4 4 2 2 3 3 1 1 1 4 2 4 1 2 3 1 2 1 3 2 4 1 4 2 2 1 1 3 1 2 2 3