Recursion To understand recursion one must first understand



































![Recursive Binary Search boolean binary. Search(Item info[], Item item, int first, int last) { Recursive Binary Search boolean binary. Search(Item info[], Item item, int first, int last) {](https://slidetodoc.com/presentation_image_h/0498d93039ce83755f3ca300b701f7cc/image-38.jpg)




- Slides: 42

Recursion "To understand recursion, one must first understand recursion. " - Anonymous

What is Recursion? • Sometimes, the best way to solve a problem is by solving a smaller version of the exact same problem first. • Recursion is a technique that solves a problem by solving a smaller problem of the same type first. CS 221 - Computer Science II 2

Recursion • More than programming technique: • A way of describing, defining, or specifying things. • A way of designing solutions to problems (divide and conquer). CS 221 - Computer Science II 3

Basic Recursion 1. Base cases: – Always have at least one case that can be solved without using recursion. – Indicates an end to the recursion. 2. Make progress: – Any recursive call must make progress toward a base case. CS 221 - Computer Science II 4

Mathematical Examples There are recursive definitions for many mathematical problems: • • • Power Function Fibonacci Sequence Factorial Function CS 221 - Computer Science II 5

Power Function – The Power function yx : • Raise the number y to the xth power. – Assume x is a non-negative integer: CS 221 - Computer Science II 6

Power Function – The Power function yx : • Raise the number y to the xth power. – Assume x is a non-negative integer: yx = 1 if x is 0 // base case yx = y*y(x-1) otherwise // make progress CS 221 - Computer Science II 7

Power Function 23 = 2*22 CS 221 - Computer Science II 8

Power Function 23 = 2 * 22 22 = CS 221 - Computer Science II 9

Power Function 23 = 2 * 22 22 = 2 * 21 = CS 221 - Computer Science II 10

Power Function 23 = 2 * 22 22 = 2 * 21 = 2 * 20 = CS 221 - Computer Science II 11

Power Function 23 = 2 * 22 22 = 2 * 21 = 2 * 20 = 1 (Base Case) CS 221 - Computer Science II 12

Power Function 23 = 2 * 22 22 = 2 * 21 = 2 * 20 = 2 * 1 = 2 20 = 1 CS 221 - Computer Science II 13

Power Function 23 = 2 * 22 22 = 2 * 21 = 2 * 2 = 4 21 = 2 * 20 = 2 * 1 = 2 20 = 1 CS 221 - Computer Science II 14

Power Function 23 = 2 * 22 = 2 * 4 = 8 22 = 2 * 21 = 2 * 2 = 4 21 = 2 * 20 = 2 * 1 = 2 20 = 1 CS 221 - Computer Science II 15

Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … Fibonacci Function: Fib(0) = 1 // base case Fib(1) = 1 // base case Fib(n) = Fib(n-1) + Fib(n-2) // n>1 Unlike most recursive algorithms: § Two base cases, not just one. § Two recursive calls, not just one. CS 221 - Computer Science II 16

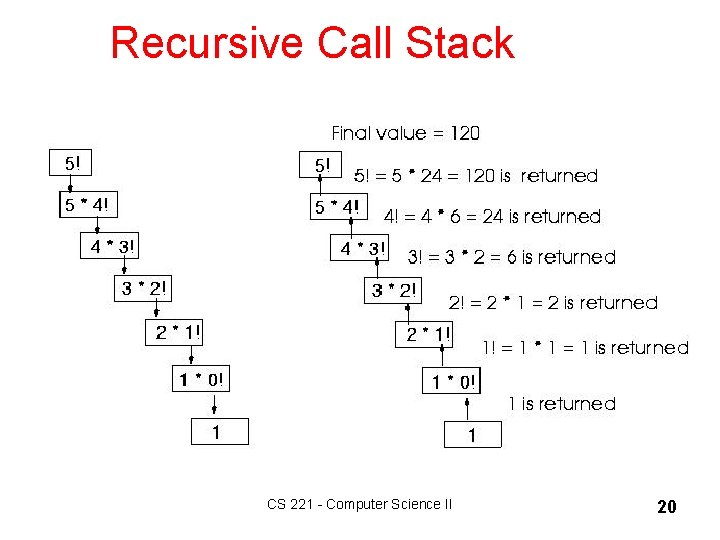
Factorial Function – factorial(0) = 1 // base case – factorial(n) = n * factorial(n-1) // n > 0 Compute factorial(3): CS 221 - Computer Science II 17

Factorial Function – factorial(0) = 1 // base case – factorial(n) = n * factorial(n-1) // n > 0 Compute factorial(3): factorial(3) = 3 * factorial(2) = 3 * ( 2 * factorial(1) ) = 3 * ( 2 * ( 1 * factorial(0) ) = 3 * ( 2 * ( 1 * 1 ) )) = 6 CS 221 - Computer Science II 18

Coding the Factorial Function Recursive Implementation int factorial(int n) { if (n==0) // base case return 1; else return n * factorial(n-1); } CS 221 - Computer Science II 19

Recursive Call Stack CS 221 - Computer Science II 20

Implementing Recursion What happens when a function gets called? // a method int b(int x) { int z, y; // other statements z = a(x) + y; return z; } // another method int a(int w) { return w+w; } CS 221 - Computer Science II 21

When a Function is Called § Stop executing function b. § To return to function b later, need to store everything about function b. § Create activation record. § Includes values of variables x, y, z. § The place to start executing when return. § Push activation record onto the call stack. § Then, a is bound to w from b. § Control is transferred to function a. CS 221 - Computer Science II 22

When a Function is Called 8 After function a is executed, the activation record is popped out off call stack. § Values of the parameters and variables in function b are restored. § Return value of function a replaces a(x) in the assignment statement. CS 221 - Computer Science II 23

Recursion Overhead § Space § Every invocation of a function call requires: § Space for parameters and local variables. § Space for return address. § Thus, a recursive algorithm needs space proportional to the number of nested calls to the same function. CS 221 - Computer Science II 24

Recursion Overhead § Time § Calling a function involves: § Allocating, and later releasing, local memory. § Copying values into the local memory for the parameters. § Branching to/returning from the function All contribute to the time overhead, which is generally exponential. CS 221 - Computer Science II 25

Recursion vs. Iteration § Recursion calls the same function over and over. § Recursive algorithms use a branching structure. § Iteration `jumps back' to the start of the loop. § Iterative algorithms use a looping construct. § Iteration can be used in place of recursion. § Recursive solutions are usually less efficient. § In terms of both time and space. § Usually exponential in both. § Recursion may simplify the solution. § Shorter, more easily understood source code. CS 221 - Computer Science II 26

Coding Factorial Function Iterative implementation: int factorial(int n) { int fact = 1; for(int count = 2; count <= n; count++) fact = fact * count; return fact; } CS 221 - Computer Science II 27

Other Recursive Examples Combinations n Euclid’s Algorithm n Binary Search n CS 221 - Computer Science II 28

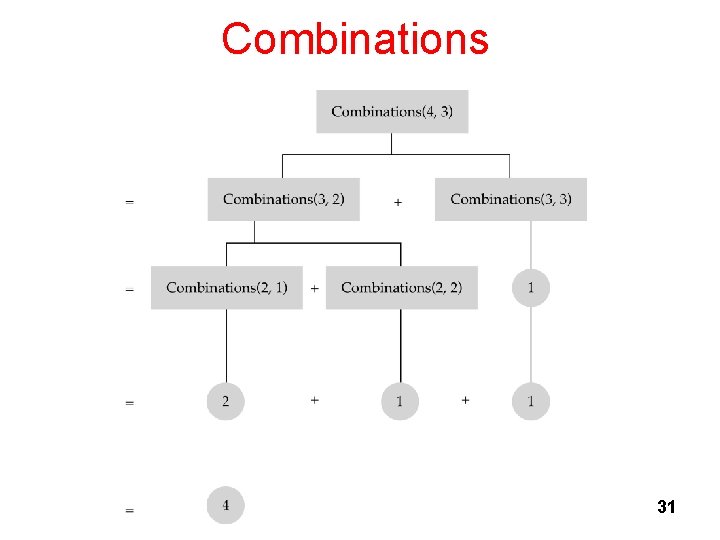
Combinations: n choose k Given n things, how many different sets of size k can be chosen? n n-1 = + k-1 , 1 < k < n (recursive solution) k k n n! = , 1 < k < n (closed-form solution) k k!(n-k)! with base cases: n n = n (k = 1), = 1 (k = n) 1 n Pascal’s Triangle CS 221 - Computer Science II 29

Combinations: n choose k int combinations(int n, int k) { if(k == 1) // base case 1 return n; else if (n == k) // base case 2 return 1; else return(combinations(n-1, k) + combinations(n-1, k 1)); } CS 221 - Computer Science II 30

Combinations 31

Euclid's Algorithm About 300 BC, Euclid wrote an algorithm to calculate the greatest common divisor (GCD) of two numbers x and y, where (x < y). This can be stated as: 1. Divide y by x with remainder r. 2. Replace y by x, and x with r. 3. Repeat step 1 until r is zero. When this algorithm terminates, y is the highest common factor. CS 221 - Computer Science II 32

GCD(34017, 16966) Euclid's algorithm works as follows: – 34, 017/16, 966 produces a remainder 85 – – 16, 966/85 produces a remainder 51 85/51 produces a remainder 34 51/34 produces a remainder 17 34/17 produces a remainder 0 The highest common divisor of 34, 017 and 16, 966 is 17. CS 221 - Computer Science II 33

Writing a Recursive Function 1. Determine the base case(s). – Can solve without recursion. 2. Determine the general case(s). – Express solution as a smaller version of itself. 3. Verify the algorithm. – Use the "Three-Question-Method. " CS 221 - Computer Science II 34

Three-Question Method 1. The Base-Case Question: Is there a non-recursive way out of the function, and does the routine work correctly for this "base" case? 2. The Smaller-Caller Question: Does each recursive call to the function involve a smaller case of the original problem, leading inescapably to the base case? 3. The General-Case Question: Assuming that the recursive call(s) work correctly, does the whole function work correctly? CS 221 - Computer Science II 35

Binary Search § Search algorithm § Finds a target value within a sorted list. § Compares target value to the middle element. § If the two are equal, done. § If target less than middle element, search lower half of list. Otherwise, search upper half of list. § Continue dividing list in half until find target or run out of list to search. § Efficiency: § Runs in at worst logarithmic O(log n) time. § Takes up linear O(n) space. CS 221 - Computer Science II 36

Recursive Binary Search What are the base cases? 1. If first > last, return false 2. If item==info[mid. Point], return true What is the general case? if item < info[mid. Point] // search the first half if item > info[mid. Point], //search the second half CS 221 - Computer Science II 37
![Recursive Binary Search boolean binary SearchItem info Item item int first int last Recursive Binary Search boolean binary. Search(Item info[], Item item, int first, int last) {](https://slidetodoc.com/presentation_image_h/0498d93039ce83755f3ca300b701f7cc/image-38.jpg)
Recursive Binary Search boolean binary. Search(Item info[], Item item, int first, int last) { int mid. Point; if(first > last) // base case 1 return false; else { mid. Point = (first + last)/2; if (item == info[mid. Point]) // base case 2 { item = info[mid. Point]; return true; } else if(item < info[mid. Point]) return binary. Search(info, item, first, mid. Point-1); else return binary. Search(info, item, mid. Point+1, last); } } CS 221 - Computer Science II 38

When to Use Recursion § When the depth of recursive calls is relatively "shallow. " § The recursive version does about the same amount of work as the nonrecursive version. § The recursive version is shorter and simpler than the non-recursive solution. CS 221 - Computer Science II 39

Benefits of Recursion § Recursive functions are clearer, simpler, shorter, and easier to understand than their non-recursive counterparts. § The program directly reflects the abstract solution strategy (algorithm). § Reduces the cost of maintaining the software. CS 221 - Computer Science II 40

Disadvantages of Recursion § Makes it easier to write simple and elegant programs, but it also makes it easier to write inefficient ones. § Use recursion to ensure correctness, not efficiency. § Simple, elegant recursive algorithms are inherently inefficient. CS 221 - Computer Science II 41

CS 221 - Computer Science II 42
 To understand recursion you must understand recursion
To understand recursion you must understand recursion We must first seek to understand
We must first seek to understand In order to understand recursion
In order to understand recursion I must become less
I must become less Listen or thy tongue will make thee deaf
Listen or thy tongue will make thee deaf The deepest need of the human heart is to be understood
The deepest need of the human heart is to be understood Self-centered listening
Self-centered listening Self-centered listeners
Self-centered listeners Habit no 5
Habit no 5 Seek first to understand then to be understood summary
Seek first to understand then to be understood summary One empire one god one emperor
One empire one god one emperor One one little dog run
One one little dog run One king one law one faith
One king one law one faith One god one empire one emperor
One god one empire one emperor One ford
One ford See one do one teach one
See one do one teach one One price policy
One price policy Twelfth night speeches
Twelfth night speeches Studiendekanat uni bonn
Studiendekanat uni bonn One vision one identity one community
One vision one identity one community One vision one identity one community
One vision one identity one community God's covenant
God's covenant The first person that we must see is mr.smith
The first person that we must see is mr.smith To be free one must be chained
To be free one must be chained Iambic pentameter othello
Iambic pentameter othello Othello poetry vs prose
Othello poetry vs prose Bishop must be husband of one wife
Bishop must be husband of one wife If one aircraft wishes to overtake another it must
If one aircraft wishes to overtake another it must Cadet rule
Cadet rule Then must you speak of one that loved
Then must you speak of one that loved You must choose one
You must choose one Then must you speak of one that loved
Then must you speak of one that loved Maturity continuum model victories order
Maturity continuum model victories order Breadth first search
Breadth first search Sdl first vs code first
Sdl first vs code first Put first things first activities
Put first things first activities Habit 3 first things first
Habit 3 first things first Difference between code first and database first approach
Difference between code first and database first approach First to invent or first to file
First to invent or first to file First in first out
First in first out![Stack=[] digunakan untuk memebuat stack dengan Stack=[] digunakan untuk memebuat stack dengan](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20200%20200%22%3E%3C/svg%3E) Stack=[] digunakan untuk memebuat stack dengan
Stack=[] digunakan untuk memebuat stack dengan First in first out
First in first out First come first serve
First come first serve








































![Stack=[] digunakan untuk memebuat stack dengan Stack=[] digunakan untuk memebuat stack dengan](https://slidetodoc.com/wp-content/uploads/2020/10/1003988_042512bb86e3aab910dfb86ac5697e60-300x212.jpg)