Recursion Canonical example factorial l Recursion l l

Recursion

Canonical example: factorial l Recursion l l Classical example – the factorial function l l When a method calls itself n! = 1· 2· 3· ··· · (n-1)· n Recursive definition

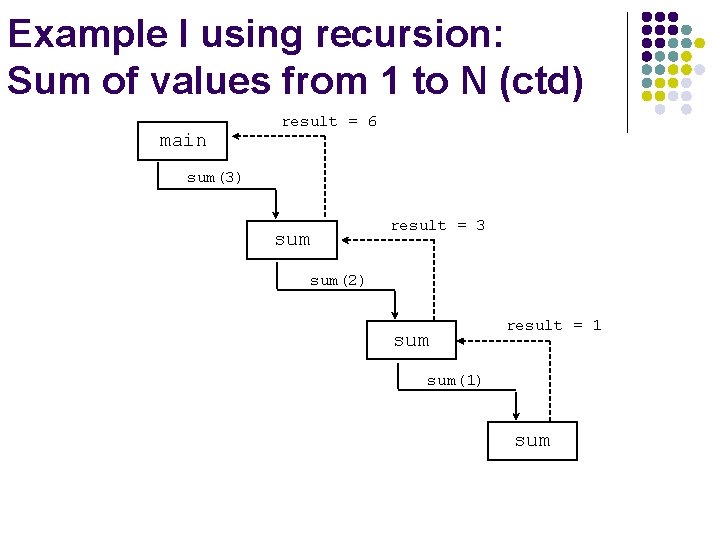
Example I using recursion: Sum of values from 1 to N l Problem l l computing the sum of all the numbers between 1 and N This problem can be recursively defined as:

Example I using recursion: Sum of values from 1 to N (ctd) // This method returns the sum of 1 to num // Refer to Sum. App project public int sum (int num) { int result; if (num == 1) result = 1; else result = num + sum (n-1); return result; }

Example I using recursion: Sum of values from 1 to N (ctd) main result = 6 sum(3) sum result = 3 sum(2) sum result = 1 sum(1) sum

Content of recursive definition l Base case (s) l Values of the input variables for which l l Every chain of recursive calls must l l no recursive calls are performed § There should be at least one base case Eventually reach a base case Recursive calls l Calls to the current method l Defined in such a way that l It makes progress towards a base case

Example II using recursion: Factorial l Factorial of a positive integer n, written n! is the product l l l n · (n – 1) · (n – 2) · … · 1 with 1! equal to 1 and 0! defined to be 1 The factorial of integer number can be calculated l iteratively (non-recursively) using a for statement as follows: l l l factorial = 1; for(int counter = number; counter >= 1; counter-- ) factorial *= counter; Recursive declaration of the factorial method is arrived at l by observing the following relationship: l n! = n · (n – 1)!

Example II using recursion: Factorial (cont’d) l long should be used so that the program l l can calculate factorials greater than 12! Package java. math provides classes l Big. Integer and Big. Decimal explicitly for l l high precision calculations not supported by primitive types. Refer to Factorial. App project

Example II using recursion: Factorial (cont’d) l Big. Integer method compare. To l compares the Big. Integer that calls the method to l l the method’s Big. Integer argument. Returns l -1 if the Big. Integer that calls the method is less than the argument, 0 if they are equal or 1 if the Big. Integer that calls the method § is greater than the argument. § l l l Big. Integer constant l l ONE represents the integer value 1. ZERO represents the integer value 0.

Example III using recursion: Fibonacci Series l The Fibonacci series, begins with 0 and 1 and l has the property that each subsequent Fibonacci number l l The ratio of successive Fibonacci numbers converges to l a constant value of 1. 618…, l l is the sum of the previous two. § 0, 1, 1, 2, 3, 5, 8, 13, 21, … called the golden ratio or the golden mean. The Fibonacci series may be defined recursively: l fibonacci(0) = 0 fibonacci(1) = 1 fibonacci(n) = fibonacci(n– 1) + fibonacci(n– 2)

Example III using recursion: Fibonacci Series l Two base cases for Fibonacci method l l l fibonacci(0) is defined to be 0 fibonacci(1) to be 1 Fibonacci numbers tend to become large quickly. l We use type Big. Integer as the return type of l l Big. Integer methods multiply and subtract l l The fibonacci method implement multiplication and subtraction. Refer to Fibonacci. App project

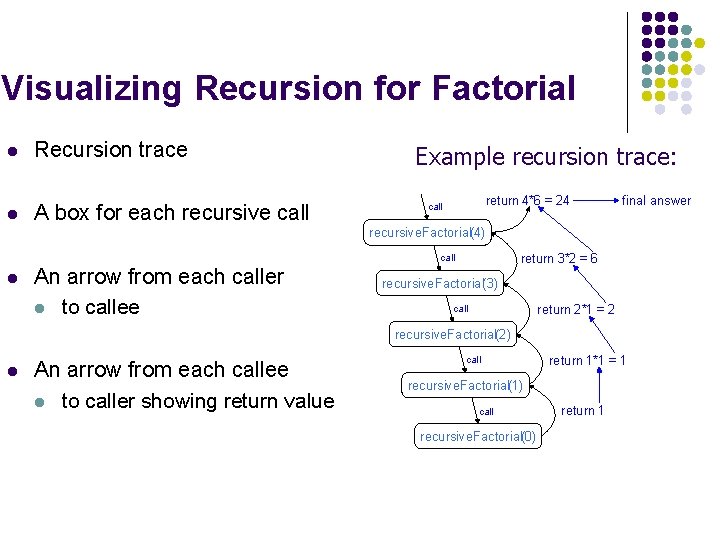
Visualizing Recursion for Factorial l Recursion trace l A box for each recursive call Example recursion trace: return 4*6 = 24 call final answer recursive. Factorial(4) return 3*2 = 6 call l An arrow from each caller l to callee recursive. Factorial(3) return 2*1 = 2 call recursive. Factorial(2) l An arrow from each callee l to caller showing return value call return 1*1 = 1 recursive. Factorial(1) call recursive. Factorial(0) return 1

Example IV using recursion: Binary Search l A binary search l Assumes the list of items in the search pool is sorted l Eliminates a large part of search pool with 1 comparison l Examines the middle element of the list l If it matches the target, the search is over l Otherwise, only one half of the remaining elements § Need to be searched l Then examines the middle element of remaining pool l Eventually, the target is found or data is exhausted

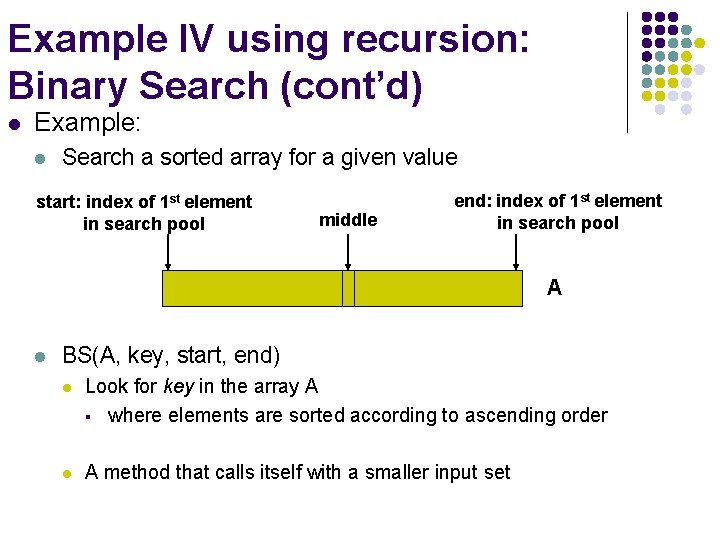
Example IV using recursion: Binary Search (cont’d) l Example: l Search a sorted array for a given value start: index of 1 st element in search pool middle end: index of 1 st element in search pool A l BS(A, key, start, end) l Look for key in the array A § where elements are sorted according to ascending order l A method that calls itself with a smaller input set

Binary search recursion: pseudocode // Refer to Binary. Search. App project Boolean BS(A, key, start, end) mid = (start+end)/2 if(A[mid] == key) return true else if(end <= start) return false else if (A[mid] > key) return BS(A, key, start, mid-1) else return BS(A, key, mid+1, end)

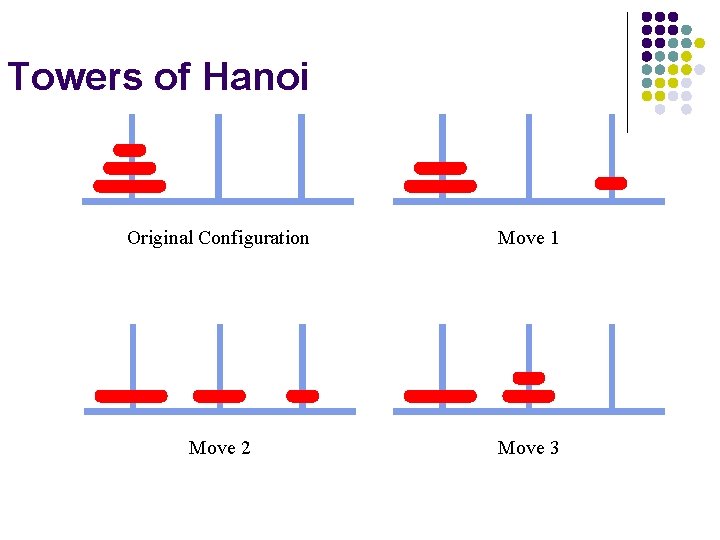
Example V using recursion: Towers of Hanoi l l Given l A platform with three pegs sticking out of it l Each peg is a stack that can accommodate n disks l Puzzle l Move all disks from peg a to peg c, one disk at a time l So that we never place a larger disk on top of smaller one Refer to Towers. Of. Hanoi. App project

Towers of Hanoi Original Configuration Move 1 Move 2 Move 3

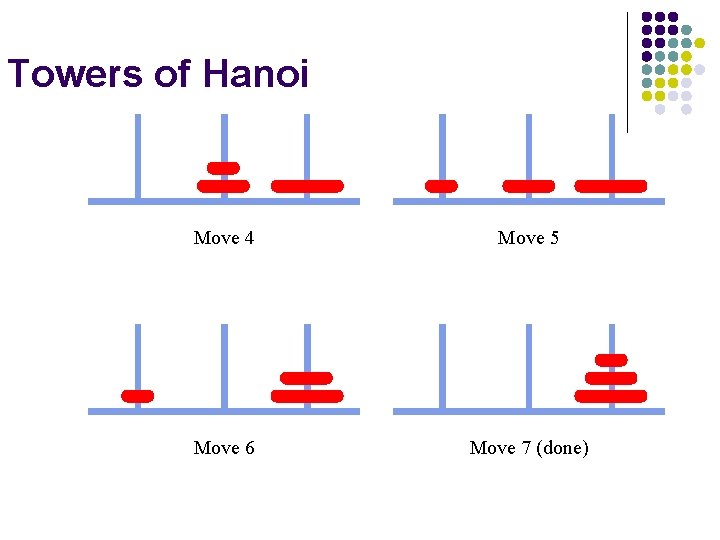
Towers of Hanoi Move 4 Move 5 Move 6 Move 7 (done)