Threshold Phenomena and Fountain Codes Amin Shokrollahi EPFL

Threshold Phenomena and Fountain Codes Amin Shokrollahi EPFL Parts are joint work with M. Luby, R. Karp, O. Etesami

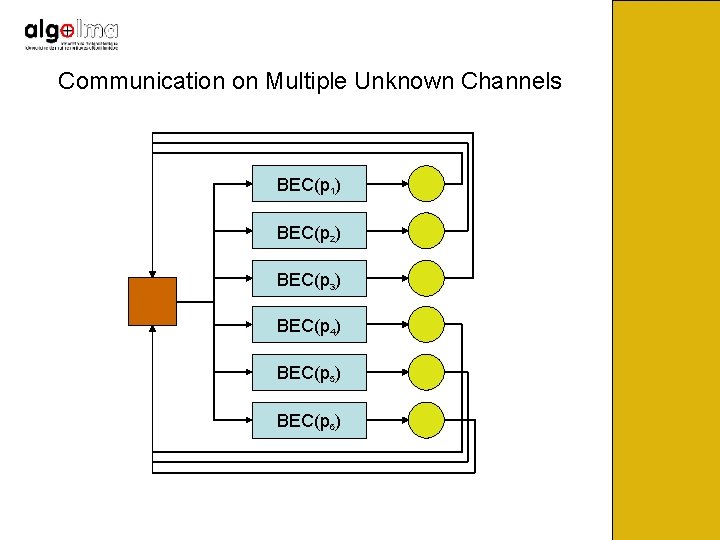
Communication on Multiple Unknown Channels BEC(p 1) BEC(p 2) BEC(p 3) BEC(p 4) BEC(p 5) BEC(p 6)

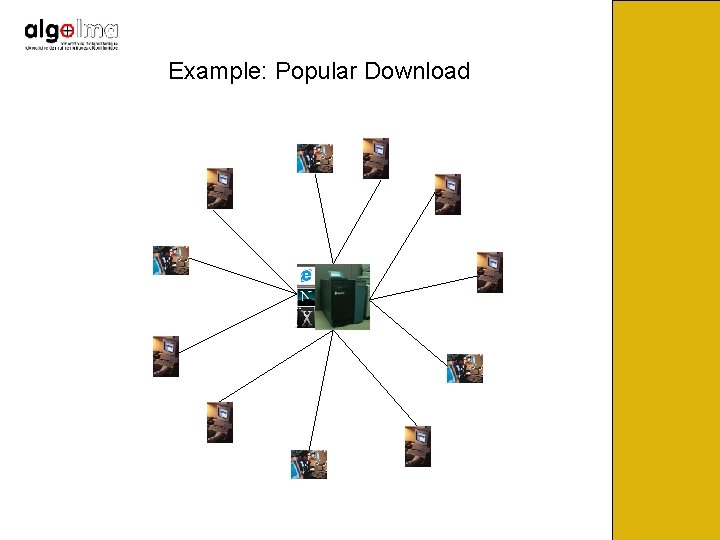
Example: Popular Download

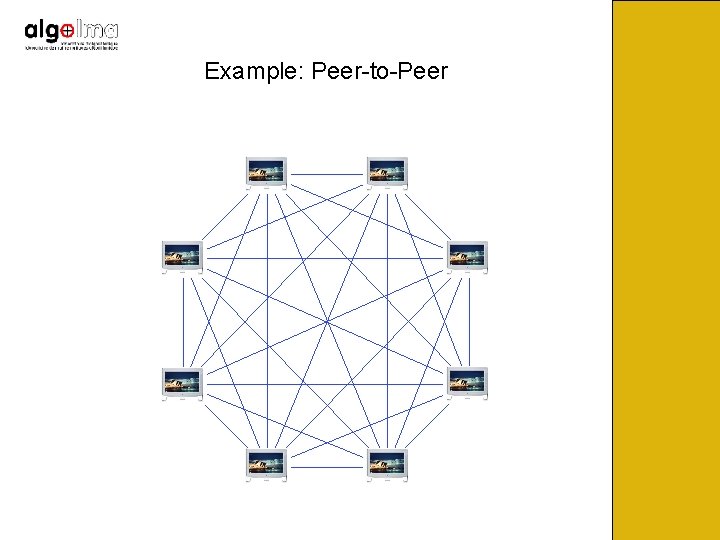
Example: Peer-to-Peer

Example: Satellite

The erasure probabilities are unknown. Want to come arbitrarily close to capacity on each of the erasure channels, with minimum amount of feedback. Traditional codes don’t work in this setting since their rate is fixed. Need codes that can adapt automatically to the erasure rate of the channel.

What we Really Want Original content Users reconstruct Original content as soon as they receive enough packets Transmission Encoding Engine Encoded packets Reconstruction time should depend only on size of content

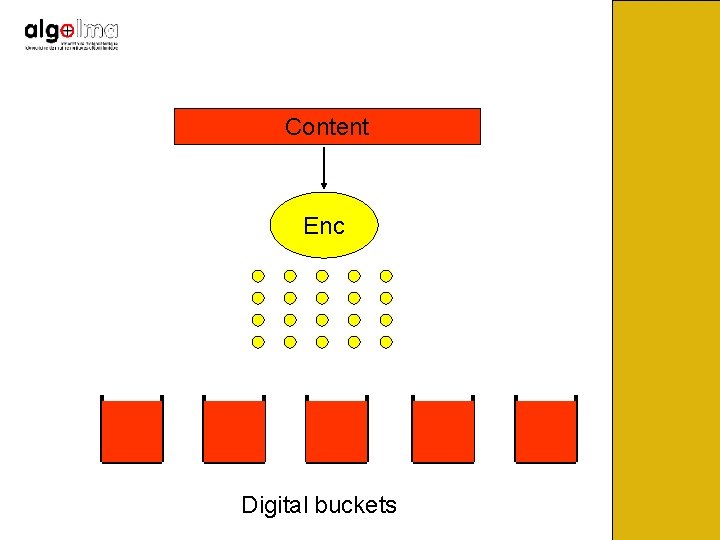
Content Enc Digital buckets

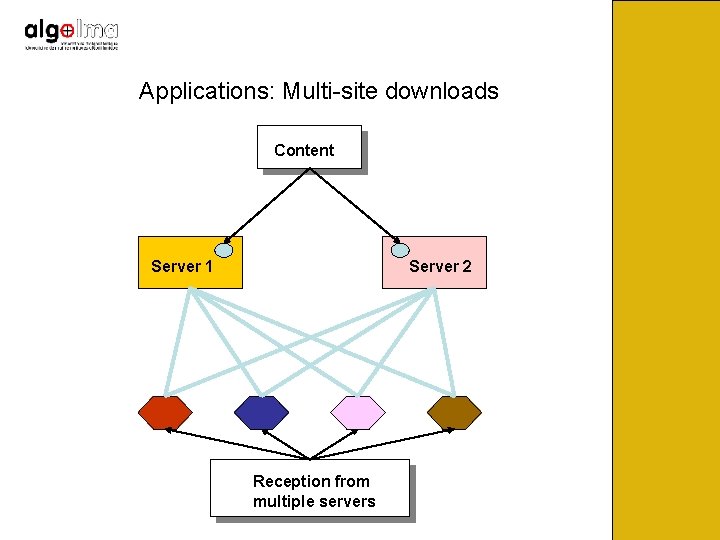
Applications: Multi-site downloads Content Server 1 Server 2 Reception from multiple servers

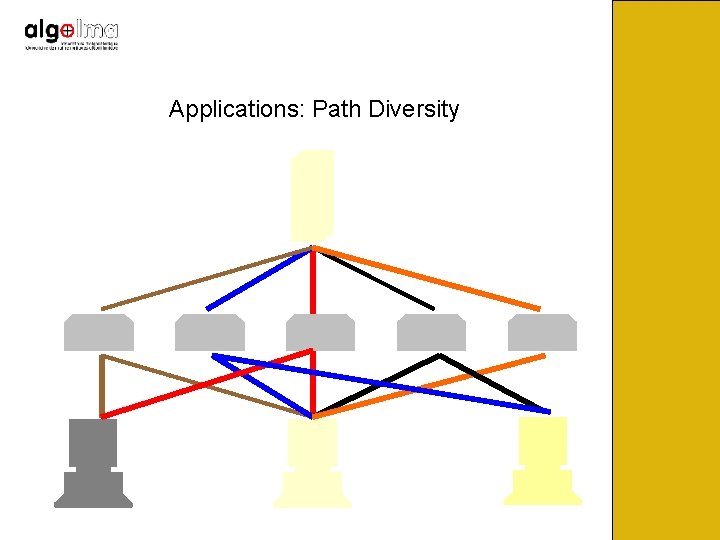
Applications: Path Diversity

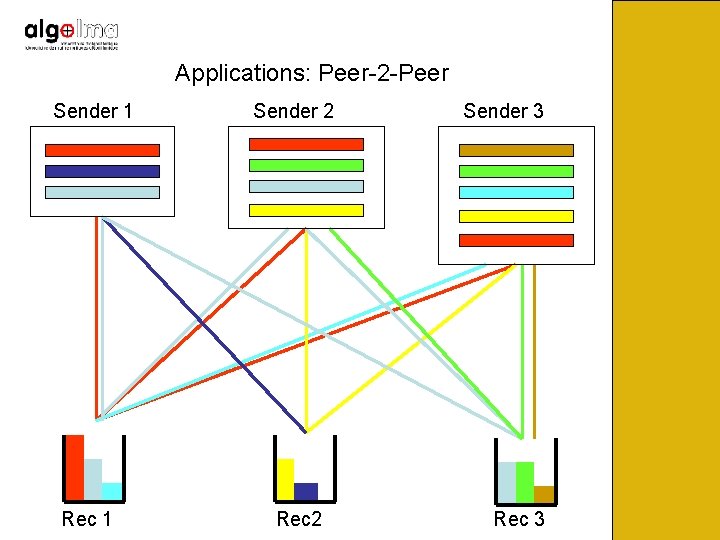
Applications: Peer-2 -Peer Sender 1 Rec 1 Sender 2 Rec 2 Sender 3 Rec 3

Fountain Codes Sender sends a potentially limitless stream of encoded bits. Receivers collect bits until they are reasonably sure that they can recover the content from the received bits, and send STOP feedback to sender. Automatic adaptation: Receivers with larger loss rate need longer to receive the required information. Want that each receiver is able to recover from the minimum possible amount of received data, and do this efficiently.

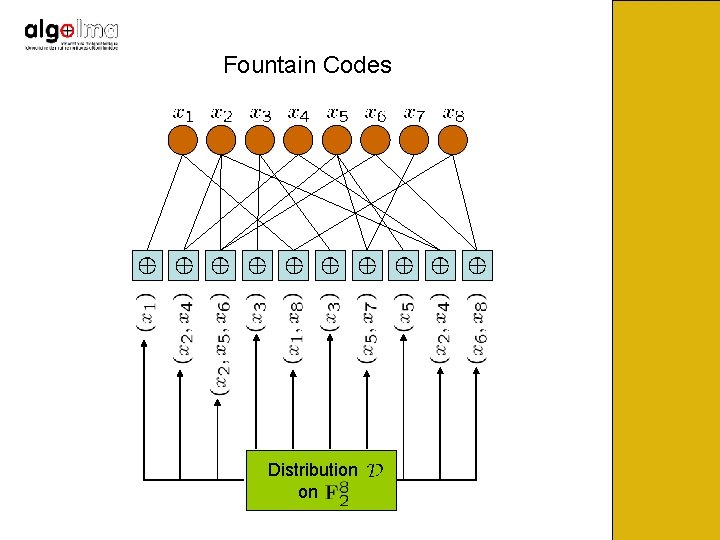
Fountain Codes Fix distribution symbols. on , where is number of input For every output symbol sample independently from and add input symbols corresponding to sampled subset.

Fountain Codes Distribution on

Universality and Efficiency [Universality] Want sequences of Fountain Codes for which the overhead is arbitrarily small [Efficiency] Want per-symbol-encoding to run in close to constant time, and decoding to run in time linear in number of output symbols.

Parameters • Overhead is the fraction of extra symbols needed by the receiver as compared to the number of input symbols (i. e. if k(1+ε) is needed , overhead =ε) – want to be arbitrarily small • Cost of encoding and decoding – linear in k • Ratelessness – the number of output symbols is not determined apriori • Space considerations (less important)

LT-Codes • Invented by Michael Luby in 1998. • First class of universal and almost efficient Fountain Codes • Output distribution has a very simple form • Encoding and decoding are very simple

LT-Codes LT-codes use a restricted distribution on Fix distribution Distribution where on is given by is the Hamming weight of Parameters of the code are :

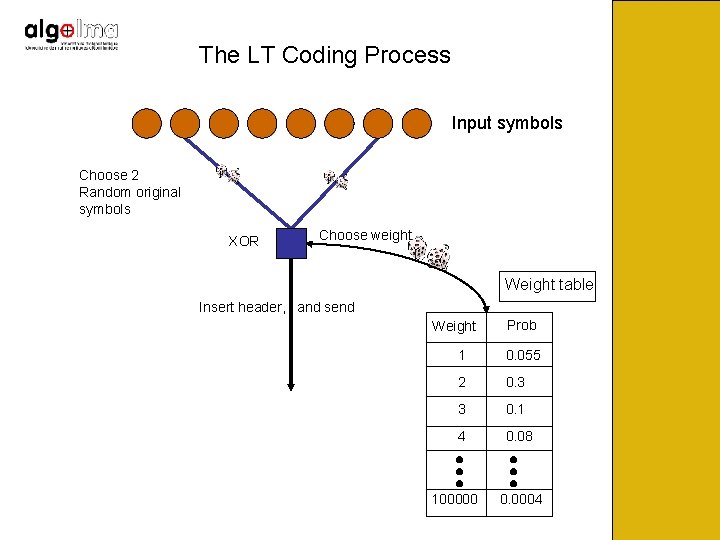
The LT Coding Process Input symbols Choose 2 Random original symbols XOR 2 Choose weight Weight table Insert header, and send Weight Prob 1 0. 055 2 0. 3 3 0. 1 4 0. 08 100000 0. 0004

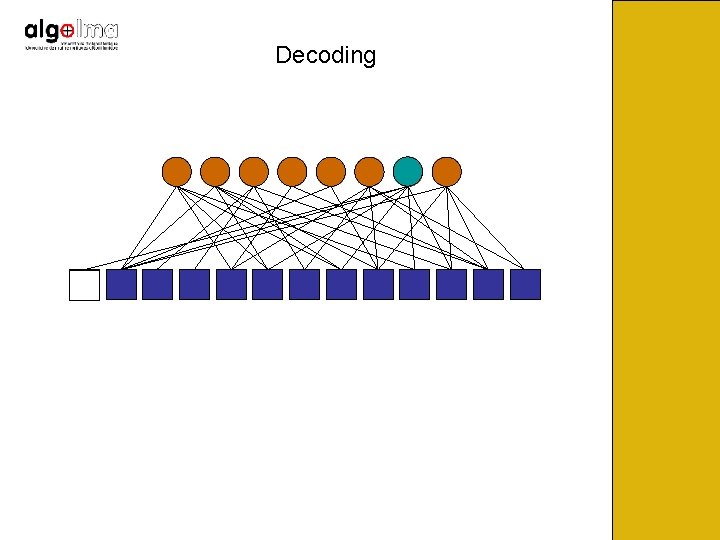
Decoding

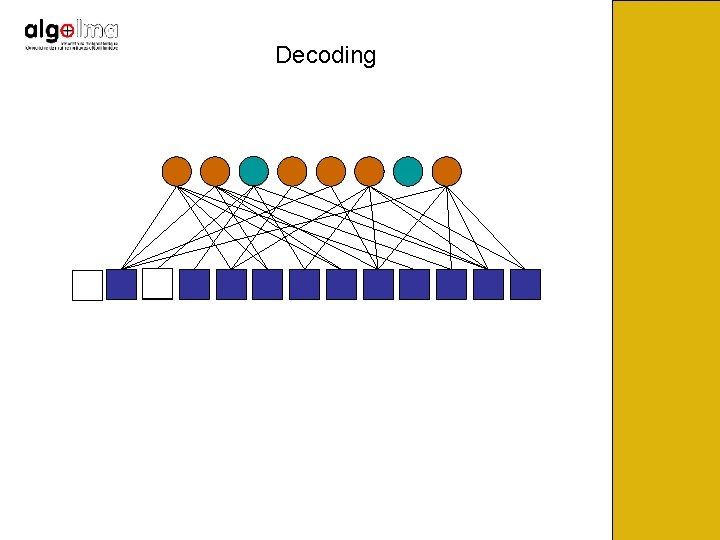
Decoding

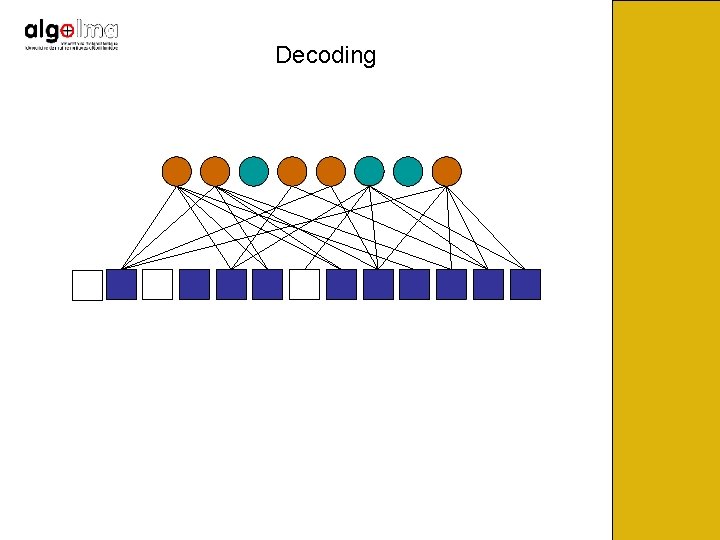
Decoding

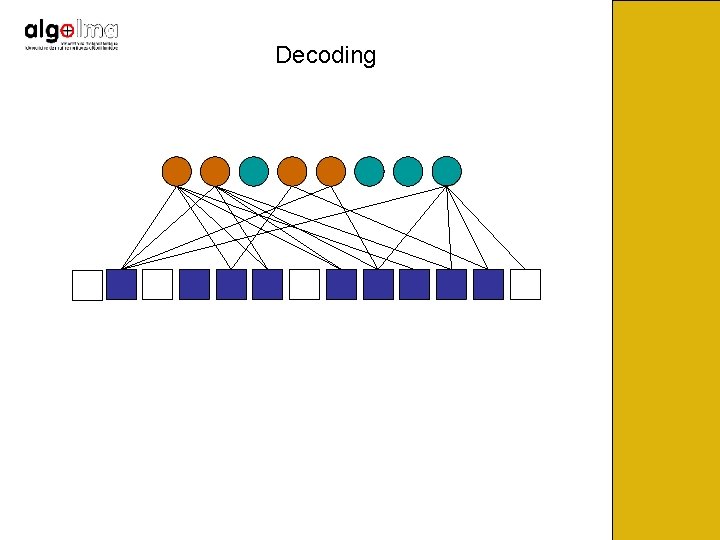
Decoding

Decoding

Decoding

Decoding

Decoding

Decoding

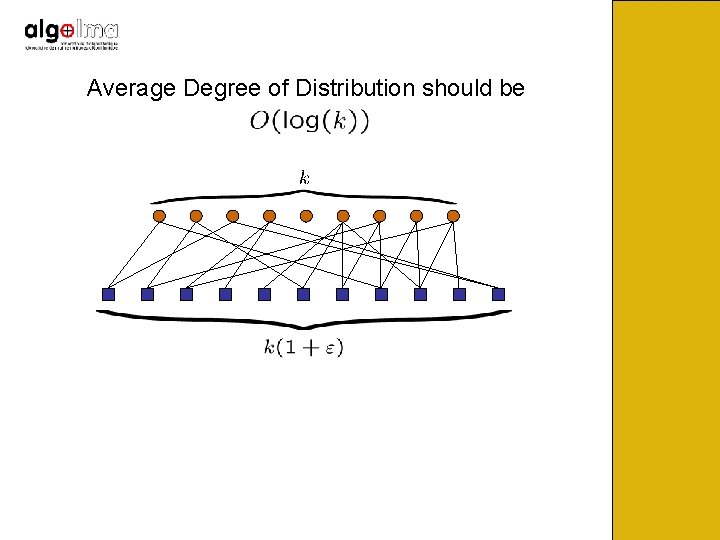
Average Degree of Distribution should be

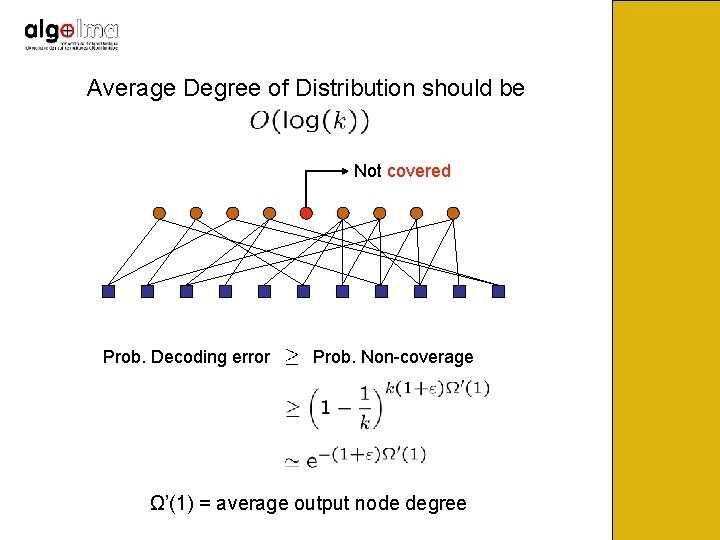
Average Degree of Distribution should be Not covered Prob. Decoding error Prob. Non-coverage Ω’(1) = average output node degree

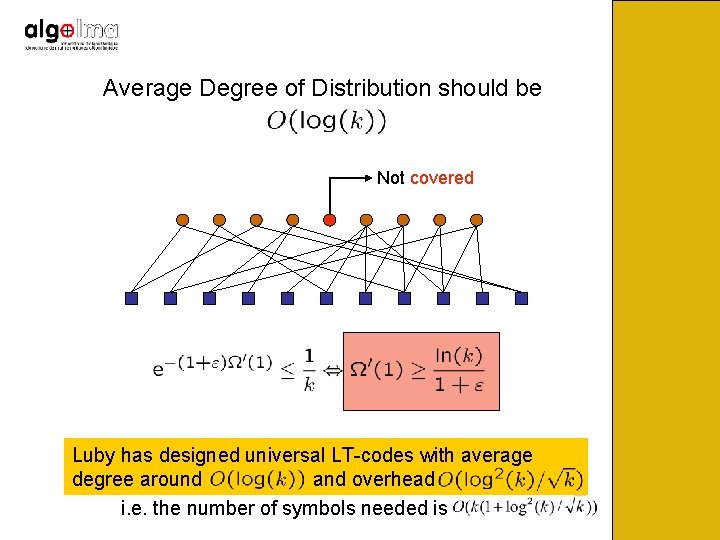
Average Degree of Distribution should be Not covered Luby has designed universal LT-codes with average degree around and overhead i. e. the number of symbols needed is

So: Average degree constant means error probability constant How can we achieve constant workload per output symbol, and still guarantee vanishing error probability? Raptor codes achieve this!

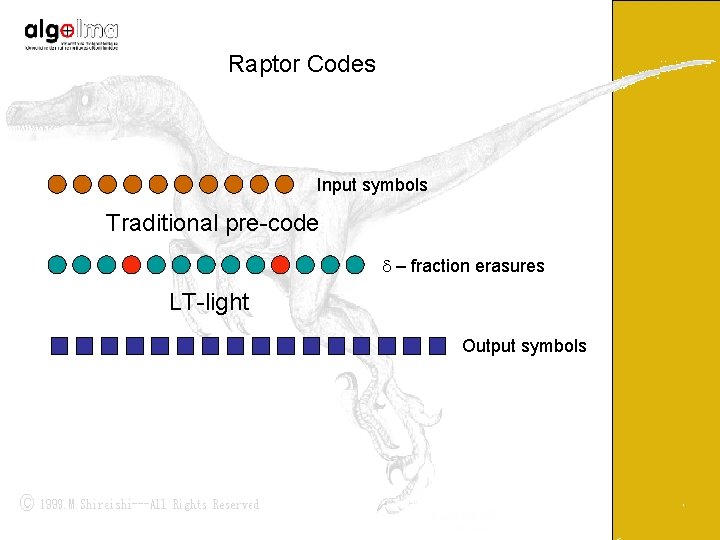
Raptor Codes • Use 2 phases: – pre-code encodes k input symbols into intermediate code – Apply LT to encode the intermediate code and transmit • The LT-decoder only needs to recover (1 -δ)n of the intermediate code w. h. p. This only requires constant degree!

Raptor Codes Input symbols Traditional pre-code d – fraction erasures LT-light Output symbols

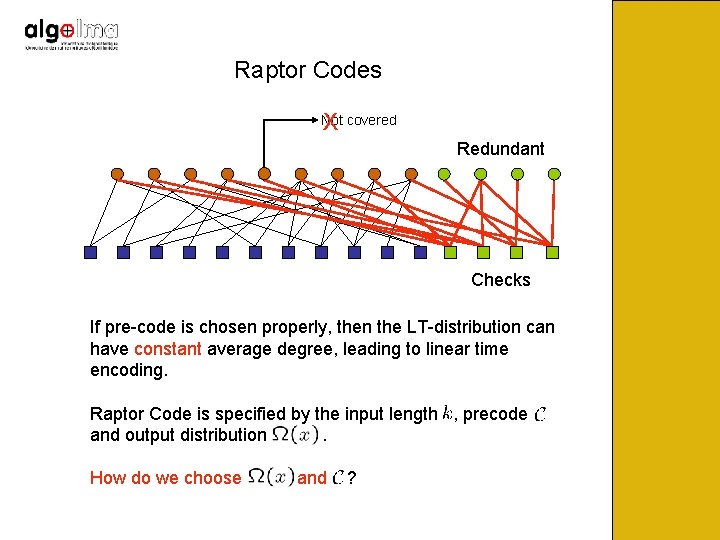
Raptor Codes X Not covered Redundant Checks If pre-code is chosen properly, then the LT-distribution can have constant average degree, leading to linear time encoding. Raptor Code is specified by the input length , precode and output distribution. How do we choose and ?

Special Raptor Codes: LT-Codes are Raptor Codes with trivial pre-code: Need average degree LT-Codes compensate for the lack of the pre-code with a rather intricate output distribution.

LT-lite • Max degree • Degree distribution: • Average Degree: • W. h. p can decode

What about pre-code? • Can use regular LDPC codes such as Tornado, right-regular code, etc. • But they have high average degree distributions…

Key Point • An LDPC code can be systematic (I. e. input symbols appear in the set of the output symbols) • Code rate (k/n) is arbitrarily close to 1, so most intermediate symbols have degree 1

Conclusions • Encoding and Decoding can be done in time linear in k (or constant time per input symbol) • The overhead is arbitrarily small as in regular LT codes • Storage requirement is just the stretch factor n/k and k is arbitrarily close to n

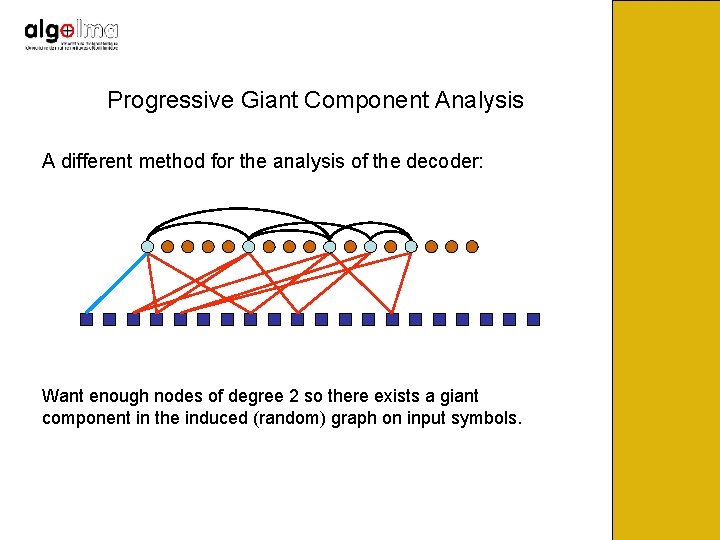
Progressive Giant Component Analysis A different method for the analysis of the decoder: Want enough nodes of degree 2 so there exists a giant component in the induced (random) graph on input symbols.

Progressive Giant Component Analysis First giant component removes symbols. -fraction of input Residual distribution: Fraction of residual nodes of degree 2: Average degree of new induced graph: Condition: “Ideal distribution: ”

Progressive Giant Component Analysis does not use “tree-assumption”, but only properties of induced graph. Analysis can be used to obtain error bounds for the decoding algorithm. It can also be used to obtain capacity-achieving distributions on the erasure channel. A modified version can be used to obtain for capacityachieving distributions for other symmetric channels.

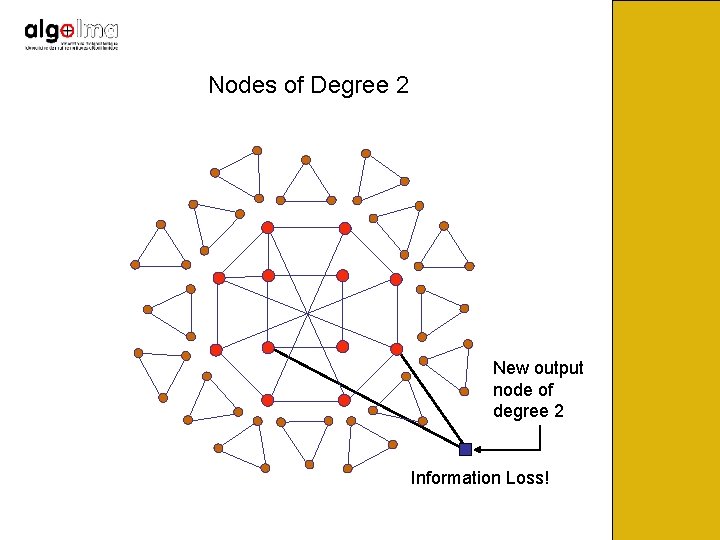
Nodes of Degree 2

Nodes of Degree 2 New output node of degree 2 Information Loss!

Fraction of Nodes of Degree 2 If there exists component of linear size (i. e. , a giant component), then next output node of degree 2 has constant probability of being useless. Therefore, graph should not have giant component. This means that for capacity achieving degree distributions we must have: On the other hand, if successfully. So, then algorithm cannot start for capacity-achieving codes:

The -ary symmetric channel (large ) Double verification decoding (Luby-Mitzenmacher): If and are correct, then they verify. Remove all of them from graph and continue. Can be shown that number of correct output symbols needs to be at least Times number of input symbols.

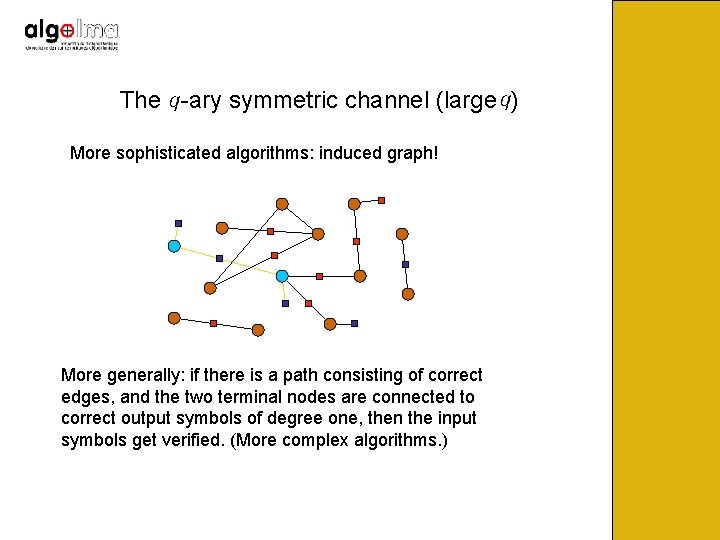
The -ary symmetric channel (large ) More sophisticated algorithms: induced graph! If two input symbols are connected by a correct output symbol, and each of them is connected to a correct output symbol of degree one, then the input symbols are verified. Remove from them from graph.

The -ary symmetric channel (large ) More sophisticated algorithms: induced graph! More generally: if there is a path consisting of correct edges, and the two terminal nodes are connected to correct output symbols of degree one, then the input symbols get verified. (More complex algorithms. )

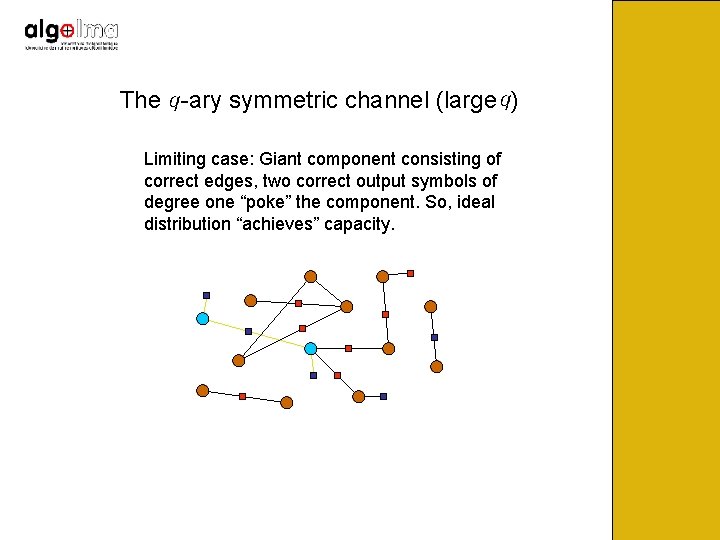
The -ary symmetric channel (large ) Limiting case: Giant component consisting of correct edges, two correct output symbols of degree one “poke” the component. So, ideal distribution “achieves” capacity.

Binary Memoryless Symmetric Channels What is the fraction of nodes of degree 2 for capacityachieving Raptor Codes? where, in general and is the LLR of the channel.

General Symmetric Channels: Mimic Proof is information theoretic: if fraction of nodes of degree 2 is larger by a constant, then : • Expectation of the hyperbolic tangent of messages passed from input to output symbols at given round of BP is larger than a constant. • This shows that • So code cannot achieve capacity.

General Symmetric Channels: Mimic Proof Fraction of nodes of degree one for capacity-achieving Raptor Codes: Noisy observations of Therefore, if , and if of degree one, then So denote output nodes

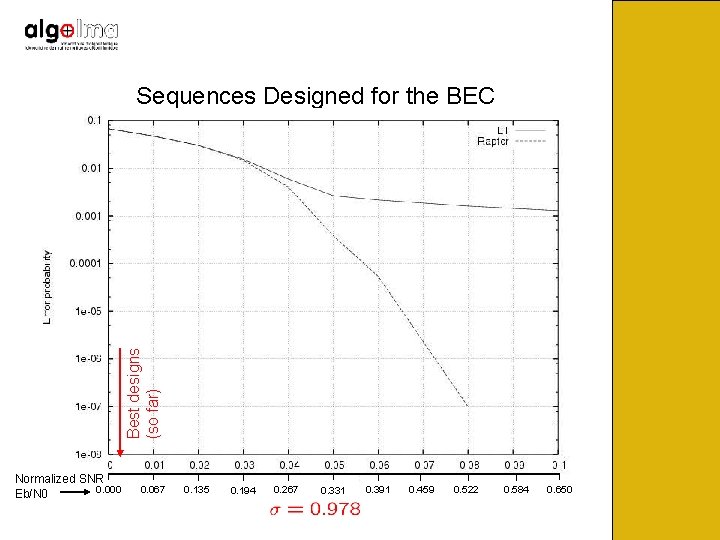
Best designs (so far) Sequences Designed for the BEC Normalized SNR 0. 000 Eb/N 0 0. 067 0. 135 0. 194 0. 267 0. 331 0. 391 0. 459 0. 522 0. 584 0. 650

Conclusions • For LT- and Raptor codes, some decoding algorithms can be phrased directly in terms of subgraphs of graphs induced by output symbols of degree 2. • This leads to a simpler analysis without the use the tree assumption. • For the BEC, and for the q-ary symmetric channel (large q) we obtain essentially the same limiting capacityachieving degree distribution, using the giant component analysis. • An information theoretic analysis gives the optimal fraction of output nodes of degree 2 for general memoryless symmetric channels. • A graph analysis reveals very good degree distributions, which perform very well experimentally.