This class l Applications of network flow Maximum

This class l Applications of network flow

Maximum Bipartite Matching Given an undirected graph G = (V, E) l A matching is a subset of edges M E such that for all v V, at most one edge of M is incident on v. l A maximum matching is a matching of maximum cardinality l

Maximum Bipartite Matching (cont. ) l Assume that G is bipartite – The vertex set V = L R – L and R are disjoint – All undirected edges in E are between L and R l Assume further that every vertex in V has at least one incident edge.

The Network for Maximum Bipartite Matching l The flow network G’ = (V’, E’) for the bipartite graph is: – V’ = V {s, t} where the source s and sink t are new vertices and – E’ = {(s, u) | u L} {(u, v) | u L, v R and (u, v) E} {(v, t) | v R} – c(e) = 1 for each e E’

The Network (continued) |E’| = |L| + |R| + |E| = |V| + |E| l Since |E| |V/2|, |E’| 3|E| l Since f*=|M| min{|L|, |R|} = O(V) Ford and Fulkerson finds a maximum flow in G’ in O(VE’) = O(VE) l

Lemma 26. 10 l l G = (V, E) is a bipartite graph with V = L R. G’ = (V’, E’) is a corresponding flow network. a) If M is a matching in G, there is an integer-valued flow f in G’ with value |f| = |M|. b) If f is an integer valued flow in G’, there is a matching M in G, with |M| = |f|

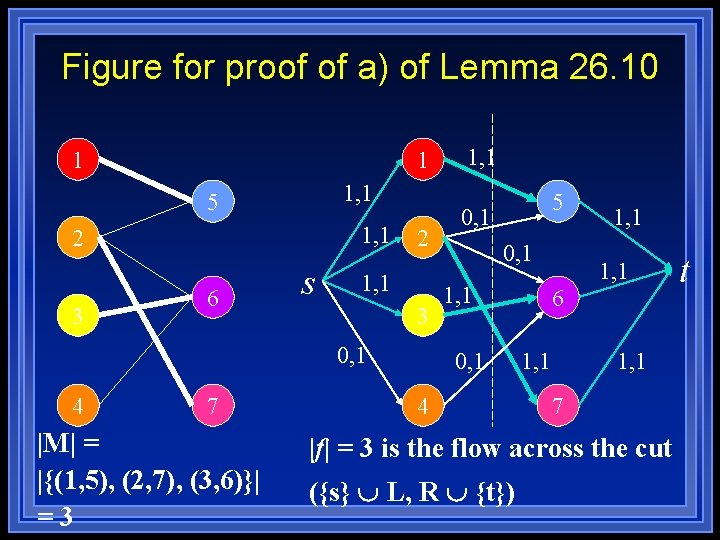
Proof of a) l Given a matching M. The flow corresponding to M: – For every (u, v) M, f(s, u) = f(u, v) = f(v, t) = 1 and f(u, s) = f(v, u) = f(t, v) = -1 – f(u, v) = 0 for all other edges (u, v) E’ l l It is easy to see that f is a flow (satisfies, skew symmetry, capacity constraint and flow conservation) The net flow across the cut (L {s}, R {t}) is equal to |f| = |M|

Figure for proof of a) of Lemma 26. 10 1 1 1, 1 5 1, 1 2 3 6 s 2 1, 1 3 0, 1 4 7 |M| = |{(1, 5), (2, 7), (3, 6)}| =3 1, 1 5 0, 1 1, 1 0, 1 4 1, 1 6 1, 1 7 |f| = 3 is the flow across the cut ({s} L, R {t}) t

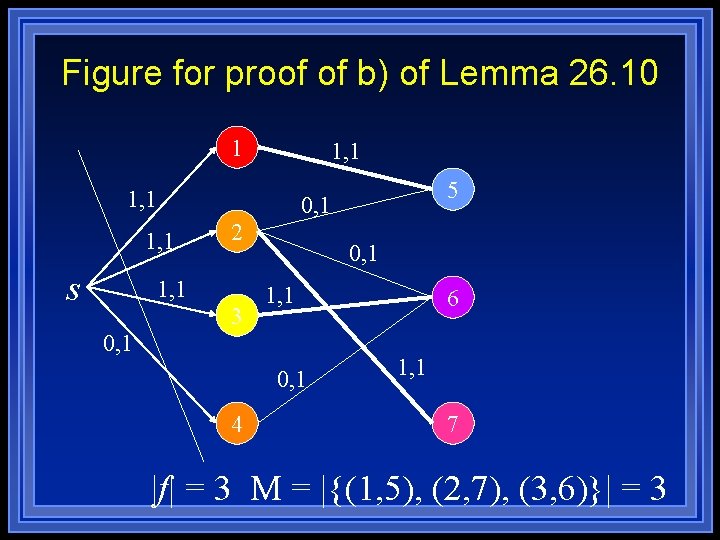
Proof of b) l l l Given an integer valued flow f in G’ Let M = {(u, v) | u L, v R and f(u, v) > 0} M is a matching since every vertex v in G is incident on at most one edge in M – Only 1 unit of flow can enter and thus leave v L – Only 1 unit of flow can leave and thus enter v R l |M| = |f| since for each u L and u is matched we have f(s, u) = 1, and for every u L and u is not matched f(s, u) = 0

Figure for proof of b) of Lemma 26. 10 1 1, 1 0, 1 1, 1 s 5 2 1, 1 3 0, 1 1, 1 0, 1 4 6 1, 1 7 |f| = 3 M = |{(1, 5), (2, 7), (3, 6)}| = 3

Theorem 26. 11 l If all the capacities in a flow network are integer: a) The maximum flow |f| produced by Ford and Fulkerson is integer b) For all pairs of vertices u, and v, f(u, v) is an integer

Corollary 26. 12 The cardinality of a maximum matching M in a bipartite graph G equals the value of a maximum flow f in its corresponding flow network G’

Supply and Demand Networks l There is a function d(v) associated with each vertex v, – d(v) > 0 indicates demand – d(v) < 0 indicates supply – d(v)=0 indicates transshipment l The sum of all the demands = D sum of supplies

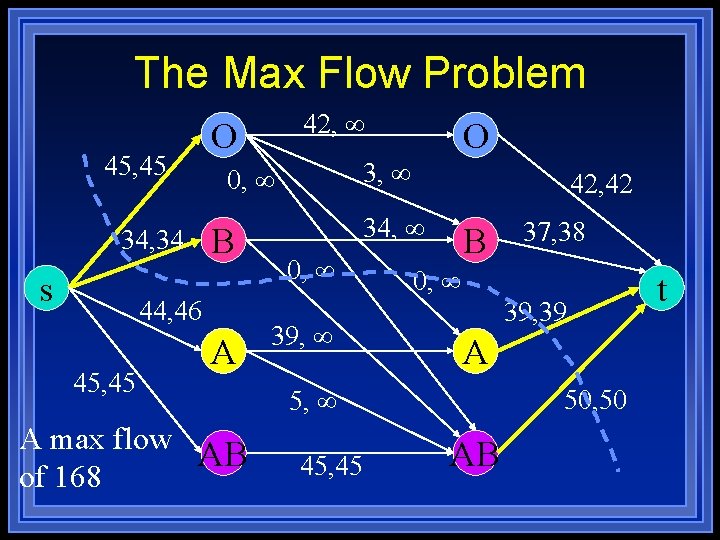
Supply and Demand (continued) l Max flow formulation – Add source s and sink t – For each supply at v (d(v) < 0) add edge (s, v) with c(s, v) = -d(v) – For each demand at v (d(v) > 0) add edge (v, t) with capacity c(v, t) = d(v). l Problem has a solution if |f| = D

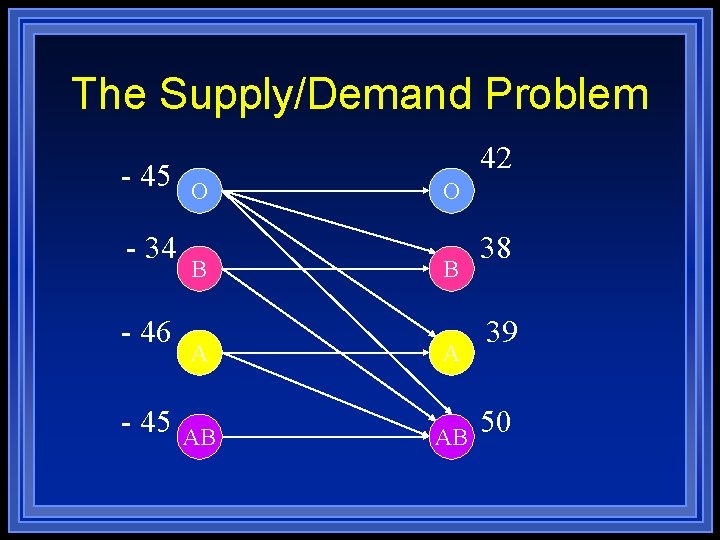
Blood Transfusion Example Because of a bio-terrorism attack, hospital L has 169 patients who need a blood transfusion l The hospital has supplies of 170 units of blood l Blood Type A B O AB Supply 46 34 45 45 Demand 39 38 42 50

Example Continued l l l Type A patients can only receive type A or O Type B patients can only receive type B or O Type O patients can only receive type O Type AB patients can receive A, B, O or AB Can the hospital satisfy the demand?

The Supply/Demand Problem - 45 - 34 - 46 - 45 42 O B A AB 38 39 50

The Max Flow Problem 45, 45 34, 34 s B A A max flow AB of 168 O 3, 0, 44, 46 45, 45 42, O 42, 42 34, 0, 39, B 0, 39, 39 A 5, 45, 45 37, 38 50, 50 AB t

The baseball elimination problem l l l Assume n+1 teams You want to know if the Red Sox (RX) still have a chance of winning the league. Let w 0 denote the number of wins of team 0 = RX wmax the total number of wins that RX can have if it wins the rest of its games. Consider the rest of the teams 1, …, n. Assume that pairs of teams (i, j) have g(i, j) games to play. RX cannot be eliminated if after the rest of the games of teams 1, …, n are played it is possible that no team has more wins than wmax

The network problem l l l Let nodes 1, …, n denote teams 1, …, n Let node (i, j) denote a game between teams i and j where i < j. Add an edge from node i for i = 1, …, n, to all the nodes (k, l) such that i = k or i = l. Give all the edges an infinite capacity. The “supply” at each node i is wmax – wi where wi is the number of wins so far of team i The “supply” is the maximum number of additional wins that team i can have before team 0 can be eliminated

The network problem l l The “demand” at each pair (i, j) is the number of remaining games g(i, j) teams i and j must play. If all the “demands” can be satisfied team 0 cannot be eliminated

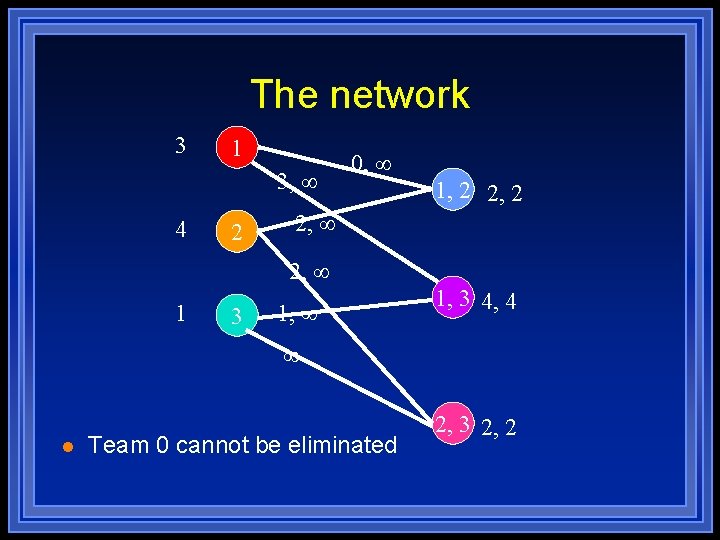
Example 1 l l l Assume teams 0, 1, 2, 3. Team 0 won 19 games and has 2 more games with 1 and 3 more games with 2. wmax = 24. Team 1 won 21 games and has 2 more games with 2 and 4 more games with 3. “Supply” of 1 =24 – 21=3 Team 2 won 20 games and has 2 more games with 3. “Supply” of 2 =4. Team 3 won 23 games. “Supply” of 3 = 1

The network 3 1 3, 4 2 0, 1, 2 2, 2, 1 3 1, 1, 3 4, 4 l Team 0 cannot be eliminated 2, 3 2, 2

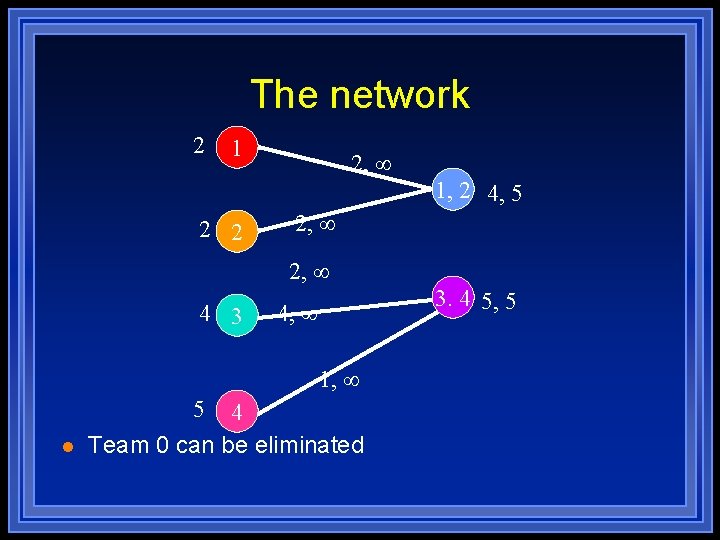
Example 2 l l l l Assume teams 0, 1, 2, 3, 4. Team 0 won 19 games and has 2 more games with 1 and 3 more games with 2. wmax = 24. Team 1 won 22 games “Supply” of 1 =2 Team 2 won 22 games. “Supply” of 2 =2. Team 3 won 20 games. “Supply” of 3 = 4 Team 4 won 19 games. “Supply” of 4 = 5 Team 1 has 5 more games with 2. Team 3 has 5 more games with 4

The network 2 1 2, 1, 2 4, 5 2 2 2, 4 3 3. 4 5, 5 4, 1, 5 l 4 Team 0 can be eliminated

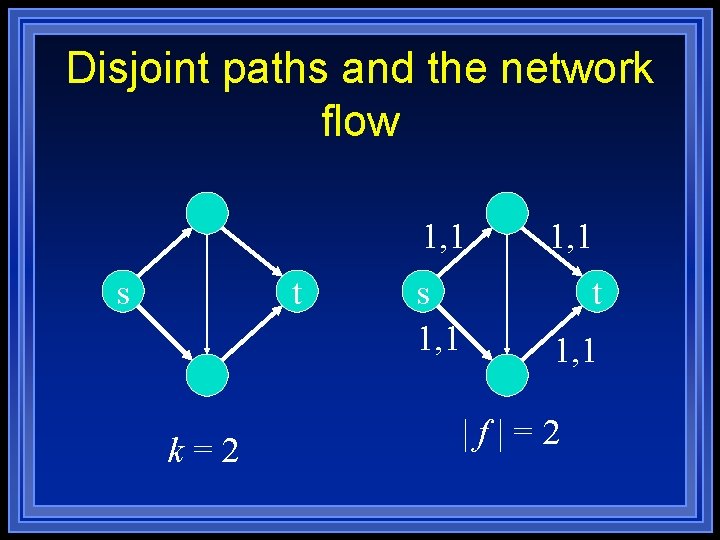
Disjoint Paths l l Two paths are edge-disjoint if they have no edge in common. Disjoint path problem: find max number of edge-disjoint s-t paths in a directed graph with source s and sink t Application: communication networks Max flow formulation: assign unit capacity to every edge.

Disjoint paths and the network flow s t k=2 1, 1 s 1, 1 t 1, 1 |f|=2

Theorem l Given a directed graph with a single source s and a single sink t, it has k edge-disjoint paths from s to t if and only if max flow value is k

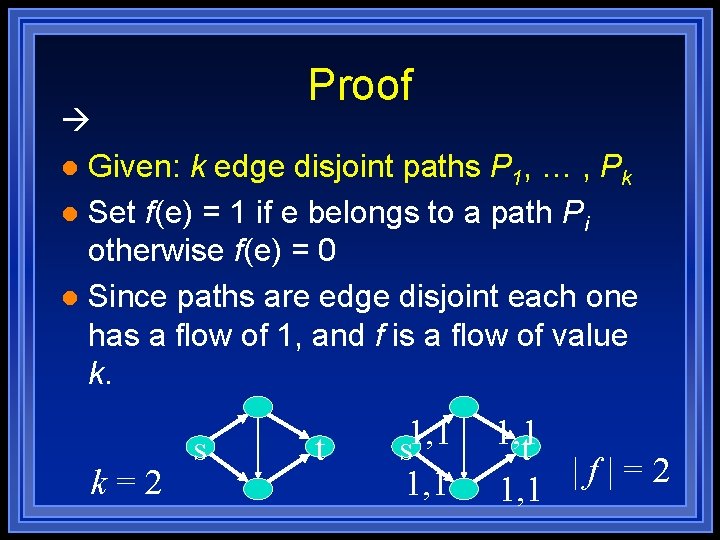
Proof l Given: k edge disjoint paths P 1, … , Pk l Set f(e) = 1 if e belongs to a path Pi otherwise f(e) = 0 l Since paths are edge disjoint each one has a flow of 1, and f is a flow of value k. k=2 s t 1, 1 s 1, 1 t |f|=2 1, 1

Proof l Given: max flow value is k l There exists an integer flow, where all f(e) are 0 or 1 l Consider an edge (s, v) with f(s, v) = 1 – By conservation there exists an edge (v, w) with f(v, w) = 1 – Continue choosing edges until t is reached l Process finds k edge-disjoint paths

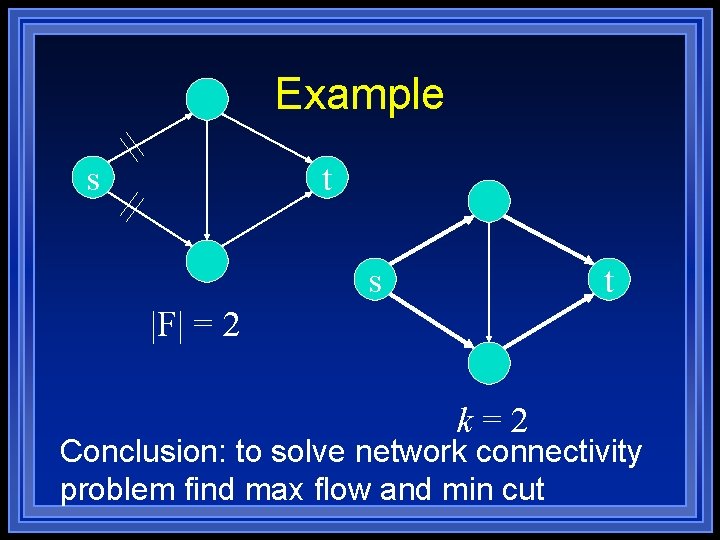
Network Connectivity l l l Given a directed graph with one source s and one sink t. A set of edges F E is called an (s, t) edge separator if every path from s to t passes through at least one edge of T. Let M(s, t) be the smallest cardinality of an (s, t) edge separator. s-t network connectivity: compute M(s, t). Network connectivity: compute

Menger’s Theorem (1926) l l l The max number of edge disjoint s-t paths p(s, t)= min number of edges whose removal disconnects t from s M(s, t). Proof Let the number of edge disjoint paths be k and Let the set of edges whose removal disconnects t from s be F We need to show |F|=k

Menger’s Theorem Proof cont. l Since max number of edge-disjoint paths is k, the corresponding max flow is also k l So there is a min-cut (S, T) of capacity k l Let F’ be the set of edges going from S to T l Each has a flow and capacity of 1, so |F|’ = k and F’ disconnects t from s l Since F is a minimal disconnecting subset |F|<=|F’|=k

Menger’s Theorem Proof cont. l Suppose the removal of the edges in F disconnects t from s, and F is minimal. l Since F disconnects s from t each disjoint s-t path uses at least one edge of F l Hence the number of edge disjoint paths k<= |F| l So |F|=k

Example s t |F| = 2 k=2 Conclusion: to solve network connectivity problem find max flow and min cut