Maximum Flow n Maximum Flow A flow network

Maximum Flow

n Maximum Flow A flow network G=(V, E) is a DIRECTED graph where each has a nonnegative capacity u p 2.

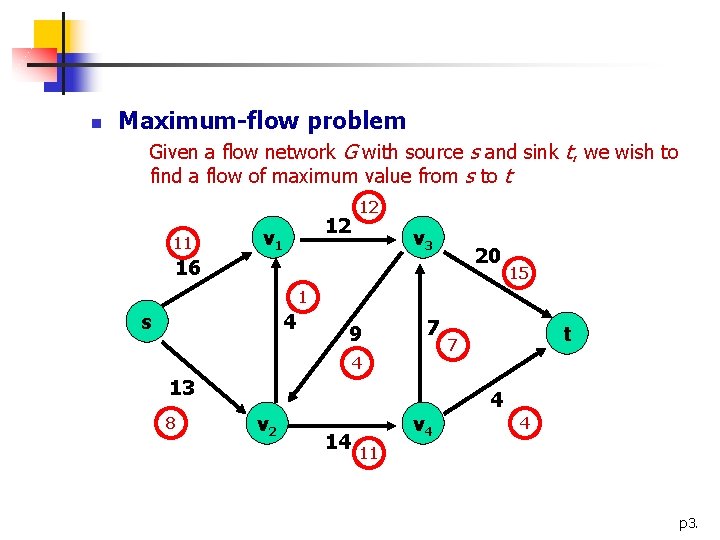
n Maximum-flow problem Given a flow network G with source s and sink t, we wish to find a flow of maximum value from s to t 11 12 v 3 20 16 15 1 s 4 9 7 4 13 8 v 2 14 v 4 t 7 4 4 11 p 3.

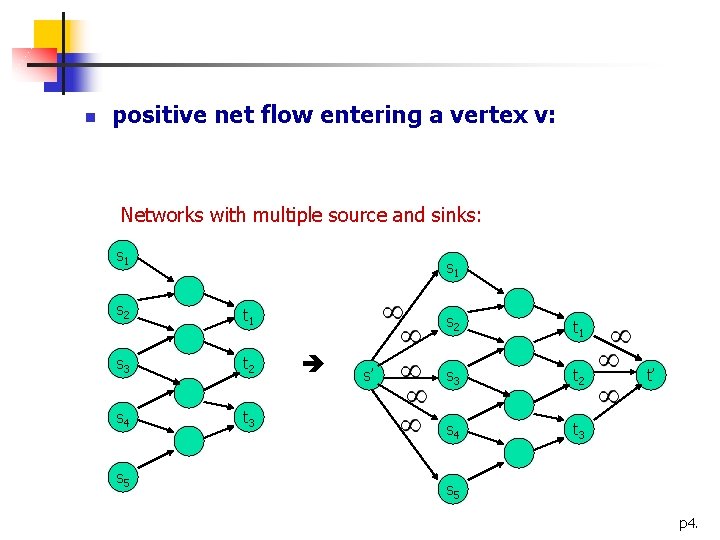
n positive net flow entering a vertex v: Networks with multiple source and sinks: s 1 s 2 t 1 s 3 t 2 s 4 t 3 s 5 s’ s 2 t 1 s 3 t 2 s 4 t 3 t’ s 5 p 4.

n Ford-Fulkerson method n Residual networks p 5.

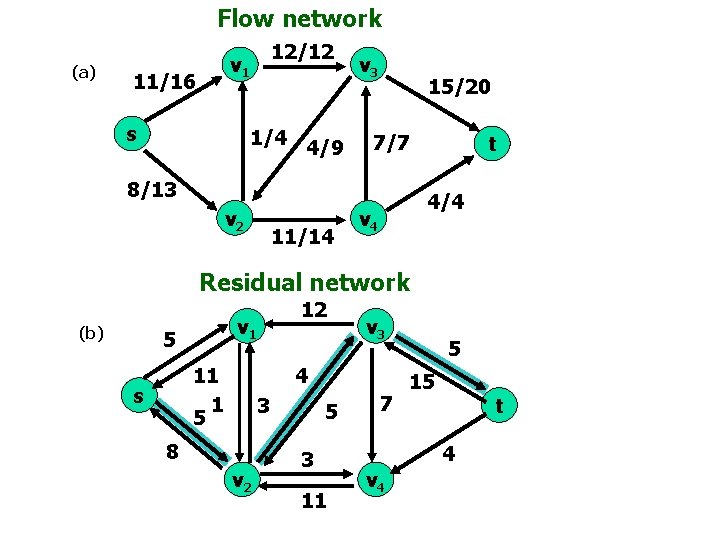
Flow network (a) 12/12 v 1 11/16 s 1/4 4/9 v 3 15/20 7/7 8/13 v 2 11/14 t 4/4 v 4 Residual network (b) v 1 5 11 1 5 s 12 v 3 4 3 8 v 2 5 3 11 7 5 15 t 4 v 4

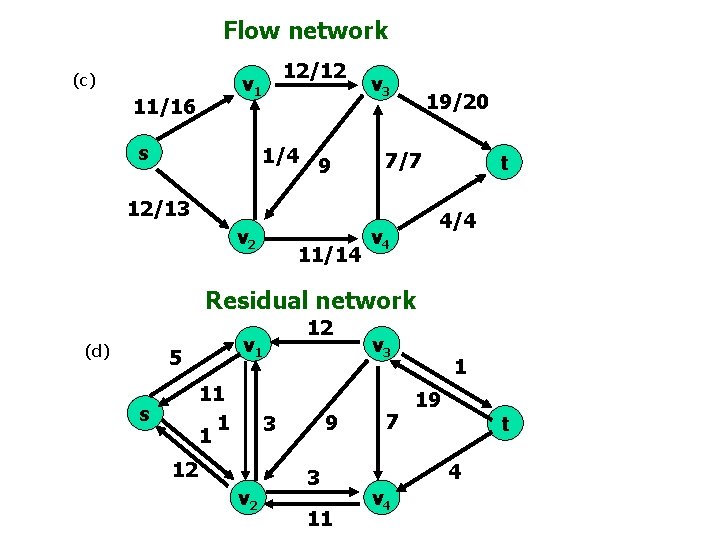
Flow network (c) 12/12 v 1 11/16 s 1/4 9 v 3 19/20 7/7 12/13 v 2 11/14 t 4/4 v 4 Residual network (d) v 1 5 11 1 1 s 12 9 3 12 v 2 3 11 v 3 7 1 19 t 4 v 4

n Lemma 1 Pf: p 8.

p 9.

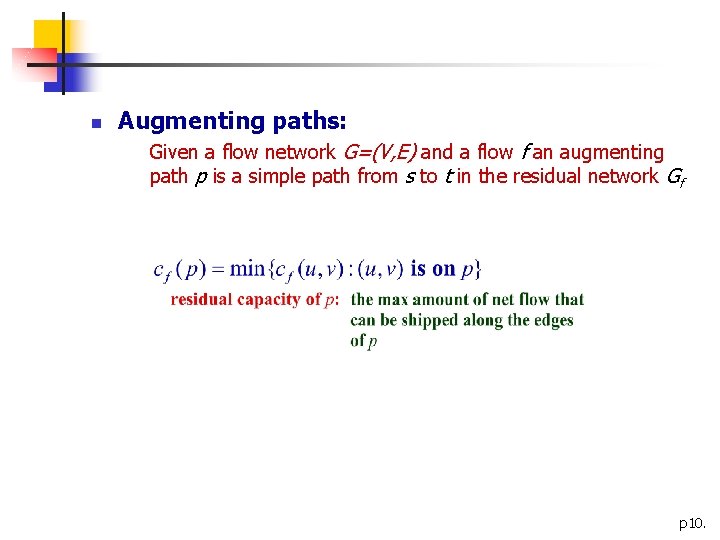
n Augmenting paths: Given a flow network G=(V, E) and a flow f an augmenting path p is a simple path from s to t in the residual network Gf p 10.

n Lemma 2: n Corollary 3: p 11.

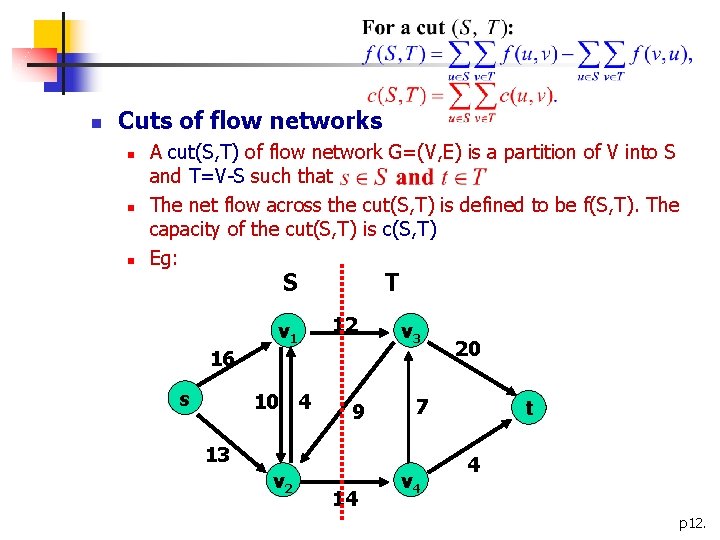
n Cuts of flow networks n n n A cut(S, T) of flow network G=(V, E) is a partition of V into S and T=V-S such that The net flow across the cut(S, T) is defined to be f(S, T). The capacity of the cut(S, T) is c(S, T) Eg: S 16 s v 1 10 4 T 12 9 v 3 7 13 v 2 14 20 v 4 t 4 p 12.

n Lemma 4 Pf: p 13.

n Cor 5 Pf: p 14.

n Thm 6 (Max-flow min-cut theorem) Pf: p 15.

p 16.

n The basic Ford-Fulkerson algorithm M M s t 1 M M p 17.

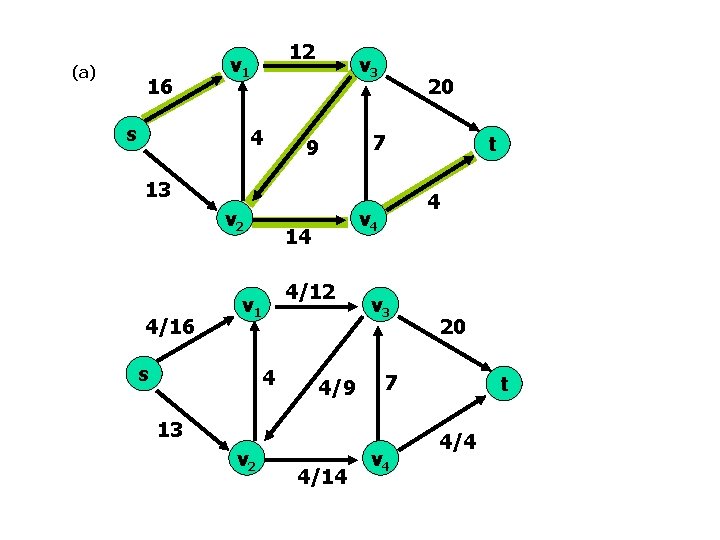
(a) 16 12 v 1 s 4 v 3 9 20 7 13 v 2 4/16 v 1 s 4 4 v 4 14 4/12 4/9 v 3 4/14 20 7 13 v 2 t v 4 t 4/4

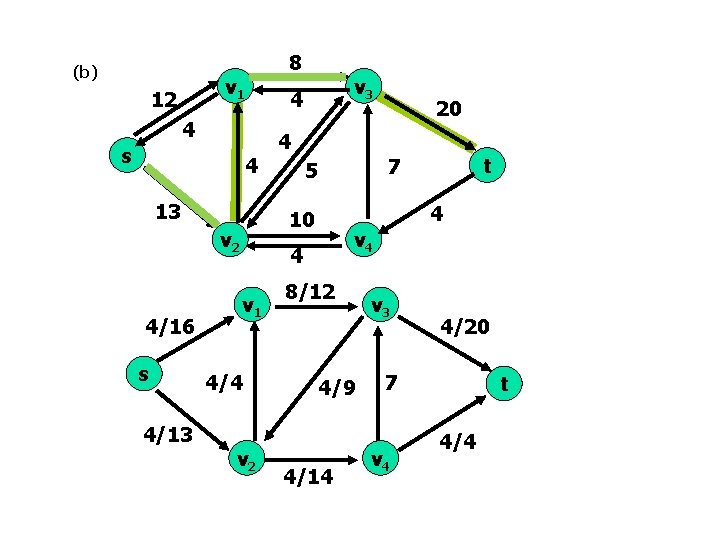
(b) v 1 12 4 s 4 13 s 4/13 v 3 4 4/4 v 2 t 7 5 4 v 4 4 v 1 20 4 10 v 2 4/16 8 8/12 4/9 4/14 v 3 4/20 7 v 4 t 4/4

(c) v 1 12 4 s 9 4 8/12 9 v 3 4/14 8/20 7 4/13 v 2 t v 4 4 v 1 4 4 10 v 2 16 7 5 4 s v 3 8 4 4 8/16 4 v 4 t 4/4

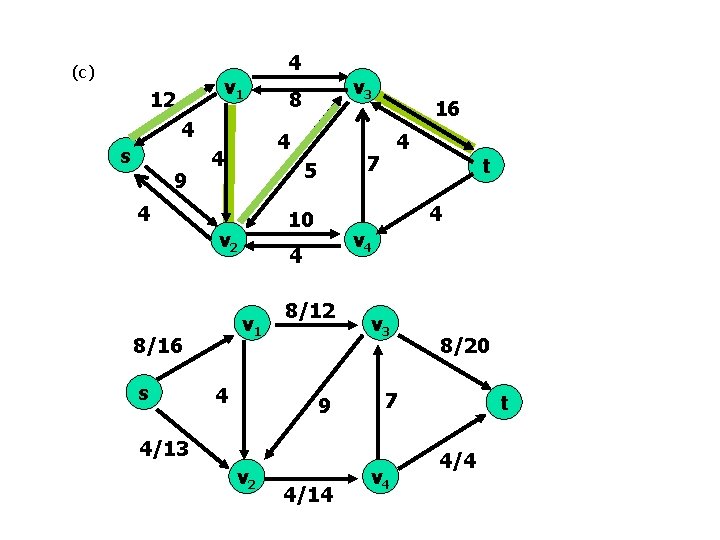
(d) 4 v 1 8 8 8 s 9 4 s 4 8/12 9 v 3 11/14 15/20 7/7 11/13 v 2 t v 4 4 v 1 8 4 10 v 2 12 7 9 4 8/16 v 3 v 4 t 4/4

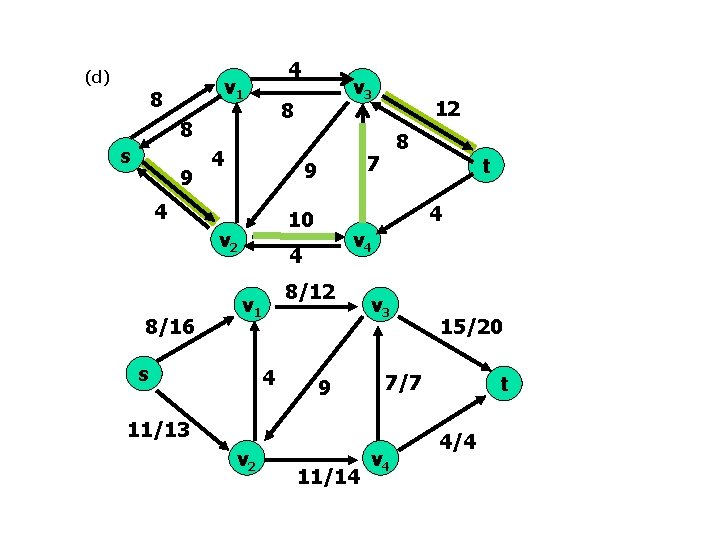
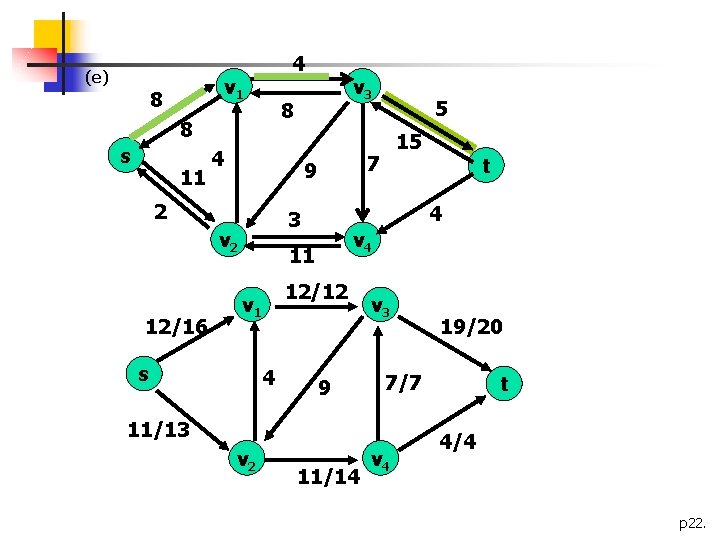
(e) 4 v 1 8 8 8 s 11 4 s 4 12/12 9 v 3 11/14 19/20 7/7 11/13 v 2 t v 4 11 v 1 15 4 3 v 2 5 7 9 2 12/16 v 3 v 4 t 4/4 p 22.

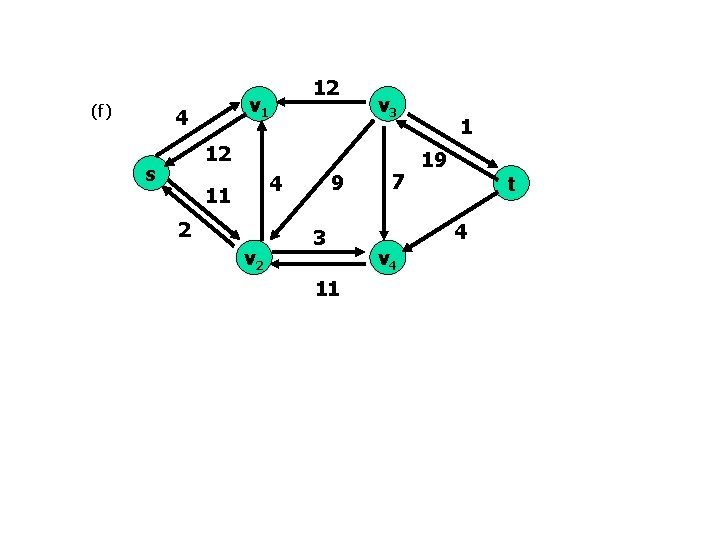
(f) v 1 4 12 v 3 12 s 9 4 11 2 v 2 3 11 7 1 19 t 4 v 4

n Edmonds-Karp algorithm n Implement the computation of the augmenting path p with a breadth-first search. n That is the augmenting path is a shortest path from s to t in the residual network, where each edge has unit distance. p 24.

n Lemma 7 Pf: (*) p 25.

p 26.

n Thm 8 Pf: p 27.

p 28.

There at most O(E) pairs of vertices that can have an edge between them in a residual graph, the total number of critical edges during the entire execution of the Edmonds-Karp algorithm is O(VE). Each augmenting path has at least one critical edge, and hence theorem follows. Each iteration of Ford-Fulkerson can be implemented in O(E) time, when the augmenting path is found by BFS. Total running time of the Edmonds-Karp algorithm is O(VE 2). Asymptotically fastest to date for maximum-flow：