The Power of Negations in Cryptography Siyao Guo

The Power of Negations in Cryptography Siyao Guo Tal Malkin Igor C. Oliveira Alon Rosen New York University Columbia University IDC Herzilya

How simple can cryptography be? • Cryptography in restricted/simple models • constant depth circuits [AIK 06] • linear size circuits [IKOS 08] • Philosophy behind this line of research Positive results: extreme efficiency (cryptography) • Negative results: lower bounds for the model (complexity) • Simple models: fun to play (me) •

Monotone Cryptography? [GI 12] • [GI 12] Can OWFs and PRGs be computable by monotone circuits? Normal circuits: {AND, OR, NOT} OWFs, PRGs (assume OWFs exit) Monotone circuits: {AND, OR, NOT} OWFs, PRGs • (assume OWFs exit) “Monotone world”: a fundamental gap between OWFs and PRGs; “hardness-vs-pseudorandomness” paradigm fails

Our Question • [GI 12] Can OWFs and PRGs be computable by monotone circuits? • How about other primitives? • How about circuits with few negations? 4

The Mystery of Negations • [Juk 12] The main difficulty in proving nontrivial lower bounds on the size of circuits using AND, OR and NOT is the presence of NOT gates—we already know how to prove even exponential lower bounds for monotone functions if no NOT gates are allowed. The effect of such gates on circuit size remains to a large extent a mystery. • [Mark 58] Any Boolean function can be computed by a Boolean circuit with at most log(n)+1 negations.

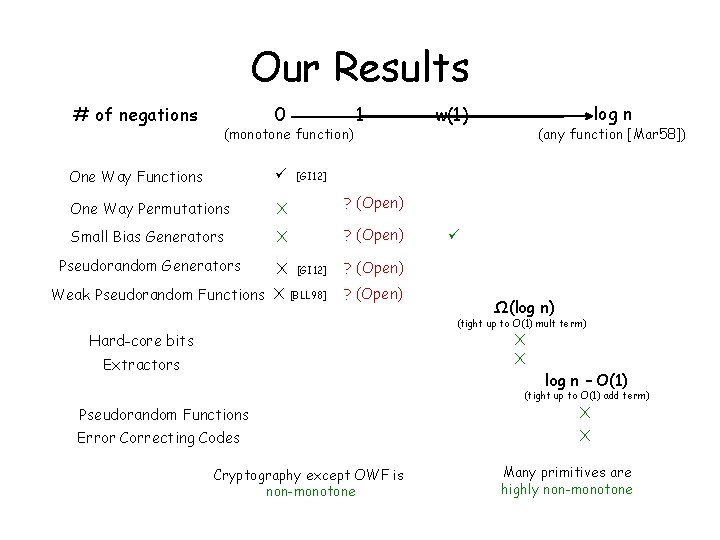
Our Results # of negations 0 (monotone function) 1 One Way Functions One Way Permutations X ? (Open) Small Bias Generators X ? (Open) Pseudorandom Generators X log n w(1) (any function [Mar 58]) [GI 12] ? (Open) Weak Pseudorandom Functions X [BLL 98] ? (Open) Ω(log n) (tight up to O(1) mult term) X X Hard-core bits Extractors log n – O(1) (tight up to O(1) add term) Pseudorandom Functions X Error Correcting Codes X Cryptography except OWF is non-monotone Many primitives are highly non-monotone

CRYPTOGRAPHY (OWF V. S OWP) IS NON-MONOTONE

Monotone OWFs [GI 12] • [GI 12] OWFs exist => monotone OWFs exist - Middle slice of any OWF is a monotone weak OWF - (Standard) Monotone weak OWF => monotone OWF • Middle slice of OWF f: {0, 1}n->{0, 1}n is defined as f’(x) = 1 n if |x| > n/2 f’(x) = f(x) if |x| = n/2 f’(x) = 0 n if |x| < n/2 [GI 12] size(C(f’)) = poly(n) size(C(f)) • Can we show OWPs exist => monotone OWPs exist? - This transformation doesn’t preserve the structure

X Monotone OWPs • Thm 1: If f: {0, 1}n -> {0, 1}n is a monotone permutation, then a permutation π: [n] -> [n], s. t. f(x 1, … , xn)= xπ(1) , … , xπ(n). • An efficient inverting algorithm for y = f(x): • • • Compute π’ = π-1: for i in [n], if f(ei) = ej , then set π’(j)=i (ei = 0 i-110 n-i) Given y 1, . . , yn, output yπ’(1), …, yπ’(n) Two Proofs for Theorem 1 • • Combinatorial proof : only relies on monotonicity Analytic proof: simple and easy to extend to regular OWFs

A Powerful Tool For monotone functions f, g: {0, 1}n -> {0, 1} • FKG’s inequality: (monotone functions are positively correlated) • Talagrand’s inequality: (the correlation can be lower bounded) where (C > 0 is a fixed constant)

Proof of Theorem 1 • For any two output functions fj , fk by Talagrand’s inequality = 1/4 = 1/2 => =0 fj, fk depend on disjoint input coordinates • f 1, . . . , fn depend on disjoint coordinates • • Each one depends on and equals to exactly 1 input coordinate f is a permutation of input coordinates

MANY PRIMITIVES MONOTONE ARE HIGHLY NON-

Tool Box • Talagrand’s inequality fails for 1 negation • Structure results for function with negations Markov ‘s theorem • Decomposition theorem • Selection tree •

Tool 1: Markov’s Theorem • Chain X: (x 1, …, xl) where xi <= xi+1 x 1 , … , xl f(x 1) , … , f(xl) • a(f, X): alternating number of X respect to f number of values flipping along the chain • [Mar 58] f with t negations => max. X a(f, X) = O(2 t)

Pseudorandom Functions (PRFs) • Thm 3: If F {0, 1}s x {0, 1}n -> {0, 1} is (poly(n), 1/3)-secure PRFs, then F requires logn –O(1) negations. • Distinguishier: fixed an arbitrary chain, e. g. X= (x 0, x 1, …, xn) where xi = 1 i 0 n-i if a(f, X) >= n/4, outputs 1 otherwise 0. • Analysis: Random functions: E[a(f, X)] = n/2 a(f, X)>= n/4 w. h. p F with t = logn – ω(1): a(f, X) < O(2 t) = o(n).

Tool 2: Decomposition • [BCO+14] If f can be computable by t negations, then f(x) = h(g 1(x), … , g. T(x)) where gi is monotone, T = O(2 t), h is XOR or its negation. • A bound on total influence I(f) • Large influence requires many negations

Applications in Cryptography • Lower bounds for primitives requiring large influences • • [GR 00] Hardcore bits require large influence [BG 13] Extractors require large influence Extractors and hardcore bits require Ω(log n) negations More application? Checking results use influence as a “black box” • • Monotone setting Low depth circuits setting

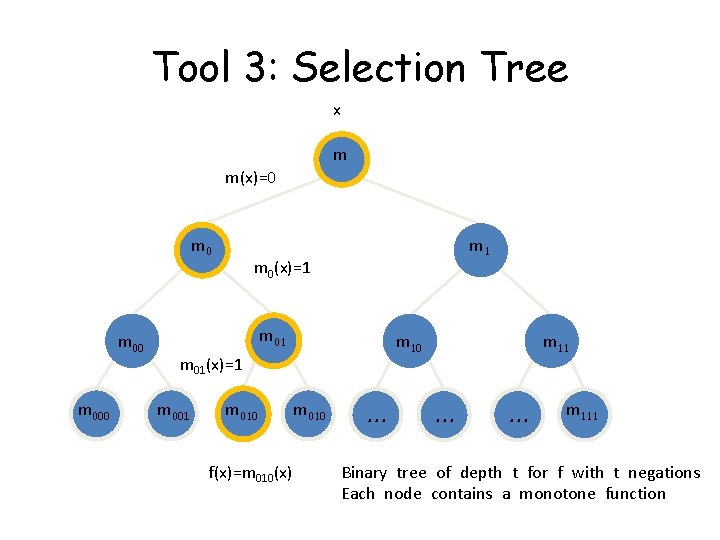
Tool 3: Selection Tree x m m(x)=0 m 000 m 1 m 0(x)=1 m 01 m 10 m 01(x)=1 m 001 m 010 f(x)=m 010(x) m 010 … m 11 … … m 111 Binary tree of depth t for f with t negations Each node contains a monotone function

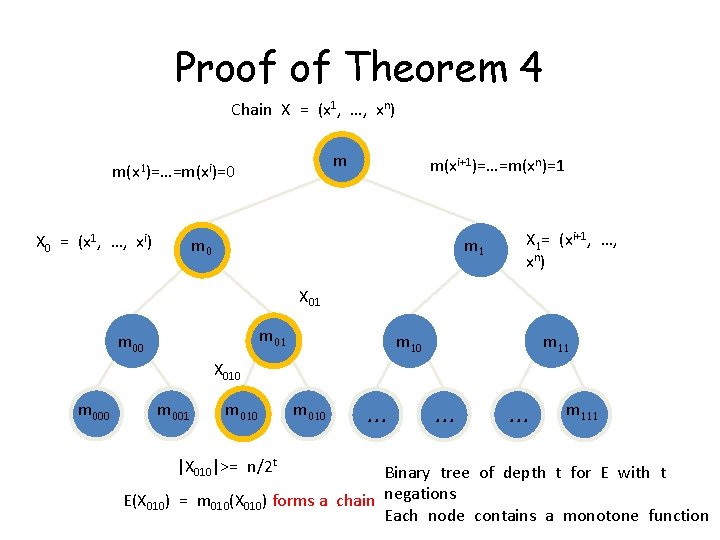
Error-Correcting Codes (ECCs) • [BKS 06]: If E: {0, 1}n -> {0, 1}m is a monotone ECC, then E has relative distance r <= 1/n. • Thm 4: If E: {0, 1}n -> {0, 1}m is an ECC with relative distance r, then E requires t negations, t>= logn – log(1/r), i. e. , r <= 2 t/n • ECC with r=O(1) requires logn – O(1) negations (optimal up to additive term)

Proof Idea of [BKS 06] • Consider a (monotone) chain and the encoding • E is monotone implies E(X) forms a (monotone) chain • |X| = n+1 thus r <= 1/n

Proof of Theorem 4 Chain X = (x 1, …, xn) m m(x 1)=…=m(xi)=0 X 0 = (x 1, …, xi) m(xi+1)=…=m(xn)=1 m 0 m 1 X 1= (xi+1, …, xn ) X 01 m 00 m 11 X 010 m 001 m 010 |X 010|>= n/2 t m 010 … … … m 111 Binary tree of depth t for E with t E(X 010) = m 010(X 010) forms a chain negations Each node contains a monotone function

Summary • Cryptography is non-monotone except OWF Talangrand’s inequality • OWPs, SBGs, PRGs, (weak) PRFs • • Many primitives are highly non-monotone Alternating • Xor of monotones (low influence) • Selection • - PRFs - HCBs, EXTs - ECCs

Open Problems • Negation complexity of OWPs, PRGs • • • Negation complexity of weak PRFs • • Is there a OWP/PRG computable by 1 negation? 1 negation at the bottom cannot compute OWPs/PRGs Is there a weak PRF computable by 1 negation? PRFs: require logn –O(1) negations at the bottom cannot compute weak PRFs Negation complexity of parallel cryptography • • • Markov’s theorem fails for constant depth circuits AC 0 Prove Ω(n) lower bounds for primitives in AC 0? Explain why we need many negations in efficient construction

THANKS