Testing a Claim Testing a Claim n Significance


















































- Slides: 62

+ Testing a Claim

+ Testing a Claim n Significance Tests: The Basics n Tests about a Population Proportion n Tests about a Population Mean

+ Significance Tests: The Basics Learning Objectives After this section, you should be able to… ü STATE correct hypotheses for a significance test about a population proportion or mean. ü INTERPRET P-values in context. ü INTERPRET a Type I error and a Type II error in context, and give the consequences of each. ü DESCRIBE the relationship between the significance level of a test, P(Type II error), and power.

A significance test is a formal procedure for comparing observed data with a claim (also called a hypothesis) whose truth we want to assess. The claim is a statement about a parameter, like the population proportion p or the population mean µ. We express the results of a significance test in terms of a probability that measures how well the data and the claim agree. In this chapter, we’ll learn the underlying logic of statistical tests, how to perform tests about population proportions and population means, and how tests are connected to confidence intervals. Significance Tests: The Basics Confidence intervals are one of the two most common types of statistical inference. Use a confidence interval when your goal is to estimate a population parameter. The second common type of inference, called significance tests, has a different goal: to assess the evidence provided by data about some claim concerning a population. + n Introduction

Reasoning of Significance Tests We can use software to simulate 400 sets of 50 shots assuming that the player is really an 80% shooter. You can say how strong the evidence against the player’s claim is by giving the probability that he would make as few as 32 out of 50 free throws if he really makes 80% in the long run. The observed statistic is so unlikely if the actual parameter value is p = 0. 80 that it gives convincing evidence that the player’s claim is not true. Significance Tests: The Basics Statistical deal with claims abouttoa be population. Tests ask shooter. if sample Suppose atests basketball player claimed an 80% free-throw good evidence against a claim. A test might He say, makes “If we 32 took Todata test give this claim, we have him attempt 50 free-throws. of many. His random samples andof the claimshots wereistrue, we=would them. sample proportion made 32/50 0. 64. rarely get a result like this. ” To get a numerical measure of how strong the sample What can we about the term claim“rarely” based on sample data? evidence is, conclude replace the vague by this a probability. + n The

Reasoning of Significance Tests In reality, there are two possible explanations for the fact that he made only 64% of his free throws. 1) The player’s claim is correct (p = 0. 8), and by bad luck, a very unlikely outcome occurred. 2) The population proportion is actually less than 0. 8, so the sample result is not an unlikely outcome. Basic Idea An outcome that would rarely happen if a claim were true is good evidence that the claim is not true. Significance Tests: The Basics Based on the evidence, we might conclude the player’s claim is incorrect. + n The

Hypotheses Definition: The claim tested by a statistical test is called the null hypothesis (H 0). The test is designed to assess the strength of the evidence against the null hypothesis. Often the null hypothesis is a statement of “no difference. ” The claim about the population that we are trying to find evidence for is the alternative hypothesis (Ha). In the free-throw shooter example, our hypotheses are H 0 : p = 0. 80 Ha : p < 0. 80 where p is the long-run proportion of made free throws. Significance Tests: The Basics A significance test starts with a careful statement of the claims we want to compare. The first claim is called the null hypothesis. Usually, the null hypothesis is a statement of “no difference. ” The claim we hope or suspect to be true instead of the null hypothesis is called the alternative hypothesis. + n Stating

Hypotheses The alternative hypothesis has one of the forms Ha : parameter < value Ha : parameter > value Ha : parameter ≠ value To determine the correct form of Ha, read the problem carefully. Definition: The alternative hypothesis is one-sided if it states that a parameter is larger than the null hypothesis value or if it states that the parameter is smaller than the null value. It is two-sided if it states that the parameter is different from the null hypothesis value (it could be either larger or smaller). ü Hypotheses always refer to a population, not to a sample. Be sure to state H 0 and Ha in terms of population parameters. ü It is never correct to write a hypothesis about a sample statistic, such as Significance Tests: The Basics In any significance test, the null hypothesis has the form H 0 : parameter = value + n Stating

Studying Job Satisfaction a) Describe the parameter of interest in this setting. The parameter of interest is the mean µ of the differences (self-paced minus machine-paced) in job satisfaction scores in the population of all assembly-line workers at this company. b) State appropriate hypotheses for performing a significance test. Because the initial question asked whether job satisfaction differs, the alternative hypothesis is two-sided; that is, either µ < 0 or µ > 0. For simplicity, we write this as µ ≠ 0. That is, H 0 : µ = 0 Ha : µ ≠ 0 Significance Tests: The Basics Does the job satisfaction of assembly-line workers differ when their work is machinepaced rather than self-paced? One study chose 18 subjects at random from a company with over 200 workers who assembled electronic devices. Half of the workers were assigned at random to each of two groups. Both groups did similar assembly work, but one group was allowed to pace themselves while the other group used an assembly line that moved at a fixed pace. After two weeks, all the workers took a test of job satisfaction. Then they switched work setups and took the test again after two more weeks. The response variable is the difference in satisfaction scores, self-paced minus machine-paced. + n Example:

P-Values Definition: The probability, computed assuming H 0 is true, that the statistic would take a value as extreme as or more extreme than the one actually observed is called the P-value of the test. The smaller the P-value, the stronger the evidence against H 0 provided by the data. ü Small P-values are evidence against H 0 because they say that the observed result is unlikely to occur when H 0 is true. ü Large P-values fail to give convincing evidence against H 0 because they say that the observed result is likely to occur by chance when H 0 is true. Significance Tests: The Basics The null hypothesis H 0 states the claim that we are seeking evidence against. The probability that measures the strength of the evidence against a null hypothesis is called a P-value. + n Interpreting

Studying Job Satisfaction a) Explain what it means for the null hypothesis to be true in this setting. In this setting, H 0: µ = 0 says that the mean difference in satisfaction scores (self-paced - machine-paced) for the entire population of assembly -line workers at the company is 0. If H 0 is true, then the workers don’t favor one work environment over the other, on average. b) Interpret the P-value in context. Significance Tests: The Basics For the job satisfaction study, the hypotheses are H 0 : µ = 0 Ha : µ ≠ 0 + n Example: ü The P-value is the probability of observing a sample result as extreme or more extreme in the direction specified by Ha just by chance when H 0 is actually true. An outcome that would occur so often just by chance (almost 1 in every 4 random samples of 18 workers) when ü H 0 is true is not convincing evidence against H 0. We fail to reject H 0: µ = 0.

Significance ü If our sample result is too unlikely to have happened by chance assuming H 0 is true, then we’ll reject H 0. ü Otherwise, we will fail to reject H 0. Note: A fail-to-reject H 0 decision in a significance test doesn’t mean that H 0 is true. For that reason, you should never “accept H 0” or use language implying that you believe H 0 is true. In a nutshell, our conclusion in a significance test comes down to P-value small → reject H 0 → conclude Ha (in context) P-value large → fail to reject H 0 → cannot conclude Ha (in context) Significance Tests: The Basics The final step in performing a significance test is to draw a conclusion about the competing claims you were testing. We will make one of two decisions based on the strength of the evidence against the null hypothesis (and in favor of the alternative hypothesis) -- reject H 0 or fail to reject H 0. + n Statistical

Significance Definition: If the P-value is smaller than alpha, we say that the data are statistically significant at level α. In that case, we reject the null hypothesis H 0 and conclude that there is convincing evidence in favor of the alternative hypothesis Ha. When we use a fixed level of significance to draw a conclusion in a significance test, P-value < α → reject H 0 → conclude Ha (in context) P-value ≥ α → fail to reject H 0 → cannot conclude Ha (in context) Significance Tests: The Basics There is no rule for how small a P-value we should require in order to reject H 0 — it’s a matter of judgment and depends on the specific circumstances. But we can compare the P-value with a fixed value that we regard as decisive, called the significance level. We write it as α, the Greek letter alpha. When our P-value is less than the chosen α, we say that the result is statistically significant. + n Statistical

Better Batteries a) What conclusion can you make for the significance level α = 0. 05? Since the P-value, 0. 0276, is less than α = 0. 05, the sample result is statistically significant at the 5% level. We have sufficient evidence to reject H 0 and conclude that the company’s deluxe AAA batteries last longer than 30 hours, on average. b) What conclusion can you make for the significance level α = 0. 01? Since the P-value, 0. 0276, is greater than α = 0. 01, the sample result is not statistically significant at the 1% level. We do not have enough evidence to reject H 0 in this case. therefore, we cannot conclude that the deluxe AAA batteries last longer than 30 hours, on average. Significance Tests: The Basics A company has developed a new deluxe AAA battery that is supposed to last longer than its regular AAA battery. However, these new batteries are more expensive to produce, so the company would like to be convinced that they really do last longer. Based on years of experience, the company knows that its regular AAA batteries last for 30 hours of continuous use, on average. The company selects an SRS of 15 new batteries and uses them continuously until they are completely drained. A significance test is performed using the hypotheses H 0 : µ = 30 hours Ha : µ > 30 hours where µ is the true mean lifetime of the new deluxe AAA batteries. The resulting Pvalue is 0. 0276. + n Example:

I and Type II Errors + n Type Definition: If we reject H 0 when H 0 is true, we have committed a Type I error. If we fail to reject H 0 when H 0 is false, we have committed a Type II error. Truth about the population Conclusion based on sample H 0 true H 0 false (Ha true) Reject H 0 Type I error Correct conclusion Fail to reject H 0 Correct conclusion Type II error Significance Tests: The Basics When we draw a conclusion from a significance test, we hope our conclusion will be correct. But sometimes it will be wrong. There are two types of mistakes we can make. We can reject the null hypothesis when it’s actually true, known as a Type I error, or we can fail to reject a false null hypothesis, which is a Type II error.

Perfect Potatoes Describe a Type I and a Type II error in this setting, and explain the consequences of each. • A Type I error would occur if the producer concludes that the proportion of potatoes with blemishes is greater than 0. 08 when the actual proportion is 0. 08 (or less). Consequence: The potato-chip producer sends the truckload of acceptable potatoes away, which may result in lost revenue for the supplier. • A Type II error would occur if the producer does not send the truck away when more than 8% of the potatoes in the shipment have blemishes. Consequence: The producer uses the truckload of potatoes to make potato chips. More chips will be made with blemished potatoes, which may upset consumers. Significance Tests: The Basics A potato chip producer and its main supplier agree that each shipment of potatoes must meet certain quality standards. If the producer determines that more than 8% of the potatoes in the shipment have “blemishes, ” the truck will be sent away to get another load of potatoes from the supplier. Otherwise, the entire truckload will be used to make potato chips. To make the decision, a supervisor will inspect a random sample of potatoes from the shipment. The producer will then perform a significance test using the hypotheses H 0 : p = 0. 08 Ha : p > 0. 08 where p is the actual proportion of potatoes with blemishes in a given truckload. + n Example:

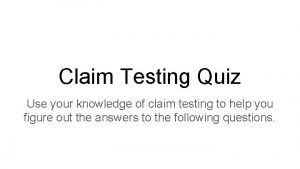
Probabilities + n Error For the truckload of potatoes in the previous example, we were testing H 0 : p = 0. 08 Ha : p > 0. 08 where p is the actual proportion of potatoes with blemishes. Suppose that the potato-chip producer decides to carry out this test based on a random sample of 500 potatoes using a 5% significance level (α = 0. 05). Significance Tests: The Basics We can assess the performance of a significance test by looking at the probabilities of the two types of error. That’s because statistical inference is based on asking, “What would happen if I did this many times? ” The shaded area in the right tail is 5%. Sample proportion values to the right of the green line at 0. 0999 will cause us to reject H 0 even though H 0 is true. This will happen in 5% of all possible samples. That is, P(making a Type I error) = 0. 05.

Probabilities Significance and Type I Error The significance level α of any fixed level test is the probability of a Type I error. That is, α is the probability that the test will reject the null hypothesis H 0 when H 0 is in fact true. Consider the consequences of a Type I error before choosing a significance level. What about Type II errors? A significance test makes a Type II error when it fails to reject a null hypothesis that really is false. There are many values of the parameter that satisfy the alternative hypothesis, so we concentrate on one value. We can calculate the probability that a test does reject H 0 when an alternative is true. This probability is called the power of the test against that specific alternative. Definition: The power of a test against a specific alternative is the probability that the test will reject H 0 at a chosen significance level α when the specified alternative value of the parameter is true. Significance Tests: The Basics The probability of a Type I error is the probability of rejecting H 0 when it is really true. As we can see from the previous example, this is exactly the significance level of the test. + n Error

Probabilities + n Error What if p = 0. 11? Earlier, we decided to reject H 0 at α = 0. 05 if our sample yielded a sample proportion to the right of the green line. Power and Type II Error The power of a test against any alternative is 1 minus the probability of a Type II error for that alternative; that is, power = 1 - β. Significance Tests: The Basics The potato-chip producer wonders whether the significance test of H 0 : p = 0. 08 versus Ha : p > 0. 08 based on a random sample of 500 potatoes has enough power to detect a shipment with, say, 11% blemished potatoes. In this case, a particular Type II error is to fail to reject H 0 : p = 0. 08 when p = 0. 11. Since we reject H 0 at α= 0. 05 if our sample yields a proportion > 0. 0999, we’d correctly reject the shipment about 75% of the time.

Studies: The Power of a Statistical Test Here Summary are the of influences questions we on the must question answer“How to decide manyhow many observations we do Ineed: need? ” 1. • If. Significance you insist onlevel. a smaller How significance much protection leveldo (such we want as 1% against rathera Type than 5%), I error you — have getting to a take significant a largerresult sample. from A our smaller sample when H significance true? requires stronger evidence to reject the null 0 is actuallylevel hypothesis. 2. Practical importance. How large a difference between the hypothesized • If you insist on parameter higher power value(such and the as actual 99% rather parameter than 90%), value is you important will needinapractice? larger sample. Higher power gives a better chance detecting a difference when really 3. Power. of. How confident do we want to itbeis that ourthere. study will detect • At anya significance difference oflevel the size and we desired think power, is important? detecting a small difference requires a larger sample than detecting a large difference. Significance Tests: The Basics How large a sample should we take when we plan to carry out a significance test? The answer depends on what alternative values of the parameter are important to detect. + n Planning

+ Tests About a Population Proportion Learning Objectives After this section, you should be able to… ü CHECK conditions for carrying out a test about a population proportion. ü CONDUCT a significance test about a population proportion. ü CONSTRUCT a confidence interval to draw a conclusion about for a two-sided test about a population proportion.

Section 9. 1 presented the reasoning of significance tests, including the idea of a P-value. In this section, we focus on the details of testing a claim about a population proportion. We’ll learn how to perform one-sided and two-sided tests about a population proportion. We’ll also see how confidence intervals and two-sided tests are related. Tests About a Population Proportion Confidence intervals and significance tests are based on the sampling distributions of statistics. That is, both use probability to say what would happen if we applied the inference method many times. + n Introduction

Out a Significance Test Does it provide convincing evidence against his claim? To find out, we must perform a significance test of H 0: p = 0. 80 Ha: p < 0. 80 where p = the actual proportion of free throws the shooter makes in the long run. Check Conditions: In Chapter 8, we introduced three conditions that should be met before we construct a confidence interval for an unknown population proportion: Random, Normal, and Independent. These same three conditions must be verified before carrying out a significance test. ü Random We can view this set of 50 shots as a simple random sample from the population of all possible shots that the player takes. ü Normal Assuming H 0 is true, p = 0. 80. then np = (50)(0. 80) = 40 and n (1 - p) = (50)(0. 20) = 10 are both at least 10, so the normal condition is met. ü Independent In our simulation, the outcome of each shot does is determined by a random number generator, so individual observations are independent. Tests About a Population Proportion Recall our basketball player who claimed to be an 80% free-throw shooter. In an SRS of 50 free-throws, he made 32. His sample proportion of made shots, 32/50 = 0. 64, is much lower than what he claimed. + n Carrying

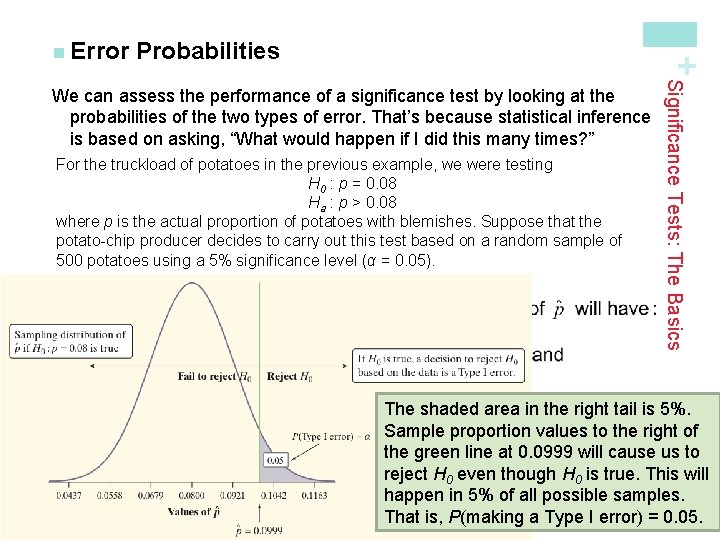
Out a Significance Test Calculations: Test statistic and P-value A significance test uses sample data to measure the strength of evidence against H 0. Here are some principles that apply to most tests: • The test compares a statistic calculated from sample data with the value of the parameter stated by the null hypothesis. • Values of the statistic far from the null parameter value in the direction specified by the alternative hypothesis give evidence against H 0. Definition: A test statistic measures how far a sample statistic diverges from what we would expect if the null hypothesis H 0 were true, in standardized units. That is Test About a Population Proportion If the null hypothesis H 0 : p = 0. 80 is true, then the player’s sample proportion of made free throws in an SRS of 50 shots would vary according to an approximately Normal sampling distribution with mean + n Carrying

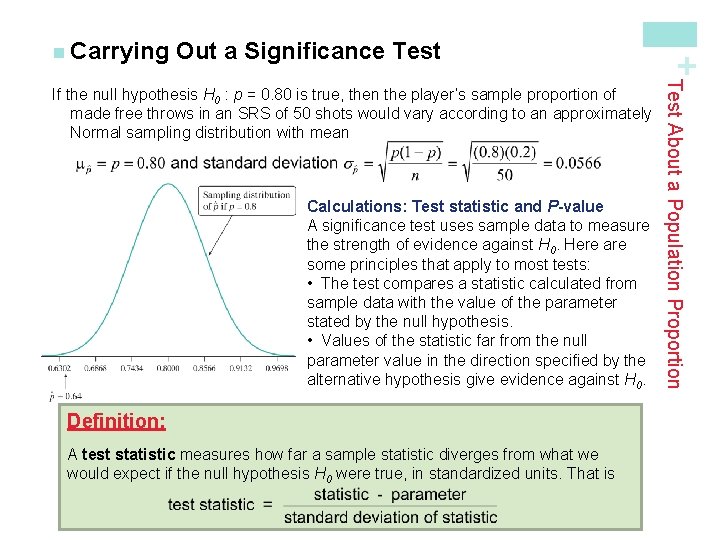
Out a Hypothesis Test The shaded area under the curve in (a) shows the P -value. (b) shows the corresponding area on the standard Normal curve, which displays the distribution of the z test statistic. Using Table A, we find that the P-value is P(z ≤ – 2. 83) = 0. 0023. So if H 0 is true, and the player makes 80% of his free throws in the long run, there’s only about a 2 -in-1000 chance that the player would make as few as 32 of 50 shots. Tests About a Population Proportion The test statistic says how far the sample result is from the null parameter value, and in what direction, on a standardized scale. You can use the test statistic to find the P-value of the test. In our free-throw shooter example, the sample proportion 0. 64 is pretty far below the hypothesized value H 0: p = 0. 80. Standardizing, we get + n Carrying

One-Sample z Test for a Proportion State: What hypotheses do you want to test, and at what significance level? Define any parameters you use. Plan: Choose the appropriate inference method. Check conditions. Do: If the conditions are met, perform calculations. • Compute the test statistic. • Find the P-value. Conclude: Interpret the results of your test in the context of the problem. When the conditions are met—Random, Normal, and Independent, When performing a significance test, however, the null hypothesis specifies a value for p, which we will call p 0. We assume that this value is correct when performing our calculations. Tests About a Population Proportion Significance Tests: A Four-Step Process + n The

One-Sample z Test for a Proportion Choose an SRS of size n from a large population that contains an unknown proportion p of successes. To test the hypothesis H 0 : p = p 0, compute the z statistic Use this test only when the expected numbers of successes and failures np 0 and n(1 - p 0) are Find the P-value by calculating the probability of getting a z statistic this large both at least 10 and the population or larger in the direction specified by the alternative hypothesis Ha: is at least 10 times as large as the sample. Tests About a Population Proportion The z statistic has approximately the standard Normal distribution when H 0 is true. P-values therefore come from the standard Normal distribution. Here is a summary of the details for a one-sample z test for a proportion. + n The

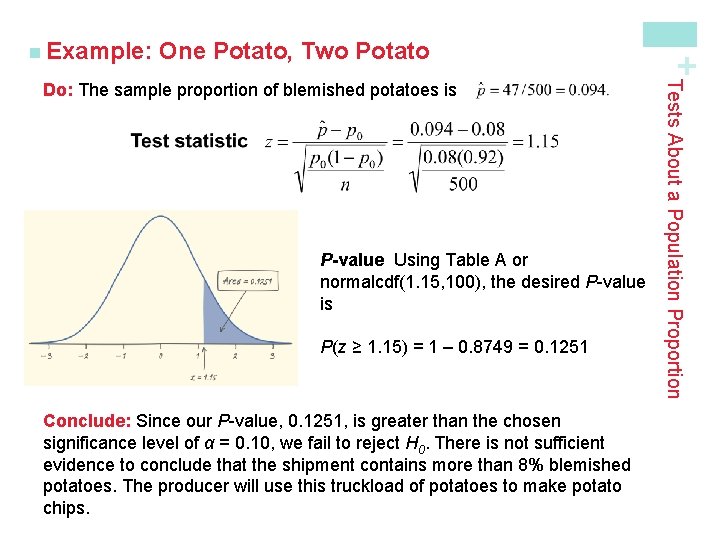
One Potato, Two Potato State: We want to perform at test at the α = 0. 10 significance level of H 0: p = 0. 08 Ha: p > 0. 08 where p is the actual proportion of potatoes in this shipment with blemishes. Plan: If conditions are met, we should do a one-sample z test for the population proportion p. üRandom The supervisor took a random sample of 500 potatoes from the shipment. üNormal Assuming H 0: p = 0. 08 is true, the expected numbers of blemished and unblemished potatoes are np 0 = 500(0. 08) = 40 and n(1 - p 0) = 500(0. 92) = 460, respectively. Because both of these values are at least 10, we should be safe doing Normal calculations. üIndependent Because we are sampling without replacement, we need to check the 10% condition. It seems reasonable to assume that there at least 10(500) = 5000 potatoes in the shipment. Tests About a Population Proportion A potato-chip producer has just received a truckload of potatoes from its main supplier. If the producer determines that more than 8% of the potatoes in the shipment have blemishes, the truck will be sent away to get another load from the supplier. A supervisor selects a random sample of 500 potatoes from the truck. An inspection reveals that 47 of the potatoes have blemishes. Carry out a significance test at the α= 0. 10 significance level. What should the producer conclude? + n Example:

One Potato, Two Potato P-value Using Table A or normalcdf(1. 15, 100), the desired P-value is P(z ≥ 1. 15) = 1 – 0. 8749 = 0. 1251 Conclude: Since our P-value, 0. 1251, is greater than the chosen significance level of α = 0. 10, we fail to reject H 0. There is not sufficient evidence to conclude that the shipment contains more than 8% blemished potatoes. The producer will use this truckload of potatoes to make potato chips. Tests About a Population Proportion Do: The sample proportion of blemished potatoes is + n Example:

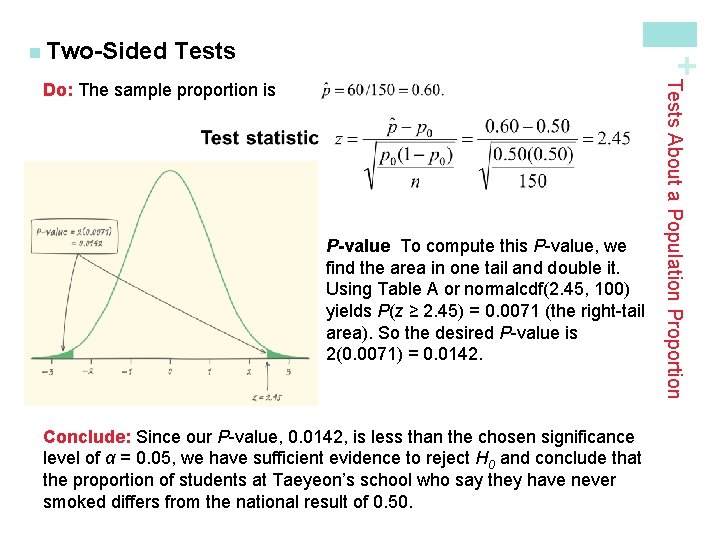
Tests State: We want to perform at test at the α = 0. 05 significance level of H 0: p = 0. 50 Ha: p ≠ 0. 50 where p is the actual proportion of students in Taeyeon’s school who would say they have never smoked cigarettes. Plan: If conditions are met, we should do a one-sample z test for the population proportion p. üRandom Taeyeon surveyed an SRS of 150 students from his school. üNormal Assuming H 0: p = 0. 50 is true, the expected numbers of smokers and nonsmokers in the sample are np 0 = 150(0. 50) = 75 and n(1 - p 0) = 150(0. 50) = 75. Because both of these values are at least 10, we should be safe doing Normal calculations. üIndependent We are sampling without replacement, we need to check the 10% condition. It seems reasonable to assume that there at least 10(150) = 1500 students a large high school. Tests About a Population Proportion According to the Centers for Disease Control and Prevention (CDC) Web site, 50% of high school students have never smoked a cigarette. Taeyeon wonders whether this national result holds true in his large, urban high school. For his AP Statistics class project, Taeyeon surveys an SRS of 150 students from his school. He gets responses from all 150 students, and 90 say that they have never smoked a cigarette. What should Taeyeon conclude? Give appropriate evidence to support your answer. + n Two-Sided

Tests + n Two-Sided P-value To compute this P-value, we find the area in one tail and double it. Using Table A or normalcdf(2. 45, 100) yields P(z ≥ 2. 45) = 0. 0071 (the right-tail area). So the desired P-value is 2(0. 0071) = 0. 0142. Conclude: Since our P-value, 0. 0142, is less than the chosen significance level of α = 0. 05, we have sufficient evidence to reject H 0 and conclude that the proportion of students at Taeyeon’s school who say they have never smoked differs from the national result of 0. 50. Tests About a Population Proportion Do: The sample proportion is

Confidence Intervals Give More Information Taeyeon found that 90 of an SRS of 150 students said that they had never smoked a cigarette. Before we construct a confidence interval for the population proportion p, we should check that both the number of successes and failures are at least 10. üThe number of successes and the number of failures in the sample are 90 and 60, respectively, so we can proceed with calculations. Our 95% confidence interval is: We are 95% confident that the interval from 0. 522 to 0. 678 captures the true proportion of students at Taeyeon’s high school who would say that they have never smoked a cigarette. Tests About a Population Proportion The result of a significance test is basically a decision to reject H 0 or fail to reject H 0. When we reject H 0, we’re left wondering what the actual proportion p might be. A confidence interval might shed some light on this issue. + n Why

Intervals and Two-Sided Tests level α (say, α = 0. 05) and a 100(1 – α)% confidence interval (a 95% confidence interval if α = 0. 05) give similar information about the population parameter. ü the sample proportion falls in the ü If. However, if the sample proportion “fail H 0” region, like the fallstoinreject the “reject H 0” region, the green value in confidence the figure, the resulting 95% interval resulting confidence interval would not 95% include p 0. In that case, would include p 0. In that both the significance testcase, and the significance testwould and the confidence interval provide confidence interval would unable evidence that p 0 is not thebe parameter to rule out p 0 as a plausible value. parameter value. Tests About a Population Proportion There is a link between confidence intervals and two-sided tests. The 95% confidence interval gives an approximate range of p 0’s that would not be rejected by a two-sided test at the α = 0. 05 significance level. The link isn’t perfect because the standard error used for the confidence interval is based on the sample proportion, while the denominator of the test statistic is based on the value p 0 from the null hypothesis. ü A two-sided test at significance + n Confidence

+ Tests About a Population Mean Learning Objectives After this section, you should be able to… ü CHECK conditions for carrying out a test about a population mean. ü CONDUCT a one-sample t test about a population mean. ü CONSTRUCT a confidence interval to draw a conclusion for a twosided test about a population mean. ü PERFORM significance tests for paired data.

Inference about a population mean µ uses a t distribution with n - 1 degrees of freedom, except in the rare case when the population standard deviation σ is known. We learned how to construct confidence intervals for a population mean in Section 8. 3. Now we’ll examine the details of testing a claim about an unknown parameter µ. Tests About a Population Mean Confidence intervals and significance tests for a population proportion p are based on z-values from the standard Normal distribution. + n Introduction

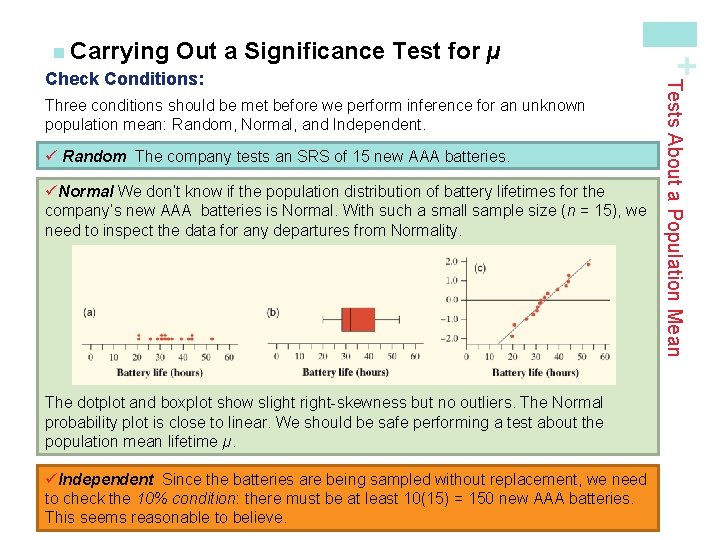
Out a Significance Test for µ To find out, we must perform a significance test of H 0: µ = 30 hours Ha: µ > 30 hours where µ = the true mean lifetime of the new deluxe AAA batteries. Check Conditions: Three conditions should be met before we perform inference for an unknown population mean: Random, Normal, and Independent. The Normal condition for means is Population distribution is Normal or sample size is large (n ≥ 30) We often don’t know whether the population distribution is Normal. But if the sample size is large (n ≥ 30), we can safely carry out a significance test (due to the central limit theorem). If the sample size is small, we should examine the sample data for any obvious departures from Normality, such as skewness and outliers. Tests About a Population Mean In an earlier example, a company claimed to have developed a new AAA battery that lasts longer than its regular AAA batteries. Based on years of experience, the company knows that its regular AAA batteries last for 30 hours of continuous use, on average. An SRS of 15 new batteries lasted an average of 33. 9 hours with a standard deviation of 9. 8 hours. Do these data give convincing evidence that the new batteries last longer on average? + n Carrying

Three conditions should be met before we perform inference for an unknown population mean: Random, Normal, and Independent. ü Random The company tests an SRS of 15 new AAA batteries. üNormal We don’t know if the population distribution of battery lifetimes for the company’s new AAA batteries is Normal. With such a small sample size (n = 15), we need to inspect the data for any departures from Normality. The dotplot and boxplot show slight right-skewness but no outliers. The Normal probability plot is close to linear. We should be safe performing a test about the population mean lifetime µ. üIndependent Since the batteries are being sampled without replacement, we need to check the 10% condition: there must be at least 10(15) = 150 new AAA batteries. This seems reasonable to believe. + a Significance Test for µ Tests About a Population Mean n Carrying Out Check Conditions:

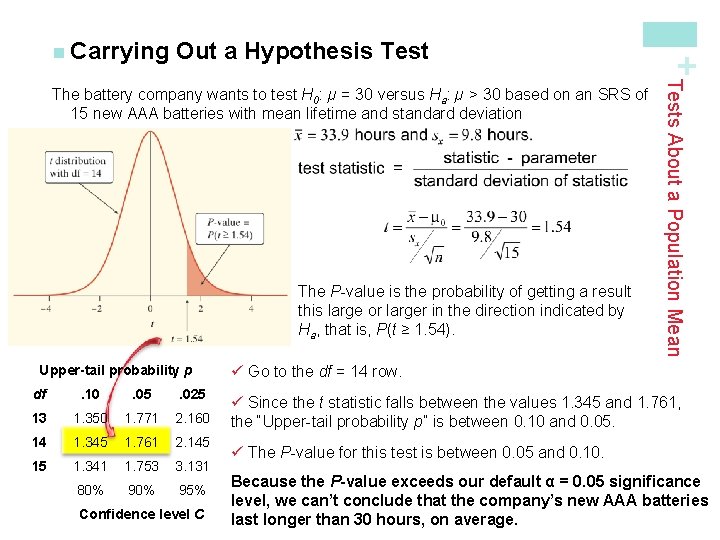
Out a Significance Test For a test of H 0: µ = µ 0, our statistic is the sample mean. Its standard deviation is Because the population standard deviation σ is usually unknown, we use the sample standard deviation sx in its place. The resulting test statistic has the standard error of the sample mean in the denominator When the Normal condition is met, this statistic has a t distribution with n - 1 degrees of freedom. Test About a Population Mean Calculations: Test statistic and P-value When performing a significance test, we do calculations assuming that the null hypothesis H 0 is true. The test statistic measures how far the sample result diverges from the parameter value specified by H 0, in standardized units. As before, + n Carrying

Out a Hypothesis Test The P-value is the probability of getting a result this large or larger in the direction indicated by Ha, that is, P(t ≥ 1. 54). Upper-tail probability p df . 10 . 05 . 025 13 1. 350 1. 771 2. 160 14 1. 345 1. 761 2. 145 15 1. 341 1. 753 3. 131 80% 95% Confidence level C Tests About a Population Mean The battery company wants to test H 0: µ = 30 versus Ha: µ > 30 based on an SRS of 15 new AAA batteries with mean lifetime and standard deviation + n Carrying ü Go to the df = 14 row. ü Since the t statistic falls between the values 1. 345 and 1. 761, the “Upper-tail probability p” is between 0. 10 and 0. 05. ü The P-value for this test is between 0. 05 and 0. 10. Because the P-value exceeds our default α = 0. 05 significance level, we can’t conclude that the company’s new AAA batteries last longer than 30 hours, on average.

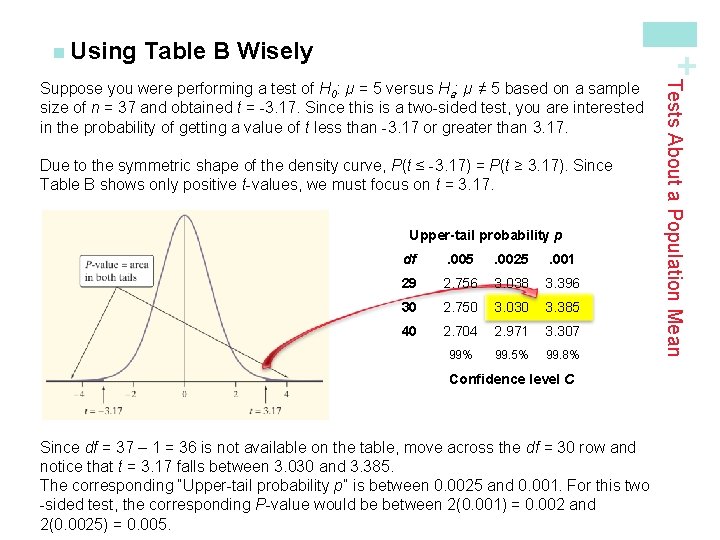
Table B Wisely • Table B has other limitations for finding P-values. It includes probabilities only for t distributions with degrees of freedom from 1 to 30 and then skips to df = 40, 50, 60, 80, 100, and 1000. (The bottom row gives probabilities for df = ∞, which corresponds to the standard Normal curve. ) Note: If the df you need isn’t provided in Table B, use the next lower df that is available. • Table B shows probabilities only for positive values of t. To find a Pvalue for a negative value of t, we use the symmetry of the t distributions. Tests About a Population Mean • Table B gives a range of possible P-values for a significance. We can still draw a conclusion from the test in much the same way as if we had a single probability by comparing the range of possible P-values to our desired significance level. + n Using

Table B Wisely + n Using Due to the symmetric shape of the density curve, P(t ≤ -3. 17) = P(t ≥ 3. 17). Since Table B shows only positive t-values, we must focus on t = 3. 17. Upper-tail probability p df . 005 . 0025 . 001 29 2. 756 3. 038 3. 396 30 2. 750 3. 030 3. 385 40 2. 704 2. 971 3. 307 99% 99. 5% 99. 8% Confidence level C Since df = 37 – 1 = 36 is not available on the table, move across the df = 30 row and notice that t = 3. 17 falls between 3. 030 and 3. 385. The corresponding “Upper-tail probability p” is between 0. 0025 and 0. 001. For this two -sided test, the corresponding P-value would be between 2(0. 001) = 0. 002 and 2(0. 0025) = 0. 005. Tests About a Population Mean Suppose you were performing a test of H 0: µ = 5 versus Ha: µ ≠ 5 based on a sample size of n = 37 and obtained t = -3. 17. Since this is a two-sided test, you are interested in the probability of getting a value of t less than -3. 17 or greater than 3. 17.

One-Sample t Test Choose an SRS of size n from a large population that contains an unknown mean µ. To test the hypothesis H 0 : µ = µ 0, compute the one-sample t statistic Use this test only when (1) the population distribution is Normal or the sample is large Find the P-value by calculating the probability of getting a t statistic this large ≥ 30), specified and (2) the population at or larger in the(n direction by the alternative is hypothesis Ha in a tdistribution with df least = n - 110 times as large as the sample. Tests About a Population Mean When the conditions are met, we can test a claim about a population mean µ using a one-sample t test. + n The

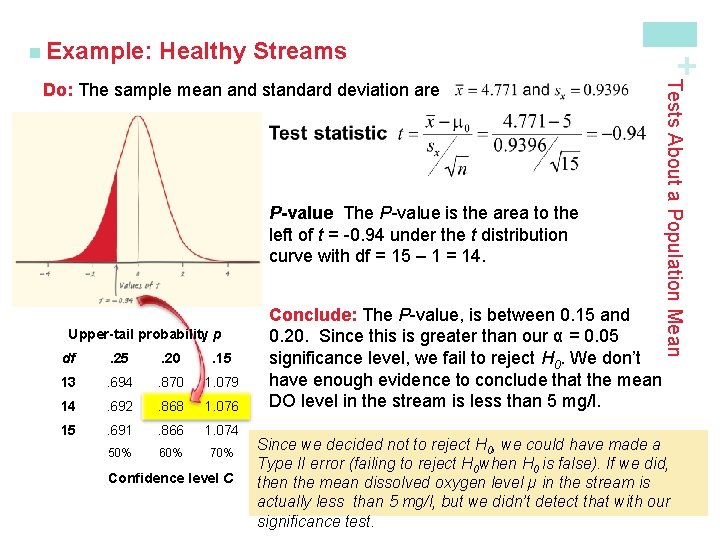
Healthy Streams + n Example: 4. 53 5. 42 5. 04 6. 38 3. 29 4. 01 5. 23 4. 66 4. 13 2. 87 5. 50 5. 73 4. 83 5. 55 4. 40 A dissolved oxygen level below 5 mg/l puts aquatic life at risk. State: We want to perform a test at the α = 0. 05 significance level of H 0 : µ = 5 Ha : µ < 5 where µ is the actual mean dissolved oxygen level in this stream. Plan: If conditions are met, we should do a one-sample t test for µ. üRandom The researcher measured the DO level at 15 randomly chosen locations. Tests About a Population Mean The level of dissolved oxygen (DO) in a stream or river is an important indicator of the water’s ability to support aquatic life. A researcher measures the DO level at 15 randomly chosen locations along a stream. Here are the results in milligrams per liter: üNormal We don’t know whether the population distribution of DO levels at all points along the stream is Normal. With such a small sample size (n = 15), we need to look at the data to see if it’s safe to use t procedures. üIndependent There is an infinite number of The histogram looks roughly symmetric; the possible locations along the stream, so it isn’t boxplot shows no outliers; and the Normal necessary to check the 10% condition. We do probability plot is fairly linear. With no outliers need to assume that individual or strong skewness, the t procedures should measurements are independent. be pretty accurate even if the population distribution isn’t Normal.

Healthy Streams P-value The P-value is the area to the left of t = -0. 94 under the t distribution curve with df = 15 – 1 = 14. Upper-tail probability p df . 25 . 20 . 15 13 . 694 . 870 1. 079 14 . 692 . 868 1. 076 15 . 691 . 866 1. 074 50% 60% 70% Confidence level C Conclude: The P-value, is between 0. 15 and 0. 20. Since this is greater than our α = 0. 05 significance level, we fail to reject H 0. We don’t have enough evidence to conclude that the mean DO level in the stream is less than 5 mg/l. Tests About a Population Mean Do: The sample mean and standard deviation are + n Example: Since we decided not to reject H 0, we could have made a Type II error (failing to reject H 0 when H 0 is false). If we did, then the mean dissolved oxygen level µ in the stream is actually less than 5 mg/l, but we didn’t detect that with our significance test.

Tests üIQR = Q 3 – Q 1 = 34. 115 – 29. 990 = 4. 125 üAny data value greater than Q 3 + 1. 5(IQR) or less than Q 1 – 1. 5(IQR) is considered an outlier. Q 3 + 1. 5(IQR) = 34. 115 + 1. 5(4. 125) = 40. 3025 Q 1 – 1. 5(IQR) = 29. 990 – 1. 5(4. 125) = 23. 0825 üSince the maximum value 35. 547 is less than 40. 3025 and the minimum value 26. 491 is greater than 23. 0825, there are no outliers. Tests About a Population Mean At the Hawaii Pineapple Company, managers are interested in the sizes of the pineapples grown in the company’s fields. Last year, the mean weight of the pineapples harvested from one large field was 31 ounces. A new irrigation system was installed in this field after the growing season. Managers wonder whether this change will affect the mean weight of future pineapples grown in the field. To find out, they select and weigh a random sample of 50 pineapples from this year’s crop. The Minitab output below summarizes the data. Determine whethere any outliers. + n Two-Sided

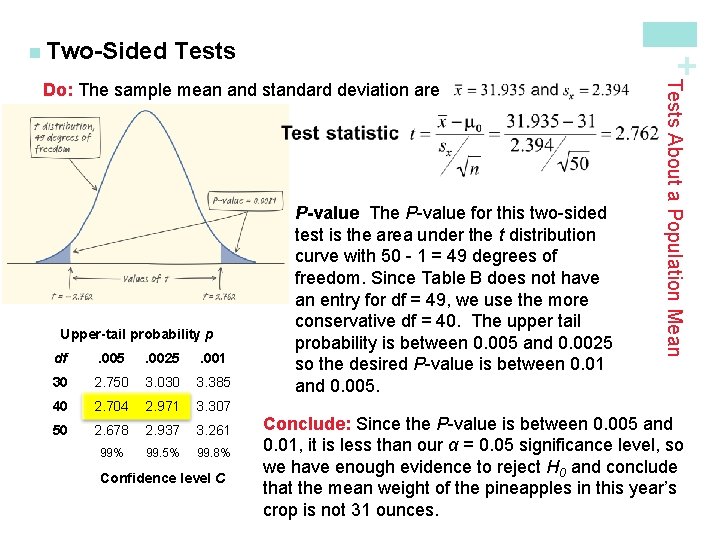
Tests where µ = the mean weight (in ounces) of all pineapples grown in the field this year. Since no significance level is given, we’ll use α = 0. 05. Plan: If conditions are met, we should do a one-sample t test for µ. üRandom The data came from a random sample of 50 pineapples from this year’s crop. üNormal We don’t know whether the population distribution of pineapple weights this year is Normally distributed. But n = 50 ≥ 30, so the large sample size (and the fact that there are no outliers) makes it OK to use t procedures. üIndependent There need to be at least 10(50) = 500 pineapples in the field because managers are sampling without replacement (10% condition). We would expect many more than 500 pineapples in a “large field. ” Tests About a Population Mean State: We want to test the hypotheses H 0: µ = 31 Ha: µ ≠ 31 + n Two-Sided

Tests + n Two-Sided Upper-tail probability p df . 005 . 0025 . 001 30 2. 750 3. 030 3. 385 40 2. 704 2. 971 3. 307 50 2. 678 2. 937 3. 261 99% 99. 5% 99. 8% Confidence level C P-value The P-value for this two-sided test is the area under the t distribution curve with 50 - 1 = 49 degrees of freedom. Since Table B does not have an entry for df = 49, we use the more conservative df = 40. The upper tail probability is between 0. 005 and 0. 0025 so the desired P-value is between 0. 01 and 0. 005. Tests About a Population Mean Do: The sample mean and standard deviation are Conclude: Since the P-value is between 0. 005 and 0. 01, it is less than our α = 0. 05 significance level, so we have enough evidence to reject H 0 and conclude that the mean weight of the pineapples in this year’s crop is not 31 ounces.

Intervals Give More Information The 95% confidence interval for the mean weight of all the pineapples grown in the field this year is 31. 255 to 32. 616 ounces. We are 95% confident that this interval captures the true mean weight µ of this year’s pineapple crop. Tests About a Population Mean Minitab output for a significance test and confidence interval based on the pineapple data is shown below. The test statistic and P-value match what we got earlier (up to rounding). + n Confidence As with proportions, there is a link between a two-sided test at significance level α and a 100(1 – α)% confidence interval for a population mean µ. For the pineapples, the two-sided test at α =0. 05 rejects H 0: µ = 31 in favor of Ha: µ ≠ 31. The corresponding 95% confidence interval does not include 31 as a plausible value of the parameter µ. In other words, the test and interval lead to the same conclusion about H 0. But the confidence interval provides much more information: a set of plausible values for the population mean.

Intervals and Two-Sided Tests ü A two-sided test at significance level α (say, α = 0. 05) and a 100(1 – α)% confidence interval (a 95% confidence interval if α = 0. 05) give similar information about the population parameter. ü When the two-sided significance test at level α rejects H 0: µ = µ 0, the 100(1 – α)% confidence interval for µ will not contain the hypothesized value µ 0. ü When the two-sided significance test at level α fails to reject the null hypothesis, the confidence interval for µ will contain µ 0. Tests About a Population Mean The connection between two-sided tests and confidence intervals is even stronger for means than it was for proportions. That’s because both inference methods for means use the standard error of the sample mean in the calculations. + n Confidence

for Means: Paired Data When paired data result from measuring the same quantitative variable twice, as in the job satisfaction study, we can make comparisons by analyzing the differences in each pair. If the conditions for inference are met, we can use one-sample t procedures to perform inference about the mean difference µd. These methods are sometimes called paired t procedures. Test About a Population Mean Comparative studies are more convincing than single-sample investigations. For that reason, one-sample inference is less common than comparative inference. Study designs that involve making two observations on the same individual, or one observation on each of two similar individuals, result in paired data. + n Inference

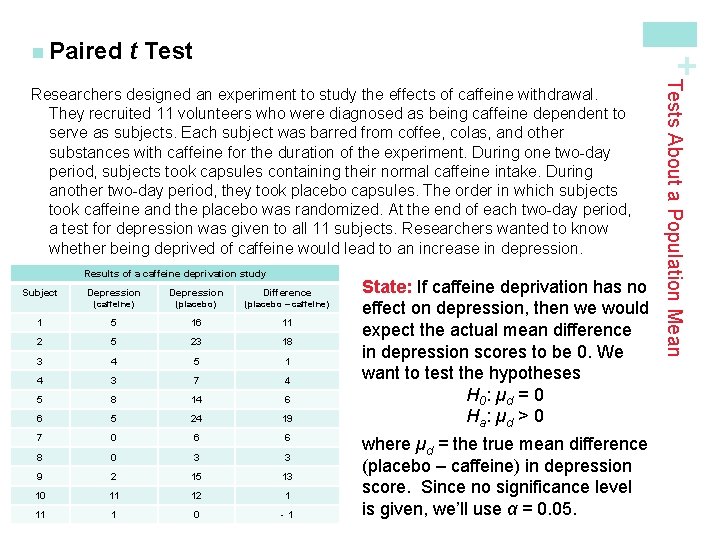
t Test + n Paired Results of a caffeine deprivation study Subject Depression Difference (caffeine) (placebo – caffeine) 1 5 16 11 2 5 23 18 3 4 5 1 4 3 7 4 5 8 14 6 6 5 24 19 7 0 6 6 8 0 3 3 9 2 15 13 10 11 12 1 11 1 0 -1 State: If caffeine deprivation has no effect on depression, then we would expect the actual mean difference in depression scores to be 0. We want to test the hypotheses H 0 : µd = 0 Ha : µd > 0 where µd = the true mean difference (placebo – caffeine) in depression score. Since no significance level is given, we’ll use α = 0. 05. Tests About a Population Mean Researchers designed an experiment to study the effects of caffeine withdrawal. They recruited 11 volunteers who were diagnosed as being caffeine dependent to serve as subjects. Each subject was barred from coffee, colas, and other substances with caffeine for the duration of the experiment. During one two-day period, subjects took capsules containing their normal caffeine intake. During another two-day period, they took placebo capsules. The order in which subjects took caffeine and the placebo was randomized. At the end of each two-day period, a test for depression was given to all 11 subjects. Researchers wanted to know whether being deprived of caffeine would lead to an increase in depression.

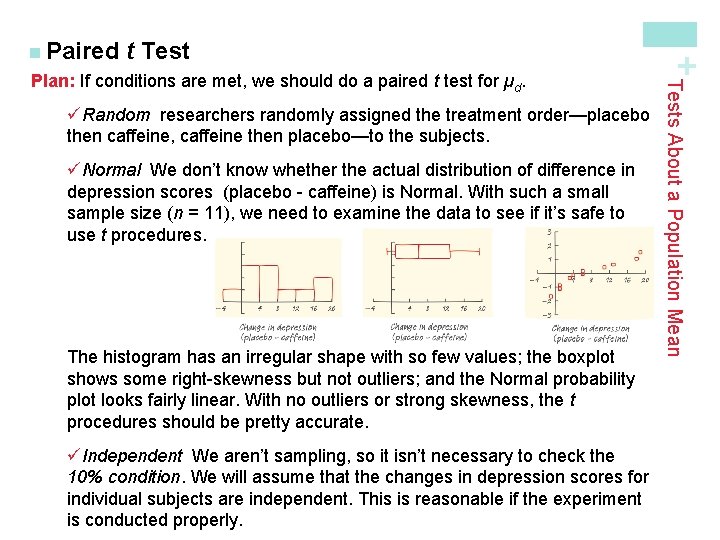
t Test üRandom researchers randomly assigned the treatment order—placebo then caffeine, caffeine then placebo—to the subjects. üNormal We don’t know whether the actual distribution of difference in depression scores (placebo - caffeine) is Normal. With such a small sample size (n = 11), we need to examine the data to see if it’s safe to use t procedures. The histogram has an irregular shape with so few values; the boxplot shows some right-skewness but not outliers; and the Normal probability plot looks fairly linear. With no outliers or strong skewness, the t procedures should be pretty accurate. üIndependent We aren’t sampling, so it isn’t necessary to check the 10% condition. We will assume that the changes in depression scores for individual subjects are independent. This is reasonable if the experiment is conducted properly. Tests About a Population Mean Plan: If conditions are met, we should do a paired t test for µd. + n Paired

t Test P-value According to technology, the area to the right of t = 3. 53 on the t distribution curve with df = 11 – 1 = 10 is 0. 0027. Conclude: With a P-value of 0. 0027, which is much less than our chosen α = 0. 05, we have convincing evidence to reject H 0: µd = 0. We can therefore conclude that depriving these caffeine-dependent subjects of caffeine caused an average increase in depression scores. Tests About a Population Mean Do: The sample mean and standard deviation are + n Paired

Tests Wisely Carrying out a significance test is often quite simple, especially if you use a calculator or computer. Using tests wisely is not so simple. Here are some points to keep in mind when using or interpreting significance tests. Statistical Significance and Practical Importance When a null hypothesis (“no effect” or “no difference”) can be rejected at the usual levels (α = 0. 05 or α = 0. 01), there is good evidence of a difference. But that difference may be very small. When large samples are available, even tiny deviations from the null hypothesis will be significant. Test About a Population Mean Significance tests are widely used in reporting the results of research in many fields. New drugs require significant evidence of effectiveness and safety. Courts ask about statistical significance in hearing discrimination cases. Marketers want to know whether a new ad campaign significantly outperforms the old one, and medical researchers want to know whether a new therapy performs significantly better. In all these uses, statistical significance is valued because it points to an effect that is unlikely to occur simply by chance. + n Using

Tests Wisely Statistical Inference Is Not Valid for All Sets of Data Badly designed surveys or experiments often produce invalid results. Formal statistical inference cannot correct basic flaws in the design. Each test is valid only in certain circumstances, with properly produced data being particularly important. Beware of Multiple Analyses Statistical significance ought to mean that you have found a difference that you were looking for. The reasoning behind statistical significance works well if you decide what difference you are seeking, design a study to search for it, and use a significance test to weigh the evidence you get. In other settings, significance may have little meaning. Test About a Population Mean Don’t Ignore Lack of Significance There is a tendency to infer that there is no difference whenever a P-value fails to attain the usual 5% standard. In some areas of research, small differences that are detectable only with large sample sizes can be of great practical significance. When planning a study, verify that the test you plan to use has a high probability (power) of detecting a difference of the size you hope to find. + n Using

+ Significance Tests: The Basics Summary In this section, we learned that… ü A significance test assesses the evidence provided by data against a null hypothesis H 0 in favor of an alternative hypothesis Ha. ü The hypotheses are stated in terms of population parameters. Often, H 0 is a statement of no change or no difference. Ha says that a parameter differs from its null hypothesis value in a specific direction (one-sided alternative) or in either direction (two-sided alternative). ü The reasoning of a significance test is as follows. Suppose that the null hypothesis is true. If we repeated our data production many times, would we often get data as inconsistent with H 0 as the data we actually have? If the data are unlikely when H 0 is true, they provide evidence against H 0. ü The P-value of a test is the probability, computed supposing H 0 to be true, that the statistic will take a value at least as extreme as that actually observed in the direction specified by Ha.

+ Significance Tests: The Basics Summary ü Small P-values indicate strong evidence against H 0. To calculate a P-value, we must know the sampling distribution of the test statistic when H 0 is true. There is no universal rule for how small a P-value in a significance test provides convincing evidence against the null hypothesis. ü If the P-value is smaller than a specified value α (called the significance level), the data are statistically significant at level α. In that case, we can reject H 0. If the P-value is greater than or equal to α, we fail to reject H 0. ü A Type I error occurs if we reject H 0 when it is in fact true. A Type II error occurs if we fail to reject H 0 when it is actually false. In a fixed level α significance test, the probability of a Type I error is the significance level α. ü The power of a significance test against a specific alternative is the probability that the test will reject H 0 when the alternative is true. Power measures the ability of the test to detect an alternative value of the parameter. For a specific alternative, P(Type II error) = 1 - power.

+ Tests About a Population Proportion Summary In this section, we learned that… ü As with confidence intervals, you should verify that the three conditions— Random, Normal, and Independent—are met before you carry out a significance test. ü Significance tests for H 0 : p = p 0 are based on the test statistic with P-values calculated from the standard Normal distribution. ü The one-sample z test for a proportion is approximately correct when (1) the data were produced by random sampling or random assignment; (2) the population is at least 10 times as large as the sample; and (3) the sample is large enough to satisfy np 0 ≥ 10 and n(1 - p 0) ≥ 10 (that is, the expected numbers of successes and failures are both at least 10).

+ Tests About a Population Proportion Summary In this section, we learned that… ü Follow the four-step process when you carry out a significance test: STATE: What hypotheses do you want to test, and at what significance level? Define any parameters you use. PLAN: Choose the appropriate inference method. Check conditions. DO: If the conditions are met, perform calculations. • Compute the test statistic. • Find the P-value. CONCLUDE: Interpret the results of your test in the context of the problem. ü Confidence intervals provide additional information that significance tests do not —namely, a range of plausible values for the true population parameter p. A two-sided test of H 0 : p = p 0 at significance level α gives roughly the same conclusion as a 100(1 – α)% confidence interval.

+ Tests About a Population Mean Summary In this section, we learned that… ü Significance tests for the mean µ of a Normal population are based on the sampling distribution of the sample mean. Due to the central limit theorem, the resulting procedures are approximately correct for other population distributions when the sample is large. ü If we somehow know σ, we can use a z test statistic and the standard Normal distribution to perform calculations. In practice, we typically do not know σ. Then, we use the one-sample t statistic with P-values calculated from the t distribution with n - 1 degrees of freedom.

+ Tests About a Population Mean Summary ü The one-sample t test is approximately correct when Random The data were produced by random sampling or a randomized experiment. Normal The population distribution is Normal OR the sample size is large (n ≥ 30). Independent Individual observations are independent. When sampling without replacement, check that the population is at least 10 times as large as the sample. ü Confidence intervals provide additional information that significance tests do not —namely, a range of plausible values for the parameter µ. A two-sided test of H 0: µ = µ 0 at significance level α gives the same conclusion as a 100(1 – α)% confidence interval for µ. ü Analyze paired data by first taking the difference within each pair to produce a single sample. Then use one-sample t procedures.

+ Tests About a Population Mean Summary ü Very small differences can be highly significant (small P-value) when a test is based on a large sample. A statistically significant difference need not be practically important. ü Lack of significance does not imply that H 0 is true. Even a large difference can fail to be significant when a test is based on a small sample. ü Significance tests are not always valid. Faulty data collection, outliers in the data, and other practical problems can invalidate a test. Many tests run at once will probably produce some significant results by chance alone, even if all the null hypotheses are true.
 Of value
Of value How to start off a counterclaim paragraph
How to start off a counterclaim paragraph Example of frequency claim
Example of frequency claim Examples of a claim statement
Examples of a claim statement Lesson 8.5 testing a claim about a mean
Lesson 8.5 testing a claim about a mean What is the claim in hypothesis testing
What is the claim in hypothesis testing Domain test means
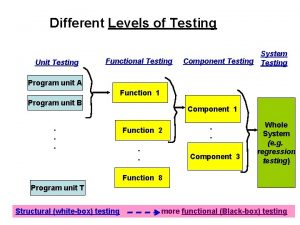
Domain test means Black-box testing disebut juga sebagai behavioral testing
Black-box testing disebut juga sebagai behavioral testing Static testing and dynamic testing
Static testing and dynamic testing Component testing is a black box testing
Component testing is a black box testing Decision table testing in software testing
Decision table testing in software testing Control structure testing in software testing
Control structure testing in software testing Motivational overview in software testing
Motivational overview in software testing Decision table testing is white box
Decision table testing is white box Anuj magazine
Anuj magazine Software domain examples
Software domain examples Decision table testing
Decision table testing Du path testing
Du path testing Rigorous testing in software testing
Rigorous testing in software testing Functional testing vs unit testing
Functional testing vs unit testing Jenis-jenis black box testing
Jenis-jenis black box testing Positive and negative testing
Positive and negative testing Testing blindness in software testing
Testing blindness in software testing What is testing
What is testing Disadvantages of god pod method
Disadvantages of god pod method Significance criteria
Significance criteria Limitations of macroeconomics
Limitations of macroeconomics Significance of the study
Significance of the study What is the significance of tessie's final scream
What is the significance of tessie's final scream Painted faces and long hair
Painted faces and long hair What is significance of the study
What is significance of the study Interphase description
Interphase description Babylon significance
Babylon significance Importance of mitosis
Importance of mitosis Discussion of saponification value of oil
Discussion of saponification value of oil What is independent variable in research
What is independent variable in research General to particular example sentence
General to particular example sentence Significance of mitosis
Significance of mitosis Significance of bragg's law
Significance of bragg's law Research meaning
Research meaning Historical context of hamlet
Historical context of hamlet Hypothesis
Hypothesis Why is microeconomics important
Why is microeconomics important Practical significance example
Practical significance example Reynolds number formula
Reynolds number formula Pcv
Pcv Refracting telescopes exhibit great focus and color.
Refracting telescopes exhibit great focus and color. Saponification value significance
Saponification value significance Significance of michaelis menten equation
Significance of michaelis menten equation History of stokes theorem
History of stokes theorem Economic significance of transportation
Economic significance of transportation Berlin wall
Berlin wall King philip's war apush significance
King philip's war apush significance Confidence level and significance level
Confidence level and significance level Gideon v wainwright significance
Gideon v wainwright significance Significance of knowledge management
Significance of knowledge management Bacon's rebellion significance
Bacon's rebellion significance Significance
Significance Which civilizations were the first to record measurements
Which civilizations were the first to record measurements Manpower planning types
Manpower planning types Chapter 10 section 3 acquiring new lands
Chapter 10 section 3 acquiring new lands Significance of operations research
Significance of operations research Light motif in a streetcar named desire
Light motif in a streetcar named desire