FLUID MECHANICS LAMINAR AND TURBULENT FLOW FLUID FLOW

FLUID MECHANICS LAMINAR AND TURBULENT FLOW

FLUID FLOW STREAMLINE – LAMINAR FLOW TURBULENT FLOW REYNOLDS NUMBER

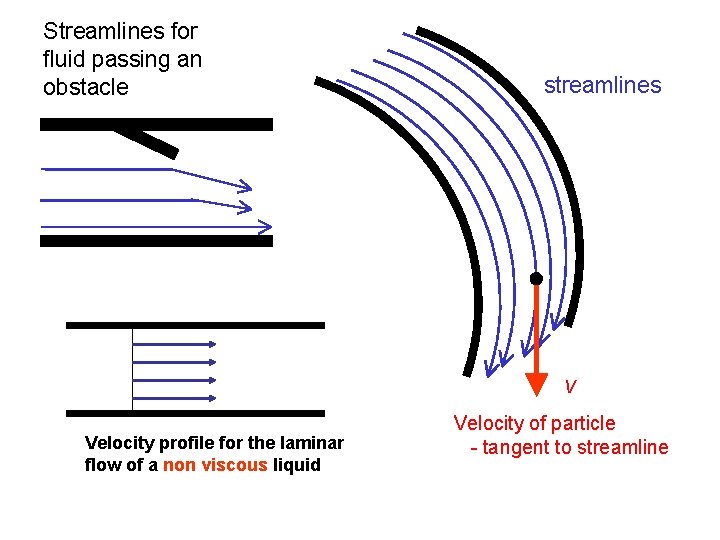
Streamlines for fluid passing an obstacle streamlines v Velocity profile for the laminar flow of a non viscous liquid Velocity of particle - tangent to streamline

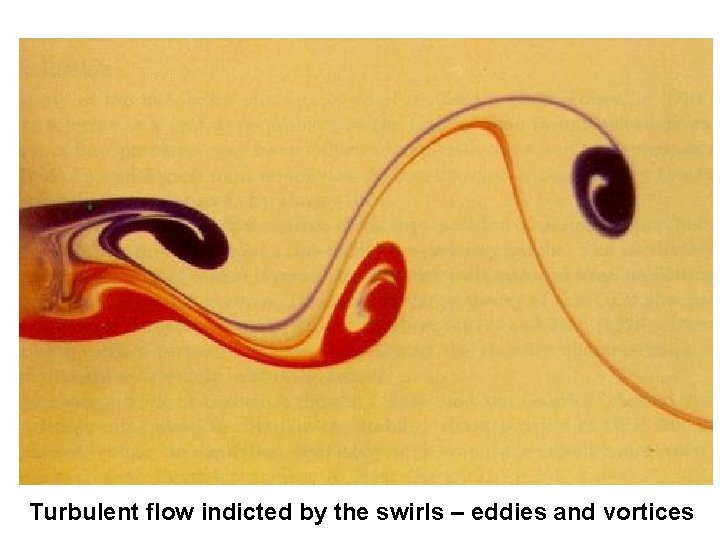
Turbulent flow indicted by the swirls – eddies and vortices

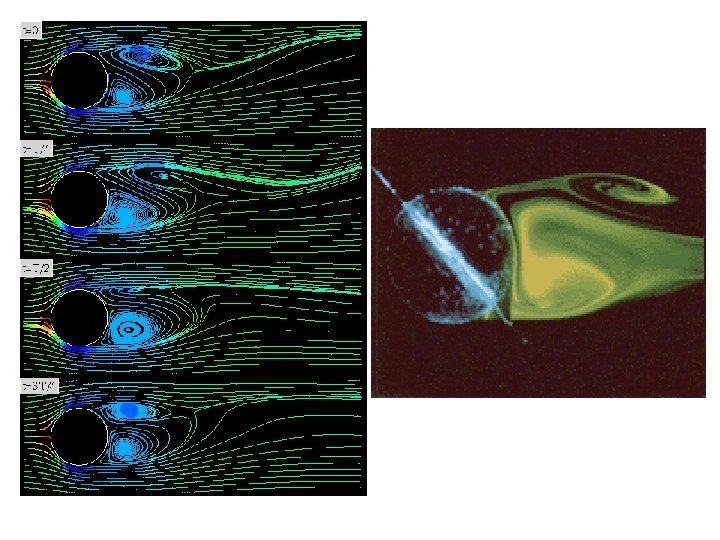
REYNOLDS NUMBER A British scientist Osborne Reynolds (1842 – 1912) established that the nature of the flow depends upon a dimensionless quantity, which is now called the Reynolds number Re. Re = v L / v L density of fluid average flow velocity over the cross section of the pipe dimension characterising a cross section

Re is a dimensionless number Re = v L / [Re] [kg. m-3] [m. s-1][m] [Pa. s]-1 [kg] [m-1][s-1][kg. m. s-2. m-2. s]-1 = [1] For a fluid flowing through a pipe – as a rule of thumb Re < ~ 2000 laminar flow ~ 2000 < Re < ~ 3000 unstable laminar / turbulent Re > ~ 2000 turbulent

Re = v L / Sydney Harbour Ferry

Re = v L / = 103 kg. m-3 Re = (103)(5)(10) / (10 -3) v = 5 m. s-1 Re = 5 x 107 L = 10 m = 10 -3 Pa. s

Spermatozoa swimming Re = v L /

Spermatozoa swimming Re = v L / = 103 kg. m-3 v = 10 -5 m. s-1 Re = (103)(10 -5)(10 x 10 -6) / (10 -3) L = 10 mm Re = 10 -4 = 10 -3 Pa. s

Household plumbing pipes Typical household pipes are about 30 mm in diameter and water flows at about 10 m. s-1 Re ~ (10)(30 10 -3)(103) / (10 -3) ~ 3 105 The circulatory system Speed of blood v ~ 0. 2 m. s-1 Diameter of the largest blood vessel, the aorta L ~ 10 mm Viscosity of blood probably ~ 10 -3 Pa. s (assume same as water) Re ~ (0. 2)(10 10 -3)(103) / 10 -3) ~ 2 103

The method of swimming is quite different for Fish (Re ~ 10 000) and sperm (Re ~ 0. 0001) Modes of boat propulsion which work in thin liquids (water) will not work in thick liquids (glycerine) It is possible to stir glycerine up, and then unstir it completely. You cannot do this with water.

FLUID FLOW IDEAL FLUID EQUATION OF CONTINUITY How can the blood deliver oxygen to body so successfully? How do we model fluids flowing in streamlined motion?

IDEAL FLUID Fluid motion is usually very complicated. However, by making a set of assumptions about the fluid, one can still develop useful models of fluid behaviour. An ideal fluid is Incompressible – the density is constant Irrotational – the flow is smooth, no turbulence Nonviscous – fluid has no internal friction ( = 0) Steady flow – the velocity of the fluid at each point is constant in time.

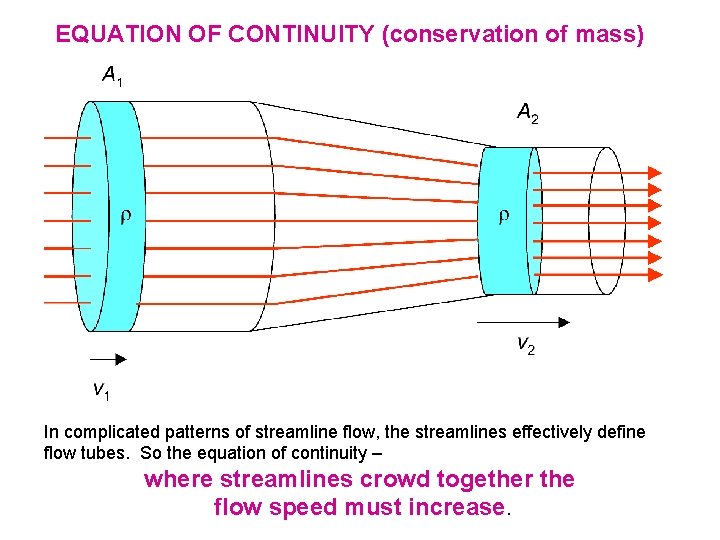
EQUATION OF CONTINUITY (conservation of mass) In complicated patterns of streamline flow, the streamlines effectively define flow tubes. So the equation of continuity – where streamlines crowd together the flow speed must increase.

EQUATION OF CONTINUITY (conservation of mass) m 1 = m 2 V 1 = V 2 A 1 v 1 t = A 2 v 2 t A 1 v 1 = A 2 v 2 A v measures the volume of the fluid that flows past any point of the tube divided by the time interval volume flow rate Q = d. V / dt Q = A v = constant if A decreases then v increases if A increases then v decreases

Applications Rivers Circulatory systems Respiratory systems Air conditioning systems

Blood flowing through our body The radius of the aorta is ~ 10 mm and the blood flowing through it has a speed ~ 300 mm. s-1. A capillary has a radius ~ 4 10 -3 mm but there are literally billions of them. The average speed of blood through the capillaries is ~ 5 10 -4 m. s-1. Calculate the effective cross sectional area of the capillaries and the approximate number of capillaries.

Setup radius of aorta RA = 10 mm = 10 10 -3 m radius of capillaries RC = 4 10 -3 mm = 4 10 -6 m speed of blood thru. aorta v. A = 300 mm. s-1 = 0. 300 m. s-1 speed of blood thru. capillaries RC = 5 10 -4 m. s-1 Assume steady flow of an ideal fluid and apply the equation of continuity Q = A v = constant AA v. A = AC v. C where AA and AC are cross sectional areas of aorta & capillaries respectively. aorta capillaries

Action AC = AA (v. A / v. C) = RA 2 (v. A / v. C) AC = (10 10 -3)2(0. 300 / 5 10 -4) m 2 = 0. 20 m 2 If N is the number of capillaries then A C = N R C 2 N = AC / ( RC 2) = 0. 2 / { (4 10 -6)2} N = 4 109