Teoria podejmowania decyzji Wykad 7 Reduction of compound



























- Slides: 43

Teoria podejmowania decyzji Wykład 7

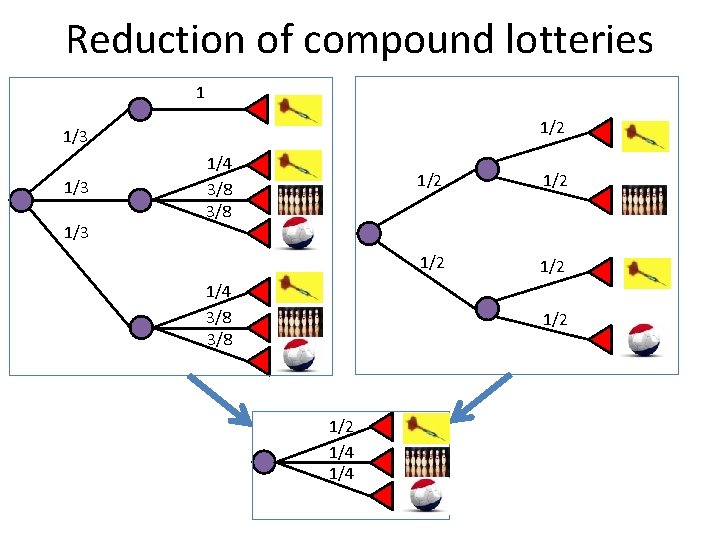
Reduction of compound lotteries 1 A 1/2 1/3 1/3 1/4 3/8 A B 1/2 1/2 A B C 1/4 3/8 A 1/2 B C 1/2 1/4 A B C A C

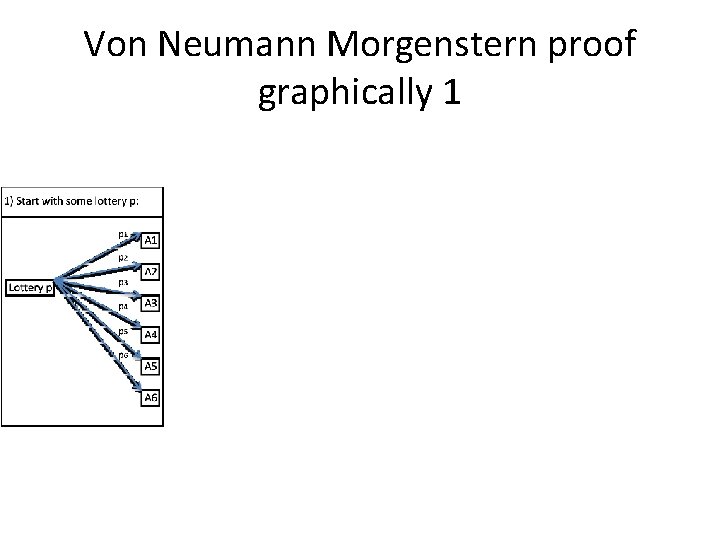
Von Neumann Morgenstern proof graphically 1

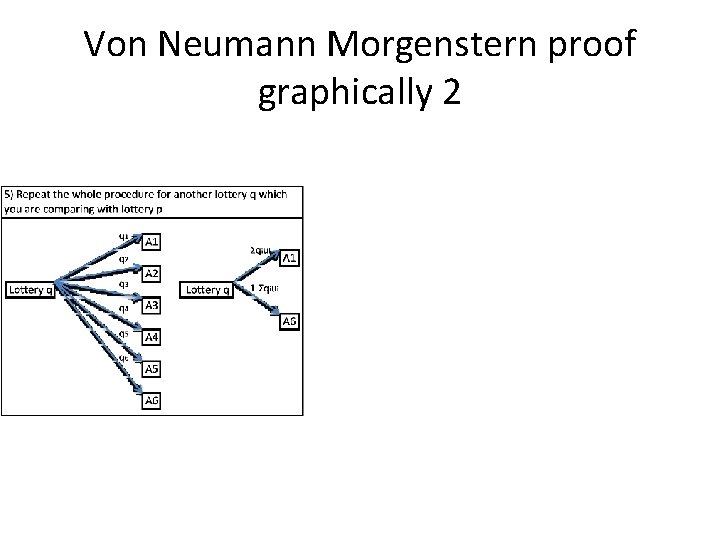
Von Neumann Morgenstern proof graphically 2

Common misunderstandings


Fallacy (2) • Fire insurance: – Fire: pay the premium, house rebuilt (C) – No Fire: pay the premium, house untouched (B) Loss = $70 K Loss = $60 K – Fire: house burnt, no compansation (D) – No Fire: house the same (A) Loss = $100 K Loss = $0 • No insurance: • A≻B≻C≻D • Suppose the probability of fire is 0. 5 • And an individual is indifferent between buying and not buying the insurance • Although Fire insurance has smaller variance and ½u(A) + ½u(D) = ½u(B) + ½u(C), it does not mean that Fire insurance should be chosen over No insurance Risk averse, and EL(insurance) = $65 K EL(no insurance) = $50 K

Fallacy (3) • Fire insurance: – Fire: pay the premium, house rebuilt (C) – No Fire: pay the premium, house untouched (B) • No insurance: – Fire: house burnt, no compansation (D) – No Fire: house the same (A) • A≻B≻C≻D • Suppose that the probability of fire is ½ and an individual prefers not buying fire insurance and hence ½u(A) + ½u(D) > ½u(B) + ½u(C) ⇒ u(A) - u(B) > u(C) - u(D) • However it does not mean that the change from B to A is more preferred than the change from D to C. • Preferences are defined over pairs of alternatives not pairs of alternatives





Crucial axiom - independence • Our version • The general version • Why the general version implies our version?

Independence – examples • If I prefer to go to the movies than to go for a swim, I must prefer: – to toss a coin and: • heads: go to the movies • tails: vacuum clean – than to toss a coin and: • heads: go for a swim • tails: vacuum clean • If I prefer to bet on red than on even in roulette, then I must prefer: – to toss a coin and • heads: bet on 18 • tails: bet on red – than to toss a coin and: • heads: bet on 18 • tails: bet on even 14

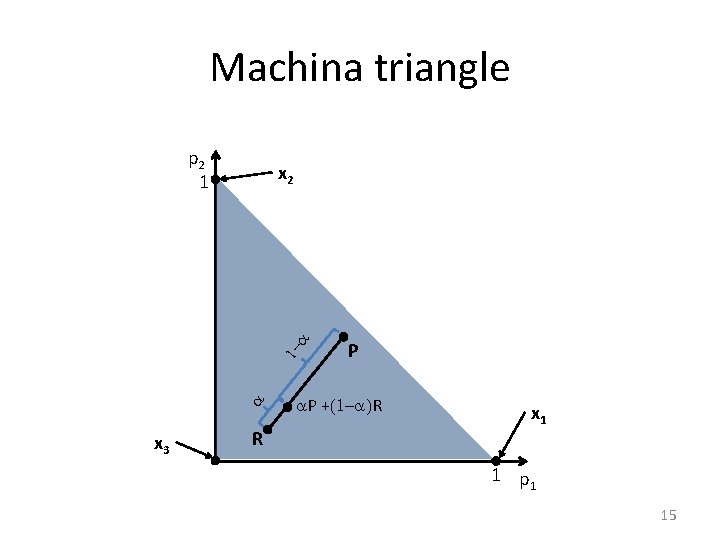
Machina triangle p 2 1 a 1 - a x 2 x 3 R P a. P +(1 -a)R x 1 1 p 1 15

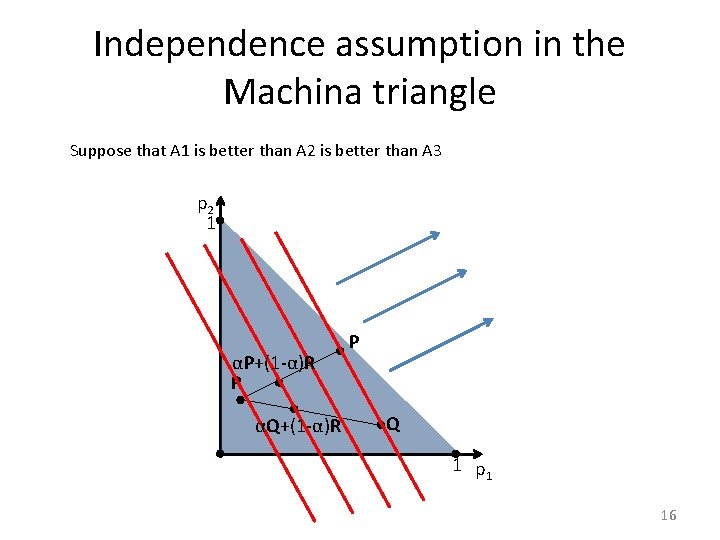
Independence assumption in the Machina triangle Suppose that A 1 is better than A 2 is better than A 3 p 2 1 αP+(1 -α)R R αQ+(1 -α)R P Q 1 p 1 16

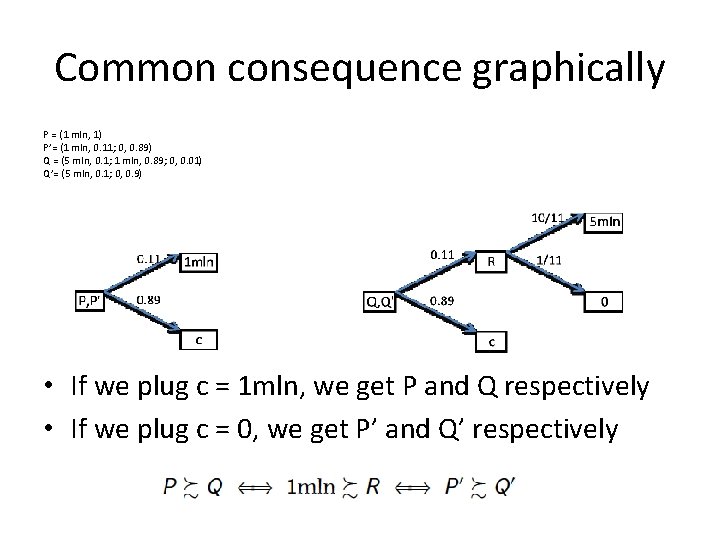
17. 1 and 17. 2 17. 1) Choose one lottery: P=(1 mln, 1) Q=(5 mln, 0. 1; 1 mln, 0. 89; 0 mln, 0. 01) 17. 2) Choose one lottery: P’=(1 mln, 0. 11; 0 mln, 0. 89) Q’=(5 mln, 0. 1; 0 mln, 0. 9) Kahneman, Tversky (1979) [common consequence effect violation of independence] Many people choose P over Q and Q’ over P’

Common consequence graphically P = (1 mln, 1) P’= (1 mln, 0. 11; 0, 0. 89) Q = (5 mln, 0. 1; 1 mln, 0. 89; 0, 0. 01) Q’= (5 mln, 0. 1; 0, 0. 9) • If we plug c = 1 mln, we get P and Q respectively • If we plug c = 0, we get P’ and Q’ respectively

18. 1 i 18. 2 18. 1) Choose one lottery: P=(3000 PLN, 1) Q=(4000 PLN, 0. 8; 0 PLN, 0. 2) 18. 2) Choose one lottery: P’=(3000 PLN, 0. 25; 0 PLN, 0. 75) Q’=(4000 PLN, 0. 2; 0 PLN, 0. 8) Kahneman, Tversky (1979) [common ratio effect, violation of independence] Many people choose P over Q and Q’ over P’

Common ratio graphically P=(3000 PLN, 1) P’=(3000 PLN, 0. 25; 0 PLN, 0. 75) Q=(4000 PLN, 0. 8; 0 PLN, 0. 2) Q’=(4000 PLN, 0. 2; 0 PLN, 0. 8)

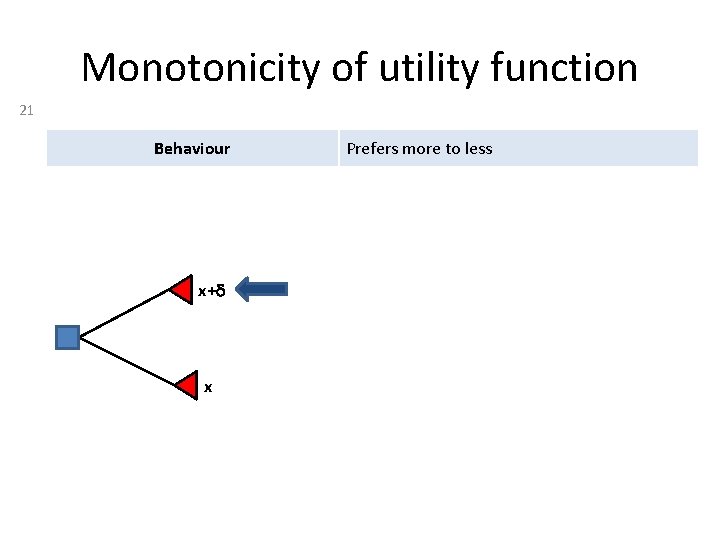
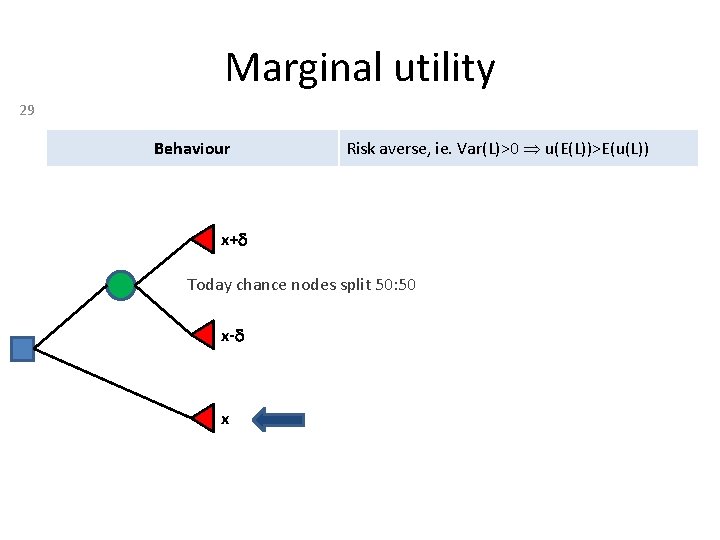
Monotonicity of utility function 21 Behaviour x+d x Prefers more to less

Monotonicity of utility function 22 Behaviour Utility function Prefers more to less x, u’(x)>0; u(x) – increasing

Monotonicity of utility function 23 Behaviour Utility function Prefers more to less x, u’(x)>0; u(x) – increasing Attitude towards risk (quantitatively) u(x)/u’(x) – fear of ruin • prefers more to less • current wealth x • probability p of bankruptcy (u(0)=0) • how much to pay to avoid it?

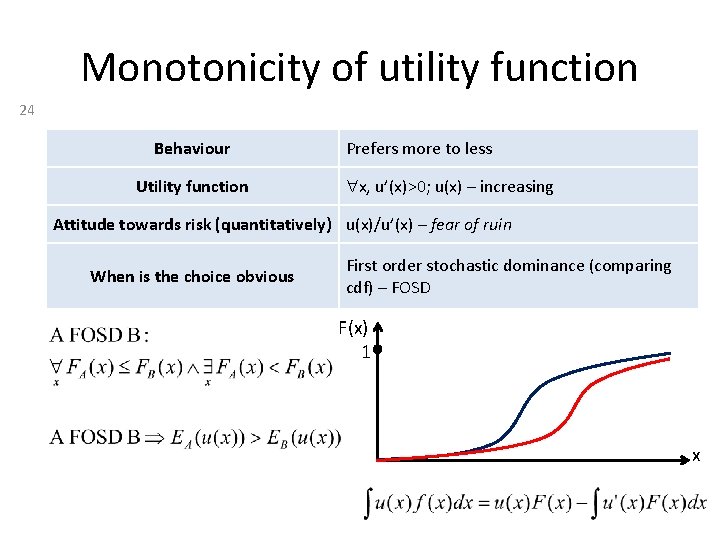
Monotonicity of utility function 24 Behaviour Utility function Prefers more to less x, u’(x)>0; u(x) – increasing Attitude towards risk (quantitatively) u(x)/u’(x) – fear of ruin When is the choice obvious First order stochastic dominance (comparing cdf) – FOSD F(x) 1 x

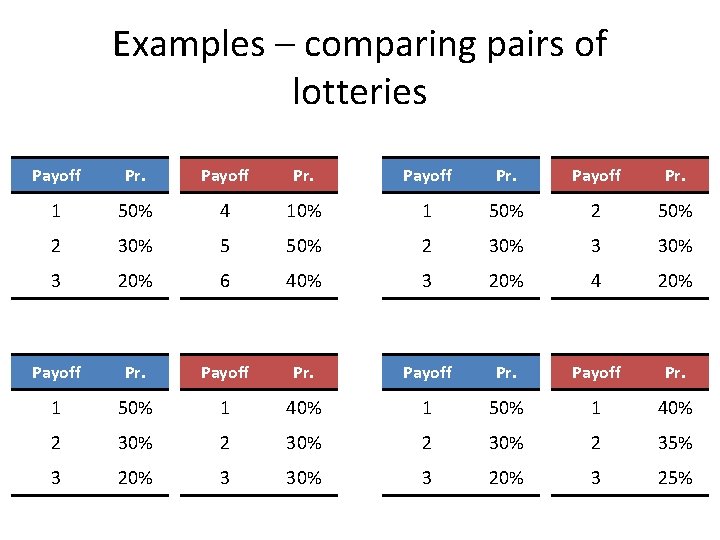
Examples – comparing pairs of lotteries Payoff Pr. 1 50% 4 10% 1 50% 2 30% 5 50% 2 30% 3 20% 6 40% 3 20% 4 20% Payoff Pr. 1 50% 1 40% 2 30% 2 35% 3 20% 3 30% 3 25%

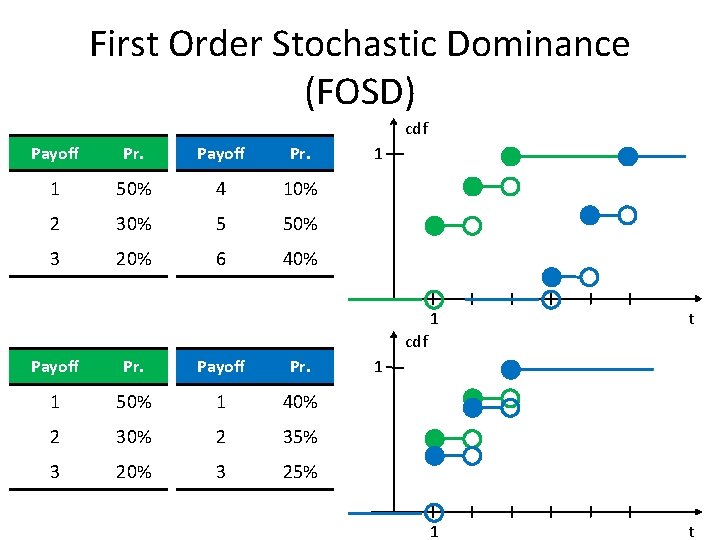
First Order Stochastic Dominance (FOSD) cdf Payoff Pr. 1 50% 4 10% 2 30% 5 50% 3 20% 6 40% 1 1 t cdf Payoff Pr. 1 50% 1 40% 2 35% 3 20% 3 25% 1

FOSD • Assume X and Y are two different lotteries (FX(. ), FY(. ) are not the same) • Lottery X FOSD Y if: For all a, hence: Those who prefer more to less will never choose lottery that is dominated in the above sense. • Theorem: X FOSD Y if and only if Eu(X) ≥ Eu(Y), for all inreasing u

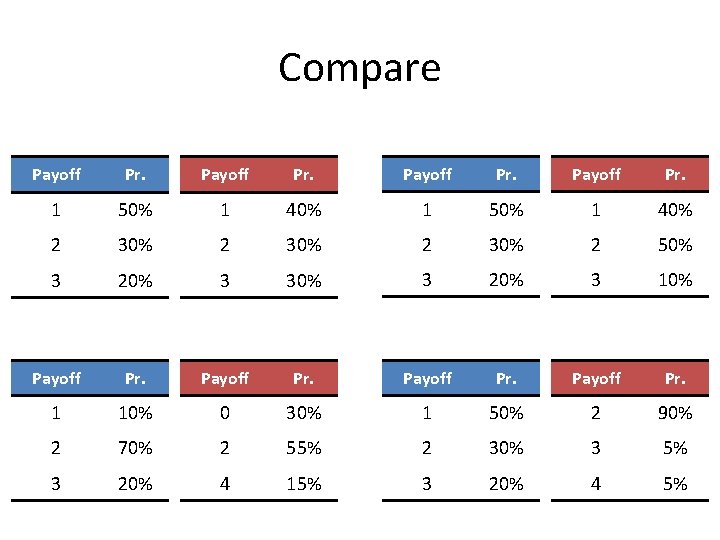
Compare Payoff Pr. 1 50% 1 40% 2 30% 2 50% 3 20% 3 30% 3 20% 3 10% Payoff Pr. 1 10% 0 30% 1 50% 2 90% 2 70% 2 55% 2 30% 3 5% 3 20% 4 15% 3 20% 4 5%

Marginal utility 29 Behaviour Risk averse, ie. Var(L)>0 u(E(L))>E(u(L)) x+d Today chance nodes split 50: 50 x-d x

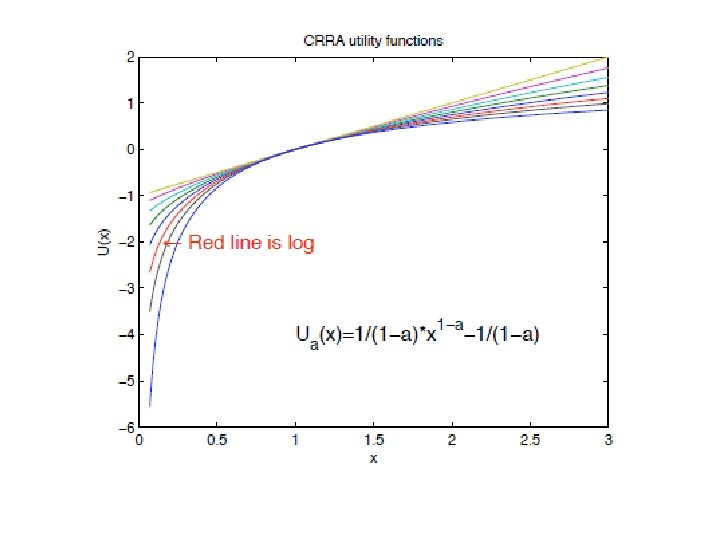
Marginal utility 30 Behaviour utility Utility function payoff Risk averse, ie. Var(L)>0 u(E(L))>E(u(L)) x, u’(x)>0, u’’(x)<0; u(x) – concave, increasing

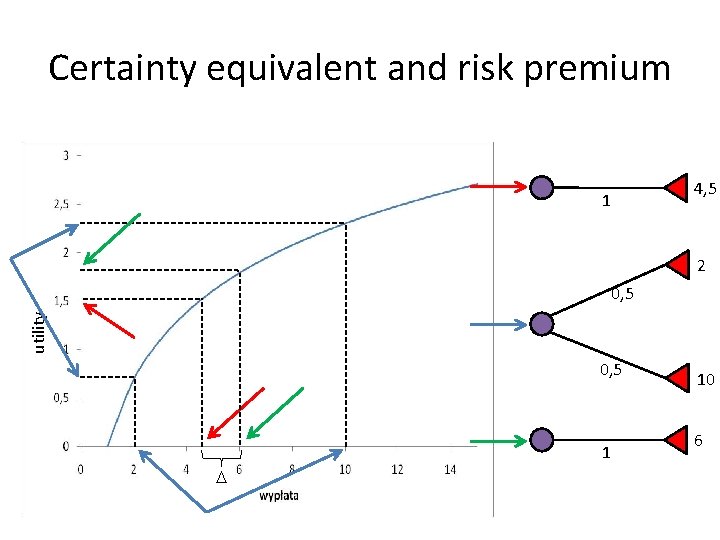
Certainty equivalent and risk premium 1 4, 5 2 utility 0, 5 1 10 6

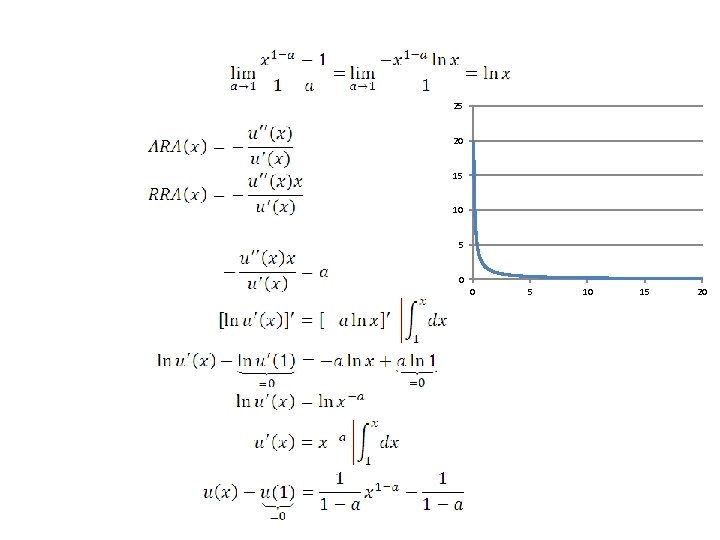
Marginal utility 32 Behaviour Utility function Risk averse, ie. Var(L)>0 u(E(L))>E(u(L)) x, u’(x)>0, u’’(x)<0; u(x) – concave, increasing Attitude towards risk (quantitatively) -u’’(x)/u’(x) – Arrow-Pratt risk aversion coeff. • • • x – initial wealth (number) l – lottery with zero exp. value (random variable) k – multiplier (we tak k close to zero) d – risk premium (number) x-d – certainty equivalent for x+l

Marginal utility 33 Behaviour Utility function Risk averse, ie. Var(L)>0 u(E(L))>E(u(L)) x, u’(x)>0, u’’(x)<0; u(x) – concave, increasing Attitude towards risk (quantitatively) -u’’(x)/u’(x) – Arrow-Pratt risk aversion coeff. When is the choice obvious Second order stochastic dominance (integrals of cdf) – SOSD

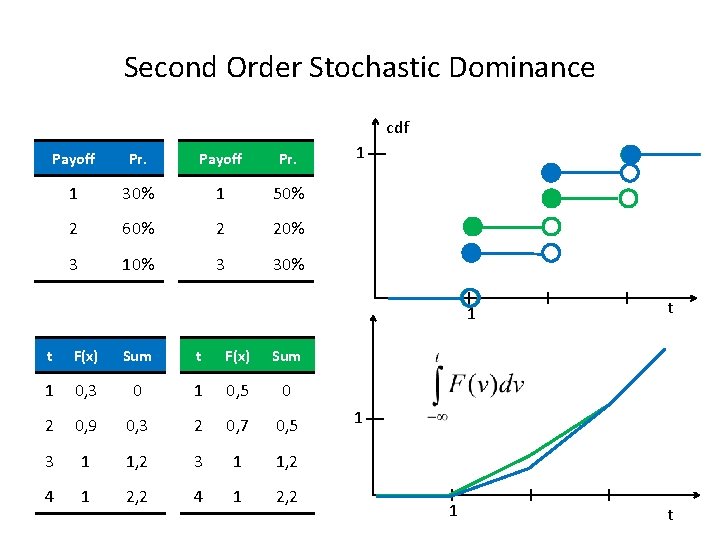
Second Order Stochastic Dominance cdf Payoff Pr. 1 30% 1 50% 2 60% 2 20% 3 10% 3 30% 1 1 t F(x) Sum 1 0, 3 0 1 0, 5 0 2 0, 9 0, 3 2 0, 7 0, 5 3 1 1, 2 4 1 2, 2 t 1 1 t

SOSD • Assume X and Y are two different lotteries (FX(. ), FY(. ) are not the same) • Lottery X SOSD Y if: For all a hence: • Those who are risk averse will never choose a lottery that is dominated in the above sense. • Theorem: X SOSD Y if and only if Eu(X) ≥ Eu(Y), for all inreasing and concave u

Compare and find FOSD and SOSD Payoff Pr. 1 50% 1 60% 1 15% 1 20% 2 30% 2 10% 2 45% 2 40% 3 20% 3 30% 3 40% Payoff Pr. 1 10% 1 30% 1 40% 2 50% 2 15% 2 40% 2 15% 3 40% 3 55% 3 30% 3 45%

Mean-variance criterium • Risk aversion doesn’t mean that always: A better than B, if only E(A)=E(B) and Var(A)<Var(B) – some lotteries do not result from another with mean preserving spread – is true when Var(A)=0 • Mean-variance criterium works e. g. for normally distributed random variables (lotteries) Lottery X Lottery Y Prob. x u(x)=ln(x) (x-EX)2 y u(y)=ln(y) (y-EY)2 20% 20, 1 3 65, 61 4 1, 386 64 80% 9, 975 2, 3 4, 1 14 2, 639 4 mean 12 2, 44 16, 4 12 2, 388 16 37

Measures of risk aversion • Risk premium measures risk aversion with respect to a given lottery • As a function of payoff values risk aversion is measured by Arrow, Pratt measures of (local) risk aversion


25 20 15 10 5 0 0 5 10 15 20

Exercise 1 • From now on let’s assume X is a set of monetary payoffs (decision maker prefers more money than less) • Decision maker with v. NM utility function prefers lottery (100, ¼; 1000, ¾) to (500, ½; 1000, ½) • What is a realtion between (100, ½; 500, ¼; 1000, ¼) and (100, ¼; 500, ¾)? • Suggestion – we can arbitrarily set utility function for two outcomes 41

Exercise 2 • Decision maker is indifferent between pairs of lotteries: (500, 1) and (0, 0, 4; 1000, 0, 6) and (300, 1) and (0, ½; 500, ½) • Can we guess the preference relation between (0, 0, 2; 300, 0, 3; 1000, ½) and (500, 1)? 42

Exercise 3 • Decision maker with v. NM utility is risk averse and indifferent between the following pairs (400, 1) and (0, 0, 3; 1000, 0, 7) and (0, ½; 200, ½) and (0, 5/7; 400, 2/7) • Can we guess the preference relation between (200, ½; 600, ½) and (0, 4/9; 100, 5/9)? • (suggestion – remamber than v. NM utility is concave) 43
 Wady i zalety grupowego podejmowania decyzji
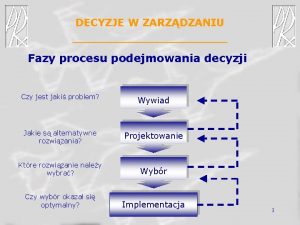
Wady i zalety grupowego podejmowania decyzji Fazy procesu podejmowania decyzji
Fazy procesu podejmowania decyzji Zasada trwałości decyzji ostatecznych
Zasada trwałości decyzji ostatecznych Typy decyzji
Typy decyzji Elementy decyzji administracyjnej
Elementy decyzji administracyjnej Przeniesienie decyzji o środowiskowych uwarunkowaniach
Przeniesienie decyzji o środowiskowych uwarunkowaniach Decyzja administracyjna
Decyzja administracyjna Rodzaje decyzji administracyjnych
Rodzaje decyzji administracyjnych Zasada trwałości decyzji ostatecznych
Zasada trwałości decyzji ostatecznych System wspomagania decyzji wop
System wspomagania decyzji wop So3h
So3h Simple compound complex rules
Simple compound complex rules A compound differs from an element in that a compound
A compound differs from an element in that a compound Simple and compound subjects and predicates
Simple and compound subjects and predicates Pauline and bruno have a big argument
Pauline and bruno have a big argument A compound differs from an element in that a compound
A compound differs from an element in that a compound Compound predicate
Compound predicate Cost reduction strategies
Cost reduction strategies Bevel epicyclic gear train
Bevel epicyclic gear train Contraindications of all ceramic crowns
Contraindications of all ceramic crowns Wsjf values
Wsjf values Self oxidation reduction reaction of aldehyde
Self oxidation reduction reaction of aldehyde Subset sum 3sat reduction
Subset sum 3sat reduction What is reduction
What is reduction Nursemaid elbow reduction cpt
Nursemaid elbow reduction cpt Functional group of acyl chloride
Functional group of acyl chloride Nlp dimensionality reduction
Nlp dimensionality reduction Ackermann reduction
Ackermann reduction Size reduction
Size reduction Trrp guidance
Trrp guidance Clinical variation reduction
Clinical variation reduction Chlorination of benzene
Chlorination of benzene Vaser lipo dubai
Vaser lipo dubai Changing adjective clause to adjective phrase
Changing adjective clause to adjective phrase Poverty reduction workgroup
Poverty reduction workgroup Instrumentation amplifier noise reduction
Instrumentation amplifier noise reduction Reduction of vat dyes
Reduction of vat dyes Drive reduction theory
Drive reduction theory Oxidation–reduction reactions
Oxidation–reduction reactions Reduction formula
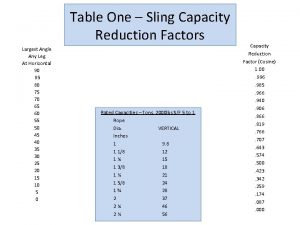
Reduction formula Sling angle reduction factor
Sling angle reduction factor Which is the type of motion of size separation?
Which is the type of motion of size separation? Dhamma
Dhamma Boolean algebra reduction
Boolean algebra reduction