Tema Algoritam razgranate strukture na primeru kvadratne jednaine

Tema: Algoritam razgranate strukture na primeru kvadratne jednačine Jasmina Milić

Algoritam se definiše kao konačan, uređen niz precizno formulisanih pravila kojima se rešava jedan ili čitava klasa problema. Algoritam proizvoljne složenosti može biti predstavljen kombinacijom tri bazne strukture: linijske, razgranate i ciklične.

• Linijskim se nazivaju algoritmi kod kojih se naredbe (ili instrukcije) izvršavaju jedna za drugom-svaka naredba izvršava se tačno jedanput. • Razgranatim se nazivaju algoritmi kod kojih se u zavisnosti od vrednosti logičkog uslova izvršavanje nastavlja jednom od dve grane-svaka naredba izvršava se najviše jedanput. • Cikličnim se nazivaju algoritmi koji sadrže niz instrukcija (telo ciklusa) koje se mogu ponavljati više puta.

• Postupak građenja algoritma razgranate strukture ilustrovaćemo na primeru kvadratne jednačine. • Formulaciju rešiti kvadratnu jednačinu ax 2+bx+c=0 možemo smatrati postavkom problema. • Da bi rešili ovaj problem treba da odgovorimo na sledeća pitanja: – Koje su veličine poznate (ili ulazne), a koje su nepoznate (ili izlazne) ? – Koje su moguće veze između poznatih i nepoznatih veličina? – Šta se izdaje kao rezultat?

Za dati problem na postavljena pitanja mogu se dati sledeći odgovori: – Ulazne veličine su koeficijenti kvadratne jednačine a, b i c - Veze imeđu poznatih i nepoznatih veličina uspostavljamo odgovarajućom diskusijom - Izlazne veličine su rešenja kvadratne jednačine x 1, x 2 ili odgovarajući komentar

Diskusija se svodi na razmatranje sledeća dva slučaja: 1. a≠ 0 - potpuna kvadratna jednačina 2. a=0 –jednačina nije kvadratna

a≠ 0, potpuna kvadratna jednačina računamo diskriminantu D=b 2 -4 ac i razmatramo slučajeve D>0 D=0 rešenja su realna i različita i jednaka D<0 rešenja su konjugovanokomleksna

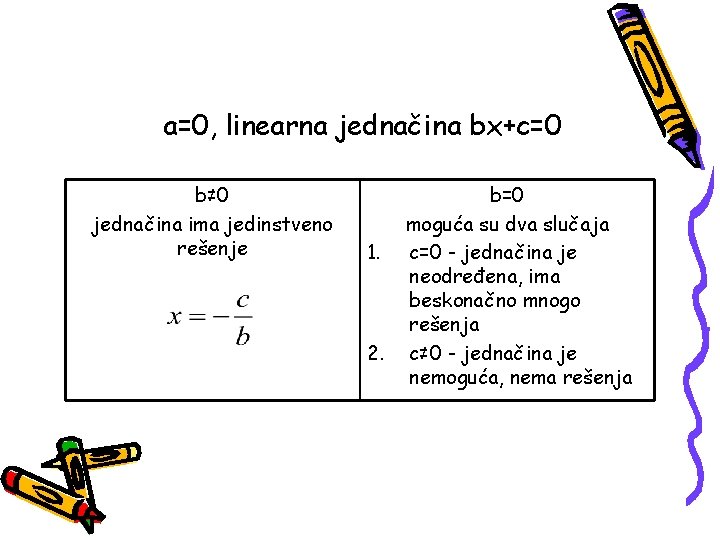
a=0, linearna jednačina bx+c=0 b≠ 0 jednačina ima jedinstveno rešenje 1. 2. b=0 moguća su dva slučaja c=0 - jednačina je neodređena, ima beskonačno mnogo rešenja c≠ 0 - jednačina je nemoguća, nema rešenja

Sada se algoritam može izraziti tekstualnim opisom: Korak 1. Definisati vrednosti ulaznih veličina: a, b i c Korak 2. Pitati da li je a≠ 0 DA: 1. Izračunati vrednost diskriminante D=b 2 -4 a*c 2. Pitati da li je D>0 DA: 1. Izračunati x 1=(-b+D 1/2)/(2*a) 2. Izračunati x 2=(-b-D 1/2)/(2*a) 3. Definisati rezultate, realna i različita rešenja x 1 i x 2 NE: 1. Pitati da li je D=0 DA: 1. Izračunati x=-b/(2*a) 2. Definisati dvostruko rešenje x 1=x 2=x NE: 1. Izračunati Re=-b/(2*a) 2. Izračunati Im=(-D)1/2/(2*a) 3. Definisati konjugovano kompleksna rešenja x 1=Re+i*Im i x 2=Re-i*Im NE: 1. Pitati da li je b≠ 0 DA: 1. Izračunati x=-c/b 2. Definisati x- jedinstveno rešenje linearne jednačine NE: 1. Pitati da li je c=0 DA: 1. Izdati komentar da je jednačina neodređena NE: 1. Izdati komentar da je jednačinna nemoguća

• Ovo je primer algoritma na prirodnom jeziku. • Algoritam opisuje operacije ne nad konkretnim vrednostima, već nad apstraktnim objektima (njegova formulacija ne zavisi od vrednosti promenljivih a, b i c). • Samim tim isti algoritam može se primeniti za rešavanje bilo koje kvadratne jednačine. • Kako je tekstualni opis algoritma kod složenijih problema teško čitljiv, pribegava se preglednijem grafičkom prikazu algoritma. • Grafički prikaz algoritma se naziva blok šema ili algoritamska šema.

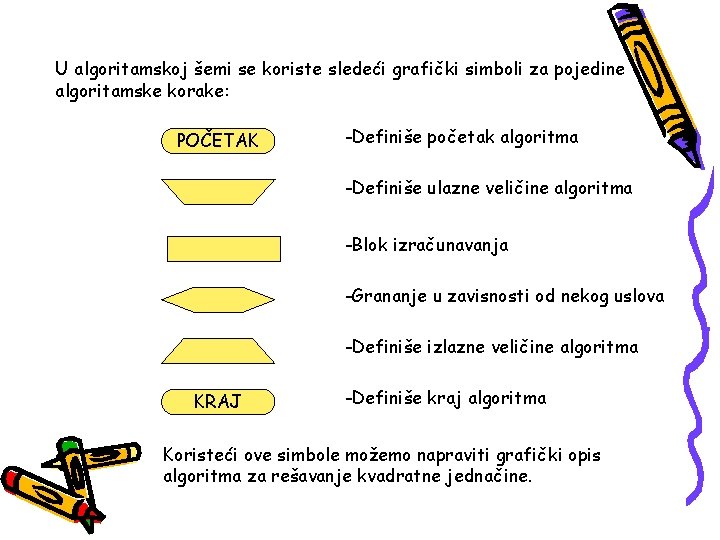
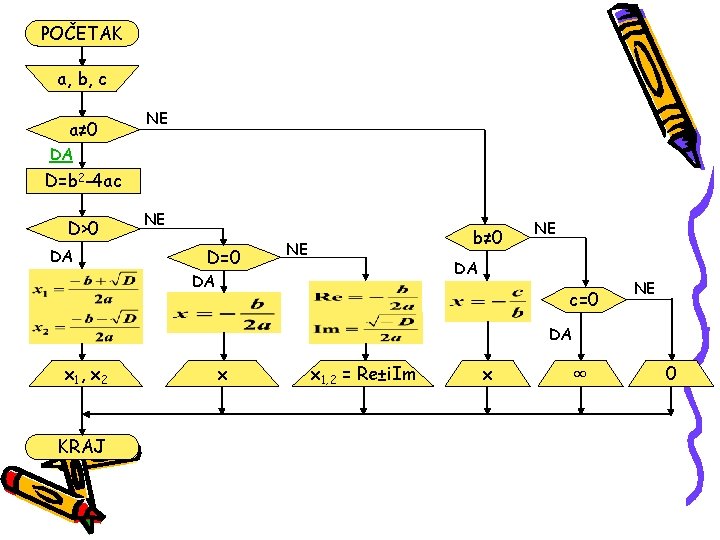
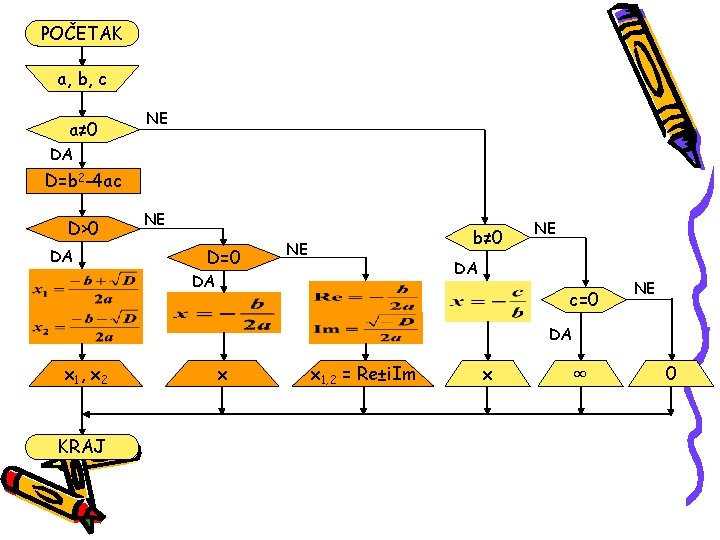
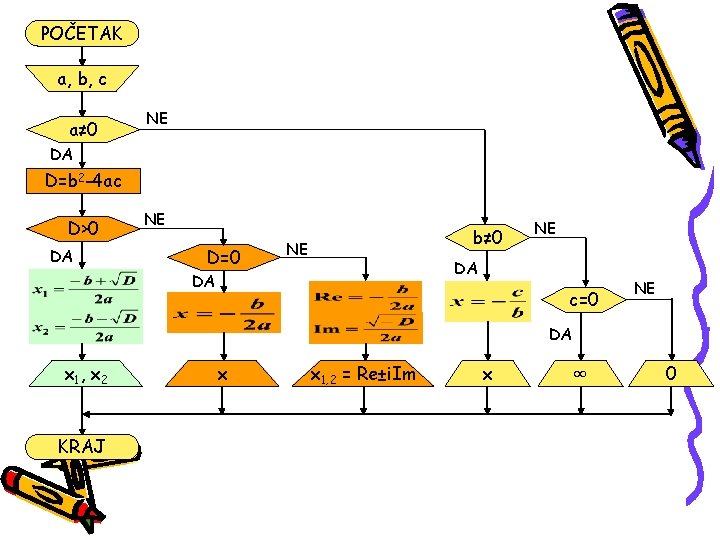
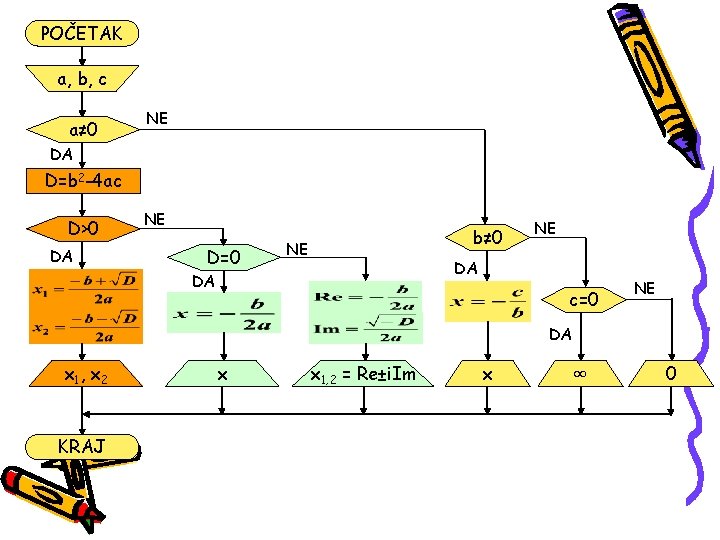
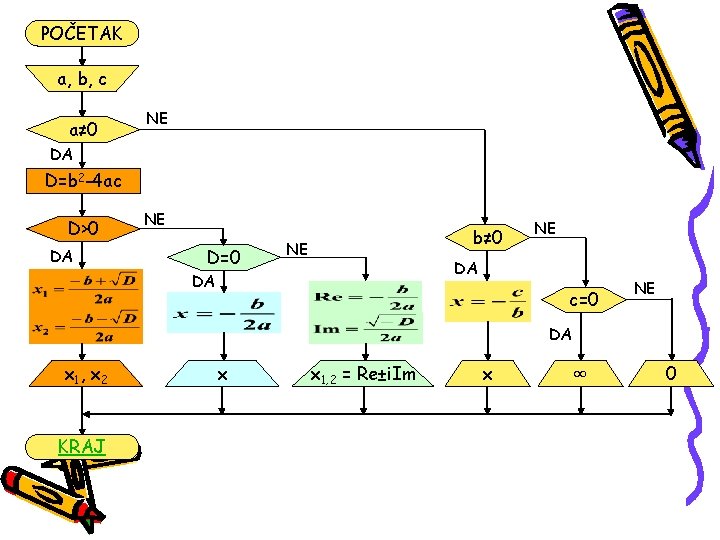
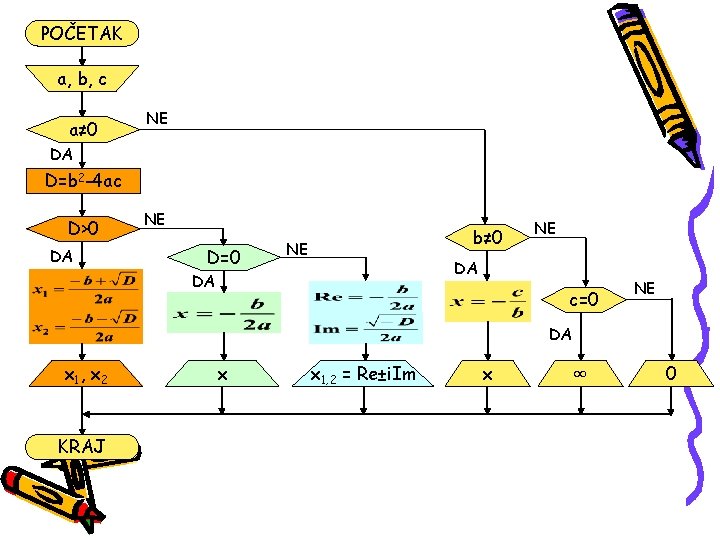
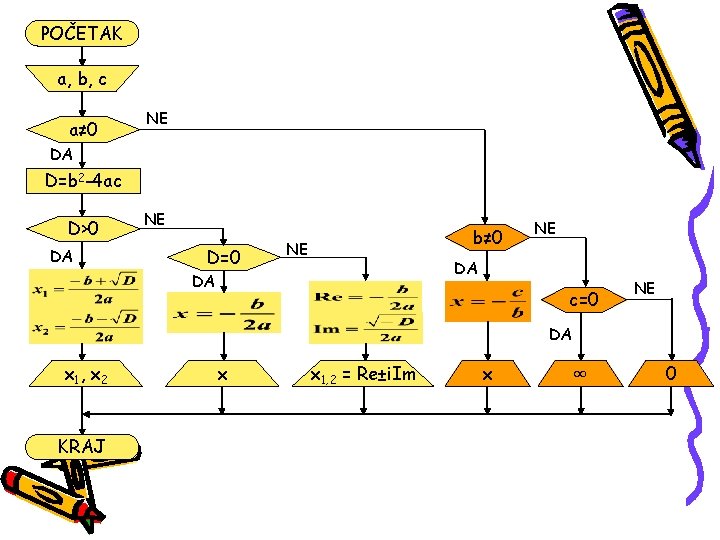
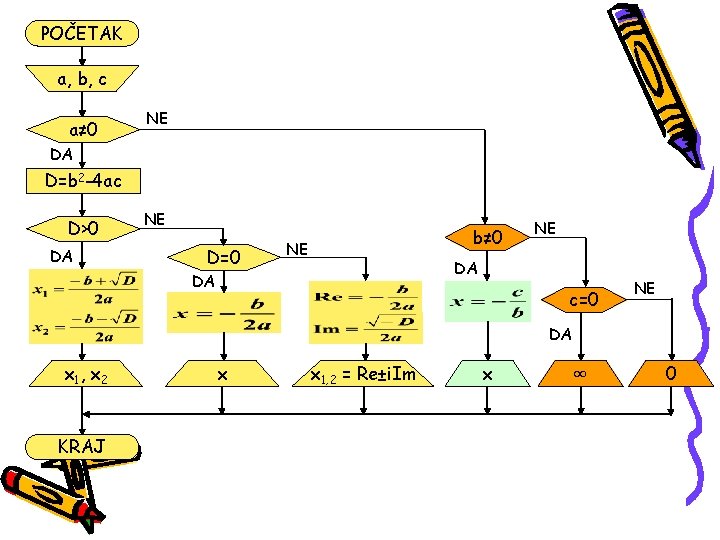
U algoritamskoj šemi se koriste sledeći grafički simboli za pojedine algoritamske korake: POČETAK -Definiše početak algoritma -Definiše ulazne veličine algoritma -Blok izračunavanja -Grananje u zavisnosti od nekog uslova -Definiše izlazne veličine algoritma KRAJ -Definiše kraj algoritma Koristeći ove simbole možemo napraviti grafički opis algoritma za rešavanje kvadratne jednačine.

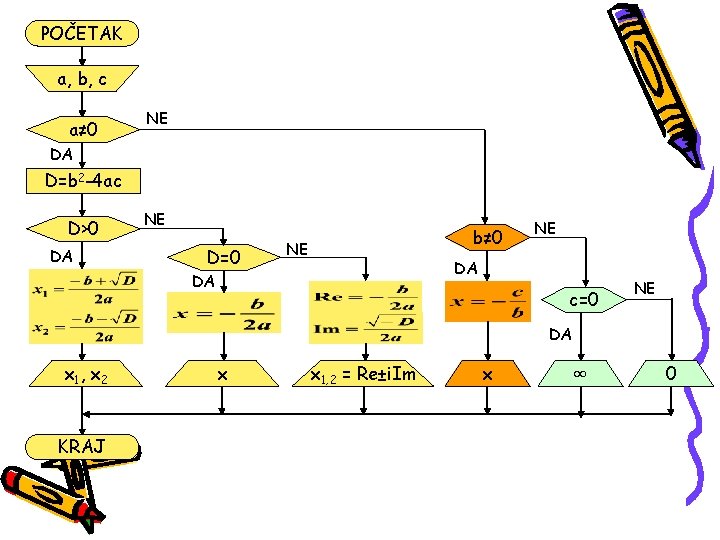
POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

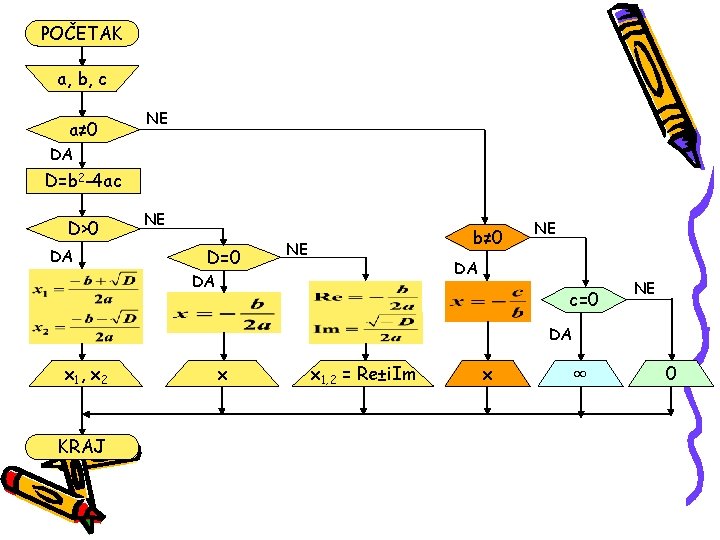
POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

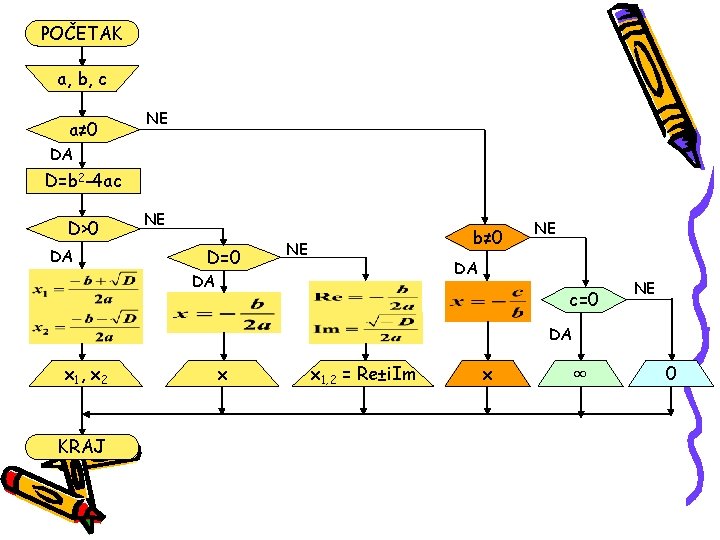
POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

POČETAK a, b, c a≠ 0 NE DA D=b 2 -4 ac D>0 DA NE D=0 b≠ 0 NE NE DA DA c=0 NE DA x 1 , x 2 KRAJ x x 1, 2 = Re±i. Im x ∞ 0

Algoritam je dobar ukoliko ispunjava sledeće zahteve: 1. Definisanost-svaka naredba algoritma je jednoznačno definisana, nema proizvoljnih i nejasnih tumačenja 2. Determinisanost-vrednosti koje se dobijaju u bilo kom koraku jednoznačno su određene vrednostima iz prethodnih koraka 3. Izvršivost-svaka naredba je izvršiva; primer neizvršive naredbe bio bi: “Promenljivoj X dodeliti najveći realan broj manji od 1. ” 4. Masovnost-algoritam rešava opštu klasu problema, koji se razlikuju samo po ulaznim veličinama. Na primer, umesto kreiranja algoritma koji rešava jednačinu x 2 -2 x+1=0 rešen je opšti slučaj ax 2+bx+c=0 5. Rezultativnost-algoritam u konačnom nizu koraka daje tražene rezultate za sve slučajeve za koje je kreiran

Jednostavnom proverom možemo utvrditi da naš algoritam ispunjava sve navedene zahteve. Vežbe radi zapisaćemo algoritme za rešavanje sledećih problema: 1. 2. 3. 4. Odrediti min (max) brojeva a i b. Odrediti min (max) brojeva a, b i c. Ukoliko je a>b (a<b), zameniti mesta promenljivima a i b. Za date vrednosti x i y izračunati z po formuli: 5. Za dato x izračunati y po formuli:

Domaći zadatak: • Zapisati algoritam kojim se rešava sistem od dve linearne jednačine sa dve nepoznate: a 1 x+b 1 y=c 1 a 2 x+b 2 y=c 2. • Ako se od odsečaka sa dužinama x, y i z može konstruisati trougao, izračunati njegovu površinu po formuli:

K R A J