Strukture podataka i algoritmi 13 TEINSKI GRAFOVI Teinski






























- Slides: 50

Strukture podataka i algoritmi 13. TEŽINSKI GRAFOVI

Težinski grafovi • Osnovni pojmovi i definicije • Minimalno povezujuće stablo • Kruskalov algoritam • Primov algoritam • Najkraći putevi od jednog čvora • Dijkstrin algoritam • Najkraći putevi između svih čvorova • Flojdov algoritam Strukture podataka i algoritmi

Težinski grafovi • • • Prirodan model za predstavljanje problema gdje sve grane grafa nisu ravnopravne već neke imaju veću „težinu“. Primjeri: računari kao čvorovi i komunikacioni linkovi između njih kao grane. Težinski grafovi su grafovi čijim granama je dodjeljena neka numerička vrijednost tzv. težina. Strukture podataka i algoritmi

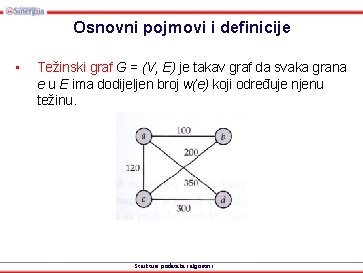
Osnovni pojmovi i definicije • Težinski graf G = (V, E) je takav graf da svaka grana e u E ima dodijeljen broj w(e) koji određuje njenu težinu. Strukture podataka i algoritmi

Osnovni pojmovi i definicije • Običan graf se može smatrati težinskim čije su sve grane jednake (težine 1). • I težinski grafovi se mogu predstaviti pomoću matrice susjedstva i pomoću liste susjedstva. Strukture podataka i algoritmi

Matrica susjedstva za težinski graf • • Postojanje neke grane e i njena težina w(e) zajedno se predstavljaju odgovarajućim elementom matrice w(e). Ako neka grana ne postoji u grafu odgovarajući element matrice susjedstva mora biti neka vrijednost koja nije moguća za grane (∞). Strukture podataka i algoritmi

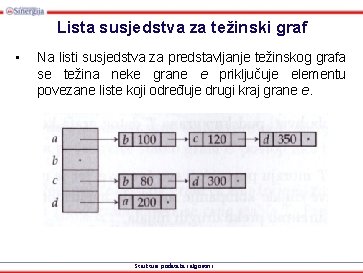
Lista susjedstva za težinski graf • Na listi susjedstva za predstavljanje težinskog grafa se težina neke grane e priključuje elementu povezane liste koji određuje drugi kraj grane e. Strukture podataka i algoritmi

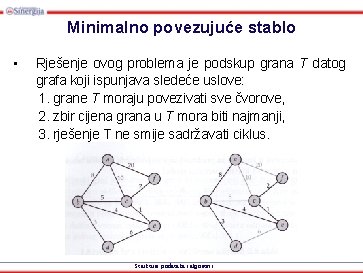
Minimalno povezujuće stablo • Primjer: graf sa čvorovima koji predstavljaju filijale neke kompanije u različitim gradovima. • Grane sa numeričkim vrijednostima neka predstavljaju cijene iznajmljivanja telekomunikacionih linija između filijala. • Problem: odrediti najmanju cijenu iznajmljivanja telekomunikacionih linija između filijala. Strukture podataka i algoritmi

Minimalno povezujuće stablo • Rješenje ovog problema je podskup grana T datog grafa koji ispunjava sledeće uslove: 1. grane T moraju povezivati sve čvorove, 2. zbir cijena grana u T mora biti najmanji, 3. rješenje T ne smije sadržavati ciklus. Strukture podataka i algoritmi

Minimalno povezujuće stablo • Minimalno povezujuće stablo T težinskog grafa G = (V, E) je podgraf (V, T) grafa G čiji je zbir težina grana minimalan. • U slučaju povezanog težinskog grafa G, zbir težina grana u nekom povezujućem stablu T tog grafa se naziva cijena stabla T. Strukture podataka i algoritmi

Minimalno povezujuće stablo • Graf G može imati veliki broj povezujućih stabala čija struktura je potpuno različita. • Algoritmi za određivanje minimalnog povezujućeg stabla: - Kruskalov algoritam, - Primov algoritam. • Ovi algoritmi se zasnivaju na svojstvu podjele grafa. Strukture podataka i algoritmi

Svojstvo podjele grafa • • Neka je G = (V, E) povezan težinski graf i neka su V 1 i V 2 dva neprazna disjunktna podskupa njegovog skupa čvorova V takva da je V = V 1 U V 2. Ako je e jedinstvena grana najmanje težine u E takva da joj je jedan kraj u V 1 i drugi kraj u V 2, onda svako minimalno povezujuće stablo grafa G sadrži granu e. Strukture podataka i algoritmi

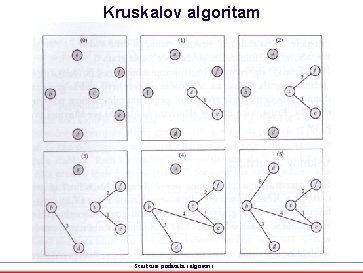
Kruskalov algoritam • • Radi konstruisanja minimalnog povezujućeg stabla težinskog grafa G = (V, E) polazi se od šume (V, 0) koja se sastoji od svih čvorova grafa G i nema nijednu granu. Redom se ispituju grane grafa u rastućem redoslijedu njihovih težina. Ako grana e povezuje dva čvora iz dva različita stabla do tada konstruisane šume onda se e dodaje skupu izabranih grana i ta dva stabla se objedinjuju u jedno stablo. Ako e povezuje dva čvora iz istog stabla onda se e odbacuje jer bi proizvela ciklus. Strukture podataka i algoritmi

Kruskalov algoritam Strukture podataka i algoritmi

Implementacija Kruskalovog algoritma • • Obrazovati običan niz od grana G sa pridruženim težinama. Sortirati taj niz u rastućem redoslijedu po težinama grana i neka je e[1], e[2], . . . , e[m] dobijeni niz sortiranih grana. Strukture podataka i algoritmi

Kruskalov algoritam // Ulaz: povezan težinski graf G // Izlaz: minimalno povezujuće stablo T grafa G algorithm mst-kruskal(G) T = 0; // šuma T je početno stablo bez grana // svi čvorovi su stabla šume T for (svaki čvor v u grafu G) do ds-make(v); // od svakog čvora se formira po jedno stablo for i = 1 to m do e[i] = {u, v}; a = ds-find(u); // ime skupa kome pripada čvor u b = ds-find(v); // ime skupa kome pripada čvor v if (a != b) then // skupovi čvorova u i v nisu isti T = T + e[i]; // dodati granu ei šumi T ds-union(a, b); // objediniti skupove čvorova u i v return T; Strukture podataka i algoritmi

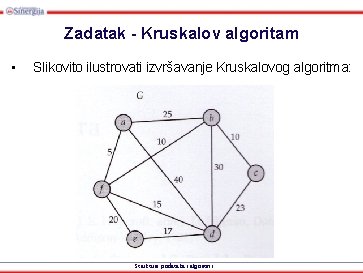
Zadatak - Kruskalov algoritam • Slikovito ilustrovati izvršavanje Kruskalovog algoritma: Strukture podataka i algoritmi

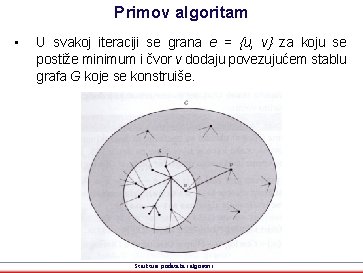
Primov algoritam • Minimalno povezujuće stablo se dobija tako što se početno najprostije stablo postupno proširuje. • Početno stablo je neki proizvoljno izabran čvor s. • U svakom koraku se djelimično konstruisanom stablu dodaje novi čvor na drugom kraju grane najmanje težine koja izlazi iz stabla. Strukture podataka i algoritmi

Primov algoritam • U svakoj iteraciji se grana e = {u, v} za koju se postiže minimum i čvor v dodaju povezujućem stablu grafa G koje se konstruiše. Strukture podataka i algoritmi

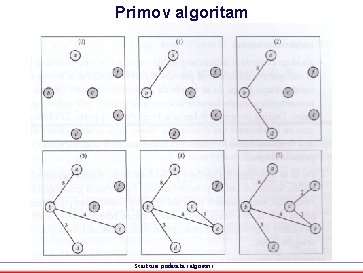
Primov algoritam Strukture podataka i algoritmi

Implementacija Primovog algoritma • • • Da bi se efikasno realizovao Primov algoritam mora se pažljivo voditi evidencija o skupu čvorova S i skupu grana T koji pripadaju djelimično konstruisanom povezujućem stablu grafa G. Grane čiji je samo jedan kraj u skupu S moraju se organizovati tako da se od njih može brzo izabrati jedna grana minimalne težine. Da bi se brzo odredila sledeća grana koju treba dodati djelimičnom stablu koristi se red sa prioritetima čiji elementi su grane grafa G pri čemu jedno polje sadrži granu e = {u, v} a drugo polje njenu težinu w(e). Strukture podataka i algoritmi

Primov algoritam // Ulaz: povezan težinski graf G // Izlaz: minimalno povezujuće stablo T grafa G algorithm mst-prim(G) Proizvoljno izabrati čvor s u G; S = {s}; T = 0; // inicijalizovati djelimično stablo q = 0; // konstruisati prazan red sa prioritetima for (svaka grana e={s, x} u grafu G) do pq-insert(q, (w(e), e)); // u red sa prioritetima dodati granu while (q != 0) do e = pq-deletemin(q); // u redu se pronalazi najmanja grana Neka je e = {u, v}; T = T + e; // granu e dodati granama delimičnog stabla S = S + v; // drugi kraj v dodati čvorovima tog stabla for (svaka grana e={v, x} za koju x nije u S) do pq-insert(q, (w(e), e)); return T; Strukture podataka i algoritmi

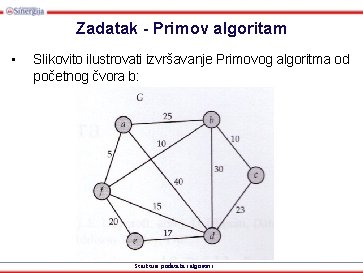
Zadatak - Primov algoritam • Slikovito ilustrovati izvršavanje Primovog algoritma od početnog čvora b: Strukture podataka i algoritmi

Najkraći putevi od jednog čvora • • Svaka grana u težinskom grafu G ima pridruženu dužinu l(e) ≥ 0 koja predstavlja mjeru prelaska u jednom koraku od čvora u do čvora v. Za neki put P u grafu G, dužina tog puta l(P) je zbir dužina svih grana na putu P. Problem najkraćih puteva od jednog čvora sastoji se u tome da se za dati čvor s u težinskom grafu G odrede najkraći putevi od tog čvora s do svih ostalih čvorova u grafu G. Za rješenje ovog problema se koristi Dijkstrin algoritam. Strukture podataka i algoritmi

Dijkstrin algoritam • Problem nalaženja najkraćih puteva od jednog čvora se rješava pretragom u širinu. • Najkraći putevi od datog čvora s do ostalih čvorova se otkrivaju u rastućem redoslijedu dužina najkraćih puteva. • U algoritmu se postupno konstruiše skup čvorova S takav da je za svaki čvor u u S određena dužina najkraćeg puta d(u) od čvora s. • To je skup riješenih čvorova grafa G. Strukture podataka i algoritmi

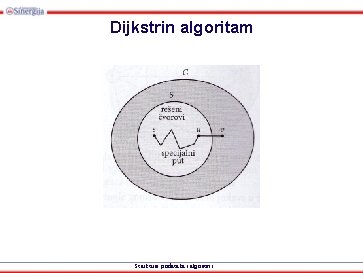
Dijkstrin algoritam • Na početku je S = {s} i d(s) = 0. • Da bi se u narednoj iteraciji skup riješenih čvorova S proširio za jedan čvor, za svaki neriješen čvor u u V-S se određuje dužina najkraćeg specijalnog puta od s do v. • Specijalni put do čvora v je neki put koji počinje od čvora s, zatim prolazi samo kroz riješene čvorove i na kraju dolazi do nekog čvora u iz S i završava se jednom granom u čvoru v. Strukture podataka i algoritmi

Dijkstrin algoritam Strukture podataka i algoritmi

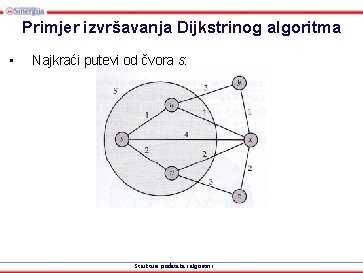
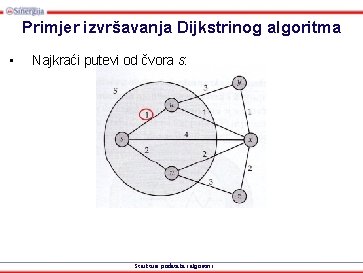
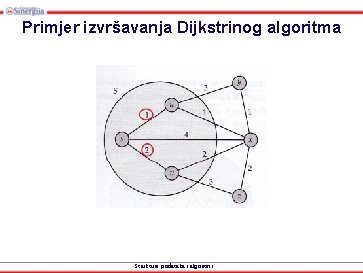
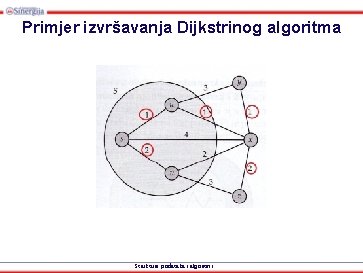
Primjer izvršavanja Dijkstrinog algoritma • Najkraći putevi od čvora s: Strukture podataka i algoritmi

Primjer izvršavanja Dijkstrinog algoritma • Najkraći putevi od čvora s: Strukture podataka i algoritmi

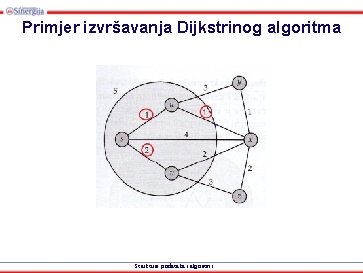
Primjer izvršavanja Dijkstrinog algoritma Strukture podataka i algoritmi

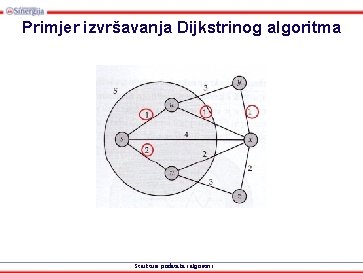
Primjer izvršavanja Dijkstrinog algoritma Strukture podataka i algoritmi

Primjer izvršavanja Dijkstrinog algoritma Strukture podataka i algoritmi

Primjer izvršavanja Dijkstrinog algoritma Strukture podataka i algoritmi

Implementacija Dijkstrinog algoritma • Za težinski graf G sa n čvorova i m grana izvršava se n-1 iteracija dodavanja novog čvora x skupu S. • Da se ne bi nepotrebno u svakoj iteraciji ponovo izračunavale dužine najkraćih specijalnih puteva do čvorova u V-S, one se čuvaju u nizu d dužine n koji je indeksiran čvorovima grafa G. Strukture podataka i algoritmi

Implementacija Dijkstrinog algoritma • Nakon dodavanja izabranog čvora x skupu S mora se uzeti u obzir da je čvor x riješen i da možda postoje kraći specijalni putevi koji vode do njegovih susjeda. • Zbog toga se mora provjeriti vrijednost d(v) za svaki neriješen čvor v koji je susjedan čvoru x. • Ova operacija podešavanja dužine najkraćeg specijalnog puta do neriješenog čvora se naziva popuštanje. Strukture podataka i algoritmi

Popuštanje u Dijkstrinovom algoritmu • • • Za svaki neriješen čvor v koji je susjedan riješenom čvoru x, novi specijalni put do v prati put od s do x u novom S i završava se granom {x, v}. Taj novi specijalni put ima dužinu d(x)+l(x, v). Ako je ta dužina kraća od postojećeg najkraćeg specijalnog puta do v dužine d(v), ta stara vrijednost d(v) se mora ažurirati vrijednošću d(x)+l(x, v). Strukture podataka i algoritmi

Dijkstrin algoritam // Ulaz: težinski graf G, čvor s u G // Izlaz: niz d dužina najkraćih puteva od s do svih čvorova G algorithm dijkstra(G, s) S = {s}; d(s) = 0; for (svaki čvor v različit od s u G) do if ({s, v} grana u G) then d(v) = l(s, v); // dužina grane između s i v else d(v) = ∞; // beskonačna dužina while (S je pravi podskup od V) do Odrediti čvor x u V-S za koji je d[x] najmanje; S = S + x; for (svaki čvor v u V-S koji je spojen granom sa x) do d[v] = min{d[v], d[x] + l(x, v) }; // popuštanje return d; Strukture podataka i algoritmi

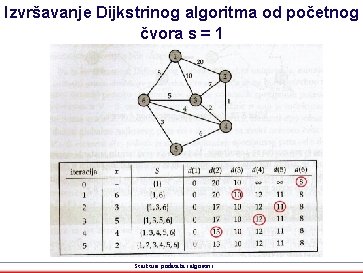
Izvršavanje Dijkstrinog algoritma od početnog čvora s = 1 Strukture podataka i algoritmi

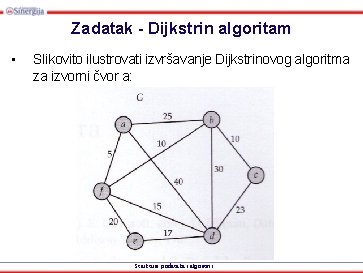
Zadatak - Dijkstrin algoritam • Slikovito ilustrovati izvršavanje Dijkstrinovog algoritma za izvorni čvor a: Strukture podataka i algoritmi

Najkraći putevi između svih čvorova • Problem najkraćih puteva između svih čvorova sastoji se u nalaženju najkraćih puteva između svaka dva čvora u težinskom grafu G. • Jedan način za rješavanje ovog problema jeste višestruko izvršavanje Dijkstrinog algoritma od svakog čvora grafa. • Drugi način je primjenjujući Flojdov algoritam. Strukture podataka i algoritmi

Flojdov algoritam • Neka je G = (V, E) težinski graf i neka su svi čvorovi grafa G proizvoljno numerisani tako da je V = {v 1, v 2, . . . , vn}. • Flojdov algoritam se zasniva na ideji da se nalaženje najkraćeg puta između bilo koja dva čvora vi i vj podijeli na nalaženje dva najkraća puta: - jednog puta od vi do nekog posrednog čvora, - drugog puta od tog posrednog čvora do vj. Strukture podataka i algoritmi

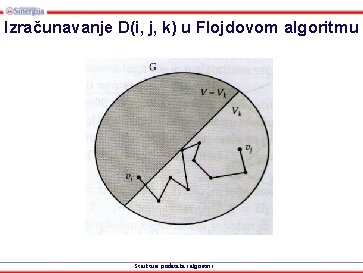
Flojdov algoritam • Najkraći put od vi do vj određuje se koristeći na tom putu samo posredne čvorove iz skupa prvih k čvorova Vk = {v 1, v 2, . . . , vk}. • Taj postupak se ponavlja redom za svako k = 1, 2, . . . , n pri čemu se dužina najkraćeg puta D(i, j, k) izračunava pomoću izraza: D(i, j, k) = min {D(i, j, k-1), D(i, k, k-1) + D(k, j, k-1)} Strukture podataka i algoritmi

Izračunavanje D(i, j, k) u Flojdovom algoritmu Strukture podataka i algoritmi

Flojdov algoritam // Ulaz: težinski graf G predstavljen matricom susjedstva M // Izlaz: matrica D takva da je D(i, j, n) = d(v i, vj) algorithm floyd(G) for i = 1 to n do for j = 1 to n do D[i, j, 0] = M[i, j]; for k = 1 to n do for i = 1 to n do for j = 1 to n do D[i, j, k] = min {D[i, j, k-1], D[i, k, k-1]+D[k, j, k-1]}; return D; Strukture podataka i algoritmi

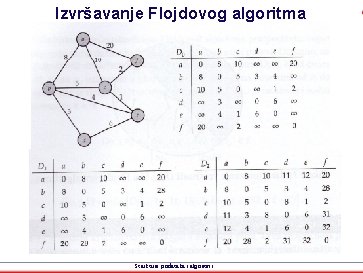
Izvršavanje Flojdovog algoritma Strukture podataka i algoritmi

Izvršavanje Flojdovog algoritma Strukture podataka i algoritmi

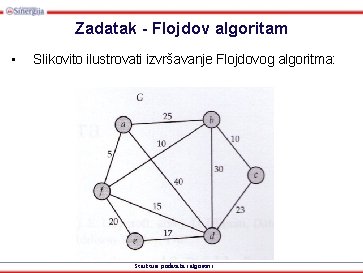
Zadatak - Flojdov algoritam • Slikovito ilustrovati izvršavanje Flojdovog algoritma: Strukture podataka i algoritmi

Zaključak • Težinski grafovi su grafovi čijim granama je dodjeljena neka numerička vrijednost tzv. težina. • Težinski grafovi se predstavljaju pomoću matrice susjedstva i pomoću liste susjedstva. • Minimalno povezujuće stablo T težinskog grafa G = (V, E) je podgraf (V, T) grafa G čiji je zbir težina grana minimalan. Strukture podataka i algoritmi

Zaključak 2 • Algoritmi za određivanje minimalnog povezujućeg stabla: Kruskalov algoritam i Primov algoritam. • Problem najkraćih puteva od jednog čvora sastoji se u tome da se za dati čvor s u težinskom grafu G odrede najkraći putevi od tog čvora s do svih ostalih čvorova u grafu G - Dijkstrin algoritam. • Problem najkraćih puteva između svih čvorova sastoji se u nalaženju najkraćih puteva između svaka dva čvora u težinskom grafu G - Flojdov algoritam. Strukture podataka i algoritmi

Hvala na pažnji! Strukture podataka i algoritmi
 Strukture podataka i algoritmi
Strukture podataka i algoritmi Strukture i vrste podataka u pythonu
Strukture i vrste podataka u pythonu Programski jezici i strukture podataka
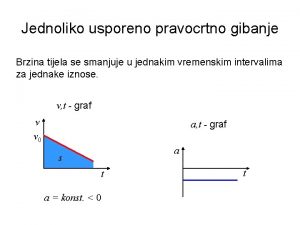
Programski jezici i strukture podataka Jednoliko ubrzano i usporeno gibanje
Jednoliko ubrzano i usporeno gibanje Grafovi matematika
Grafovi matematika Kvadrātfunkcijas grafika konstruēšana ar pārvietojumu
Kvadrātfunkcijas grafika konstruēšana ar pārvietojumu Hamiltonova kontura
Hamiltonova kontura V-t graf jednoliko pravocrtno gibanje
V-t graf jednoliko pravocrtno gibanje Tgx graf
Tgx graf Jednoliko ubrzano gibanje st graf
Jednoliko ubrzano gibanje st graf Sinus graf
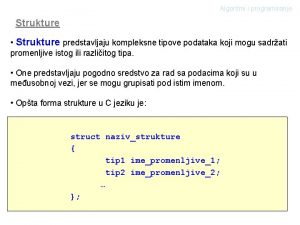
Sinus graf Strukture c++
Strukture c++ матрична структура
матрична структура Konvencionalne radiološke metode
Konvencionalne radiološke metode Funkcionalni model organizacione strukture
Funkcionalni model organizacione strukture Funkcionalna organizaciona struktura
Funkcionalna organizaciona struktura Tipovi organizacione strukture
Tipovi organizacione strukture Induktivni efekat
Induktivni efekat Petlje u programiranju
Petlje u programiranju Ciklicne strukture
Ciklicne strukture Opsti racio likvidnosti
Opsti racio likvidnosti Krovna struktura
Krovna struktura Renaturacija
Renaturacija Bfs algoritmo
Bfs algoritmo Reprezentarea algoritmilor
Reprezentarea algoritmilor Webnstudy
Webnstudy Primjer algoritma iz svakodnevnog života
Primjer algoritma iz svakodnevnog života Algoritmi i programiranje
Algoritmi i programiranje Algoritam matematika
Algoritam matematika Vārdiskais algoritms
Vārdiskais algoritms Znanje org algoritmi
Znanje org algoritmi Algoritmi genetici
Algoritmi genetici Ordonarea cifrelor unui numar c++
Ordonarea cifrelor unui numar c++ Ako poskladat rozlozenu rubikovu kocku
Ako poskladat rozlozenu rubikovu kocku Algoritam informatika
Algoritam informatika Algoritmo dfs
Algoritmo dfs Machine learning algoritmi
Machine learning algoritmi Ordonarea unui vector
Ordonarea unui vector Algoritmi notevoli
Algoritmi notevoli Razgranati algoritmi
Razgranati algoritmi Teoria degli algoritmi
Teoria degli algoritmi Vertex cover esempio
Vertex cover esempio Primeri algoritama iz svakodnevnog zivota
Primeri algoritama iz svakodnevnog zivota Ciklicni algoritmi zadaci i resenja
Ciklicni algoritmi zadaci i resenja Algoritmo finito
Algoritmo finito Linijska struktura zadaci
Linijska struktura zadaci Machine learning algoritmi
Machine learning algoritmi Algoritmi elementari
Algoritmi elementari Camil demetrescu
Camil demetrescu Introduzione agli algoritmi e strutture dati
Introduzione agli algoritmi e strutture dati Ricerca binaria c++
Ricerca binaria c++