Algoritmi i strukture podataka 211 Literatura 1 Dovedan

Algoritmi i strukture podataka (2+1+1) Literatura: 1. Dovedan: Pascal i programiranje, ZOTK, Ljubljana, 1989. 2. Budin: Informatika 2, Element, Zagreb, 1998. 3. Lipschutz: Theory and Problems of Data Structures, Mc Graw Hill, 1986. 4. Knuth: The Art of Computer Programming, Vol. 1. Fundamental Algorithms, Vol. 2. Seminumerical Algorithms, Addison Wesley, 1997. 5. Lipschutz, Lipson: Discrete Mathematics, Mc Graw Hill, New York 1997.

Sadržaj predmeta: 1. Osnovni pojmovi 2. Elementarni podaci 3. Slučajni brojevi 4. Linearne strukture a) Vektori i matrice b) Stogovi c) Redovi 5. Nelinearne strukture a) Stabla b) Grafovi 6. Rekurzije

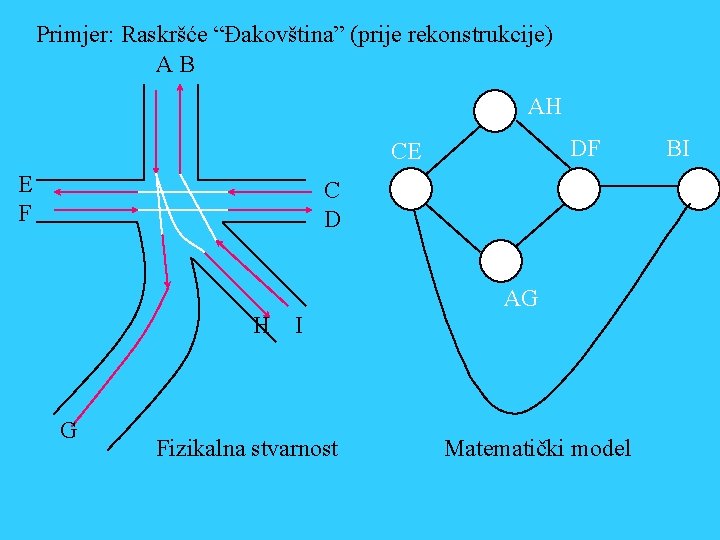
1. Osnovni pojmovi: Algoritam (po Muhammad ibn Musa al-Kwarizm): opis postupka koji nakon konačnog broja radnji daje suvisli rezultat. Alogoritam je i dio posla u procesu koji od uočenog problema dovodi do rezultata (najčešće pomoću računalnog programa). Slijed poslova: do{ S/= V[i++]; Ponavljati. . . . Sve dok. . Fizikalna stvarnost Matematički model ALGORITAM }while Struktura podataka . . . Računalni program

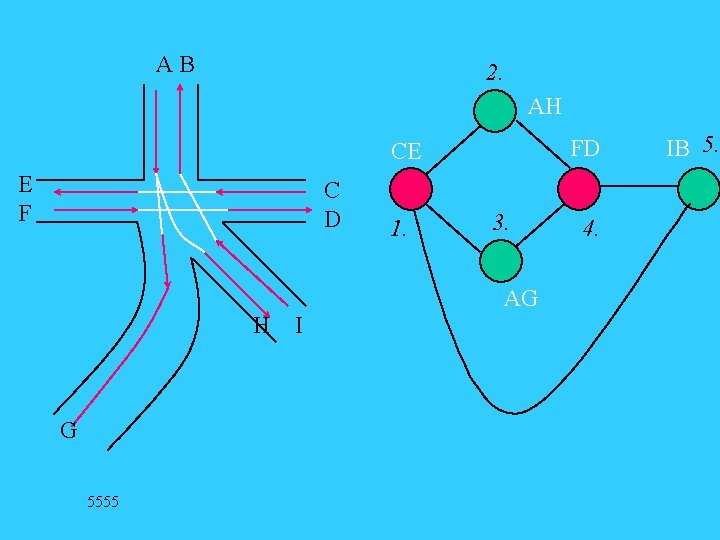
Primjer: Raskršće “Đakovština” (prije rekonstrukcije) AB AH DF CE E F C D AG H G I Fizikalna stvarnost Matematički model BI

AB 2. AH FD CE E F C D 1. 3. AG H G 5555 I 4. IB 5.

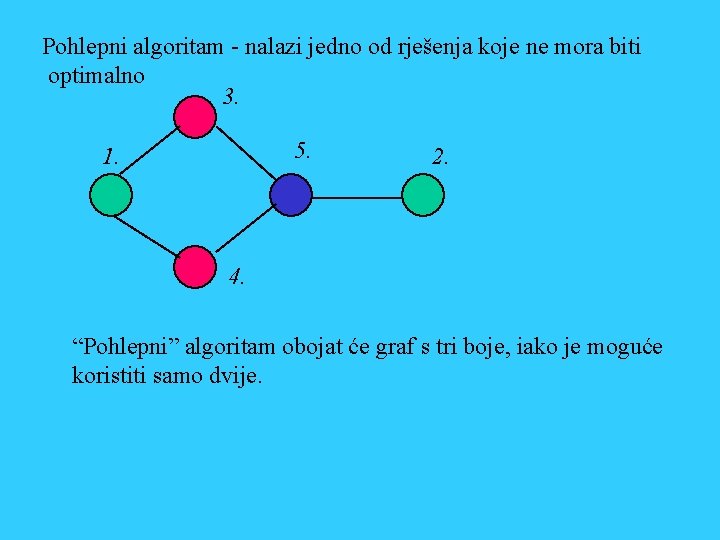
Pohlepni algoritam - nalazi jedno od rješenja koje ne mora biti optimalno 3. 5. 1. 2. 4. “Pohlepni” algoritam obojat će graf s tri boje, iako je moguće koristiti samo dvije.

Algoritam bojanja grafa: Boja=1 Sve dok graf nije obojan Obavljaj bojanje(Boja) Povećaj Boja za 1 Kraj sve dok Algoritam procedure bojanje (Boja) /*Neobojane čvorove čiji susjedi nisu obojani bojom Boja obojaj bojom Boja*/ Stavi 0 u sve elemente vektora Obojani[] Nađi neobojani čvor i Postavi Obojani[1]=i Postavi nb=1 Naznači da je i-ti čvor obojan bojom Boja Za svaki čvor j grafa činiti Ako je čvor j neobojan i njegovi susjedi nisu u vektoru Obojani[] postavi boju čvora j na Boja

2. Elementarni podaci a) Znakovi 8 bitni ASCII kod definira 256 znaka (kontrolni i grafički - vidljivi) Dec Hex Char 0 00 Nul 1 01 SOH. . . 32 20 (blank). . . . 65 41 A. . . . 97 61 a. . . . 159 9 F č Problem specijalnih “nacionalnih” znakova (u hrvatskom ČĆĐŠŽ). Rješenje: Kodna stranica (Code Page - CP) Npr. CP 852 Č 172 č 159 Ć 143 ć 134 Đ 209 đ 208 Š 230 š 231 Ž 166 ž 167

b) Brojevi A) Cijeli brojevi Pozicioni brojni sustav Definirano: Baza B i znamenke di s vrijednostima [0, B-1] Broj N napisan nizom od n znamenaka dn-1, dn-2, . . . , d 2, d 1, d 0 ima vrijednost N= Kod za cijele brojeve definira pomoću bitova (znamenaka 0 i 1) pozitivne i negativne brojeve. Negativni brojevi definirani su preko dualnog komplementa

Komplement broja u pozicionom sustavu s bazom B definiran je kao: n n komp(N)=B -N | B > N Komplementiranje binarnog broja (B=2) zove se dualno komplementiranje. Obavlja se u dva koraka: 1. Unarno kompementirati broj (0 ->1 i 1 ->0) 2. Aritmetički dodati 1 n n DOKAZ: komp(N)= 2 n n = 2+ n =2 + =2 =2 + n -2 +1= = +1 =

Algoritam binarnog komplementiranja (broj je u vetoru V[] od 16 bitova) Za svaki i=0 do 15 činiti Ako je V[i]=1 postaviti V[i]=0 U suprotnom postaviti V[i] = 1 Kraj za svaki i Postaviti i=0 Ponavljati Ako je V[i]=1 postaviti V[i]=0 U suprotnom postaviti V[i] = 1 Povećati i za 1 Sve dok je V[i-1]=0

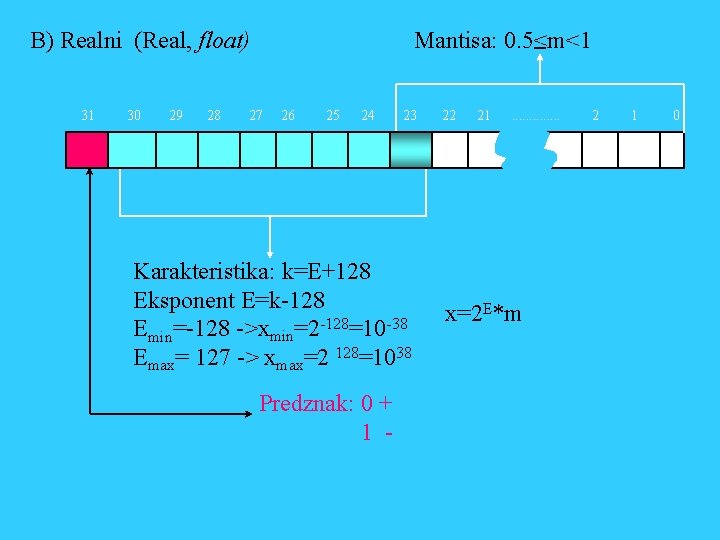
B) Realni (Real, float) 31 30 29 28 Mantisa: 0. 5<m<1 27 26 25 24 23 Karakteristika: k=E+128 Eksponent E=k-128 Emin=-128 ->xmin=2 -128=10 -38 Emax= 127 -> xmax=2 128=1038 Predznak: 0 + 1 - 22 21 . . . x=2 E*m 2 1 0

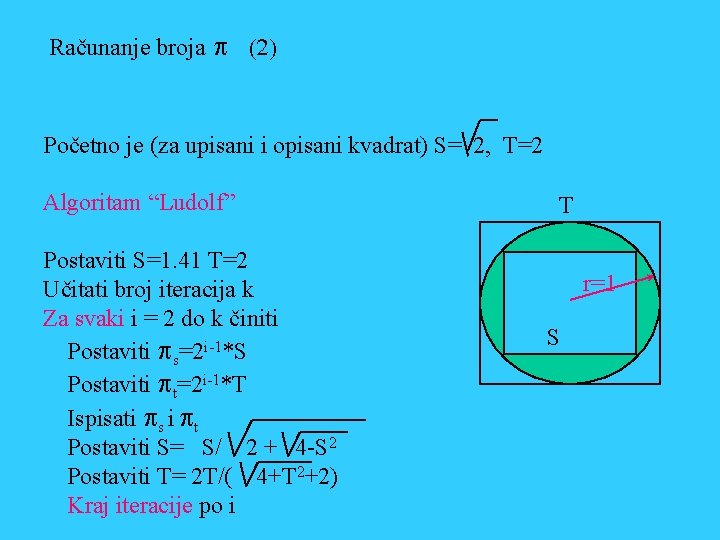
Pogreške u aritmetici kliznog zareza Najčešće uslijed konačnog broja binarnih (dekaskih) znamenaka u mantisi (24 binarne znamenke daju 7 točnih dekadskih znameki: Primjer : Računanje broja p Ludolfovom metodom: Sn Sn+1 ln 2 = S 2 n+1 -(Sn/2)2 (1 -ln)2 = 1 -(sn/2)2 ln Sn+1 = 2 - 4 -(Sn/2)2 Prilagođeno za Sn+1 numerički račun: = Sn/ 2 + 4 -Sn 2 Za opisane mnogokutnike: Tn+1=2 Tn/( 4+Tn 2 +2) Za i-tu iteraciju je p=2 i-1 Si

Računanje broja p (2) Početno je (za upisani i opisani kvadrat) S= 2, T=2 Algoritam “Ludolf” Postaviti S=1. 41 T=2 Učitati broj iteracija k Za svaki i = 2 do k činiti Postaviti ps=2 i-1*S Postaviti pt=2 i-1*T Ispisati ps i pt Postaviti S= S/ 2 + 4 -S 2 Postaviti T= 2 T/( 4+T 2+2) Kraj iteracije po i T r=1 S

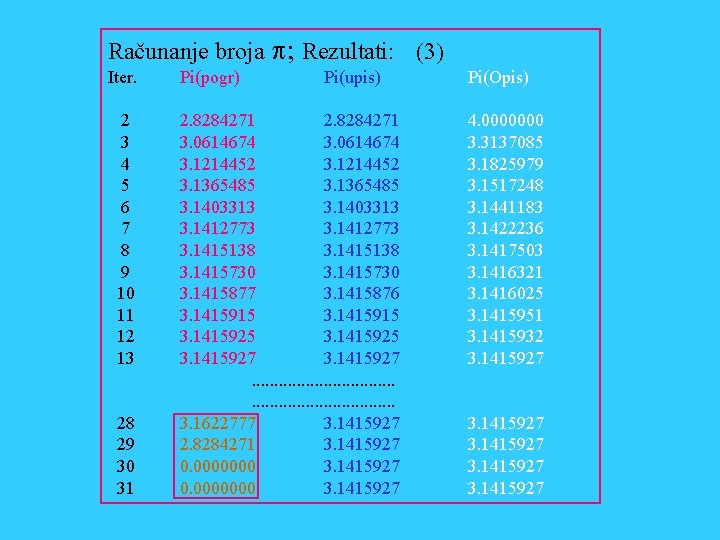
Računanje broja p; Rezultati: (3) Iter. 2 3 4 5 6 7 8 9 10 11 12 13 28 29 30 31 Pi(pogr) Pi(upis) 2. 8284271 3. 0614674 3. 1214452 3. 1365485 3. 1403313 3. 1412773 3. 1415138 3. 1415730 3. 1415877 3. 1415876 3. 1415915 3. 1415925 3. 1415927. . . . 3. 1622777 3. 1415927 2. 8284271 3. 1415927 0. 0000000 3. 1415927 Pi(Opis) 4. 0000000 3. 3137085 3. 1825979 3. 1517248 3. 1441183 3. 1422236 3. 1417503 3. 1416321 3. 1416025 3. 1415951 3. 1415932 3. 1415927

3. Slučajni brojevi Niz brojeva u kojem je svaki član nezavisan od prethodnih je niz slučajnih brojeva (engl. Random Numbers). Programski jezici obično sadrže funkciju koja generira jednoliko raspodjeljene (npr. RND, random). Brojevi su jednoliko raspoređeni (distribuirani) u definiranom intervalu, ako su vjerojatnosti pojavljivanja, u bilo kojem podintervalu iste širine Dx, međusobno jednake.

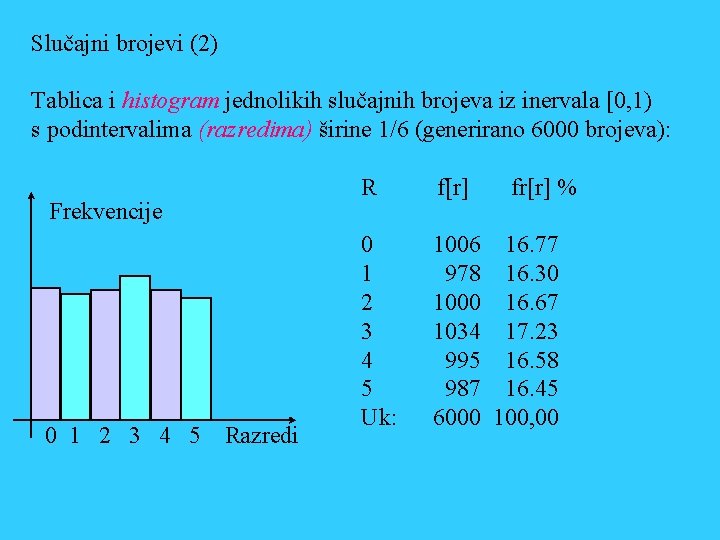
Slučajni brojevi (2) Tablica i histogram jednolikih slučajnih brojeva iz inervala [0, 1) s podintervalima (razredima) širine 1/6 (generirano 6000 brojeva): Frekvencije 0 1 2 3 4 5 Razredi R f[r] fr[r] % 0 1 2 3 4 5 Uk: 1006 16. 77 978 16. 30 1000 16. 67 1034 17. 23 995 16. 58 987 16. 45 6000 100, 00

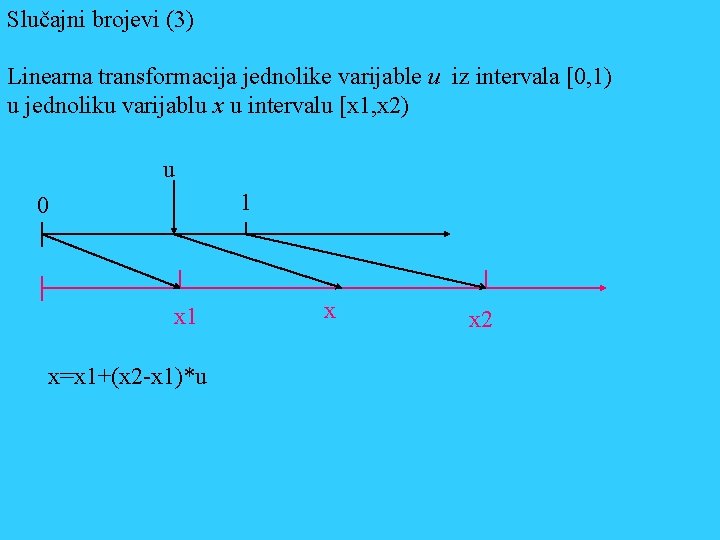
Slučajni brojevi (3) Linearna transformacija jednolike varijable u iz intervala [0, 1) u jednoliku varijablu x u intervalu [x 1, x 2) u 1 0 x 1 x=x 1+(x 2 -x 1)*u x x 2

Slučajni brojevi (4) Algoritam “Histogram”: Generirati m jednoliko raspodijeljenih slučajnih brojeva u intervalu [x 1, x 2) i razvrstati ih u histogram s n razreda jednake širine sr. Učitati m, n, x 1 i x 2 Za svaki i=0 do n-1 postaviti Hist[i]=0 Postaviti sr=(x 2 -x 1)/n Za svaki i=1 do m činiti Generirati x=x 1+(x 2 -x 1)*u Postaviti k=(x-x 1)/sr Povećati Hist[k] za 1 Kraj iteracije Za svaki i=0 do n ispisati Hist[i]

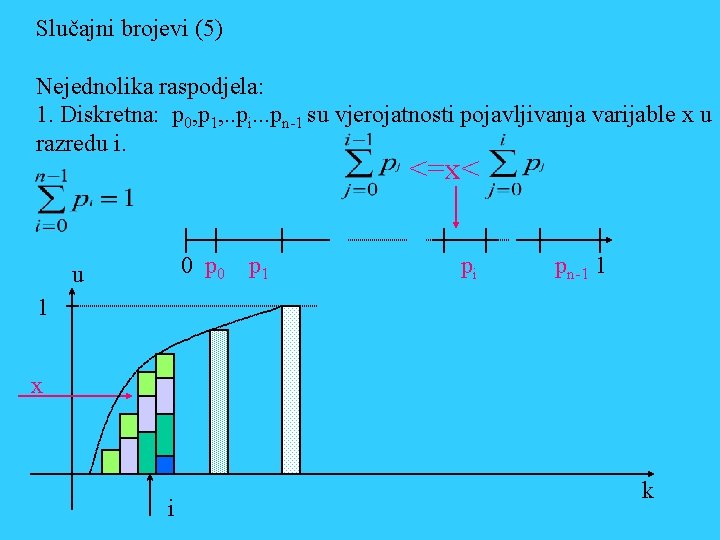
Slučajni brojevi (5) Nejednolika raspodjela: 1. Diskretna: p 0, p 1, . . pi. . . pn-1 su vjerojatnosti pojavljivanja varijable x u razredu i. <=x< 0 p 1 u pi pn-1 1 1 x i k

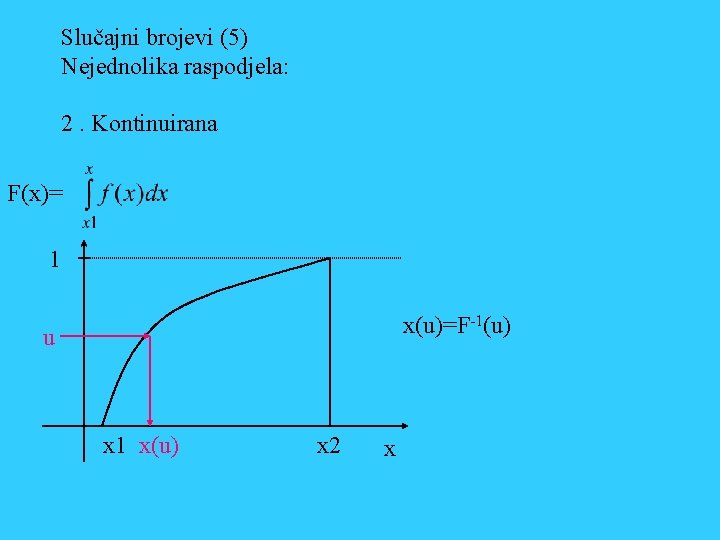
Slučajni brojevi (5) Nejednolika raspodjela: 2. Kontinuirana F(x)= 1 x(u)=F-1(u) u x 1 x(u) x 2 x

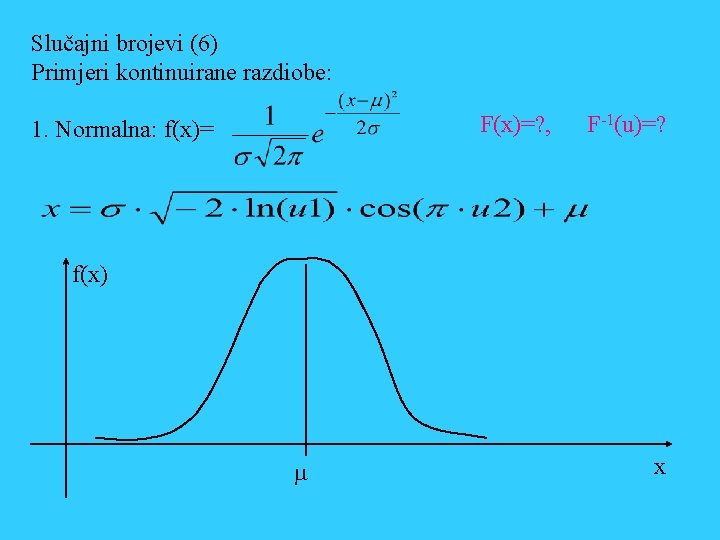
Slučajni brojevi (6) Primjeri kontinuirane razdiobe: F(x)=? , 1. Normalna: f(x)= F-1(u)=? f(x) m x

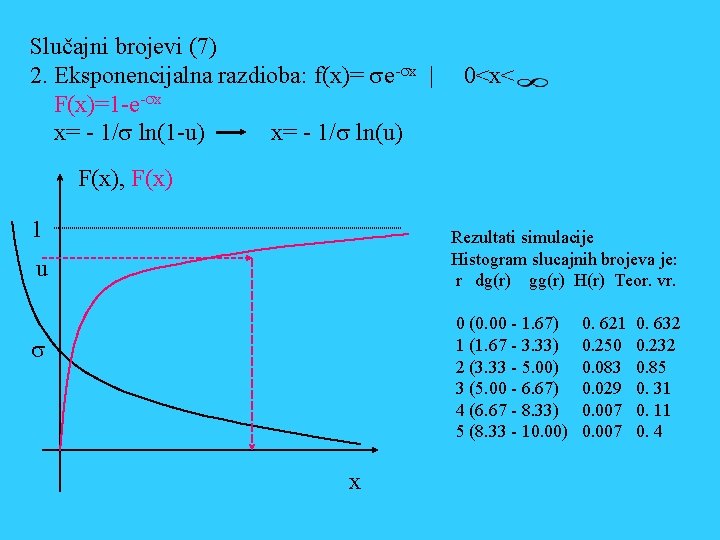
Slučajni brojevi (7) 2. Eksponencijalna razdioba: f(x)= se-sx | F(x)=1 -e-sx x= - 1/s ln(1 -u) x= - 1/s ln(u) 0<x< F(x), F(x) 1 Rezultati simulacije Histogram slucajnih brojeva je: r dg(r) gg(r) H(r) Teor. vr. u 0 (0. 00 - 1. 67) 1 (1. 67 - 3. 33) 2 (3. 33 - 5. 00) 3 (5. 00 - 6. 67) 4 (6. 67 - 8. 33) 5 (8. 33 - 10. 00) s x 0. 621 0. 250 0. 083 0. 029 0. 007 0. 632 0. 232 0. 85 0. 31 0. 11 0. 4

4. Linearne strukture 4. 1 Vektori i matrice: 4. 1. 1 Vektori: “jednodimenzionalna” linearna struktura podataka. Svi članovi su istog tipa. V[] V[0] V[1] Algoritmi s vektorima: a) Pretraživanja: Za zadani podatak X naći da li se on nalazi u skupu V[] i na kojem mjestu. V[i] a. 1) Sekvencijelno pretraživanje. Postaviti i=0 Sve dok je V[i]!=X i i<n-1 povećati i za 1. Ako je i<n naznačiti da je X na i-tom mjestu. U suprotnom naznačiti da i nije u skupu V. V[n-1]

a 2) Binarno pretraživanje: Skup je uređen (V[i]<=V[i+1] za i=(0, n-2) ) dg=0 s=(dg+gg)/2 gg=n-1 Postaviti dg=0, Postaviti gg=n-1 Ponavljati Postaviti s=(dg+gg)/2 Ako je X>V[s] postaviti dg=s+1; Ako je X<V[s] postaviti gg=s-1; Do uvjeta V[s]=X ili gg=dg Ako je V[s]=X naznačitida je X na s-tom mjestu u skupu. U suprotnom naznačiti da X nije u skupu

Algoritam “Iduća permutacija” Zadan je vektor V od n elemenata u kojem je početno V[i]=i. To je prva permutacija podataka u V. Zadnja permutacija od (ukupno n!) je takva da je V[i]=n-1 -i. Ako je zadana neka m-ta permutacija, naći m+1. permurtaciju. Primjer: P 0 = 0 1 2 3 4 5 Pm = 0 1 2 5 4 3 Naći Pm+1 (Pm+1 = 0 1 3 2 4 5 ) Rješenje: Naći najveći i za koji vrijedi V[i]<V[i+1] (Procedura Nadji_i) Naći i < j < n tako da je V[j] najmanja vrijednost uz uvjet V[j]>V[i] (Procedura Nadji_j) Zamijeniti V[j] s V[i] Poredati elemente V[k] , k>i u rastućem redoslijedu

Algoritam procedure “Nadji_i” Postaviti i=n-1 Sve dok je V[i-1]<V[i] smanjiti i za 1 Smanjiti i za 1 Algoritam procedure “Nadji_j” Postaviti j=i+1 Za svaki k=i+1 do n-1 činiti Ako je V[k]>V[i] i V[k]<V[j] postaviti j=k

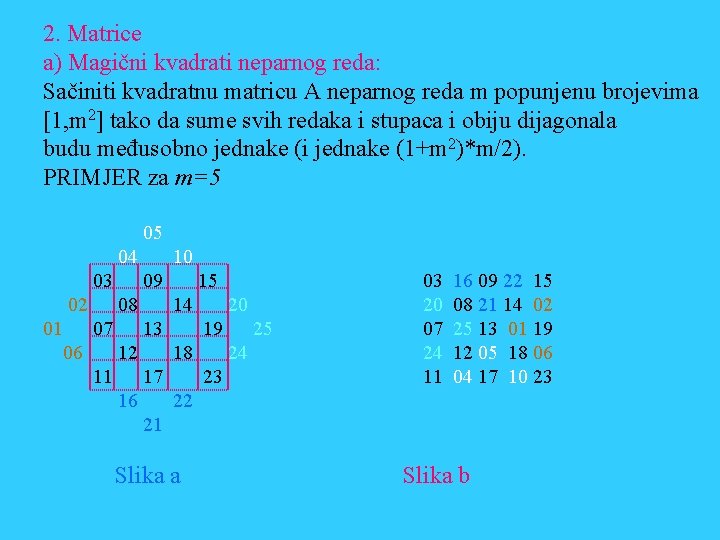
2. Matrice a) Magični kvadrati neparnog reda: Sačiniti kvadratnu matricu A neparnog reda m popunjenu brojevima [1, m 2] tako da sume svih redaka i stupaca i obiju dijagonala budu međusobno jednake (i jednake (1+m 2)*m/2). PRIMJER za m=5 05 04 03 02 01 10 09 08 07 06 15 14 13 12 11 20 19 18 17 16 25 24 23 03 20 07 24 11 16 09 22 15 08 21 14 02 25 13 01 19 12 05 18 06 04 17 10 23 22 21 Slika a Slika b

Algoritam “Magični kvadrat” Učitati m /* m mora biti neparan*/ /* Popuniti matricu prema slici a procedurom Popuni */ Pozvati proceduru Popuni(A[][], m) /* Obaviti prebacivanja u matrici da bi se dobila slika b Pozvati proceduru Prebaci(A[][], m, ”lijevo”) Pozvati proceduru Prebaci(A[][], m, ”desno”) Pozvati proceduru Prebaci(A[][], m, ”gore”) Pozvati proceduru Prebaci(A[][], m, ”dolje”) */ /*Ispisati matricu A od m/2 do m/2+m-1 procedurom Ispis*/ Pozvati proceduru Ispis(A[][], m)

Algoritam procedure “Popuni” Za svaki i=0 do 2*m-2 činiti Za svaki j=0 do 2*m-2 postaviti A[i][j]=0 Postaviti i=m-1 /*Počni od srednjeg reda */ Postaviti j=0 /* Počni od lijevog stupca */ Postaviti n=1 Sve dok je n<=m*m činiti Postaviti A[i][j]=n Smanjiti i za 1 /* Kreni red gore */ Povećati j za 1 /* Kreni stupac u desno */ Povećati n za 1 /* Idući broj u matrici */ Ako je n-1 djeljivo s m činiti Povećati i za m+1 /* Ponovo počni red niže. . . */ Smanjiti j za m-1 /*. . i stupac dalje */ Kraj ako je Kraj sve dok

Algoritam procedure “Prebaci(A[][], m, ”desno”)” Za svaki j=0 do m/2 -1 činiti Za svaki i=0 do 2*m-2 činiti Ako je A[i][j]!=0 postaviti A[i+m][j]=A[i][j] Procedure prebacivanja u ostalim smjerovima su analogne ovoj

b) Inveriranje matrice Gaussovom metodom: A*A-1= I X 1*A*A-1= X 1*I X 2*X 1*A*A-1= X 2*X 1*I X 3*X 2*X 1*A*A-1= X 3*X 2*X 1*I Xn*. . X 3*X 2*X 1*A*A-1= Xn*. . X 3*X 2*X 1*I Ako Xn*. . X 3*X 2*X 1*A postane I onda lijeva je strana jednaka I*A-1 tj. A-1, pa je tome jednaka i desna strana: Ako se nizom transformacija (što odgovara množenju s Xi) početna matrica pretvori u jediničnu, tim istim transformacijama se jedinična pretvori u inverznu! Xn*. . X 3*X 2*X 1*A*A-1= Xn*. . X 3*X 2*X 1*I

Algoritam “INVMAT” Učitati matricu A[m][m] Formirati jediničnu matricu I u stupcima m do 2*m-1 matrice A (A postaje tkzv. blok matrica) Postaviti d=1 Postaviti i=0 Sve dok je i<m-1 i d!=0 činiti Ako je A[i][i]=0 pozvati proceduru Zamjena(i, d) Ako je d!=0 pozvati proceduru Redukcija(i, d) Kraj sve dok Pozvati proceduru Ispis(d)

Algoritam procedure “Zamjena(i, d)” Za svaki k=i+1 do m-1 činiti Ako je A[k][i]!=0 onda činiti Za svaki j=i do 2*m-1 činiti Postaviti t=A[k][j] Postaviti A[k][j]=A[k][i] Postaviti A[k][i]=t Kraj za svaki j Postaviti d = - d Vratiti se u pozivajuću proceduru Kraj ako je Kraj za svaki k Postaviti d = 0 (Napomena: Zamjena sadržaja dviju numeričkih varijabli x i y može se obaviti i ovako: x=y-x; y=y-x; x=x+y; )

Algoritam procedure “Redukcija(i, d)” Pomnožiti d s A[i][i] Za svaki j=2*m-1 do i s korakom -1 podijeliti A[i][j] s A[i][i] Za svaki k=0 do m-1 i k!=i Za svaki j=2*m-1 do i s korakom -1 smanjiti A[k][j] za A[i][j]*A[k][i]

4. 2 Stogovi Stog se sastoji od vektora V[]od n elemenata i pokazivača stoga Sp. Pokazivač stoga ima vrijednost indeksa zadnjeg popunjenog elementa u vektoru V. 5 4 3 2 1 0 Prazni dio stoga Pokazivač stoga Popunjeni Sp=3 dio stoga Stog je prazan ako je Sp = -1 Stog je pun ako je Sp=n-1 Stog se “puni” i “prazni” na “vrhu”. Podatak koji je zadnji stavljen na stog, bit će prvi skinut sa stoga (LIFO - Last In - First out) Stavljenje na stog obavlja procedure Push Skidanje sa stoga obavlja procedura Pop

Funkcija “Prazan_stog” Ako je Sp= - 1 vratiti 1 (True) U suprotnom vratiti 0 (False) Funkcija “Pun_stog” Ako je Sp=n-1 vratiti 1 (True) U suprotnom vratiti 0 (False) Procedura Push /* Stavi x na stog */ Ako je Pun_stog javiti pogrešku U suprotnom Povećati Sp za 1 Postaviti V[Sp]=x Kraj u suprotnom Procedura Pop /* Skini podatak sa stoga i stavi ga u x */ Ako je Prazan_stog javiti pogrešku U suprotnom Postaviti x=V[Sp] Smanjiti Sp za 1 Kraj u suprotnom Procedura Očisti_stog Postaviti Sp= - 1

Algoritam “Putna torba” Zadan je skup od n prirodnih brojeva Tezine i prirodni broj T. Naći bilo koji podskup Torba skupa Tezine tako da zbroj elemenata u Torba bude jednak T. Ako takvog podskupa nema, ispisati odgovarajuću poruku. Procedura Torba Očisti_stog Ponavljati Ako je uk_tez=T postaviti rjes=1 U suprotnom Ako je uk_tez<T i pred <n onda pozvati proceduru u_torbu U suprotnom Pozvati proceduru iz_torbe Ako je pred<n pozvati proceduru u_torbu Kraj u suprotnom sve dok nije rjes i nije prazan_stog

Procedura u_torbu Povećati pred za 1 Povećati uk_tez za Tezine[pred] Pozvati proceduru push(pred) Procedura iz_torbe Pozvati proceduru pop(pred) Smanjiti uk_tez za Tezine[pred] Glavni program Putna_torba Postaviti rjes=0, uk_tez=0 i pred=0 Učitati T i n Za svaki i=1 do n učitati Tezine[i] Pozvati proceduru Torba Ako je rješenje nadjeno Za svaki i=0 do pred-1 ispisati Tezine[predmeti[i]] U suprotnom ispisati poruku da nema rješenja

Algoritam “Povrh” Isprazniti stogove s 1 i s 2 Staviti n na stog s 1 Staviti m na stog s 2 Postaviti Povrh=0 Ponavljati Skinuti n sa stoga s 1 Skinuti m sa stoga s 2 Ako je m=n ili n=1 ili m=0 povećati Povrh za 1 U suprotnom Staviti n-1 na stog s 1 Staviti m-1 na stog s 2 Staviti n-1 na stog s 1 Staviti m na stog s 2 do praznog stoga s 1 Ispisati Povrh

Algoritam “Quick sort” Zadani skup brojeva u vektoru A[ ] poredati po rastućem redoslijedu. Postupak: 1. Naći konačno mjesto m prvog člana skupa (tako da su lijevo od njega svi manji a desno svi veći članovi) 2. Ponavljati taj postupak s podskupovima lijevo i desno od m. Granice podskupova stavljati na stog. 1. Algoritam Nadji_m (dg, gg) /*dg je donja a gg gornja granica u A[] unutar kojih se traži m*/ 12 9 15 7 31 25 19 A[m]>A[g] 7 9 15 12 31 25 19 A[d]>A[m] 7 9 12 15 31 25 19

Ponavljati Postaviti m=dg Sve dok je A[gg]>A[m] i gg<>m smanjiti gg za 1 Ako je gg=m vratiti m Zamijeniti A[m] i A[gg] Postaviti m=gg Sve dok je A[dg]<A[m] i dg<>m povećati dg za 1 Ako je dg=m vratiti m Zamijeniti A[m] i A[dg] Do beskonačnosti

Algoritam Quick Učitati broj podataka n i n podataka u vektor A[] Staviti 0 na stog Staviti n-1 na stog Ponavljati Skinuti g sa stoga Skinuti d sa stoga Postaviti m=Nadji_m(d, g) Ako je d<m-1 onda Staviti d na stog Staviti m-1 na stog Kraj ako je Ako je g>m+1 onda Staviti m+1 na stog Staviti g na stog Kraj ako je Do praznog stoga

4. 3 Redovi (engl. Queue) Red se sastoji od vektora V[]od n elemenata, pokazivača na početak (izlaz) reda iz te pokazivača na kraj (ulaz) reda ul. Pokazivač iz pokazuje na prvi element koji treba izaći iz reda (ako takvog ima tj. ako red nije prazan). Pokazivač ul pokazuje na prvo slobodno mjesto u redu (ako takvog ima tj. ako red nije pun). Podatak koji je prvi ušao u red prvi će i izaći iz reda (FIFO -First in, first out načelo). Postoje konačni i ciklički redovi. 4. 3. 1 Konačni red V 0 iz n-1 ul Funkcija “Prazan_red” Ako je ul= iz-1 vratiti 1 (True) U suprotnom vratiti 0 (False) Funkcija “Pun_red” Ako je ul=n-1 vratiti 1 (True) U suprotnom vratiti 0 (False)

Procedura U_red /* Stavi x u red (Enqueue) */ Ako je Pun_red javiti pogrešku U suprotnom Povećati ul za 1 Postaviti V[ul]=x Kraj u suprotnom Procedura Očisti_red Postaviti ul=0 Postaviti iz=0 Procedura Iz_reda /* Skini podatak iz reda i stavi ga u x (Dequeue) */ Ako je Prazan_red javiti pogrešku U suprotnom Postaviti x=V[iz] Povećati iz za 1 Kraj u suprotnom

4. 3. 2 Ciklički red U cikličkom redu se nakon što se popuni n-1. podatak red i dalje puni od početka tj. od nultog mjesta. n-1 0 1 2 3 U cikličkom redu se ulazni pokazivac povećava izrazom ul=mod(ul+1, n). Isto vrijedi i za izlazni pokazivac. Ciklički red je prazan ako je ul=iz i zadnja promjena bio je izlaz Ciklički red je pun mod(ul+1)=iz i zadnja promjena bio je ulaz

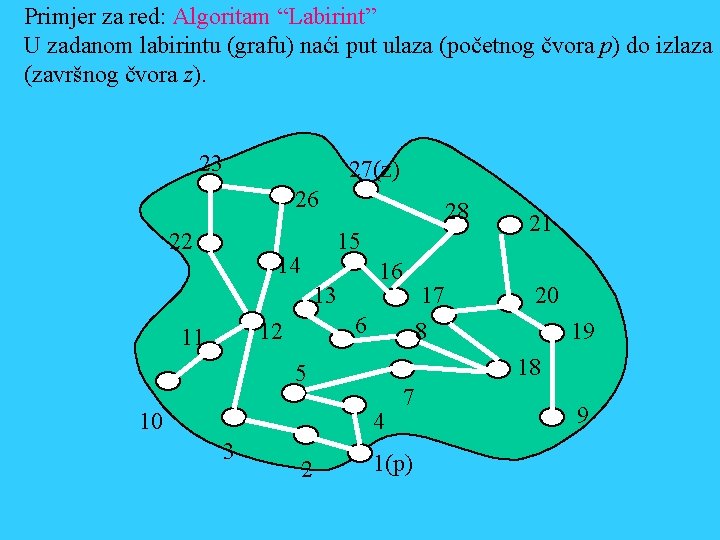
Primjer za red: Algoritam “Labirint” U zadanom labirintu (grafu) naći put ulaza (početnog čvora p) do izlaza (završnog čvora z). 23 27(z) 26 22 28 15 14 16 13 6 12 11 10 4 2 20 19 18 5 3 17 8 21 7 1(p) 9

Algoritam procedure Labirint Za svaki čvor i postaviti Status[i]=0 Postaviti cvor=p Postaviti s=1 Staviti cvor u Red Postaviti Status[cvor]=s Povećati s za 1 Sve dok je cvor!=z i Red nije prazan činiti Izvaditi cvor iz reda Za svaki susjed Su sa Status[Su]=0 činiti Staviti Su u Red Postaviti Status[Su]=s Kraj za svaki susjed Povećati s za 1 Kraj sve dok je Ako je cvor!=z ispisati poruku da puta nema U suprotnom aktivirati proceduru Nadji_put

Algoritam procedure Nadji_put Postaviti Nc=1 Postaviti cvor =z Postaviti Put[0]=z Sve dok je cvor!=p činiti Naći susjed Su čvoru tako da je Status[cvor]>Status[Su] Postaviti Put[Nc]=Su Postaviti cvor=Su Povećati Nc za 1 Kraj sve dok Za svaki i=Nc-1 do 0 ispisati Put[i]

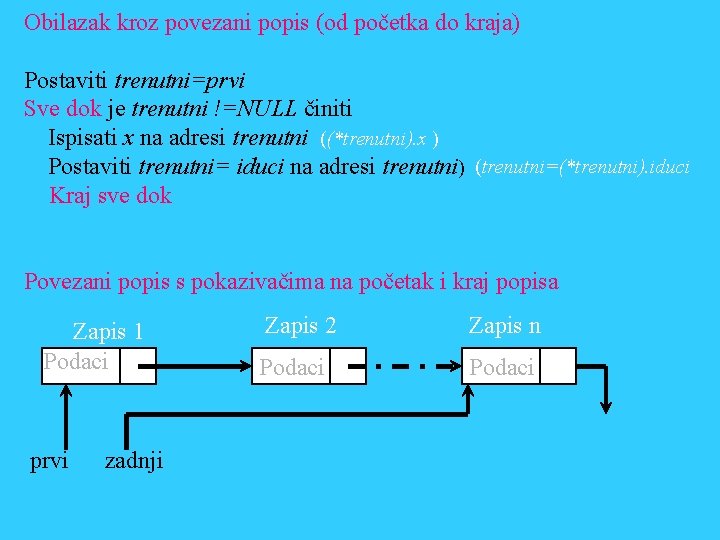
4. 4 Povezani popis (engl. Linked List) je dinamička struktura. Elementi popisa (zapisi) se stavljaju u slobodni dio memorije, a kada pojedini zapis ili cijeli popis više nije potreban, zauzeti dio memorije se oslobađa. Elementi su međusobno povezani adresnim podacima pokazivačima (engl. Pointer). Redoslijed po kojemu se sekvencijelno prolazi kroz popis može se mijenjati mijenjajući samo vrijednosti pokazivača. Zapis 1 Podaci Prvi Zapis 2 Zapis 3 Podaci Pokazivači na idući zapis

Stvaranje povezanog popisa: Postaviti prvi=NULL Učitati podatak y Sve dok nije kraj podataka činiti Ako je prvi=NULL činiti Postaviti trenutni=nova adresa u dinamičkoj memoriji (procedurom malloc u C-u ili New u Pascalu) Postaviti prvi=trenutni U suprotnom činiti Postaviti prethodni=trenutni Postaviti trenutni=nova adresa u dinamičkoj memoriji Postaviti iduci na adresi prethodni = trenutni Kraj ako je Postaviti x na adresi trenutni = y ( (*trenutni. x)=y ) Učitati podatak y Kraj sve dok Postaviti iduci na adresi trenutni = NULL ( (*trenutni). iduci=NULL )

Obilazak kroz povezani popis (od početka do kraja) Postaviti trenutni=prvi Sve dok je trenutni !=NULL činiti Ispisati x na adresi trenutni ((*trenutni). x ) Postaviti trenutni= iduci na adresi trenutni) (trenutni=(*trenutni). iduci Kraj sve dok Povezani popis s pokazivačima na početak i kraj popisa Zapis 1 Podaci prvi zadnji Zapis 2 Zapis n Podaci

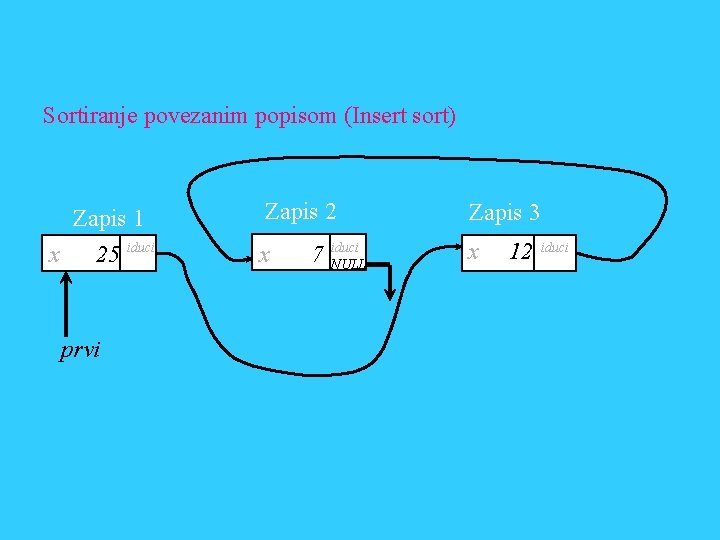
Sortiranje povezanim popisom (Insert sort) Zapis 1 x 25 prvi iduci Zapis 2 x 7 iduci NULL Zapis 3 x 12 iduci

Algoritam “Insert sort” (padajući redoslijed) Postaviti pokazivač prvi=NULL Učitati podatak y Sve dok nije kraj podatak y činiti Pozvati proceduru Insert_sort(y) Učitati podatak y Kraj sve dok Procedura Insert_sort(y) Naći slijedeću slobodnu adresu adr Staviti y u podatak x na adresi adr Ako je prvi=NULL činiti Postaviti iduci na adresi adr na NULL Postaviti prvi=adr U suprotnom činiti Postaviti prethodni=NULL Postaviti trenutni=prvi /* (*adr). x=y */ /* Prvi podatak */ /* (*adr). iduci=NULL */ /* Svi ostali osim prvog*/

Sve dok je x na adresi trenutni veći od y i nije kraj popisa činiti Ako je došao najveći činiti /* Najveći podatak */ Postaviti prvi=adr Postaviti iduci na adresi prvi = trenutni U suprotnom /* Opći slučaj */ Postaviti iduci na adresi adr=iduci na adresi prethodni Postaviti iduci na adresi prethodni = adr Kraj ako je U suprotnom /* Najmanji podatak */ Postaviti iduci na adresi trenutni = adr Postaviti iduci na adresi adr=NULL Kraj ako je Kraj sve dok Kraj ako je

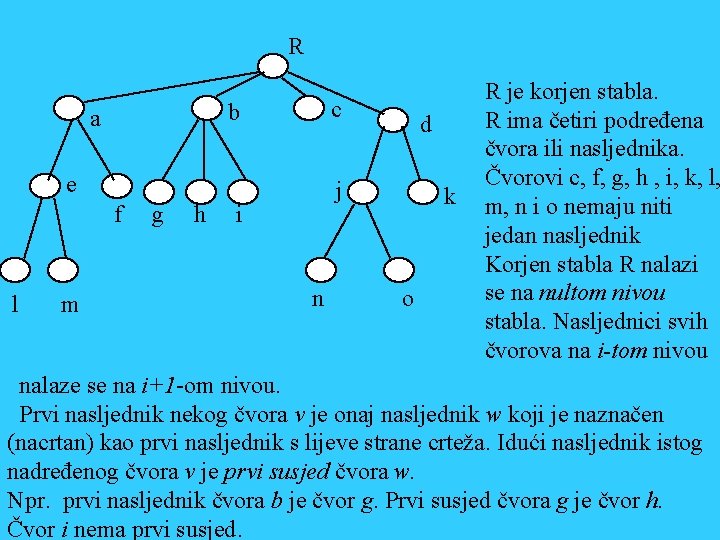
5. Nelinearne strukture 5. 1. Stabla Stablo je hijerarhijska struktura koja se sastoji od čvorova i grana. Čvorovi su “točke” (ili kružići u grafičkom prikazu), koji su spojeni dužinama koje se nazivaju granama. Hijerarhijska struktura stabla uočava se iz činjenice, da čvorovi mogu imati podređene čvorove (povezane granama “prema dolje”) i najviše jedan nadređeni čvor (povezan granom “prema gore”). Svi čvorovi osim jednog, koji se zove korjen imaju jedan nadređeni čvor. Korjen nema nadređeni čvor. Stablo na slici naziva se općim stablom jer broj podređenih čvorova može biti proizvoljan.

R c b a e f l m g h d j i n k o R je korjen stabla. R ima četiri podređena čvora ili nasljednika. Čvorovi c, f, g, h , i, k, l, m, n i o nemaju niti jedan nasljednik Korjen stabla R nalazi se na nultom nivou stabla. Nasljednici svih čvorova na i-tom nivou nalaze se na i+1 -om nivou. Prvi nasljednik nekog čvora v je onaj nasljednik w koji je naznačen (nacrtan) kao prvi nasljednik s lijeve strane crteža. Idući nasljednik istog nadređenog čvora v je prvi susjed čvora w. Npr. prvi nasljednik čvora b je čvor g. Prvi susjed čvora g je čvor h. Čvor i nema prvi susjed.

5. 1. 1 Prikaz i obilazak općeg stabla Povezani popis je jedan način prikaza. Svaki čvor prikazan je zapisom u povezanom popisu koji u podacima oznake nadređenog čvora, nasljednika i prvog susjeda. Pokazivač Idući pokazuje na naredni zapis. Čvor Nasljed- Susjed Idući nik Obilazak stabla je procedura kojom se stvara popis svih čvorova u stablu. Obilazak po širini je obilazak po nivoima i sličan je pretraživanju labirinta te također koristi red.

Algoritam obilaska općeg stabla po širini (pomoću reda) Staviti korjen u red Sve dok red nije prazan činiti Skinuti čvor iz red-a Ispisati čvor Ako postoji nasljednik činiti Ispisati nasljednik Staviti nasljednik u red Sve dok postoji susjed činiti Staviti susjed u red Ispisati susjed Kraj sve dok Kraj ako postoji nasljednik Kraj sve dok

5. 1. 2. Binarno stablo je stablo kod kojeg svaki čvor može imati najviše dva nasljednika. Oni su lijevi i desni nasljednik. Opće stablo može se prikazati binarnim stablom tako da za svaki čvor prvi nasljednik postane lijevi, a prvi susjed postane desni nasljednik u binarnom stablu. R Opće stablo s predhodne slike a postaje binarno stablo prikazano na slici na ovoj stranici. e b l f g c m d h i j n k o

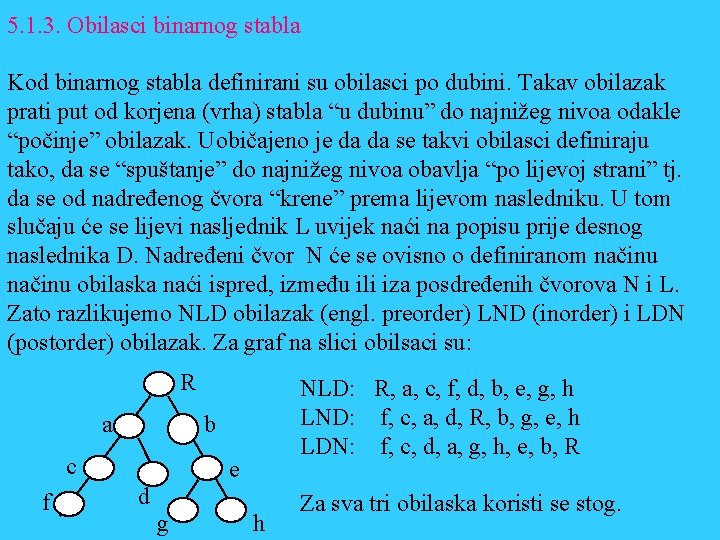
5. 1. 3. Obilasci binarnog stabla Kod binarnog stabla definirani su obilasci po dubini. Takav obilazak prati put od korjena (vrha) stabla “u dubinu” do najnižeg nivoa odakle “počinje” obilazak. Uobičajeno je da da se takvi obilasci definiraju tako, da se “spuštanje” do najnižeg nivoa obavlja “po lijevoj strani” tj. da se od nadređenog čvora “krene” prema lijevom nasledniku. U tom slučaju će se lijevi nasljednik L uvijek naći na popisu prije desnog naslednika D. Nadređeni čvor N će se ovisno o definiranom načinu obilaska naći ispred, između ili iza posdređenih čvorova N i L. Zato razlikujemo NLD obilazak (engl. preorder) LND (inorder) i LDN (postorder) obilazak. Za graf na slici obilsaci su: R a b c f NLD: R, a, c, f, d, b, e, g, h LND: f, c, a, d, R, b, g, e, h LDN: f, c, d, a, g, h, e, b, R e d g h Za sva tri obilaska koristi se stog.

5. 1. 3 Algoritam NLD obilaska Isprazniti stog Ispisati korjen stabla i staviti ga na stog Sve dok stog nije prazan činiti Sve dok cvor ima lijevi nasljednik činiti Postavit cvor=lijevi Staviti cvor na stog Ispisati cvor Kraj sve dok Sve dok cvor nema desni nasljednik i stog nije prazan činiti Skinuti cvor sa stoga Kraj sve dok Ako je stog prazan završiti obilazak Ispisati desni Staviti desni na stog Kraj sve dok

5. 1. 4. Algoritam LND obilaska Isprazniti stog i staviti “KRAJ” na stog Postavit cvor = korjen stabla Ponovljati Sve dok postoji lijevi nasljednik činiti Staviti cvor na stog Postaviti cvor=lijevi Kraj sve dok Postaviti desni_nas=0 Ponavljati Ispisati cvor Ako postoji desni nasljednik Postaviti cvor=desni nasljednik Postaviti desni_nas=1 U suprotnom skinuti cvor sa stog-a Dok je zadovoljen uvjet desni_nas=0 i stog nije prazan Dok je zadovoljen uvjet ima podataka na stog-u

5. 1. 5. Algoritam LDN obilaska Isprazniti stog Postaviti cvor=korjen stabla Ponavljati Sve dok postoji lijevi činiti Staviti cvor na stog Ako postoji desni staviti ga na stog s oznakom “D” Postaviti cvor=lijevi Kraj sve dok Staviti cvor na stog Ako postoji desni staviti ga na stog s oznakom”D” Postaviti desni_nas=0 Ponavljati Skinuti cvor sa stog-a Ako cvor ima oznaku “D” postavit desni_nas=1 U suprotnom ispisati cvor Do uvjeta prazan stog ili desni_nas=1 Do uvjeta prazan stog

5. 1. 6. Poredano binarno stablo (engl. Binary Search Tree) Ako su čvorovi binarnog stabla ozačeni međusobno usporedivim oznakama te je oznaka lijevog nasljednika manja a oznaka desnog nasljednika veća od oznake nadređenog čvora i to vrijedi za svaki čvor, takvo stablo se naziva poredano binarno stablo. Ovakvo binarno stablo omogućuje efikasno pretraživanje, dodavanje i brisanje. Algoritam pretraživanja treba pronaći da li se podatak P nalazi u stablu (oznaka jednog čvora je jednaka P), a ako se ne nalazi idikator nadjen poprima vrijednost -1. U oba slučaja nalazi se nadredjeni. Kada je P nađen, podatak nadredjeni dobiva oznaku čvora koji je nadređen traženom čvoru P. Ako P nije nađen (nadjen=-1) nadredjeni je čvor koji će biti nadređen ako se ubaci čvor P pri čemu će stablo i dalje ostati poredano binarno stablo.

Algoritam traženja “Trazi P” u poredanom binarnom stablu Učitati podatak P Postaviti cvor=korjen stabla Postaviti nadjen=0 Postaviti nadredjeni=0 Sve dok je nadjen=0 činiti Ako je cvor=P postaviti nadjen=1 U suprotnom činiti Postaviti nadredjeni=cvor Ako je P<cvor činiti Ako postoji lijevi postaviti cvor=lijevi U suprotnom postaviti nadjen=-1 Ako je P>cvor činiti Ako postoji desni postaviti cvor=desni U suprotnom postaviti nadjen=-1 Kraj sve dok

Algoritam “Dodaj P” dodavanja u poredano binarno stalo Algoritmom traženja “Nadji P” naći čvor P i njemu nadredjeni Ako je P nađen javiti da se čvor ne može dodati U suprotnom činiti Ako je P<nadredjeni dodaj P kao lijevi nasljednik od nadredjeni U suprotnom dodaj P kao desni nasljednik od nadredjeni Kraj u suprotnom

Algoritam “Brisi P” brisanja iz poredanog binarnog stabla Algoritmom traženja “Nadji P” naći čvor P i njemu nadredjeni Ako P nije nađen javiti da se čvor ne može brisati U suprotnom činiti Ako P nema desni nasljednik postaviti lijevi nasljednik na mjesto čvora P U suprotnom činiti Naći čvor Lndnas koji je LND nasljednika od desnog nasljednika čvora P Staviti Lndnas na mjesto čvora P Kraj u suprotnom

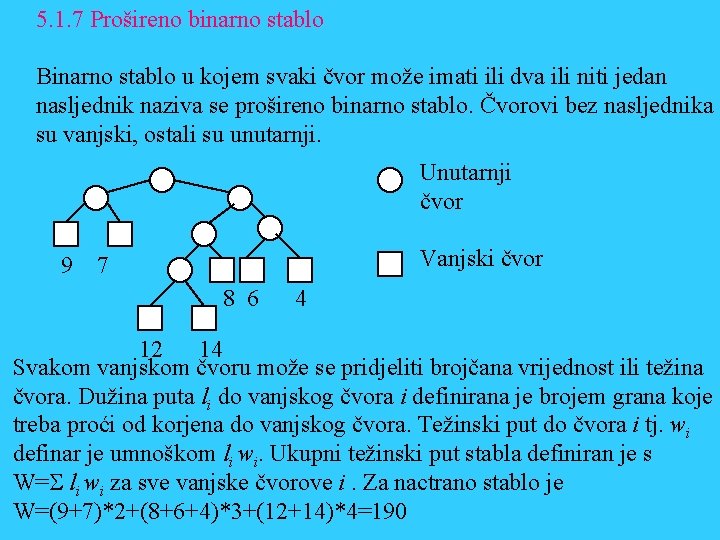
5. 1. 7 Prošireno binarno stablo Binarno stablo u kojem svaki čvor može imati ili dva ili niti jedan nasljednik naziva se prošireno binarno stablo. Čvorovi bez nasljednika su vanjski, ostali su unutarnji. Unutarnji čvor 9 Vanjski čvor 7 8 6 4 12 14 Svakom vanjskom čvoru može se pridjeliti brojčana vrijednost ili težina čvora. Dužina puta li do vanjskog čvora i definirana je brojem grana koje treba proći od korjena do vanjskog čvora. Težinski put do čvora i tj. wi definar je umnoškom li wi. Ukupni težinski put stabla definiran je s W=S li wi za sve vanjske čvorove i. Za nactrano stablo je W=(9+7)*2+(8+6+4)*3+(12+14)*4=190

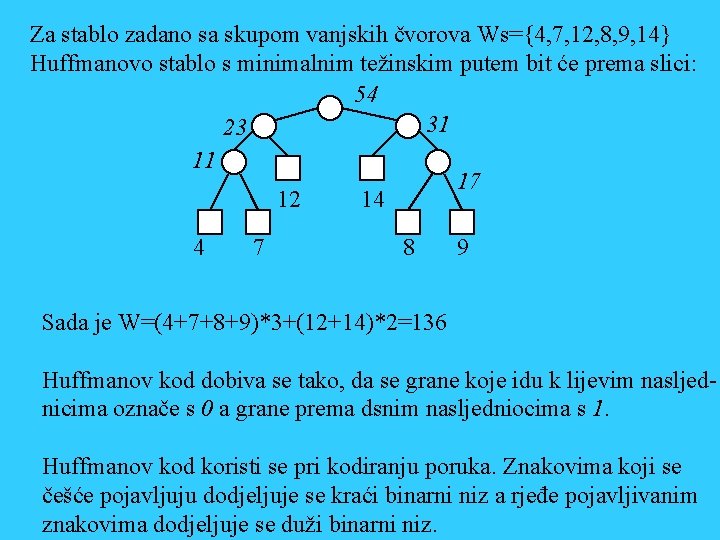
5. 1. 8 Huffmanovo stablo i Huffmanov algoritam Za zadane vanjske čvorove i njihove težine može se naći stablo s najmanjim težinskim putem tako da čvorovi s većom težinom dođu što bliže korjenu a čvorovi s malom težinom što dalje od korjena. To radi slijedeći Huffmanov algoritam Algoritam najmanjeg težinskog puta (Huffmanov algoritam) Težine čvorova wi staviti u skup Ws{wi} Sve dok je skup Ws neprazan činiti Naći dva najmanja elementa wmin 1 i wmin 2 u skupu Ws Ubaciti novi čvor stežinom wn= wmin 1 + wmin 2 u skup Ws Izbaciti čvorove wmin 1 i wmin 2 iz skupa Ws Kraj sve dok

Za stablo zadano sa skupom vanjskih čvorova Ws={4, 7, 12, 8, 9, 14} Huffmanovo stablo s minimalnim težinskim putem bit će prema slici: 54 31 23 11 12 4 7 17 14 8 9 Sada je W=(4+7+8+9)*3+(12+14)*2=136 Huffmanov kod dobiva se tako, da se grane koje idu k lijevim nasljednicima označe s 0 a grane prema dsnim nasljedniocima s 1. Huffmanov kod koristi se pri kodiranju poruka. Znakovima koji se češće pojavljuju dodjeljuje se kraći binarni niz a rjeđe pojavljivanim znakovima dodjeljuje se duži binarni niz.

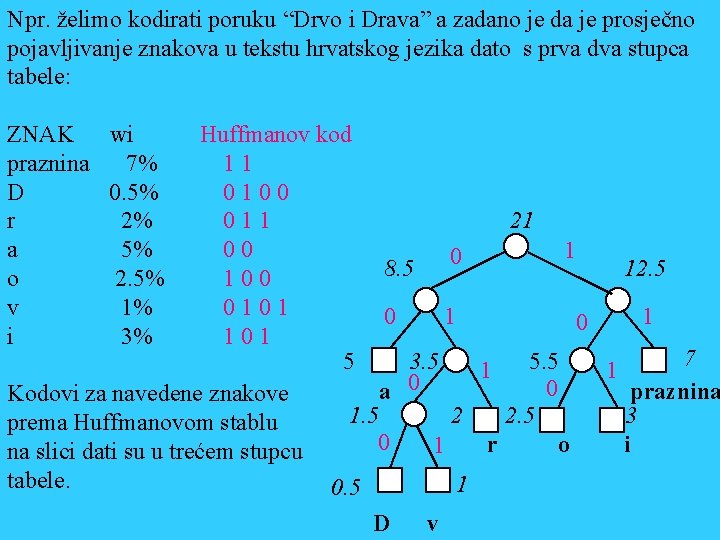
Npr. želimo kodirati poruku “Drvo i Drava” a zadano je da je prosječno pojavljivanje znakova u tekstu hrvatskog jezika dato s prva dva stupca tabele: ZNAK wi praznina 7% D 0. 5% r 2% a 5% o 2. 5% v 1% i 3% Huffmanov kod 11 0100 21 011 00 1 0 8. 5 12. 5 100 0101 0 101 7 5 3. 5 5. 5 1 1 0 a 0 praznina Kodovi za navedene znakove 1. 5 2 2. 5 3 prema Huffmanovom stablu 0 r o i 1 na slici dati su u trećem stupcu tabele. 1 0. 5 D v

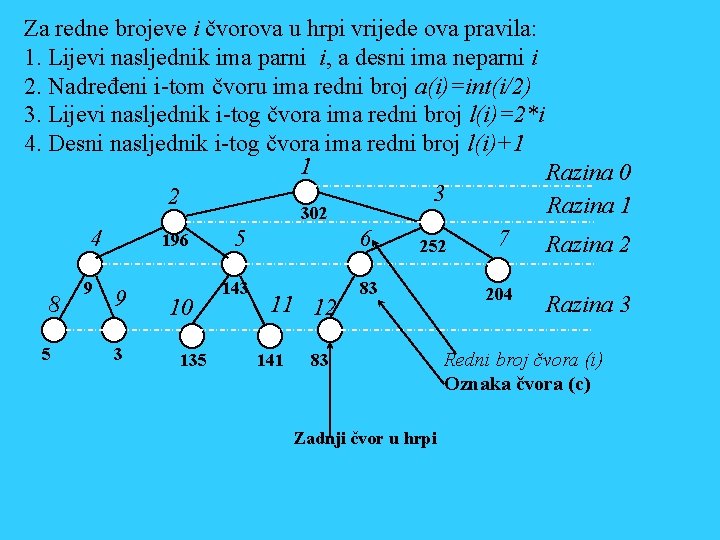
5. 1. 8. Potpuno binarno stablo i hrpa Stablo u kojem su sve razine popunjene a jedino posljednja razina ne mo biti popunjena zove se potpuno binarno stablo. Svaka ratina popunjava se s lijeva na desno. Ako je još zadovoljen uvjet, da je nadređeni čvor veći ili jednak od oba podređena, takvo potpuno binarno stablo zove se hrpa (engl. Heap). Ako se razina na kojoj je korjen stabla označi s 0 , onda na svakom popunjenoj razini n ima 2 n -tu čvorova (zadnja razina ne mora biti popunjen pa na tamo taj broj može biti i manji). Ako se čvorovima pridjele redni brojevi i={0. . N} (N je broj čvorova u stablu) s tim da numeracija ide od 0 -te ka većim razinama i od lijeva na desno onda se iz rednog broja i čvora može jednoznačno odrediti i redne brojeve njegovog prethodnika i oba nasljednika.

Za redne brojeve i čvorova u hrpi vrijede ova pravila: 1. Lijevi nasljednik ima parni i, a desni ima neparni i 2. Nadređeni i-tom čvoru ima redni broj a(i)=int(i/2) 3. Lijevi nasljednik i-tog čvora ima redni broj l(i)=2*i 4. Desni nasljednik i-tog čvora ima redni broj l(i)+1 1 Razina 0 3 2 Razina 1 302 4 8 5 9 196 9 3 10 135 5 6 143 83 11 12 141 252 83 Zadnji čvor u hrpi 7 Razina 2 204 Razina 3 Redni broj čvora (i) Oznaka čvora (c)

Algoritam “Dodaj u hrpu cvorx” (s povezanim popisom) Dodijeliti pokazivaču pc prvu slobodnu adresu Slogu na adresi pc postaviti lijevi=0; desni=0; cvor=cvorx; broj=ukupno_cvorova iduci=NULL Povečati ukupno_cvorova za 1 Ako je prvi=NULL postaviti prvi=pc U suprotnom činiti Postaviti ptr=prvi Postaviti broj_nadredjenog=ukupno_cvorova / 2 Sve dok je iduci na adresi ptr različit od NULL činiti Ako je broj_cvora na adresi ptr jednak broj_nadredjenog činiti Ako je ukupno_cvorova paran postaviti lijevi=cvor U suprotnom postaviti desni=cvor Kraj Ako je Kraj Sve dok je cvor>nadredjeni zamijeniti cvor i nadredjeni

Algoritam “Brisi iz hrpe cvorx” (s povezanim popisom) Naći zadnji čvor (s najvećim rednim brojem) Naći čvor cvorx koji treba brisati Zamijeniti čvorove zadnji i cvorx Sve dok je cvorx manji od svog lijevog ili desnog nasljednika činiti Zamijeniti cvorx s manjim nasljednikom Kraj sve dok Izbaciti cvorx iz povezanog popisa Smanjiti ukupno_cvorova za 1

Algoritam dodavanja u hrpu i brisanja iz hrpe: Hrpa je prikazana vektorom: Hrpa[0] =broj čvorova u hrpi Hrpa[i]=oznaka čvora s rednim brojem “i” Algoritam “Dodati cvor” Povećati Hrpa[0] za 1 Postaviti i=Hrpa[0] Postaviti Hrpa[i]=cvor Sve dok je Hrpa[i]<Hrpa[i/2] i i>1 činiti Zamijeniti Hrpa[i] i Hrpa[i/2] Podijeliti i s 2 Kraj sve dok

Algoritam “Brisati cvor” Naći i tako da je Hrpa[i]=cvor Postaviti j=Hrpa[0] Smanjiti Hrpa[0] za 1 Postaviti Hrpa[i]=Hrpa[j] Postaviti Hrpa[j]=0 Sve dok je Hrpa[i]<Hrpa[2*i] ili je Hrpa[i]<Hrpa[2*i+1] i Hrpa[2*i]>0 činiti /* Zamijeniti cvor s podređenim */ Ako je Hrpa[2*i]>Hrpa[2*i+1] činiti Zamijeniti Hrpa[2*i] s Hrpa[i] Pomnožiti i s 2 U suprotnom činiti Zamijeniti Hrpa[2*i+1] s Hrpa[i] Postaviti i=2*i+1 Kraj Ako je Kraj Sve dok

Sortiranje pomoću hrpe (Heap sort) Sve dok nije kraj podataka činiti Učitati broj Dodati broj u stablo Hrpa Kraj sve dok Sve dok Hrpa nije prazna činiti Ispisati korjen stabla Hrpa Brisati korjen iz stabla Hrpa Kraj sve dok

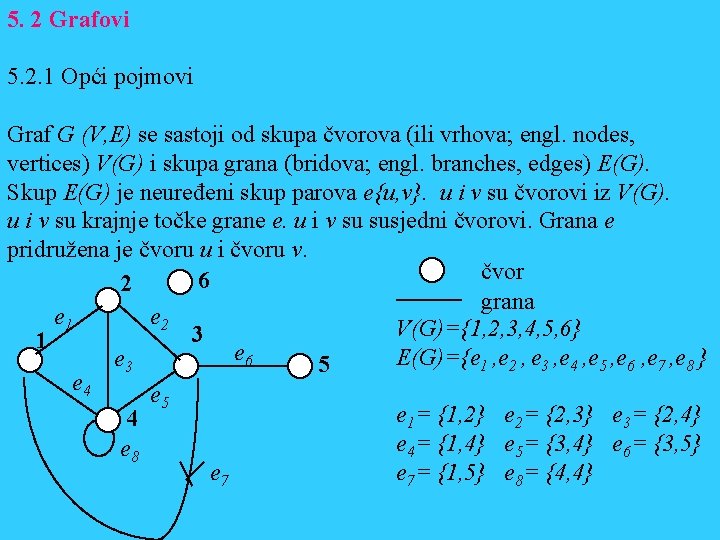
5. 2 Grafovi 5. 2. 1 Opći pojmovi Graf G (V, E) se sastoji od skupa čvorova (ili vrhova; engl. nodes, vertices) V(G) i skupa grana (bridova; engl. branches, edges) E(G). Skup E(G) je neuređeni skup parova e{u, v}. u i v su čvorovi iz V(G). u i v su krajnje točke grane e. u i v su susjedni čvorovi. Grana e pridružena je čvoru u i čvoru v. čvor 6 2 grana e 1 e 2 V(G)={1, 2, 3, 4, 5, 6} 3 1 e 6 E(G)={e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 } e 3 5 e 4 e 5 e 1= {1, 2} e 2= {2, 3} e 3= {2, 4} 4 e 4= {1, 4} e 5= {3, 4} e 6= {3, 5} e 8 e 7= {1, 5} e 8= {4, 4}

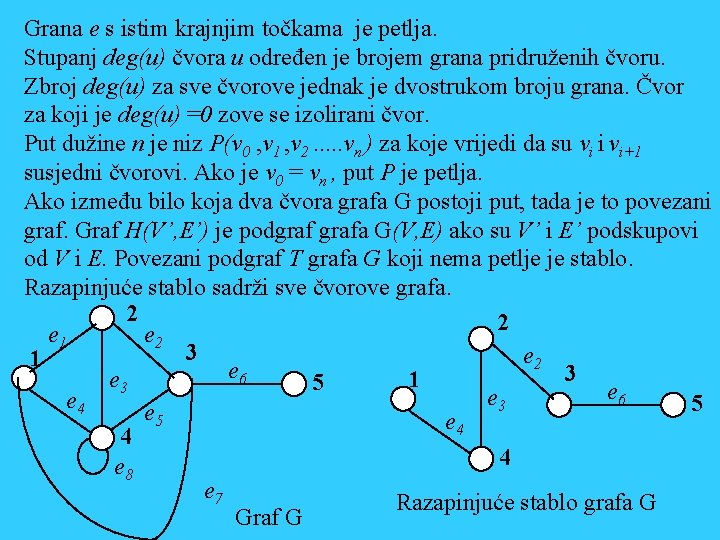
Grana e s istim krajnjim točkama je petlja. Stupanj deg(u) čvora u određen je brojem grana pridruženih čvoru. Zbroj deg(u) za sve čvorove jednak je dvostrukom broju grana. Čvor za koji je deg(u) =0 zove se izolirani čvor. Put dužine n je niz P(v 0 , v 1 , v 2. . . vn ) za koje vrijedi da su vi i vi+1 susjedni čvorovi. Ako je v 0 = vn , put P je petlja. Ako između bilo koja dva čvora grafa G postoji put, tada je to povezani graf. Graf H(V’, E’) je podgrafa G(V, E) ako su V’ i E’ podskupovi od V i E. Povezani podgraf T grafa G koji nema petlje je stablo. Razapinjuće stablo sadrži sve čvorove grafa. 2 2 e 1 e 2 3 e 2 1 e 6 3 e 3 1 5 e 6 e 3 e 4 5 e 4 4 4 e 8 e 7 Razapinjuće stablo grafa G Graf G

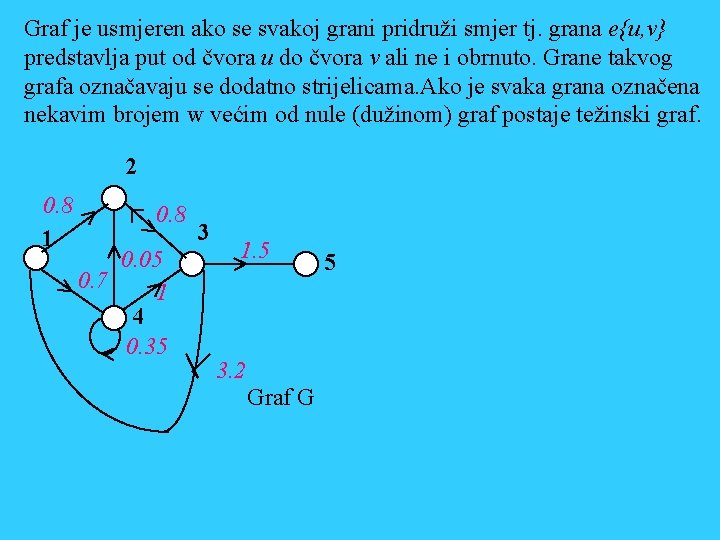
Graf je usmjeren ako se svakoj grani pridruži smjer tj. grana e{u, v} predstavlja put od čvora u do čvora v ali ne i obrnuto. Grane takvog grafa označavaju se dodatno strijelicama. Ako je svaka grana označena nekavim brojem w većim od nule (dužinom) graf postaje težinski graf. 2 0. 8 1 0. 8 0. 05 0. 7 1 4 0. 35 3 1. 5 3. 2 Graf G 5

5. 2. 2 Prikaz grafa u programu: Matrica susjedstva: S[i][j]=0 ako čvorovi i i j nisu susjedi S[i][j]=1 ako su čvorovi i i j susjedi Usmjereni graf G ima matricu susjedstva S prema slici 0 1 0 Matrica susjedstva je kvadratna i može se potencirati. 0 0 1 0 0 k-ta potencija te matrice daje broj puteva dužine k. S= 1 1 0 0 1 01110 00000 01210 23212 11001 01110 S 2= 0 1 1 1 0 S 3 = 1 2 2 1 1 S 4 = 12211 24322 00000 25432 12211 24322 37643 00000

5. 2. 3 Obilazak grafa je sastavljanje popisa svih čvorova; zadan je graf G(V, E), broj čvorova n i početni čvor c 0. Algoritma “Obilazak po širini” Za svaki i=0 do n-1 postaviti Status[i]=0 Staviti c 0 u Red Postaviti Status[c 0]=1 Sve dok Red nije prazan činiti Skinuti cvor iz reda Red Ispisati cvor Svaki susjed čvora cvor sa Status[susjed]=0 staviti u Red i postaviti Status[susjed]=1 Kraj sve dok Jednako tako obavlja se obilazak po dubini, samo se umjesto u red čvorovi stavljaju na stog.

5. 2. 4 Matrica povezanosti čvorova Iz matrice susjedstva S dobiva se u matrica povezanosti P u kojoj je P[i][j]=1 ako postoji put od čvora i do čvora j. U suprotnom P[i][j]=0. . Warshallov algoritam obavlja tu pretvorbu matrice S u matricu P. Za svaki i=0 do n-1 Za svaki j=0 do n-1 Postaviti P[i][j]=0 Za svaki k=0 do n-1 Za svaki i=0 do n-1 Za svaki j=0 do n-1 Ako je S[i][j]=1 ili S[i][k]=1 i S[k][j]=1 postaviti P[i][j]=1

Osim matrice susjedstva S za težinski graf definirana je i matrica težina W u kojoj je W[i][j]=wij tj. težina grane od i-tog do j-tog čvora. Za težinski graf G (s prethodne slike) matrica W ima vrijednosti NULL 0. 8 NULL 0. 7 NULL Ovdje NULL označava NULL 0. 8 NULL nepostojanje puta (put W= 3. 2 0. 8 NULL 1. 5 dužine beskonačno) NULL 0. 05 1. 0 0. 35 NULL NULL Modificirani Warshallov algoritam nalazi matricu najkraćih puteva Q među čvorovima. Za matricu Q koja je početno jednaka matrici W vrijedi Q[i][j]=min(Q[i][j], Q[i][k]+Q[k][j]

Modificirani Warshallov algoritam (algoritam najkraćeg puta) Zadana je matrica W s n redaka/stupaca Postaviti matrica Q= matrica W Za svaki k=0 do n-1 Za svaki i=0 do n-1 Za svaki j=0 do n-1 postaviti Q[i][j]=min(Q[i][j] , Q[i][k]+Q[k][j]) Za graf iz gornjeg primjera matrica najkraćih puteva Q je 4. 75 0. 75 4. 00 1. 60 Q= 3. 20 0. 80 4. 05 0. 05 NULL 1. 55 0. 70 3. 05 0. 80 4. 70 2. 30 1. 60 3. 90 1. 50 0. 85 0. 35 2. 35 NULL

5. 2. 5 Najkraći put između čvorova grafa i čvorove (i grane) na tom putu nalazi se algoritmom ”Najkraći put pretraživanjem po širini” (Napomena: Algoritam zahtjeva da su čvorovi označeni brojevima od 1 do n) Učitati broj čvorova n i matricu susjedstva S Učitati početni čvor pc i krajnji čvor kc Za svaki i=1 do n postaviti Status[i]=-2 Pozvati proceduru STABLO Pozvati proceduru ISPIS Procedura Stablo nalazi najkraće putove od početnog čvora pc do svih ostalih čvorova. Udaljenosti čvorova od početnog pc na putu stavljaju se u matricu Udaljenosti. i-ti red sadrži podatke za i-ti čvor. Prvi stupac (s indeksom 0) sadrži udaljenost, dok se u drugi stupac stavlja oznaka prethodnog čvora na putu. Iz te matrice procedura ISPIS ispisuje čvorove na najkraćem putu do kc-tog čvora iz kc-tog reda te matrice.

Algotitam “Stablo” Staviti pc u Red Postaviti Udaljenosti[pc][0]=0 i Udaljenosti[pc][1]=0 Sve dok Red nije prazan činiti U redu Red naći čvor cmin s najmanjom udaljenošću Za svaki susjed i čvora cmin koji ima Status[i]=-2 činiti Staviti čvor i u Red Naći u=Udaljenosti[cmin][1] + S[cmin][i] Ako je Status[i] =-2 ili u<Udaljenosti[i][1] činiti Postaviti Udaljenosti[i][0]=u Postaviti Udaljenosti[i][1]=cmin Postaviti Status[i]=0 U suprotnom postaviti Status[i]=-1 Kraj ako je Kraj za svaki susjed i Skinuti čvor cmin iz red Red Kraj sve dok

Algoritam procedure “ISPIS” Staviti kc na stog Postaviti prethodni_cvor=Udaljenosti[kc][1] Sve dok je Udaljenosti[prethodni_cvor][1] >0 činiti Staviti Udaljenosti[kc][1] na stog Postaviti prethodni_cvor=Udaljenosti[kc][1] Povećati i za 1 Kraj sve dok Sve dok se stog ne isprazni činiti Skinuti čvor sa stoga Ispisati čvor Kraj sve dok

Matrica Udaljenosti sadrži i krajnje čvorove grana u najmanjem razapinjućem stablu. Ispis tih čvorova postiže se procedurom ISPIS_NRS koja je nešto proširena gornja procedura ISPIS. Ispis se obavlja ne samo za čvor kc (koji ne mora biti niti zadan) već za sve krajnje čvorove stabla. To su čvorovi koji nisu prethodni čvorovi nit jednom čvoru stabla pa se ne nalaze u drugom stupcu (s indeksom 1) matrice Udaljenosti. Tim se čvorovima stavlja Status[i]=1 pa algoritam ISPIS_NRS je: Za svaki i=1 do n postaviti Status[i]=1 Za svaki i=1 do n činiti Postavit cvor=Udaljenosti[i][1] Postaviti Status[cvor]=0 Kraj za svaki i Za svaki i=1 do n Ako je Status[i]=1 pozvati proceduru ISPIS

6. Rekurzivne procedure 6. 1. Osnovni pojmovi Rekurzivne procedure ostvaruju se tako da se unutar neke procedure PROC obavi poziv te iste PROC procedure. Na primjer, faktorijel prirodnog broja definiran je s N!=N*(N-1)*(N-2)*. . . *2*1 ili N!=N*(N-1)! Algoritam NFAKT rekurzivne procedure NFAKT(n) će zato biti: Ako je n=1 vratiti 1 U suprotnom vratiti n*NFAKT(n-1) Općenito rekurzivna procedura ima najčešće gornji oblik tj. Ako je rješenje trivialno vratiti to rješenje U suprotnom obaviti rekurzivni poziv

6. 2 Quick sort rekurzijom Glavna procedura “QUICKSORT” Učitati n brojeva u vektor A Pozvati QUICK 1(0, n-1, A) Procedura QUICK 1(d, g, A) /* Poredati brojeve vektora A od d do g */ Ako je d>=g vratiti se u pozivajući program Postaviti m=QUICK 2(d, g, A) Pozvati QUICK 1(d, m-1, A) Pozvati QUICK 1(m+1, g, A)

Procedura QUICK 2(d, g, A) /* Naći indeks m tako da su brojevi lijevo manji od A[m] a desno veći */ Postaviti m=d Ako je d=g vratiti d Sve dok je A[g] > A[m] i m!=g smanjivati m za 1 Ako je m=g vratiti m Zamijeniti A[m] i A[g] Postaviti m=g Sve dok je A[d] A[m] i m!=d povećavati m za 1 Ako je m=d vratiti m Zamijeniti A[m] i A[g] Postaviti m=QUICK 2(d, g, A)

6. 3 Rekurzivno sortiranje ubacivanjem (Merge sort) Glavna procedura “MERGESORT” Učitati n brojeva u vektor A Pozvati SORT(0, n-1, A) Procedura SORT(d, g, A) Ako je d=g vratiti se u pozivajuću proceduru Pozvati SORT (d, (d+g) / 2, A) Pozvati SORT ((d+g)/2+1, g, A) Pozvati MERGE(d, g, A)

Procedura MERGE (d, g, A) Postaviti s=(d+g)/2, i 1=d i i 2=s+1 Za svaki i=0 do i=g-d činiti Ako je i 1<=s i i 2<= gg Ako je A[i 1]<A[i 2] činiti Postaviti T[i]=A[i 1] Povećati i 1 za 1 U suprotnom činiti Postaviti T[i]=A[i 2] Povećati i 2 za 1 U suprotnom Ako je i 1>s činiti Postaviti T[i]=A[i 2] Povećati i 2 za 1 U suprotnom činiti Postaviti T[i]=A[i 1] Povećati i 1 za 1 Za svaki i=d do g postaviti A[i]=T[i-d]

6. 4 Obilazasci binarnog stabla rekurzijom LND obilazak: procedura LND(cvor) Ako postoji lijevi pozovi LND(lijevi) Ispiši čvor cvor Ako postoji desni pozovi LND(desni) NLD obilazak: procedura NLD(cvor) Ispiši čvor cvor Ako postoji lijevi pozovi NLD(lijevi) Ako postoji desni pozovi NLD(desni) LDN obilazak: procedura LDN(cvor) Ako postoji lijevi pozovi LDN(lijevi) Ako postoji desni pozovi LDN(desni) Ispiši čvor cvor

6. 5 Elektromobil Zadatak: Vozilo s pogonom na bateriju (akumulator) s jednom baterijom prijeđe udaljenost k. Na raspolaganju je n baterija na početnom mjestu. Uz pogonsku bateriju vozilo ima mjesta za prijevoz još samo jedne baterije. Koliku udaljenost x može prijeći vozilo. Rješenje: d 2 d 1 xn xn-1 x 2=k x 1=k Vozilo prelazi udaljenost x prevozeći n-1 bateriju više puta (mora se i vraćati, osim kad prevozi zadnju). Zbog toga je k=2*(n-2)*x+x za n>1. Slijedi x=k/(2*n-3) Kako je d 1=k, d 2=x 2+d 1 općenito je dn =xn + dn-1 ili dn = k/(2*n-3)+ dn-1. Algoritam funkcije d(n, k) glasi Ako je n=1 vrati k U suprotnom vrati k/(2*n-3)+d(n-1)

6. 6 Algoritam “Osam kraljica” Zadatak: Na šahovsku ploću postaviti osam kraljica tako da se međusobno ne napadaju. Naći sva moguća rješenja. Rješenje: 1 1 Glavni program: Za svaki redak=1 do 8 Za svaki stupac= 1 do 8 Postaviti Ploca[redak][stupac]=0 Postaviti br_rjes=0 Pozvati proceduru Postavi(1) 8 * * * *

Procedura Postavi (redak) Za svaki j=1 do 8 činiti Ako je Ploca [redak][j]=0 činiti Pozvati proceduru Zauzmi(redak, j) Ako je redak=7 pozvati proceduru Ispis U suprotnom pozvati proceduru Postavi (redak+1) Pozvati proceduru Oslobodi(redak, j) Kraj ako je Kraj za svaki j

Procedura Zauzmi(redak, stupac) Za svaki i=1 do 8 povećati Ploca[i][stupac] za 1 Za svaki j=1 do 8 povećati Ploca[redak][j] za 1 Za svaki i=1 do 8 činiti Za svaki j=1 do 8 činiti Ako je i+j=redak+stupac ili je i- j=redak- stupac povećati Ploca[i][j] za 1 Kraj ako je Kraj za svaki j Kraj za svaki i Postaviti Ploca[redak][stupac]=9 Procedura Oslobodi(redak, stupac) vrlo je slična proceduri Zauzmi. Razlika je u tome što se obavlja smanjivanje za 1 (umjesto povećanja) broja u polju koje više ne napada skinuta kraljica. Također se na polje koje je bilo zauzeto kraljicom stavlja broj 0.

Procedura Ispis povećava broj rješenja za 1 i ispisuje matricu Ploca koja ima osam redaka i stupaca. Polje s brojem manjim od 9 ispisuje se kao “ “ (praznina), dok se polje s brojem 9 (polje na kojem je kraljica) prikazuje znakom “*”.