TANIM x 21 0 denkleminin gerel saylar kmesinde

TANIM: x 2+1 = 0 denkleminin gerçel sayılar kümesinde çözümü olmadığını biliyoruz. ( <0)

İ - SAYISININ KUVVETLERİ x 2 +1 = 0 denkleminde x 2 = -1

SONUÇ KALAN 0 1 2 3 ise ise 1 i -1 -i i 2

ÖRNEKLER 1) i 21 = ? 2) i 543 = ? 3) P(x) =

KARMAŞIK SAYILARIN STANDART BİÇİMİ Elemanları a +bi şeklinde olan kümeye karmaşık sayılar kümesi adı

ÖRNEKLER ve Im(z) = 0 1) z = 5 ise z = 5 +

KARMAŞIK SAYILARIN EŞİTLİĞİ İki karmaşık sayının karşılıklı olarak gerçel ve sanal kısımları kendi aralarında

KARMAŞIK SAYININ EŞLENİĞİ z = a+bi karmaşık sayısının eşleniği a-bi dir ve -z ile

KARMAŞIK SAYILAR KÜMESİNDE İŞLEMLER TOPLAMA-ÇIKARMA İki karmaşık sayının toplamında ve çıkarmasında, gerçel kısımlar kendi

ÇARPMA Normal çarpma işlemi yapılır. İşlem neticesinde i’nin kuvvetlerinin değeri bulunarak yerine konur. z

5) Çözüm kümesi {2 -5 i , 2+5 i} olan ikinci derece denklemi bulunuz?

KARMAŞIK DÜZLEM Analitik düzlemde x eksenini gerçel (reel) eksen, y-eksenini sanal (imajiner) eksen olarak

BİR KARMAŞIK SAYININ MUTLAK DEĞERİ Iz. I = I x+yi I = (x 2+y

4. z = x + y i karmaşık sayısı için z- z = -

KARMAŞIK DÜZLEMDE İKİ NOKTA ARASINDAKİ UZAKLIK Karmaşık düzlemde iki nokta arasındaki uzaklık; y 1

z 1= 2 -4 i ve z 2 = -4+4 i sayıları arasındaki uzaklık;

1. | z-z 0| = | z-(a+bi)| = r denklemi analitik düzlemde merkezi M(a,

5. z 0 =3+4 i ise A={z| z C ve |z- z 0|=3} kümesini

ÇIKARTMANIN GEOMETRİK GÖSTERİMİ z 1=a+bi nin görüntüsü A, z 2=c+di nin görüntüsü B, d

KARMAŞIK SAYININ KUTUPSAL (TRİGONOMETRİK) BİÇİMİ z=x+yi karmaşık sayısının düzlemdeki görüntüsü M(x, y) ve |OM|=r=|z|=

ARGÜMENT 0 o 2 olmak koşulu ile açısına z’nin esas argümenti denir. ve Arg(z)=

ÖRNEK: Yandaki z karmaşık sayısının kutupsal biçimi; r=|z|=6 ve =180 o-20 o=160 o olduğundan,

Slides: 24

Download presentation

TANIM: x 2+1 = 0 denkleminin gerçel sayılar kümesinde çözümü olmadığını biliyoruz. ( <0) x 2 +1 = 0 denkleminin çözülebildiği ve gerçel sayılar kümesini kapsayan daha geniş sayılar kümesi olan karmaşık sayılar kümesini oluşturacağız. Reel sayılar kümesinin kendisi ile çarpımı olan Rx. R kümesini C ile gösterelim. C = {a + bi ; a, b R ve i 2 = -1 } kümesine KARMAŞIK SAYILAR kümesi denir.

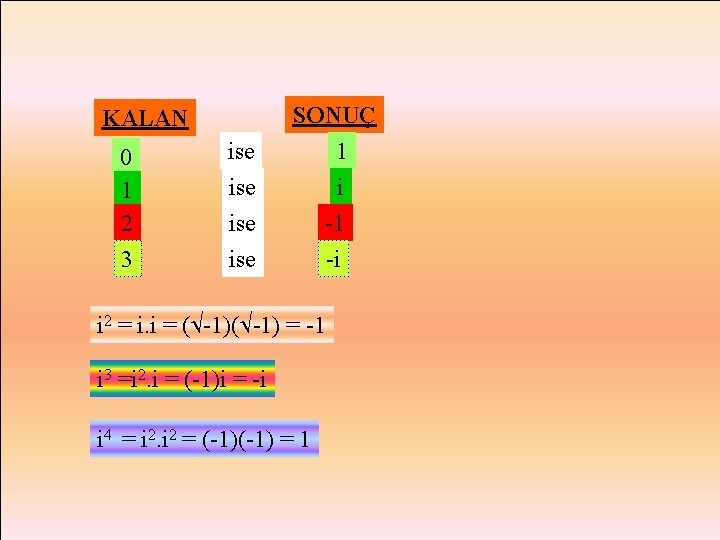
İ - SAYISININ KUVVETLERİ x 2 +1 = 0 denkleminde x 2 = -1 x = -1 olur. i = -1 alınırsa -5 = -1. 5 = i 5 -9 = 9. -1 = 3 i i sayısının herhangi bir kuvveti bulunurken kuvvetin 4 ile bölümündeki kalan i’nin kuvvetine yazılır.

SONUÇ KALAN 0 1 2 3 ise ise 1 i -1 -i i 2 = i. i = ( -1) = -1 i 3 =i 2. i = (-1)i = -i i 4 = i 2 = (-1) = 1

ÖRNEKLER 1) i 21 = ? 2) i 543 = ? 3) P(x) = 4 x 41 - 3 x 38 + 7 x 55 - 5 x 24 ise P(i) = ? 4) P(x) = x 3 + x - 1 olduğuna göre P( -4) = ?

KARMAŞIK SAYILARIN STANDART BİÇİMİ Elemanları a +bi şeklinde olan kümeye karmaşık sayılar kümesi adı verilir. C ile gösterilir. Her (a, b) karmaşık sayısı a+bi biçiminde yazılır ki bu yazılışa karmaşık sayının standart biçimi denir. z = a+bi şeklinde gösterilir. Herhangi bir z = a+bi karmaşık sayısında a reel sayısına z’nin gerçel (reel) kısmı , b reel sayısına da z’nin sanal (imajiner) kısmı denir. z = a+bi ise Re(z) = a ve Im(z) = b dir.

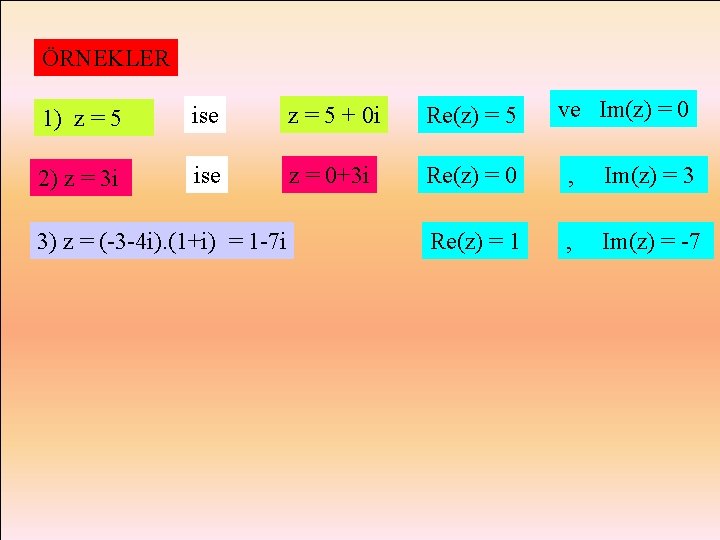
ÖRNEKLER ve Im(z) = 0 1) z = 5 ise z = 5 + 0 i Re(z) = 5 2) z = 3 i ise z = 0+3 i Re(z) = 0 , Im(z) = 3 Re(z) = 1 , Im(z) = -7 3) z = (-3 -4 i). (1+i) = 1 -7 i

KARMAŞIK SAYILARIN EŞİTLİĞİ İki karmaşık sayının karşılıklı olarak gerçel ve sanal kısımları kendi aralarında eşitse bu iki karmaşık sayı eşittir denir. z 1 = a+bi ve z 1 = z 2 = c+di karmaşık sayıları için; a = b ve c = d dir. ÖRNEKLER 1) z 1 = 2 x+3 i+y ve z 2 = xi+2+yi karmaşık sayıları eşit olduğuna göre (x, y) sayıları nedir? 2) 3 x+2 y+(2 x-y)i = 1 -4 i eşitliğini sağlayan x ve y sayılarını bulunuz. 3) 2 i+ 5 = 3 -2 xi+ 20. i-y ise x ve y’yi bulunuz.

KARMAŞIK SAYININ EŞLENİĞİ z = a+bi karmaşık sayısının eşleniği a-bi dir ve -z ile gösterilir. z = a+bi ise -z = a-bi ÖRNEKLER 1) z = 3+4 i ise z- = 3 -4 i 2) z = -2 -i ise z- = -2+i 3) z = 4 ise 4) z =-2 i ise z=4 z = 2 i

KARMAŞIK SAYILAR KÜMESİNDE İŞLEMLER TOPLAMA-ÇIKARMA İki karmaşık sayının toplamında ve çıkarmasında, gerçel kısımlar kendi aralarında, sanal kısımlar da kendi aralarında toplanır ve çıkarılır. z 1= a+bi ve z 2= c+di olsun. z 1+z 2 = (a+c)+(b+d)i z 1 - z 2 = z 1+(-z 2) = (a-c)+(b-d)i ÖRNEKLER 1) z 1 = 3 -2 i ve z 2 = -4+5 i ise z 1 + z 2 = ? 2) z 1 = -2+6 i ve z 1+z = -4 i ise z’nin eşiti nedir?

ÇARPMA Normal çarpma işlemi yapılır. İşlem neticesinde i’nin kuvvetlerinin değeri bulunarak yerine konur. z 1 = a+bi , z 2 = c+di olmak üzere; z 1. z 2 = (a+bi). (c+di) = (ac-bd)+(bc+ad)i ÖRNEKLER 1) z 1 = 2+3 i , z 2 = 4 -5 i ise z 1. z 2 = ? 2) z = (2 -7 i) ise z 2 sayısı nedir? 3) -5. -8. -10 = ? 4) (1+i)35 sayısını a+bi biçiminde yazınız.

5) Çözüm kümesi {2 -5 i , 2+5 i} olan ikinci derece denklemi bulunuz? BÖLME İki karmaşık sayının bölümünde pay ile paydanın eşleniği ile çarpılır. z 1 = a+bi ve z 2 = c+di ise z 1 = a+bi. c-di = (a+ib)(c+id) z 2 c+di c-di c 2+d 2 ÖRNEKLER 1) z 1 = 4+3 i , z 2 =3+2 i ise z 1/z 2 = ?

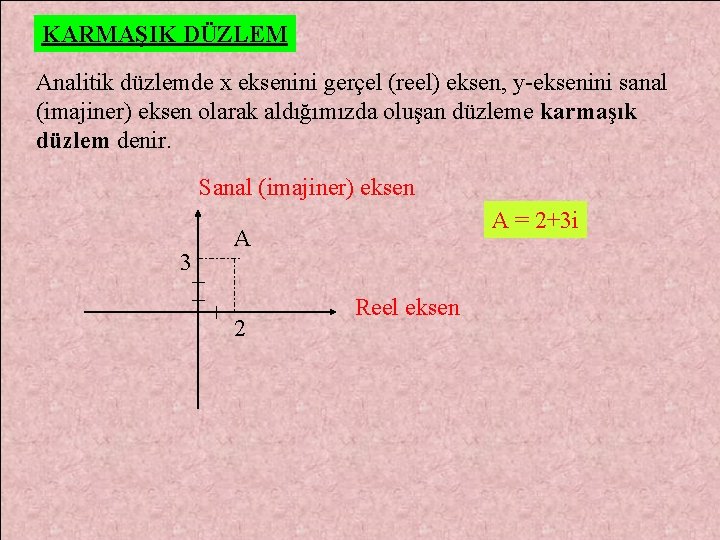
KARMAŞIK DÜZLEM Analitik düzlemde x eksenini gerçel (reel) eksen, y-eksenini sanal (imajiner) eksen olarak aldığımızda oluşan düzleme karmaşık düzlem denir. Sanal (imajiner) eksen 3 A = 2+3 i A 2 Reel eksen

BİR KARMAŞIK SAYININ MUTLAK DEĞERİ Iz. I = I x+yi I = (x 2+y 2) dir. Karmaşık düzlemde z = x+yi sayısına karşılık gelen noktanın orjine olan uzaklığına z karmaşık sayısının mutlak değeri (modülü) adı verilir. UYARI A=(x+yi) Iz. I O y x H 1. z C için Iz. I 0 2. Iz 1. z 2 I = Iz 1 I. Iz 2 I 3. z 1 z 2 Iz 1| = |z 2 I

4. zn = z n 5. z = - z 6. | 1/z| = 1 / |z| (z 0) 7. | | z 1| - | z 2| | | z 1 + z 2| | z 1| +| z 2| ÖRNEKLER 1. Aşağıdaki karmaşık sayıları düzlemde görüntüleyerek mutlak değerini bulunuz. B) z = - 5 i C) z= -3 A) z = 2 + 3 i 2. ( -2 + 3 i ) • ( 8 +6 i ) = ? 3. ( z 1 = 5 3 - 6 i , z 2 = 2 11 + 5 i , z 3 = 1 +2 2 i ise z 1 =? z 2 z 3

4. z = x + y i karmaşık sayısı için z- z = - 1 + 2 i ise z = ? 5. z, bir karmaşık sayı olmak üzere ; z - 2 i = i. z + 1 ise Im (z) = ?

KARMAŞIK DÜZLEMDE İKİ NOKTA ARASINDAKİ UZAKLIK Karmaşık düzlemde iki nokta arasındaki uzaklık; y 1 A y 2 z 1=x 1+y 1 i B x 1 z 2=x 2+y 2 i x 2 | z 1 -z 2 | = |AB| = (x 1 -x 2)2+(y 1 -y 2)2

1. | z-z 0| = | z-(a+bi)| = r denklemi analitik düzlemde merkezi M(a, b) ve yarıçapı r-olan çember denklemidir. 2. | z-z 0| = | z-(a+bi)| < r ifadesi merkezi (a, b), yarıçapı r olan çemberin iç bölgesidir. 3. |z-z 0| = | z-(a+bi)| > r ifadesi merkezi (a, b), yarıçapı r olan çemberin dış bölgesidir. ODAKLAYICI SORU: 1. {z| z C ve |z- (2+3 i)|=3}Kümesini karmaşık sayı düzleminde gösteriniz. 2. |z+1+i| 3 Kümesini karmaşık sayı düzleminde gösteriniz. 3. |z-i| > 3 Kümesini karmaşık sayı düzleminde gösteriniz. 4. |z+i| 2 Kümesini karmaşık sayı düzleminde gösteriniz.

5. z 0 =3+4 i ise A={z| z C ve |z- z 0|=3} kümesini karmaşık düzlemde gösteriniz 6. { z| z C ve |z+3 i| |z+6 -5 i| } kümesini karmaşık düzlemde gösteriniz. 7. x, y R olduğuna göre z=x+yi dir. 1 |z-1+i| 2 ifadesini karmaşık düzlemde gösteriniz. TOPLAMIN GEOMETRİK GÖSTERİMİ : z 1=a+bi z 1+z 2=(a+c)+(b+d)i z 2=c+di 0, z 1, z 2 ve z 1+z 2 bir parelel kenarın köşeleridir. d z 1+z 2 b z 1 ca

ÇIKARTMANIN GEOMETRİK GÖSTERİMİ z 1=a+bi nin görüntüsü A, z 2=c+di nin görüntüsü B, d -z 2=-c-di dir. z 1 - z 2=(a-c)+(b-d)i z 2 b c a 0, z 1, -z 2 ve z 1 - z 2 bir parelel kenarın köşeleridir. -z 2 z 1

KARMAŞIK SAYININ KUTUPSAL (TRİGONOMETRİK) BİÇİMİ z=x+yi karmaşık sayısının düzlemdeki görüntüsü M(x, y) ve |OM|=r=|z|= x 2+y 2 |z| =r M OMA ‘de x x=r. Cos , (x=|z|. Cos ) r y Sin = y=r. Sin , (y=|z|. Sin ) r z=x+yi 0 x y. A Cos = z=r. Cos +r. i. Sin = r(Cos +i. Sin )= r. Cis z=r(Cos +i. Sin ) veya z=r[Cos( +2 k )+i. Sin( +2 k )] , z=x+yi

ARGÜMENT 0 o 2 olmak koşulu ile açısına z’nin esas argümenti denir. ve Arg(z)= biçiminde yazılır. Arg( z )=Argz-1=2 -Argz z=x+yi karmaşık sayısının argümentinin esas ölçüsü bulunurken z=x+yi karmaşık düzlemde işaretlenerek hangi bölgede olduğu araştırılır. I. Bölgede ise Argz= II. Bölgede ise Argz= - III. Bölgede ise Argz= + IV. Bölgede ise Argz= 2 -

ÖRNEK: Yandaki z karmaşık sayısının kutupsal biçimi; r=|z|=6 ve =180 o-20 o=160 o olduğundan, y z 6 20 o z=6(Cos 160 o+i. Sin 160 o) dır. ODAKLAYICI SORU: 1 3 z i sayısının esas argümenti nedir ? = + 2 2 z= 2 2 - 2 2 i sayısının esas argümenti nedir ? z=1 - 3 i sayısını kutupsal biçimde yazınız. z = -3 2 +3 6 i ise (-z) sayısını kutupsal biçimde yazınız. z = -2 i sayısını kutupsal biçimde yazınız. eşitliğini sağlayan z karmaşık sayısının görüntülerini Arg(z+2)= 4 çiziniz. x