Takiniai ir intervaliniai veriai 2013 03 12 Paskaitos

Taškiniai ir intervaliniai įverčiai 2013 -03 -12

Paskaitos dalys Taškiniai ir intervaliniai įverčiai ¡ Iškeltų hipotezių tikrinimas ¡ Prognozavimas regresija ¡

Taškiniai ir intervaliniai įverčiai ¡ Taškiniai įverčiai Taškiniu regresijos parametro įverčiu vadiname pagal tam tikras taisykles apskaičiuotą įverčio skaitinę reikšmę. ¡ Pvz. MKM (porinės regresijos atveju)

Taškiniai įverčiai Porinės regresijos atveju ¡ Taškiniai įverčiai - atsitiktinis dydis l l Matematinė viltis E(b 0)= 0 , E(b 1)= 1 Dispersija

Taškinio įverčio standartinė paklaida Porinės regresijos atveju b 0 įverčio standartinė paklaida bj įverčio standartinė paklaida

DR įverčio b 0 dispersija ir standartinė paklaida Dispersija Įverčio b 0 standartinė paklaida

DR įverčio b 2 dispersija ir standartinė paklaida Dispersija Įverčio standartinė paklaida

DR įverčio b 1 dispersija ir standartinė paklaida Dispersija Įverčio standartinė paklaida

DR intervaliniai įverčiai Yi= 0+ 1 X 1 i+ 2 X 2 i. . . + I Yi=b 0+b 1 X 1 i+ b 2 x 2 i. . . +e. I Yra įrodoma, kad, jeigu tenkinama VI klasikinė regresijos prielaida, tuomet dydis

Intervaliniai iverčiai βj [bj koreguojantis dydis ] βj [bj tn-k-1, /2 SEbj]. ,

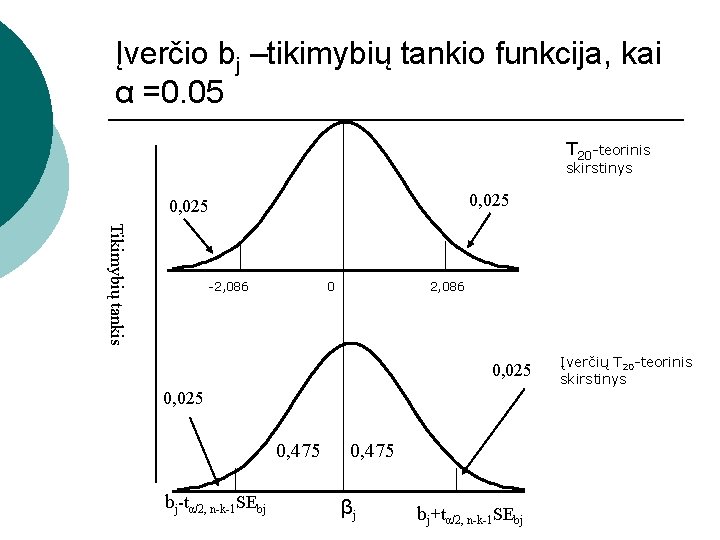
Įverčio bj –tikimybių tankio funkcija, kai α =0. 05 T 20 -teorinis skirstinys 0, 025 Tikimybių tankis -2, 086 0, 025 0, 475 bj-tα/2, n-k-1 SEbj 0, 475 βj bj+tα/2, n-k-1 SEbj Įverčių T 20 -teorinis skirstinys

Pvz. PVM regresijos lygtis ir pasikliautini intervalai βj [bj tn-k-1, /2 SEbj]. , tn-3, /2=t 40; 0. 025=2, 02

Iškeltų hipotezių tikrinimas ¡ Hipotezių tikrinimo procedūra l l Formuluojame hipotezę (H 0 ir H 1) Apskaičiuojama testo statistika Testo statistika lyginama su teorine skirstinio reikšme Daromos išvados

Hipotezių tikrinimas Parametrų statistinio reikšmingumo tikrinimas ¡ 1 žingsnis. Formuluojamos hipotezės: ¡ ¡ ¡ H 0 j = 0 (nepriklausomas kintamasis (Xj) nedaro įtakos priklausomam kintamajam t. y. , koeficientas prie veiksnio artimas 0) H 1 j ≠ 0 (Xj poveikis reikšmingas - regresijos koeficientas prie veiksnio nelygus 0) 2. žingsnis. Apskaičiuojama testo statistika. Veiksnių reikšmingumui tikrinti naudojama t statistika, kuri yra apskaičiuojama pagal formulę Dydis t yra pasiskirstęs pagal Stjudento t-skirstinį su /2 reikšmingumo lygmeniu ir n-k-1 laisvės laipsniais. t. y t~ t /2(n-k-1)

Hipotezių tikrinimas 3 žingsnis Apskaičiuota t statistikos reikšmė lyginama su teorine tskirstino t /2(n-k-1) reikšme. 4 žingsnis. Daromos išvados Jei apskaičiuota │t │ reikšmė yra didesnė už teorinę t-skirstinio reikšmę, tuomet nulinė hipotezė atmetama. Su 1 - tikimybe (pvz. , kai = 0, 05, t. y. , 1 - =0, 95 t. y. , 95 proc. tikimybe) galime tvirtinti, kad j-ojo veiksnio poveikis yra statistiškai reikšmingas. Priešingu atveju, kai │t │ apskaičiuota reikšmė yra mažesnė už teorinę reikšmę t /2(n-k-1), negalime atmesti nulinės hipotezės, o tai reiškia, kad negalime tvirtinti, kad j veiksnio poveikis yra statistiškai reikšmingas.

Parametrų statistinio reikšmingumo tikrinimo būdai Pasikliautini intervalai ¡ Teorinių ir faktinių T- skirstinio reikšmių palyginimas ¡ P- value reikšmė ¡

Vienpusės ir dvipusės hipotezės tikrinimo procedura Hipotezė Dvipusė H 0 –nulinė HAhipotezė alternatyvi hipotezė βj= β* βj ≠ β* Atmesti H 0 hipotezę It. I>tα/2, nk-1 Dešniašonė βj≤ β* βj > β* t>tα, , n-k-1 Kairiašonė βj≥ β* βj < β* t<-tα, , n-k-1

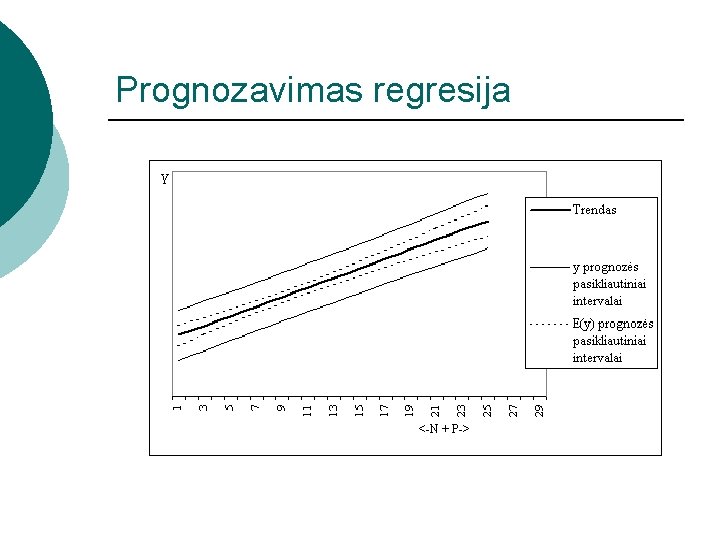
Prognozavimas regresija

Prognozavimas regresija E(Y) vidutinių prognozės pasikliautini intervalai Y reikšmių prognozės reikšmių pasikliautini intervalai