Steiner Tree Algorithms and Networks 20142015 Hans L

Steiner Tree Algorithms and Networks 2014/2015 Hans L. Bodlaender Johan M. M. van Rooij

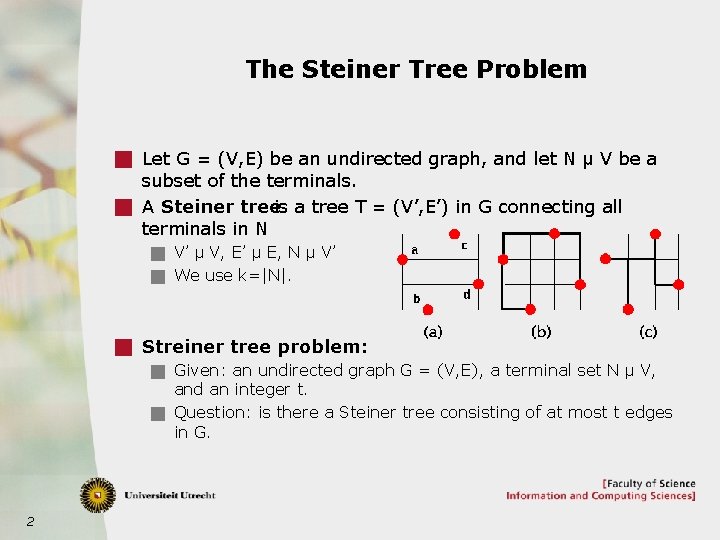
The Steiner Tree Problem g Let G = (V, E) be an undirected graph, and let N µ V be a subset of the terminals. g A Steiner treeis a tree T = (V’, E’) in G connecting all terminals in N g V’ µ V, E’ µ E, N µ V’ g We use k=|N|. g Streiner tree problem: g Given: an undirected graph G = (V, E), a terminal set N µ V, and an integer t. g Question: is there a Steiner tree consisting of at most t edges in G. 2

My Last Lecture g Steiner Tree. g Interesting problem that we have not seen yet. g Introduction g Variants / applications g NP-Completeness g Polynomial time solvable special cases. g Distance network. g Solving Steiner tree with k-terminals in O*(2 k)-time. g Uses inclusion/exclusion. g Algorithm invented by one of our former students. 3

Steiner Tree – Algorithms and Networks INTRODUCTION 4

Variants and Applications g Applications: g Wire routing of VLSI. g Customer’s bill for renting communication networks. g Other network design and facility location problems. g Some variants: g Vertices are points in the plane. g Vertex weights / edge weights vs unit weights. g Different variants for directed graphs. 5

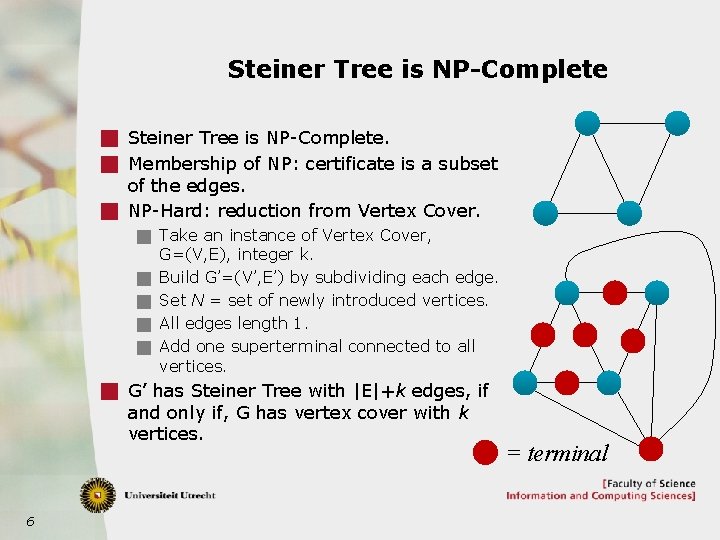
Steiner Tree is NP-Complete g Steiner Tree is NP-Complete. g Membership of NP: certificate is a subset of the edges. g NP-Hard: reduction from Vertex Cover. g Take an instance of Vertex Cover, g g G=(V, E), integer k. Build G’=(V’, E’) by subdividing each edge. Set N = set of newly introduced vertices. All edges length 1. Add one superterminal connected to all vertices. g G’ has Steiner Tree with |E|+k edges, if and only if, G has vertex cover with k vertices. 6 = terminal

Steiner Tree – Algorithms and Networks POLYNOMIAL-TIME SOLVABLE SPECIAL CASES 7

Special Cases of Steiner Tree g k = 1: trivial. g k = 2: shortest path. g k = n: minimum spanning tree. g k = c = O(1): constant number of terminals, polynomial- time solvable (next slides). 8

Distance Networks g Distance network D(X) of G=(V, E) (induced by the set X). g Take complete graph with vertex set X. g Cost of edge {v, w} in distance network is length shortest path from v to w in G. Observations: g Let W be the set of vertices of degree larger than two for an optimal Steiner tree T in G with terminal set N. g The Steiner tree T consists of a series of shortest paths between vertices in N [ W. g The cost of T equals the cost of the minimum spanning tree in D(N[W). g The cost of the optimal Steiner tree in D(V) equals the cost of T. 9

Steiner Tree with O(1) Terminals g Suppose |N|= k is constant c. g Compute distance network D(V). g There is a minimum cost Steiner tree in D(V) that contains at most k – 2 non-terminals. g Any Steiner tree that has one that is no longer without non- terminal vertices of degree 1 and 2. g A tree with r leaves and internal vertices of degree at least 3 has at most r – 2 internal vertices. g Polynomial time algorithm for k = O(1) terminals: g Enumerate all sets W of at most k – 2 non-terminals in G. g For each W, find a minimum spanning tree in the distance network D(NÈW). g Take the best over all these solutions g Takes polynomial time for fixed k = O(1). 10

Steiner Tree – Algorithms and Networks O*(2 K) ALGORITHM BY INCLUSION/EXCLUSION 11

Some background on the algorithm g Algorithm invented by Jesper Nederlof. g Just after he finished his Master thesis supervised by Hans (and a little bit by me). g Master thesis on Inclusion/Exclusion algorithms. 12

A Recap: Inclusion/Exclusion Formula g General form of the Inclusion/Exclusion formula: g Let N be a collection of objects (anything). g Let 1, 2, . . . , n be a series of requirements on objects. g Finally, let for a subset W µ {1, 2, . . . , n}, N(W) be the number of objects in N that do notsatisfy the requirements in W. g Then, the number of objects X that satisfy all requirements is: 13

The Inclusion/Exclusion formula: Alternative proofs g Various ways to prove the formula. 1. See the formula as a branching algorithm branching on a requirement: required = optional – forbidden 2. If an object satisfies all requirements, it is counted in N(Æ). If an object does not satisfy all requirements, say all but those in a set W’, then it is counted in all W µ W’ g With a +1 if W is even, and a -1 if W is odd. g W’ has equally many even as odd subsets: total contribution is 0. 14

Using the Inclusion/Exclusion Formula for Steiner Tree (problematic version) g One possible approach: g Objects: trees in the graph G. g Requirements: contain every terminal. g Then we need to compute 2 k times the number of trees in a subgraph of G. g For each W µ N, compute trees in G[VW]. g However, counting trees is difficult: g Hard to keep track of which vertices are already in the tree. g Compare to Hamiltonian Cycle: g We want something that looks like a walk, so that we do not need to remember where we have been. 15

Branching Walks g Definition: Branching walk in G=(V, E) is a tuple (T, Á): g Ordered tree T. g Mapping Á from nodes of T to nodes of G, s. t. for any edge {u, v} in the tree T we have that {Á(u), Á(v)} 2 E. g The length of a branching walk is the number of edges in T. g When r is the root of T, we say that the branching walk starts in Á(r) 2 V. g For any n 2 T, we say that the branching walk visits all vertices Á(n) 2 V. g Some examples on the blackboard. . . 16

Branching Walks and Steiner Tree g Definition: Branching walk in G=(V, E) is a tuple (T, Á): g Ordered tree T. g Mapping Á from nodes of T to nodes of G, s. t. for any edge {u, v} in the tree T we have that {Á(u), Á(v)} 2 E. g Lemma: Let s 2 N a terminal. There exists a Steiner tree T in G with at most c edges, if and only if, there exists a branching walk of length at most c starting in s visiting all terminals N. 17

Using the Inclusion/Exclusion Formula for Steiner Tree g Approach: g Objects: branching walks from some s 2 N of length c in the graph G. g Requirements: contain every terminal in N{s}. g We need to compute 2 k-1 times the number of branching walks of length c in a subgraph of G. g For each W µ N{s}, compute branching walks from s in G[VW]. g Next: how do we count branching walks? g Dynamic programming (similar to ordinary walks). 18

Counting Branching Walks g Let BW(v, j) be the number of branching walks of length j starting in v in G[W]. g BW(v, 0) = 1 for any vertex v. g BW(v, j) = u 2(N(v)ÅW) j BW(u, j 1) BW(v, j 2) 1 + j 2 = j-1 g j 2 = 0 covers the case where we do not branch / split up and walk to vertex u. g Otherwise, a subtree of size j 1 is created from neighbour u, while a new tree of size j 2 is added starting in v. This splits off one branch, and can be repeated to split of more branches. g We can compute BW(v, j) for j = 0, 1, 2, . . , t. g All in polynomial time. 19

Putting It All Together Algorithm: g Choose any s 2 N. g For t = 1, 2, … g Use the inclusion/exclusion formula to count the number of branching walks from s of length t visiting all terminals N. g This results in 2 k-1 times counting branching walks from s of length c in G[VW]. g If this number is non-zero: stop the algorithm and output that the smallest Steiner tree has size t. 20

Steiner Tree – Algorithms and Networks THAT’S ALL FOLKS… 21