STATISTIKA Numerike deskriptivne mere Prof dr Slaana Spasi

STATISTIKA Numeričke deskriptivne mere Prof. dr Slađana Spasić E-mail: sladjana. spasic@singidunum. ac. rs 2013. Beograd Predavanje 3

Numeričke deskriptivne mere Mere centralne tendencije podataka (srednje vrednosti ili proseci): aritmetička, geometrijska, harmonijska sredina • • Pozicione mere podataka: medijana, modus, kvartili, percentili • Mere disperzije podataka: interval varijacije, varijansa i standardna devijacija, koeficijent varijacije 2013. Beograd Predavanje 3 / 1

Mere centralne tendencije • Aritmetička sredina (prosek, srednja vrednost) skupa je broj koji se izračunava kada se zbir svih vrednosti numeričkog obeležja podeli sa ukupnim brojem tih vrednosti u skupu podataka. • Definicija: Srednja vrednost (µ) skupa od N elemenata: x 1, x 2, . . . , x. N , za posmatrano obeležje X je 2013. Beograd Predavanje 3 / 2

Mere centralne tendencije • Primer: Ako je na 5 tehničkih fakulteta broj upisanih studenata u prvu godinu studija bio 320, 360, 280, 450, 350 tada je prosečan broj upisanih u prvu godinu TF N = 5, 2013. Beograd Predavanje 3 / 3

Mere centralne tendencije • Aritmetička sredina uzorka se označava sa • Srednja vrednost uzorka od za posmatrano obeležje X je n elemenata: x 1, x 2, . . . , xn • Ovde je reč o aritmetičkoj sredini negrupisanih podataka. Svaki podatak se javlja samo jedanput. 2013. Beograd Predavanje 3 / 4

Mere centralne tendencije • Primer: Ako je uzmemo uzorak od 3 tehnička fakulteta, npr. u užoj Srbiji broj upisanih studenata u prvu godinu studija bio 360, 450, 350 tada je prosečan broj upisanih u prvu godinu TF n = 3, • Ali, ako je uzmemo uzorak od 2 tehnička fakulteta, izvan uže Srbije broj upisanih studenata u prvu godinu studija bio 320, 280 tada je prosečan broj upisanih u prvu godinu TF n = 2, Primetimo da je vrednost µ konstantna, dok se vrednost aritmetičke sredine uzorka razlikuje od uzorka do uzorka. Ona zavisi od vrednosti koje su uključene u uzorak. Posebno je osetljiva na ekstremne (najveće i najmanje) vrednosti i to joj je najveća mana. 2013. Beograd Predavanje 3 / 5

Aritmetička sredina grupisanih podataka • Neka su dati grupisani podaci u vidu tabele frekvencija sa k grupnih intervala, gde su x 1’, x 2’, . . . , xk’ njihove sredine, a f 1, f 2, . . . , fk odgovarajuće frekvencije grupnih intervala. • Aritmetička sredina grupisanih podataka ili ponderisana aritmetička sredina skupa je • Aritmetička sredina uzorka biće 2013. Beograd Predavanje 3 / 6

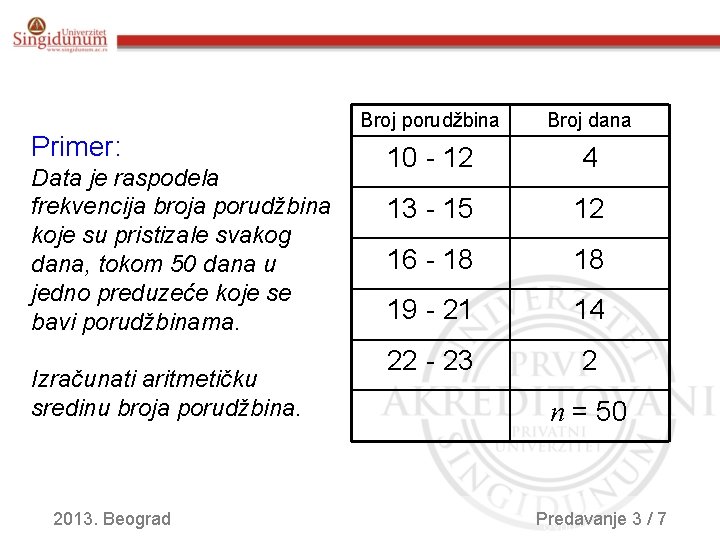
Primer: Data je raspodela frekvencija broja porudžbina koje su pristizale svakog dana, tokom 50 dana u jedno preduzeće koje se bavi porudžbinama. Izračunati aritmetičku sredinu broja porudžbina. 2013. Beograd Broj porudžbina Broj dana 10 - 12 4 13 - 15 12 16 - 18 18 19 - 21 14 22 - 23 2 n = 50 Predavanje /7 Uvod u teoriju 3 unformacija

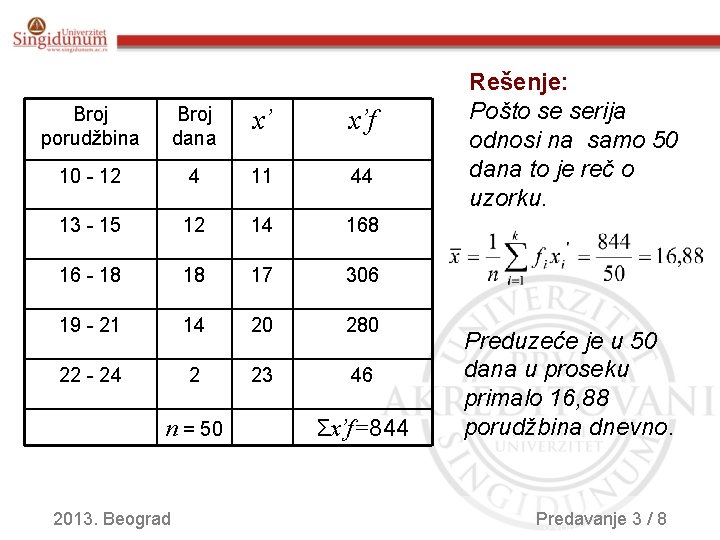
Broj porudžbina Broj dana x’ x’f 10 - 12 4 11 44 13 - 15 12 14 168 16 - 18 18 17 306 19 - 21 14 20 280 22 - 24 2 23 46 n = 50 2013. Beograd Σx’f=844 Rešenje: Pošto se serija odnosi na samo 50 dana to je reč o uzorku. Preduzeće je u 50 dana u proseku primalo 16, 88 porudžbina dnevno. Predavanje /8 Uvod u teoriju 3 unformacija

Osobine aritmetičke sredine 1. Aritmetička sredine veća je od najmanje, a manja od najveće vrednosti posmatranog obeležja: x 1<µ<xk 2. Ako je x 1=. . . =xk=a tada µ=a. 3. Zbir odstupanja aritmetičke sredine od vrednosti obeležja jednak je nuli: za negrupisane podatke za grupisane podatke 2013. Beograd Predavanje 3 / 9

Mere centralne tendencije • Geometrijska sredina izravnava relativne ili proporcionalne promene između vrednosti podataka (aritmetička sredina izravnava apsolutne vrednosti). Pogodna je za analize vremenskih serija. • Definicija: Geometrijska sredina (G) skupa od N elemenata: x 1, x 2, . . . , x. N , za posmatrano obeležje X je 2013. Beograd Predavanje 3 / 10

Mere centralne tendencije • Definicija: Neka je obeležje X dato sledećom raspodelom frekvencija: x 1, x 2, . . . , xk (> 0) su vrednosti obeležja X, a f 1, f 2, . . . , fk odgovarajuće frekvencije. Tada je geometrijska sredina (G) za posmatrano obeležje X Logaritmovanjem obe strane dobija se 2013. Beograd Predavanje 3 / 10

Mere centralne tendencije • Harmonijska sredina se koristi za analizu onih pojava kod kojih je njihov intenzitet obrnuto srazmeran vrednostima posmatranog obeležja. Pogodna je npr. za analizu produktivnosti u proizvodnji jer je produktivnost obrnuto proporcionalna vremenu potrebnom za proizvodnju nekog proizvoda. • Definicija: Harmonijska sredina (H) skupa od N elemenata: x 1, x 2, . . . , x. N , za posmatrano obeležje X je 2013. Beograd Predavanje 3 / 10

Košijeva teorema • Harmonijska sredina je manja od geometrijske, a geometrijska manja od artmetičke sredine, tj. važi: H<G<μ

Pozicione mere - medijana • Medijana se odnosi se na poziciju vrednosti u seriji, pa je zato poziciona mera. • Medijana je jednaka vrednosti središnjeg člana serije podataka koji su rangirani u rastućem poretku. Dakle, medijana deli grupisanu seriju podataka na dva jednaka dela, tako da prva polovina čini manje vrednosti od medijane, a druga veće. • Poređajmo seriju podataka od najmanjeg ka najvećem i pronađemo srednji član te serije. Vrednost tog člana će biti jednaka medijani ukoliko je broj članova neparan, a ukoliko je paran vrednost medijane će biti aritmetička sredina dva središnja podatka u seriji. 2013. Beograd Predavanje 3 / 11

Pozicione mere - medijana • Ako vrednosti obeležja X, od n elemenata, poređamo u neopadajući niz x 1≤ x 2 ≤. . . ≤ xn • Medijana ako je n neparan broj ako je n paran broj 2013. Beograd Predavanje 3 / 12

Pozicione mere - medijana • Primer: Ako su podaci o starosti profesora na fakultetu dati sa 56, 63, 46, 48, 42, onda je medijana 42, 46, 48, 56, 63 Ako su podaci o starosti profesora na fakultetu dati sa 56, 63, 46, 48, 42, 52 onda je medijana 42, 46, 48, 52, 56, 63 (48 + 52) / 2 = 50 2013. Beograd Predavanje 3 / 13

Pozicione mere - modus Modus je obeležje u seriji koje ima najveću frekvenciju pojavljivanja. Najčešće se javlja pa je najtipičnija vrednost u seriji. Serija može biti: • bez modusa (Primer: 12. 3, 23. 7, 14. 1, 67. 8, 34. 8) • unimodalna (sa jednim modusom) (Primer: Boja kose studenata iz grupe: plava, crna, smeđa, riđa, smeđa, crna, plava, smeđa; Mo=smeđa) • bimodalna (sa dva modusa) (Primer: Godine starosti studenata iz grupe: 19, 18, 19, 20, 18. 5, 20, 19; Mo su 19 i 20 jer se javljaju po 4 puta) • multimodalna (sa više modusa) 2013. Beograd Predavanje 3 / 14

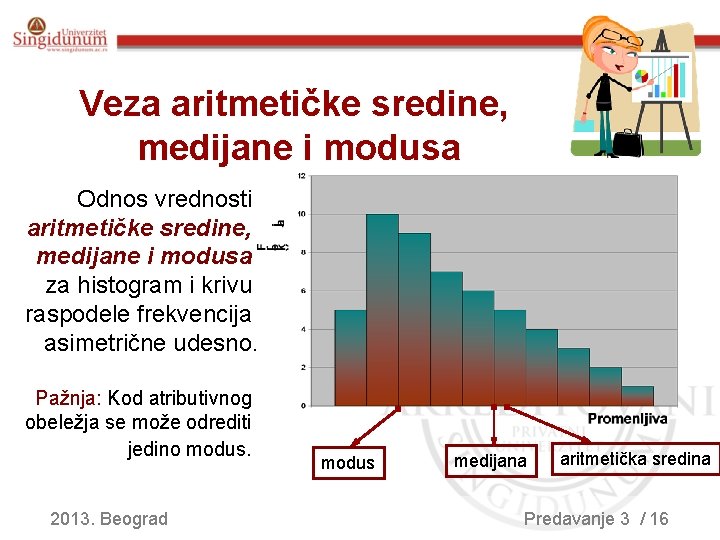
Veza aritmetičke sredine, medijane i modusa Vrednosti aritmetičke sredine, medijane i modusa za simetričan histogram i simetričnu krivu raspodele frekvencija se poklapaju. aritmetička sredina = medijana = modus 2013. Beograd Predavanje 3 / 15

Veza aritmetičke sredine, medijane i modusa Odnos vrednosti aritmetičke sredine, medijane i modusa za histogram i krivu raspodele frekvencija asimetrične udesno. Pažnja: Kod atributivnog obeležja se može odrediti jedino modus. 2013. Beograd modus medijana aritmetička sredina Predavanje 3 / 16

Mere disperzije negrupisanih podataka Ø Mere centralne tendencije, kao što su aritmetička sredina, medijana i modus, ne objašnjavaju u potpunosti raspodelu određene serije podataka. Ø Dve serije podataka sa istom aritmetičkom sredinom mogu imati potpuno različite raspodele frekvencije, tj. njihova raspršenost može biti potpuno različita. 2013. Beograd Predavanje 3 / 17

Mere disperzije negrupisanih podataka • Disperzija, raspršenost, ili rasturanje podataka • Mere disperzije ukazuju na raspršenost raspodele. • To su: – Interval varijacije – Varijansa – Standardna devijacija – Koeficijent varijacije 2013. Beograd Predavanje 3 / 18

Mere disperzije negrupisanih podataka Interval varijacije je mera raspršenosti koja je jednaka razlici najveće i najmanje vrednosti u seriji podataka: i = xmax-xmin Varijansa skupa je Čita se: Sigma na kvadrat ! Varijansa uzorka je Standardna devijacija skupa (uzorka) je pozitivni kvadratni koren varijanse skupa (uzorka). Koeficijent varijacije je je odnos standardne devijacije i aritmetičke sredine tj. V=σ/µ 2013. Beograd Predavanje 3 / 19

Radne formule i osobine Varijansa skupa je Varijansa uzorka je Standardna devijacija skupa Standardna devijacija uzorka Varijansa i standardna devijacija su uvek nenegativne (≥ 0). Varijansa = 0 akko x 1= x 2= …= x. N = const. Koeficijent varijacije = 0 akko x 1= x 2= …= x. N = const. 2013. Beograd Predavanje 3 / 20

Mere disperzije Primer: Izračunati interval varijacije, koeficijent varijacije, varijansu i standardnu devijaciju za skup: 5, -7, 2, 0, -9, 16, 10, 7. N =8 i = xmax-xmin = 16 - (-9) = 25 2013. Beograd xi -9 -7 0 2 5 7 10 16 576 x i 2 81 49 0 4 25 49 100 256 564 Predavanje 3 / 21

Mere disperzije Primer: Izračunati interval varijacije, koeficijent varijacije, varijansu i standardnu devijaciju za uzorak: 14, 18, -10, 8, 8, -16. xi x i 2 n =6 i = xmax-xmin = 18 - (-16) = 34 2013. Beograd -16 -10 8 8 14 18 484 256 100 64 64 196 326 1006 Predavanje 3 / 22

Mere disperzije grupisanih podataka Varijansa grupisanog skupa je Varijansa grupisanog uzorka je gde je σ 2 varijansa skupa, s 2 varijansa uzorka, xi’ sredina intervala. 2013 Beograd Predavanje 3 / 23

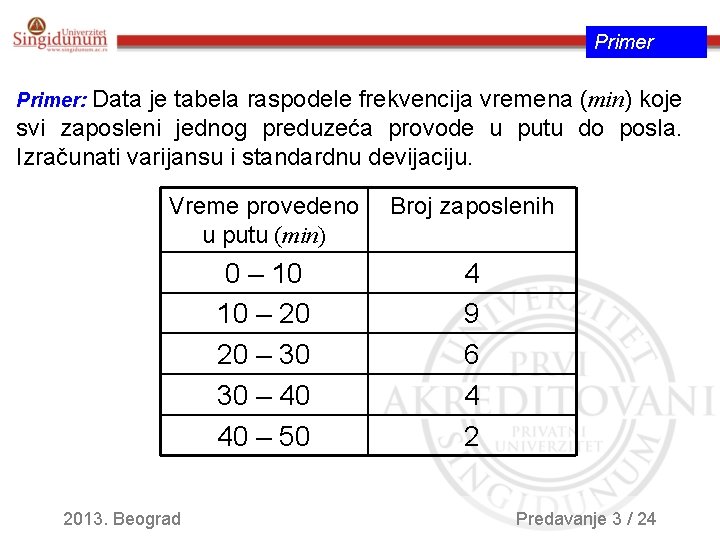
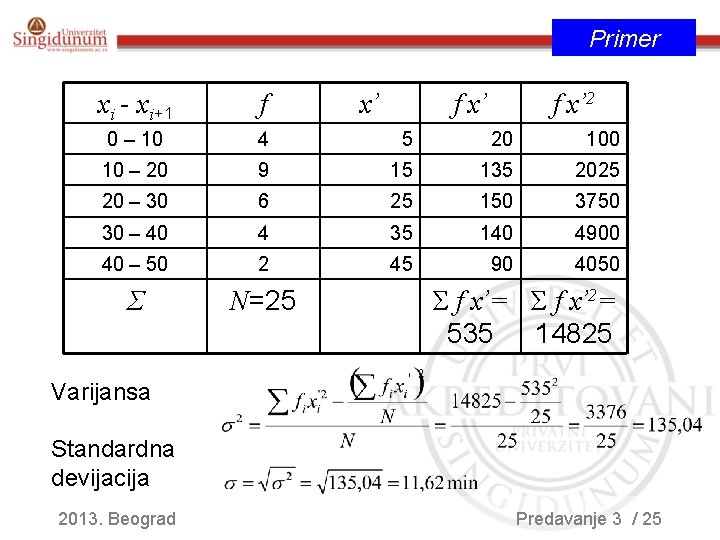
Primer: Data je tabela raspodele frekvencija vremena (min) koje svi zaposleni jednog preduzeća provode u putu do posla. Izračunati varijansu i standardnu devijaciju. Vreme provedeno u putu (min) Broj zaposlenih 0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 4 9 6 4 2 2013. Beograd Predavanje 3 / 24

Primer xi - xi+1 f 0 – 10 4 5 20 10 – 20 9 15 135 2025 20 – 30 6 25 150 3750 30 – 40 4 35 140 4900 40 – 50 2 45 90 4050 Σ N=25 x’ f x’ 2 Σ f x’= Σ f x’ 2= 535 14825 Varijansa Standardna devijacija 2013. Beograd Predavanje 3 / 25

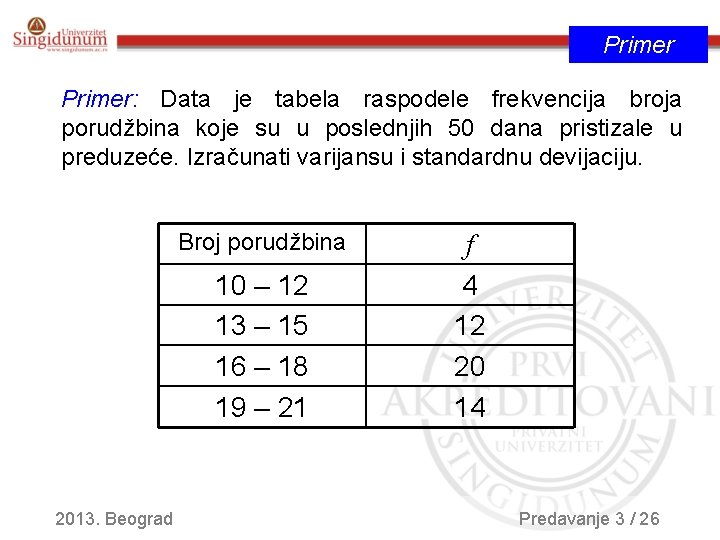
Primer: Data je tabela raspodele frekvencija broja porudžbina koje su u poslednjih 50 dana pristizale u preduzeće. Izračunati varijansu i standardnu devijaciju. Broj porudžbina 10 – 12 13 – 15 16 – 18 19 – 21 2013. Beograd f 4 12 20 14 Predavanje 3 / 26

Primer xi - xi+1 f x’ 10 – 12 4 11 44 484 13 – 15 12 14 168 2352 16 – 18 20 17 340 5780 19 – 21 14 20 280 5600 Σ n =50 f x’ 2 Σ f x’= Σ f x’ 2= 14216 832 Varijansa Standardna devijacija 2013. Beograd Predavanje 3 / 27

Parametri osnovnog skupa i statistike uzorka Numeričke mere kao što su aritmetička sredina, medijana, modus, interval varijacije, varijansa i standardna devijacija koje su izračunate za osnovni skup zovu se parametri skupa ili samo parametri. Deskriptivna mera koja se izračunava na uzorku naziva se statistika uzorka ili statistika. 2013. Beograd Predavanje 3 / 28

Osnovni skup Parametri µ σ2 σ 2013. Beograd Uzorak Statistike s 2 s Predavanje 3 / 29

Pozicione mere podataka • Pozicione mere podataka (medijana, modus, kvartili, percentili) • Kvartili su tri deskriptivne mere Q 1, Q 2, Q 3 koje dele rangiranu seriju podataka na četiri jednaka dela. • Interkvartilna razlika je 25% xmin i q= Q 3 - Q 1 25% Q 1 prvi kvartil 2013. Beograd 25% Q 2 =Me drugi kvartil 25% Q 3 xmax treći kvartil Predavanje 3 / 30

Pozicione mere podataka • Percentili su deskriptivne mere koje dele seriju podataka rangiranu po veličini na 100 jednakih delova. • Ima ih 99 : P 1, P 2, . . . , P 98, P 99 1% xmin 1% P 1 prvi prcentil 2013. Beograd . . . P 2 drugi percentil 1% P 99 99 -ti percentil xmax Predavanje 3 / 31

Podsećanje Numeričke deskriptivne mere • Mere centralne tendencije podataka (aritmetička, geometrijska, harmonijska sredina) • Mere disperzije podataka (interval varijacije, koeficijent varijacije, varijansa i standardna devijacija) • Pozicione mere podataka (medijana, modus, kvartili, percentili) 2013. Beograd Predavanje 3 / 32