Sonar Equation Parameters determined by the Medium Transmission

Sonar Equation Parameters determined by the Medium • Transmission Loss TL • spreading • absorption • Reverberation Level RL (directional, DI can’t improve behaviour) • Ambient-Noise Level NL (isotropic, DI improves behaviour) Parameters determined by the Equipment • Source Level SL • Self-Noise Level NL • Receiver Directivity Index DI • Detector Threshold DT (not independent) Parameters determined by the Target • Target Strength • Target Source Level TS SL 1 Oc 679 Acoustical Oceanography

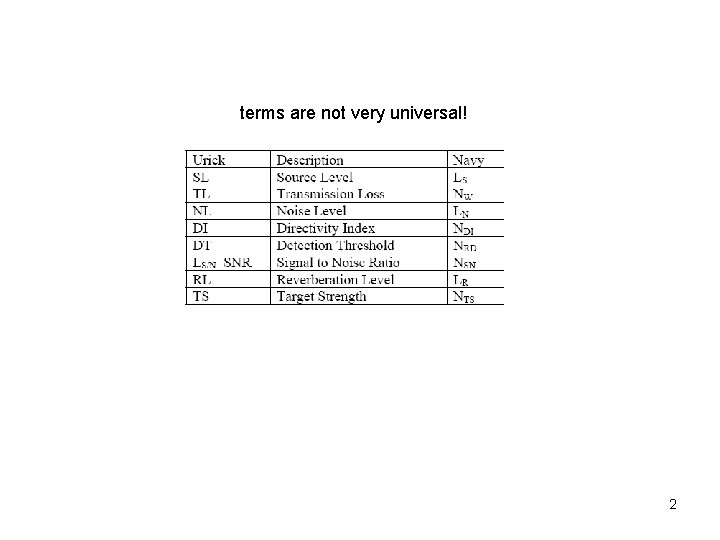
terms are not very universal! 2

Units N = 10 log 10 where I 0 is a reference intensity the unit of N is deci. Bels so we might say that I and I 0 differ by N d. B in terms of acoustic pressure, (p/p 0)2 I/I 0 where the oceanographic standard is p 0 = 1 Pa in water we can write this in terms of pressure as 20 log 10 for comparison: • atmospheric pressure is 100 k. Pa • pressure increases at the rate of 10 k. Pa per meter of depth from the surface down p/p 0 d. B = 20 log 10 p/p 0 1 √ 2 2 4 10 20 1000 0 3 (double power level) 6 12 compare p/p 0=1/√ 2, I/I 0 = ½ 20 d. B = -3 26 we might say the -3 d. B level or ½ power level 40 60 3 Oc 679 Acoustical Oceanography

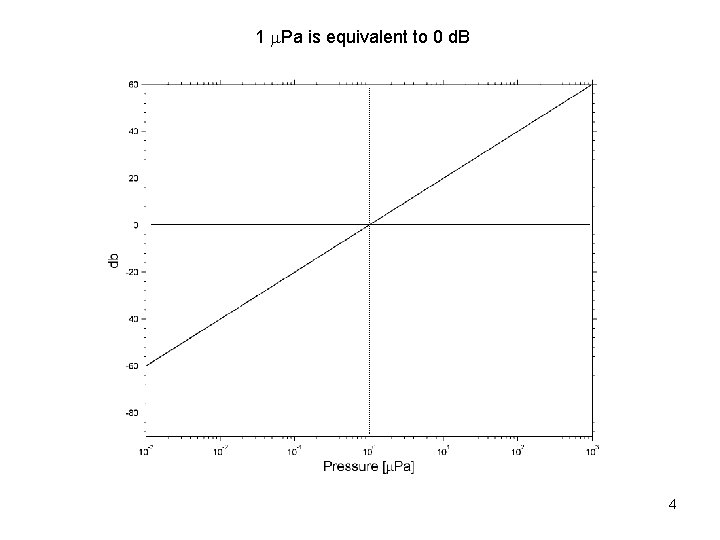
1 Pa is equivalent to 0 d. B 4

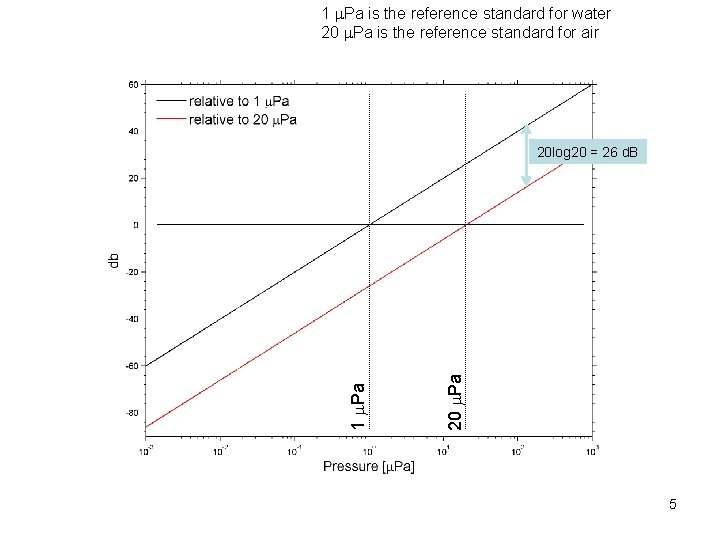
1 Pa is the reference standard for water 20 Pa is the reference standard for air 20 Pa 1 Pa 20 log 20 = 26 d. B 5

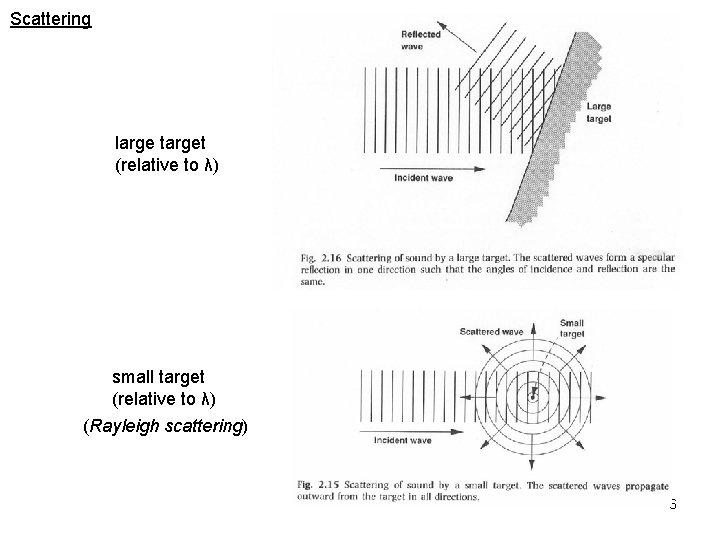
Scattering large target (relative to λ) small target (relative to λ) (Rayleigh scattering) 6

Scattering scattering of light follows essentially the same scattering laws as sound but light wavelengths are much smaller than sound - O(100 s of nm) almost all scattering bodies in seawater are large compared to optical wavelengths and have optical cross-sections equal to their geometrical cross-sections Large Targets the sea is turbid to light on the other hand, acoustic wavelengths are typically large compared to scattering bodies found in seawater (at 300 k. Hz, 5 mm, 4 orders of magnitude larger) - acoustic scattering is dominated by Rayleigh scattering Small Targets by comparison the sea is transparent to sound - what limits the propagation of 300 k. Hz sound is not scattering but absorption 7

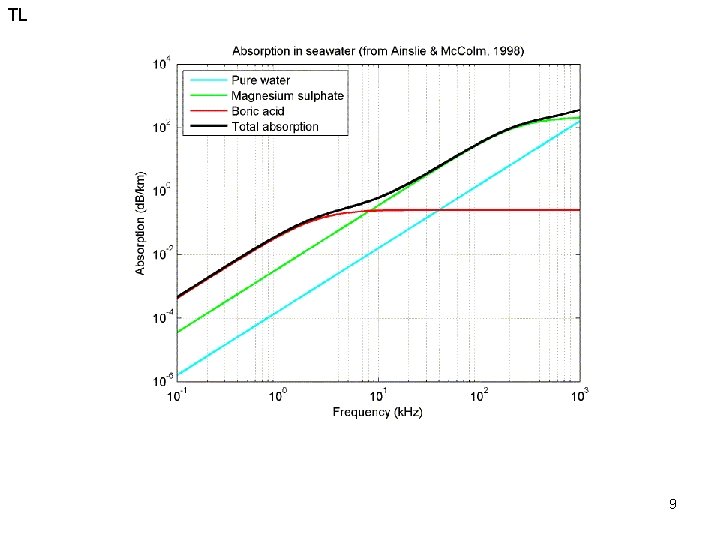
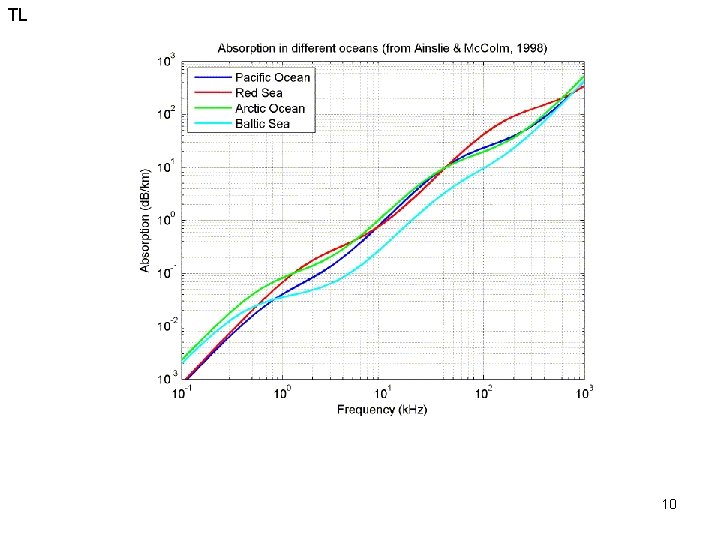
TL Absorption in a homogeneous medium, a plane wave experiences an attenuation of acoustic pressure the original pressure and to the distance traveled – this is represented by a bulk viscosity in the N-S equations which applies only to compressible fluid (this is distinct from a shear viscosity – M&C sec 3. 4. 2) this is due To wave absorption (energy lost to heat) e is the amplitude decay coefficient absorption losses are due to ionic dissociation that is alternately activated and deactivated by sound condensation and rarefaction • the attenuation by this manner in SW is 30 x that in FW • dominated by magnesium sulphate and boric acid acoustic absorption frequency @S=0 3000 k. Hz 1500 k. Hz 2. 4 d. B/m 0. 60 d. B/m 0. 07 d. B/m absorption @S=35 2. 5 d. B/m 0. 67 d. B/m 0. 14 d. B/m typical profiling range 3 -6 m 15 -25 m 70 -110 m source: Sontek ADCP manual 8 Oc 679 Acoustical Oceanography

TL 9

TL 10

TL relate spherical spreading & range attenuation due to absorption in terms of sonar equation spherical spreading 1/R 2, that is log 10 I/I 0 = log 10 R 02/R 2 = log 10 R 02 – log 10 R 2 but since typically I 0 is referred to 1 m range from source, log 10 R 02=0 and 10 log 10 I/I 0 = – 20 log 10 R range attenuation related by p = p 0 e- R, or I = I 0 e-2 R then 10 log 10 I/I 0 = - 20 R and together these represent a transmission loss TL = -20 log 10 R - 20 R absorption spherical spreading 11 Oc 679 Acoustical Oceanography

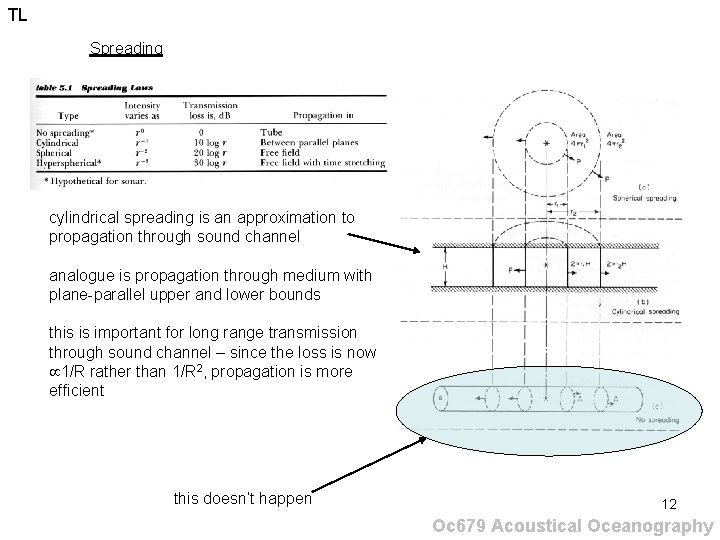
TL Spreading cylindrical spreading is an approximation to propagation through sound channel analogue is propagation through medium with plane-parallel upper and lower bounds this is important for long range transmission through sound channel – since the loss is now 1/R rather than 1/R 2, propagation is more efficient this doesn’t happen 12 Oc 679 Acoustical Oceanography

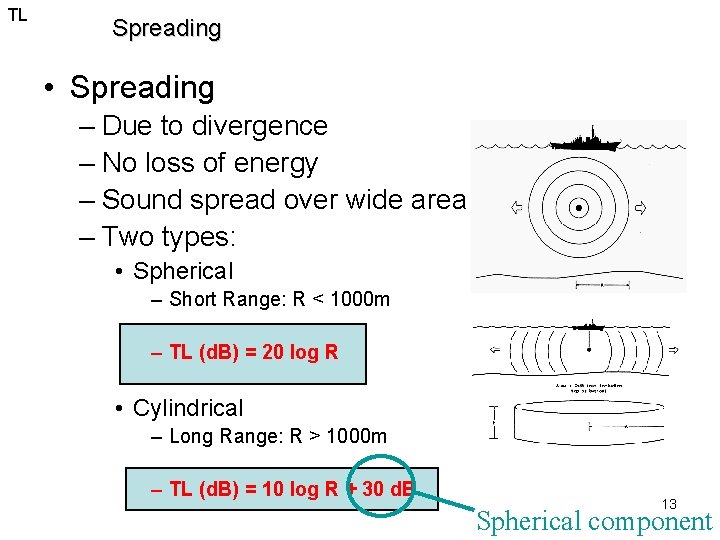
TL Spreading • Spreading – Due to divergence – No loss of energy – Sound spread over wide area – Two types: • Spherical – Short Range: R < 1000 m – TL (d. B) = 20 log R • Cylindrical – Long Range: R > 1000 m – TL (d. B) = 10 log R + 30 d. B 13 Spherical component

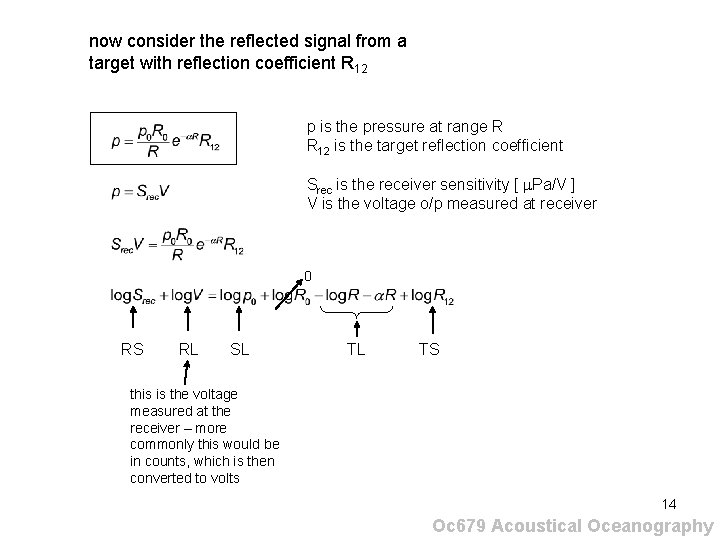
now consider the reflected signal from a target with reflection coefficient R 12 p is the pressure at range R R 12 is the target reflection coefficient Srec is the receiver sensitivity [ Pa/V ] V is the voltage o/p measured at receiver 0 RS RL SL TL TS this is the voltage measured at the receiver – more commonly this would be in counts, which is then converted to volts 14 Oc 679 Acoustical Oceanography

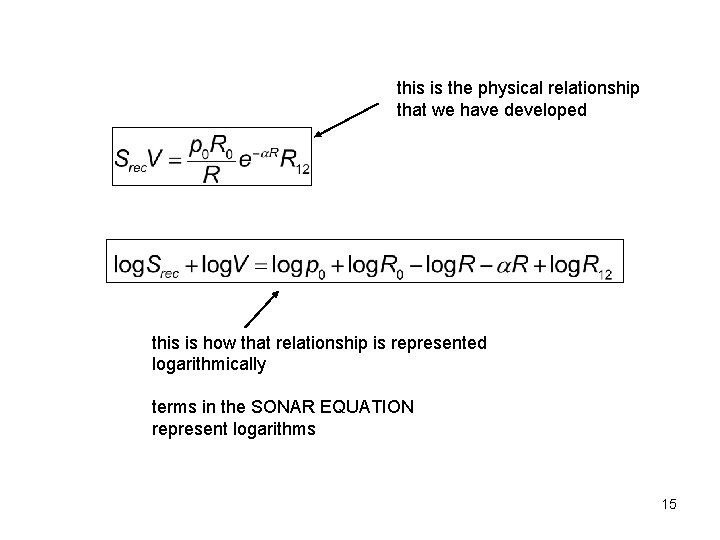
this is the physical relationship that we have developed this is how that relationship is represented logarithmically terms in the SONAR EQUATION represent logarithms 15

let’s take a step back now that we have seen how the SONAR EQUATION is formed the physics is straightforward as is the transformation to a logarithmic equations – more straightforward than is implied by the large number of variations to the SONAR EQUATION that appear – these are usually specific to the application and intended for unambiguous use by operators we’ll look at a couple of variations 16

Passive SONAR EQUATION passive sonars listen only purpose – detection, classification and localization of an acoustic source in turn, a particular source is embedded in a sea of sources suppose a radiating object of source level SL (decibels) is received at a hydrophone at a lower signal level S due to transmission loss TL (TL always > 0) S = SL – TL this is the logarithmic representation of where we have already defined TL = 20 log 10 R + 20 R to be due to the product of absorption and spreading (which appear additively in this logarithmic representation) and we could represent the signal to noise ratio at the hydrophone as SNR = SL – TL – N logarithmic representation of 17

DI directivity index SNR can be increased by beam-forming so that sound does not spread spherically but is more directional for an omnidirectional source I is proportional to 4πR 2 here it is constrained to πr 2 where r might be the piston diameter of a cylindrical source Define DI = 10 log(intensity of acoustic beam /intensity of omnidirectional source) r S R=1 m r α/2 DI = 10 log ((p/πr 2)/(p/4πR 2)) with R = 1 DI = 10 log (4/r 2) and tan(α) = r/R = r DI = 10 log (4/tan 2(α/2)) 18

SNR can be increased by beam-forming produced by an array of transducers (perhaps in a single head or maybe distributed geographically) the directivity index DI represents this advantage for a particular array so that SNR = SL – TL – N + DI ideally, detection is possible when the signal is sufficiently close and not disguised by noise … that is, when SNR > 0 however, due to the nature of the signal, interference, the sonar operator’s training and alertness, etc … something more than 0 is necessary this extra appears as a detection threshold, DT we now write the SONAR EQUATION in terms of a signal excess SE SE = SL – TL – N + DI – DT this is now the difference between the actual received signal at the output of the beamformed array and minimum signal required for detection 19

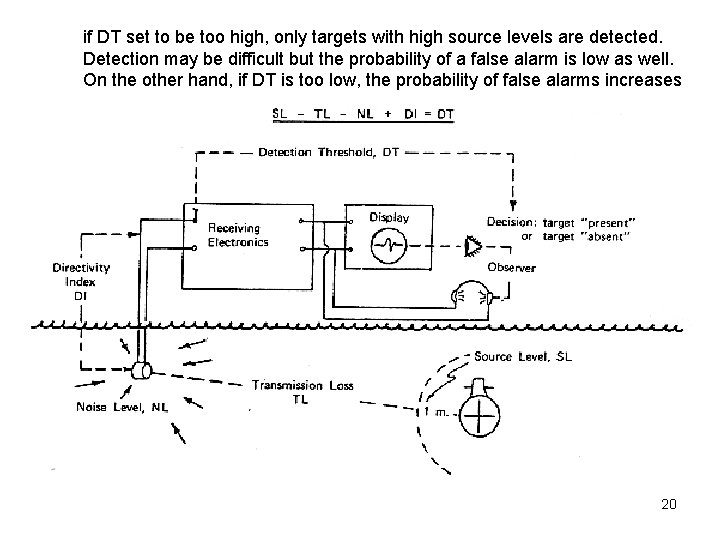
if DT set to be too high, only targets with high source levels are detected. Detection may be difficult but the probability of a false alarm is low as well. On the other hand, if DT is too low, the probability of false alarms increases 20

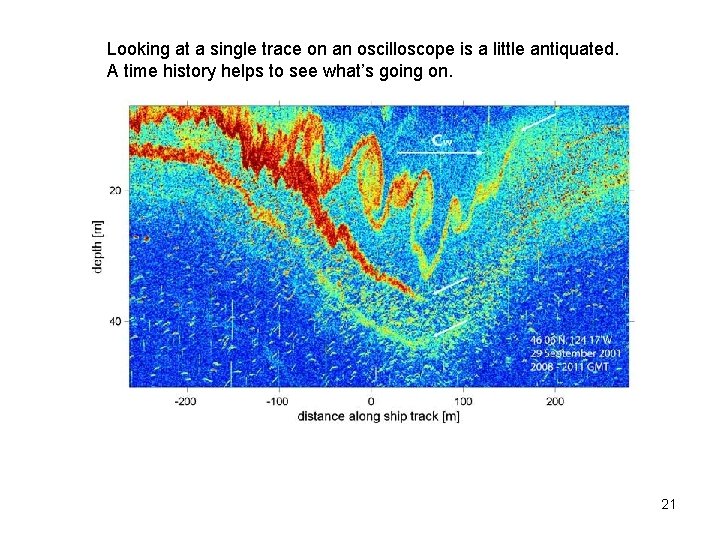
Looking at a single trace on an oscilloscope is a little antiquated. A time history helps to see what’s going on. 21

Active SONAR EQUATION now the transducer transmits a signal that is reflected or scattered from an object – the modified signal is sensed at the receiver (which may be the same as the source, in monostatic mode) this modified signal must be extracted from the background interference which is not only the sonar noise and ambient noise, but also the reverberation generated by the original signal simple example – travel-time measurement of the echo to estimate the distance to an object (such as a fathometer which measures water depth by listening to the echo of a ping off the sea floor) we can simply say that the sound pressure level SPL at range R is SPL = SL - TL 22

three principal differences from passive case 1. received signal level modified by target strength TS 2. reverberation is the dominant interference 3. transmission loss results from 2 paths transmitter to target + target to receiver monostatic - transmission loss is 2 TL bistatic - transmission loss is TL 1 + TL 2 Reverberation Level RL results primarily from scattering of the transmitted signal from things other than the target of interest boundary scattering may be due to waves, ice bottom features volume scattering may be due to zooplankton, fish, microstructure, … this means that the total interference term is due to the sum of the noise and the reverberation N + RL – these act to diminish our ability to detect TS 23

Homework 1 – Martin Hoecker-Martinez 18 Jan 2011 http: //wart. coas. oregonstate. edu/Documents/for%20 others/jim/150 W. gif 24

So, there are essentially two types of background that may mask the signal that we wish to detect: 1) Noise background or Noise Level (NL). This is an essentially a steady state, isotropic (equal in all directions) sound which is generated by amongst other things wind, waves, biological activity and shipping. This is in addition to transducer system self-noise. (Wenz curves) 2) Reverberation background or reverberation level (RL). This is the slowly decaying portion of the back-scattered sound from one's own acoustic input. Excellent reflectors in the form of the sea surface and floor bound the ocean. Additionally, sound may be scattered by particulate matter (e. g. plankton) within the water column. You will have experienced reverberation for yourself. For example if you shout loudly in a cave you are likely to here a series of echoes reverberating due to sound reflections from the hard rock surfaces. These reverberations decay rapidly with time. Although both types of background are generally present simultaneously it is common for either one or the other to be dominant. 25

we could define SONAR EQUATION for a monostatic system as SE = SL – 2 TL + TS – (RL + N) + DI – DT And for a bistatic system SE = SL – TL 1 + TS – TL 2 – (RL + N) + DI – DT 26

Sound scattered by a body - RL in SONAR EQUATION scattering is the consequence of the combined processes of reflection, refraction and diffraction at surfaces marked by inhomogeneities in c - these may be external or internal to a scattering volume ( internal inhomogeneities important when considering scattering from fish, for example ) net result of scattering is a redistribution of sound pressure in space – changes in both direction and amplitude the sum total of scattering contributions from all scatterers is termed reverberation this is heard as a long, slowly decaying quivering tonal blast following the ping of an active sonar system consideration usually begins by considering scattering from spheres 27 Oc 679 Acoustical Oceanography

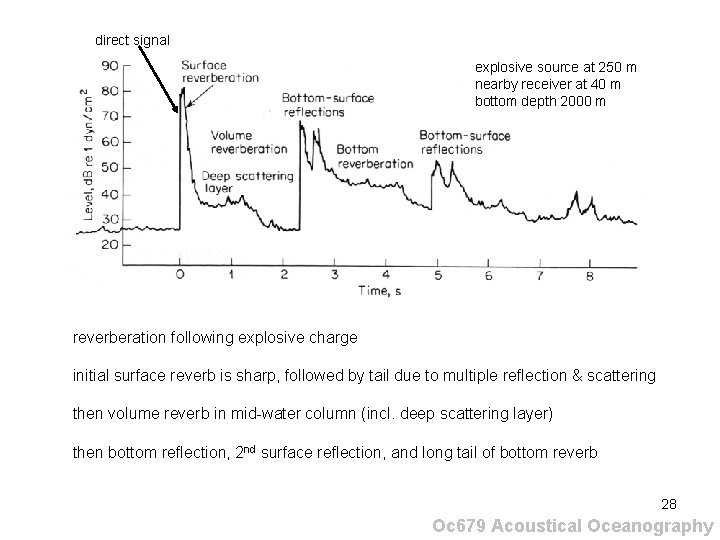
direct signal explosive source at 250 m nearby receiver at 40 m bottom depth 2000 m reverberation following explosive charge initial surface reverb is sharp, followed by tail due to multiple reflection & scattering then volume reverb in mid-water column (incl. deep scattering layer) then bottom reflection, 2 nd surface reflection, and long tail of bottom reverb 28 Oc 679 Acoustical Oceanography

sounds in the sea or N in the SONAR EQUATION natural physical sounds natural biological sounds ships 29 Oc 679 Acoustical Oceanography

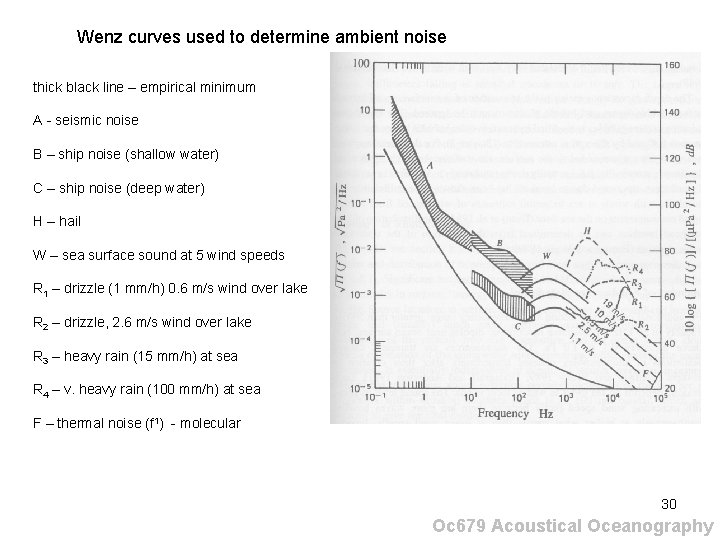
Wenz curves used to determine ambient noise thick black line – empirical minimum A - seismic noise B – ship noise (shallow water) C – ship noise (deep water) H – hail W – sea surface sound at 5 wind speeds R 1 – drizzle (1 mm/h) 0. 6 m/s wind over lake R 2 – drizzle, 2. 6 m/s wind over lake R 3 – heavy rain (15 mm/h) at sea R 4 – v. heavy rain (100 mm/h) at sea F – thermal noise (f 1) - molecular 30 Oc 679 Acoustical Oceanography

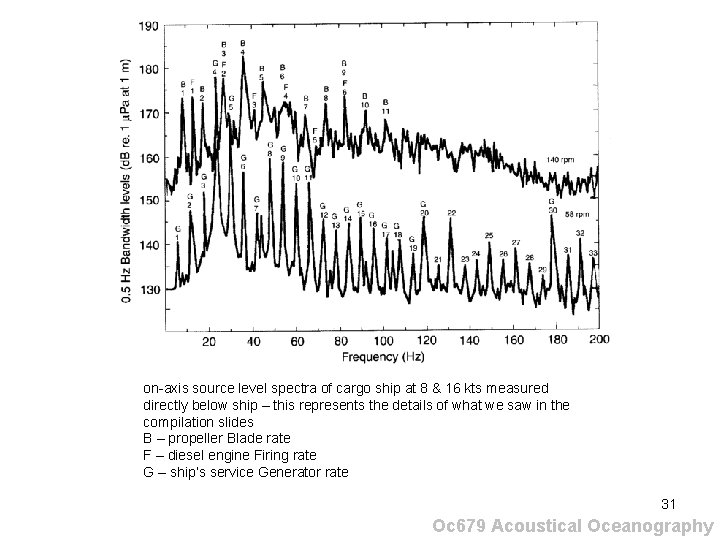
on-axis source level spectra of cargo ship at 8 & 16 kts measured directly below ship – this represents the details of what we saw in the compilation slides B – propeller Blade rate F – diesel engine Firing rate G – ship’s service Generator rate 31 Oc 679 Acoustical Oceanography

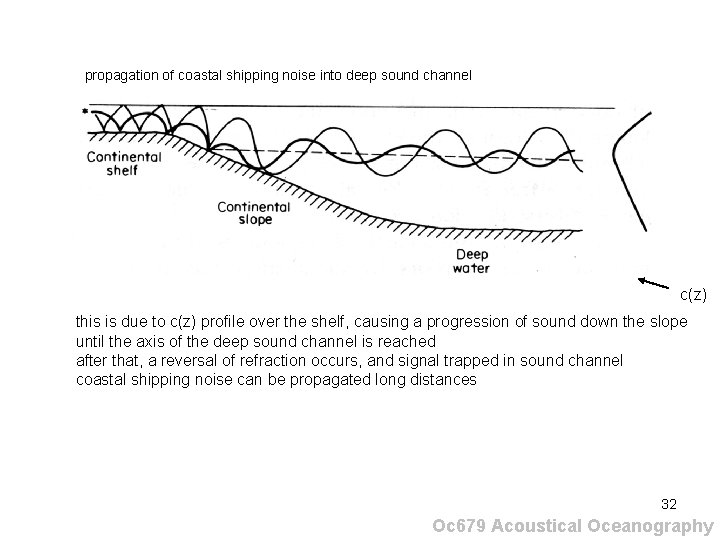
propagation of coastal shipping noise into deep sound channel c(z) this is due to c(z) profile over the shelf, causing a progression of sound down the slope until the axis of the deep sound channel is reached after that, a reversal of refraction occurs, and signal trapped in sound channel coastal shipping noise can be propagated long distances 32 Oc 679 Acoustical Oceanography

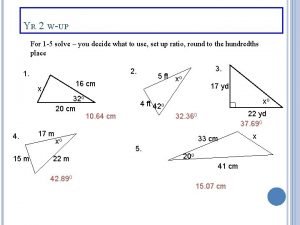
Homework Assignment 2 assigned: due: 18 Jan 2010 27 Jan 2010 A yellow submarine is conducting a passive search against blue submarines. Yellow submarines have a sonar with directivity index of 15 d. B and detection threshold 8 d. B. Blue submarines have known source level 140 d. B. Environmental conditions yield an isotropic noise level of 65 d. B. You can assume an absorption decay coefficient 0. 02 d. B/km. At what range can the blue submarine be detected by the yellow submarine? Show your answer graphically. 33

34

35 Oc 679 Acoustical Oceanography