Solving Quadratic Equations What does x Solving Quadratic





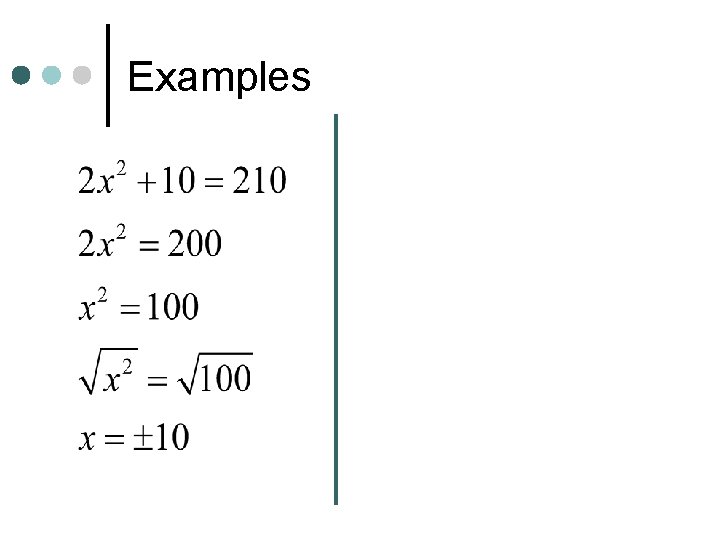
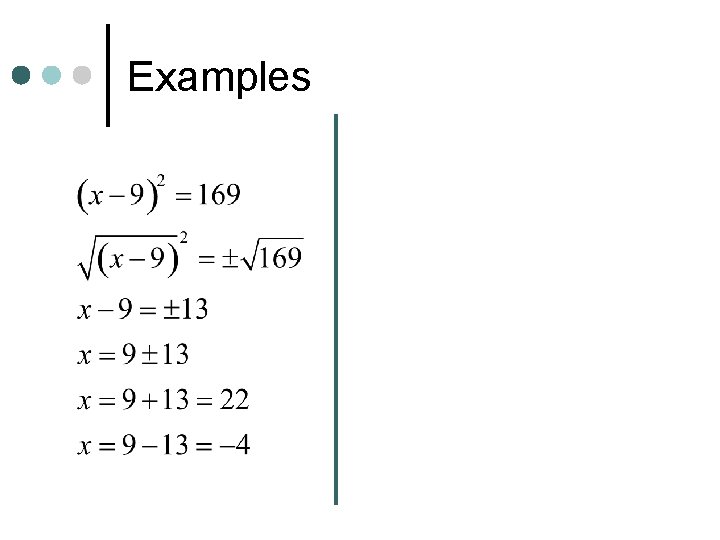



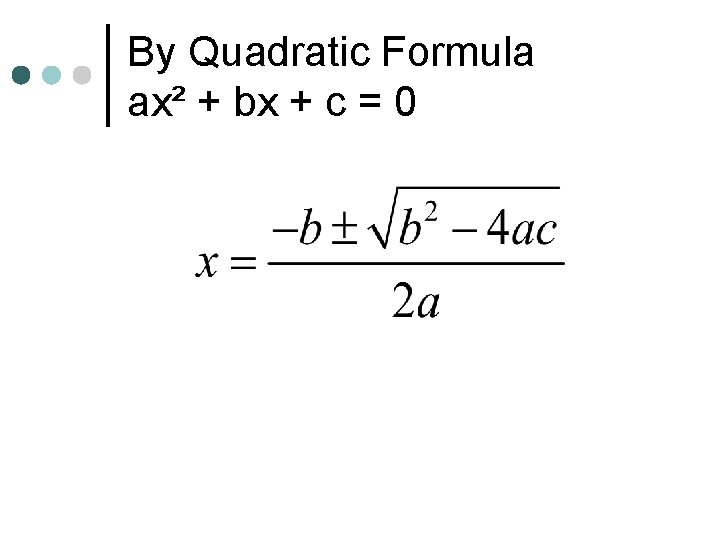




- Slides: 15

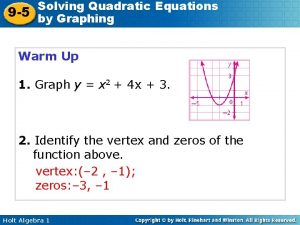
Solving Quadratic Equations What does x = ? ? ?

Solving Quadratic Equations What does x =? ¢ Five different ways: l l l ¢ By Graphing By Factoring By Square Root Method By Completing the Square By Quadratic Formula Number of Solutions: l There can be either 1 or 2 solutions to a quadratic equation.

Classification of Solutions ¢ Solutions to quadratic equations are called: “Roots” of the equation l “Zeros” of the function l ¢ Solutions can be: Real (Rational or Irrational) l Complex (Imaginary) l

Classifying Solutions must be in simplified radical form ¢ If no radicals left, answers are rational. ¢ If radical left, answers are irrational. ¢ Watch out! ¢ l If taking the square root of a negative number, answers are complex (imaginary)!!!!

By Taking Square Root ¢ First you must isolate the x² or (x-h)² term. ¢ Then, take the square root of both sides. ¢ You will use ± (plus/minus) for the answer.
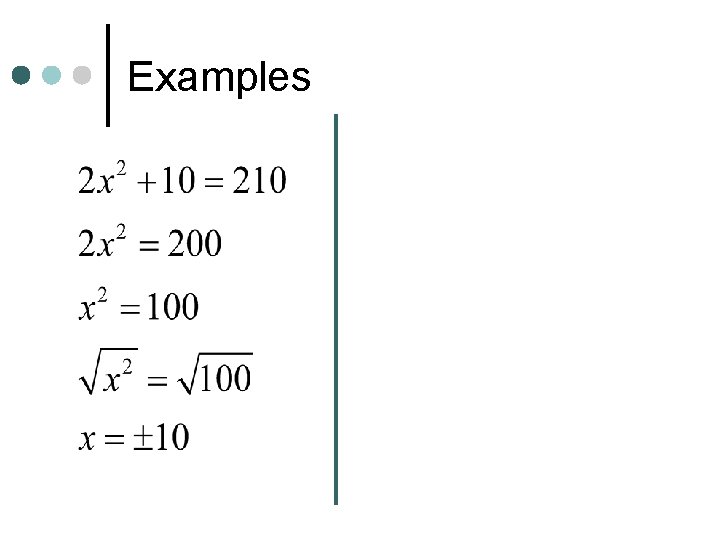
Examples
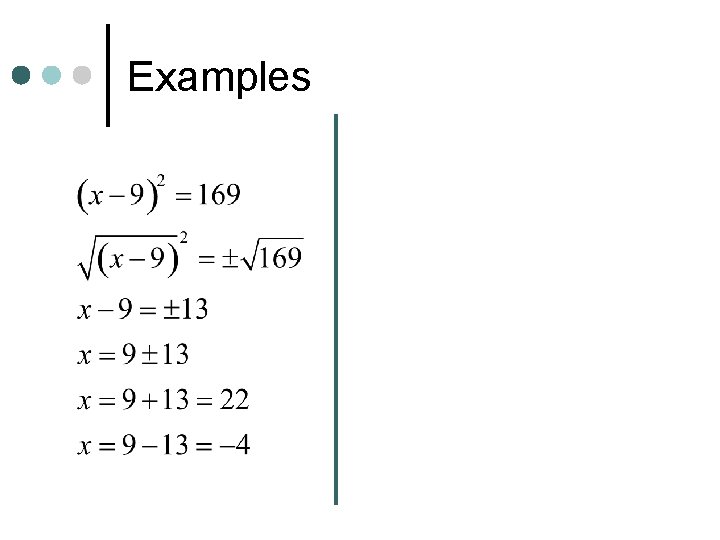
Examples

By Factoring ¢ Place equation in standard form: ax² + bx + c = 0 ¢ Factor the expression ¢ Use the Principle of Zero Product Rule to solve for x. ¢ To classify: l If the expression is factorable, the solutions are “rational” • (There will be either 1 or 2 solutions) l If the expression is prime (not factorable), the solutions may be irrational or complex – not enough info to decide!

Solve Quadratic equation by factoring example ¢ ¢ ¢ Example: Put in standard form first: Factor Use principle of zero product rule (if multiplying two things together and =0, then one of those things must be 0. ) The GCF of 4 has no relevance to final answer.

By Completing the Square ¢ Complete the square, then isolate the (x-h)² term. ¢ Solve by square root method.
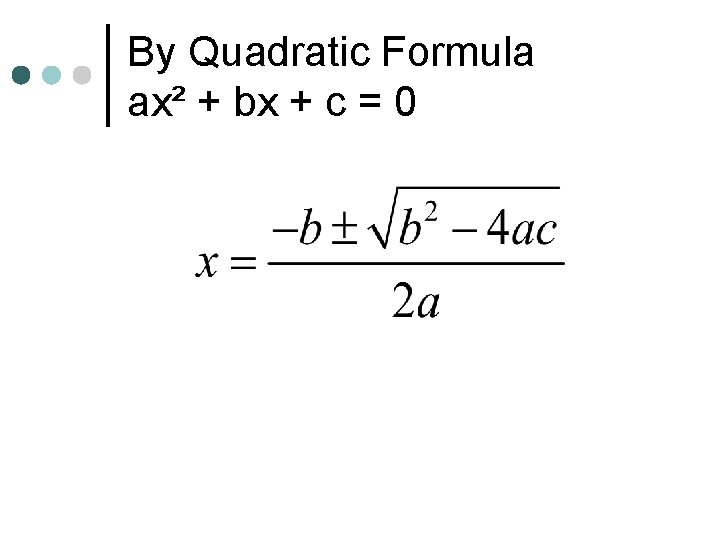
By Quadratic Formula ax² + bx + c = 0

By Graphing ¢ You have done this! Graph one side of equation in Y 1, other side in Y 2. ¢ 2 nd Calc Intersect to find the intersection of the two functions. ¢ Classify solutions: l If graphs intersect twice, there are 2 solutions. (2 real solutions) ¢ l If graphs intersect once, there is 1 solution (1 real solution) l If graphs never intersect, there are no “real” solutions, but there are 2 complex solutions

Discriminant-used to classify solutions of quadratic equations ¢ The discriminant is the radicand portion of the quadratic formula: Discriminant = b²-4 ac If discriminant = 0, one rational solution If discriminant = perfect square number, 2 rational solutions If discriminant = non-perfect square number, 2 irrational solutions If discriminant = negative number, 2 complex solutions

Solving Word Problems that are quadratic (area problems) ¢ ¢ ¢ Draw a picture! Find an expression for length and width in terms of a variable. Find an expression for area in terms of the variable. Set the actual number for area equal to the expression. Put quadratic equation in standard form (set = 0) Factor and solve by factoring.

Word Problem Example ¢ A square garden is increased by 2 on one side and decreased by 3 on the other, to form a rectangular garden. The area of the new garden is 50 m². Find the dimensions of the original garden. v. The dimensions of the new rectangle are (x + 2) by (x-3) v. Area of the new rectangle is (x + 2)(x – 3) or x² - x -6. xm 3 xm v. The dimensions of the original square x by x m. x-3 x+2 The original dimensions of the square is 8 x 8. The new dimensions are 10 x 5
 Essential questions for quadratic functions
Essential questions for quadratic functions Solving quadratic equations algebraically
Solving quadratic equations algebraically How do i solve a quadratic equation
How do i solve a quadratic equation Solving quadratic equations by square root property
Solving quadratic equations by square root property Zero product property.
Zero product property. One solution quadratic equation
One solution quadratic equation 5-3 solving quadratic equations by factoring
5-3 solving quadratic equations by factoring 9-7 solving quadratic equations by using square roots
9-7 solving quadratic equations by using square roots Lesson 9-6 solving quadratic equations by factoring answers
Lesson 9-6 solving quadratic equations by factoring answers 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing Solve quadratic equation
Solve quadratic equation Solving quadratic equations by factoring gcf worksheet
Solving quadratic equations by factoring gcf worksheet Graphing quadratic functions vocabulary
Graphing quadratic functions vocabulary How to solve quadratic equations by elimination
How to solve quadratic equations by elimination