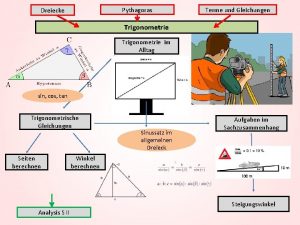
Sistemas de Equaes Lineares 20 aula Em que














- Slides: 19

Sistemas de Equações Lineares 20ª aula

Em que situações devemos resolver um sistema de equações Resolver sistemas de equações é necessário em qualquer estudo onde se pesquise a interação de variáveis em determinado fenômeno ou experimento.

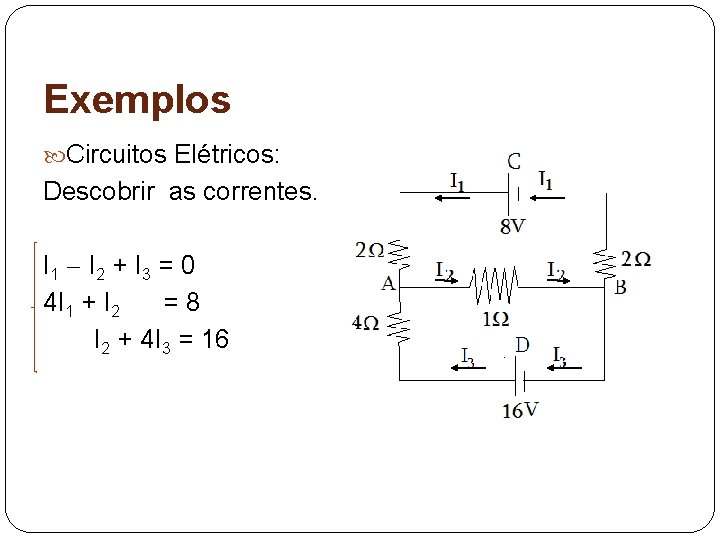
Exemplos Circuitos Elétricos: Descobrir as correntes. I 1 I 2 + I 3 = 0 4 I 1 + I 2 =8 I 2 + 4 I 3 = 16

Exemplos Balanceamento de equações químicas w. NH 3 + x O 2 y. N 2 + z. H 2 O w = 2 y 3 w = 2 z 2 x = z

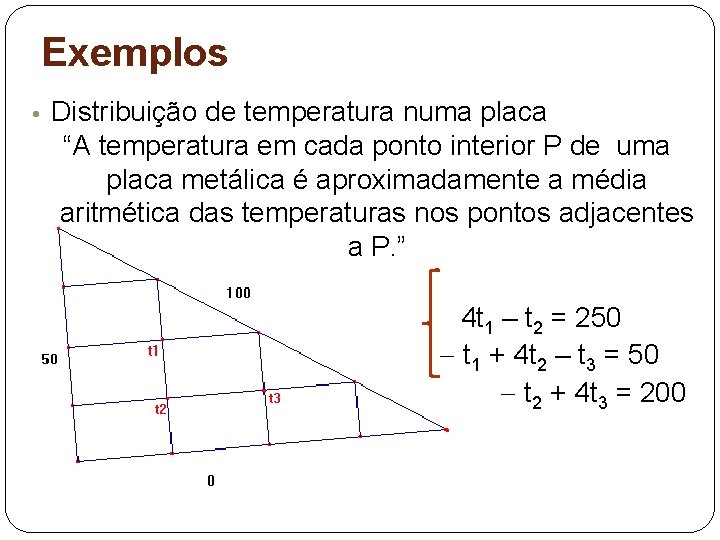
Exemplos • Distribuição de temperatura numa placa “A temperatura em cada ponto interior P de uma placa metálica é aproximadamente a média aritmética das temperaturas nos pontos adjacentes a P. ” 4 t 1 – t 2 = 250 t 1 + 4 t 2 – t 3 = 50 t 2 + 4 t 3 = 200

O que é uma equação linear? Equação com certo número de variáveis onde cada termo não pode ter grau diferente de 1. Exemplo: 3 x + y – 6 z + w = 3 xy + 5 z = 7 Produto de duas variáveis de grau 1 tem grau 2. Equivale x-1, o grau não é 1

Sistemas de Equações Lineares • Conjunto de equações lineares. Exemplos: x+y–z=7 2 x – 4 y + z = 0 x+y=3 13 3 equações 3 incógnitas x + y – 3 z + w = 0 x – y + z + 2 w = 5 2 x – y – z – w = 3 x – 2 y + z = 8 3 x + y – z = 1 x+y+z=2 x – y – 3 z = 3 equações 4 4 incógnitas 3

Solução de Um sistema A maioria PENSA que SABE e que é FÁCIL resolver um sistema de equações lineares. Resolva o seguinte sistema o mais rápido que puder: x + 2 y + 3 z = 1 2 x + y + z = 2 3 x y + 2 z = 1 S=

Tipos de solução Uma solução. Exemplo: x+y–z=7 2 x – 4 y + z = 0 x+y=3 S={ }, ou seja, x = 8/3, y = 1/3 e z = 4.

Tipos de solução Infinitas soluções: Exemplo: x + y – 3 z + w = 0 x – y + z + 2 w = 5 2 x – y – z – w = 3 Possui infinitas soluções, pois neste caso o sistema possui mais incógnitas do que equações. Algumas quádruplas que verificam o sistema: (13, 15, 9, -1) e (1, -2, 0, 1).

Tipos de solução Nenhuma solução Exemplo: x+y–z=7 2 x – 4 y + z = 0 x+y–z=3 Absurdo! Não existe trio x, y e z que satisfaça essas equações ao mesmo tempo.

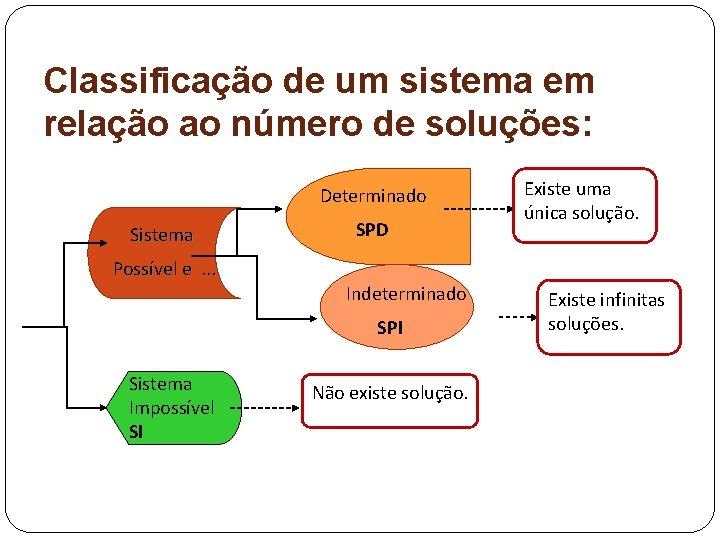
Classificação de um sistema em relação ao número de soluções: Determinado Sistema Possível e. . . SPD Indeterminado SPI Sistema Impossível SI Não existe solução. Existe uma única solução. Existe infinitas soluções.

Sistemas de duas equações e duas incógnitas e sua interpretação geométrica Sistemas 2 x 2 são fáceis de resolver, seja qual for o método. Exemplo: Resolva, em l. R: 2 x+ y = 3 x – 2 y = 4 S={(2, 1)}

Interpretação Geométrica Cada equação linear de duas variáveis é a equação de uma reta: y = 2 x + 3 (forma da função afim) coef. angular a = 2 coef. linear : b = 3 2 x+y=3 x – 2 y = 4 coef. angular coef. linear: b = 2

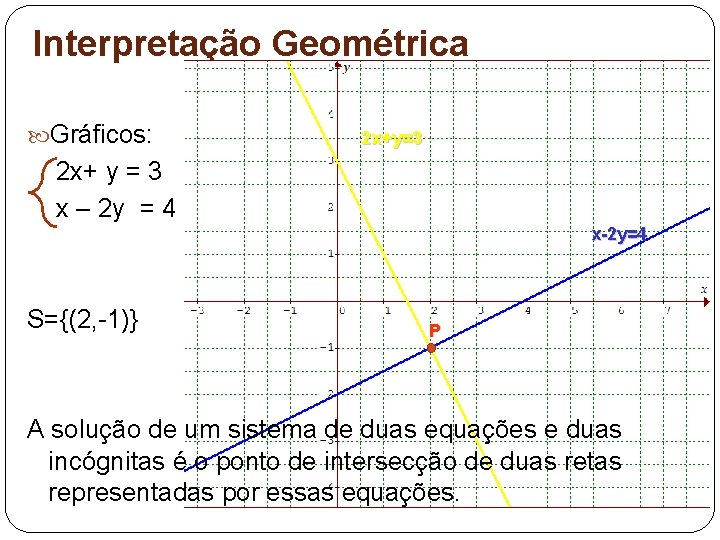
Interpretação Geométrica Gráficos: 2 x+y=3 2 x+ y = 3 x – 2 y = 4 x-2 y=4 S={(2, -1)} P A solução de um sistema de duas equações e duas incógnitas é o ponto de intersecção de duas retas representadas por essas equações.

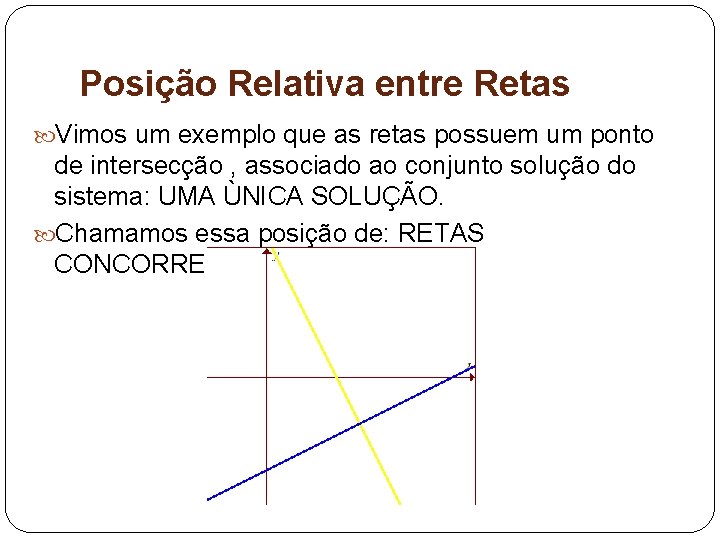
Posição Relativa entre Retas Vimos um exemplo que as retas possuem um ponto de intersecção , associado ao conjunto solução do sistema: UMA ÙNICA SOLUÇÃO. Chamamos essa posição de: RETAS CONCORRENTES.

Posição Relativa entre Retas Exemplo: 6 x – 3 y = 1 2 x – y = 3 6 x-3 y=1 Sistema Impossível. Como são as retas associadas às equações? 2 x-y=3 Não possuindo intersecção , as retas são: PARALELAS.

Posição Relativa entre Retas Exemplo: 2 x + 2 y = 8 x+y=4 Infinitas soluções. São duas maneiras diferentes de apresentar a mesma equação. 2 x+2 y=8 x+y=4 Nessa situação dizemos que as retas são COINCIDENTES.

Exercícios Resolva os sistemas abaixo e determine a posição relativa entre as retas relacionadas: (a) r: 3 x + 4 y = - 7 e s: x + y = -1 (b) t: 5 x – 10 y = 7 e r: x – 2 y = 6 (c) v: 2 x + 4 y = 14 e u: x + 2 y = 7 (d) s: 2 x – 3 y = 11 e v : 6 x – 4 y = 3.
 Análise de sistemas lineares
Análise de sistemas lineares Regra de cramer
Regra de cramer Sistemas lineares escalonamento
Sistemas lineares escalonamento Equaes
Equaes Resolver equações em ordem a x
Resolver equações em ordem a x Desembaraçar de parênteses
Desembaraçar de parênteses Equação diferencial
Equação diferencial Autovalores
Autovalores Lineares gleichungssystem
Lineares gleichungssystem Listas lineares
Listas lineares Difmos
Difmos Regelungen
Regelungen Lineare funktionen alltag
Lineare funktionen alltag O que significa
O que significa De acordo com que vimos durante a aula
De acordo com que vimos durante a aula Uma sala de aula possui 100 alunos sendo que 40
Uma sala de aula possui 100 alunos sendo que 40 Enfoque clasico expansionismo
Enfoque clasico expansionismo Monotareas sistemas operativos
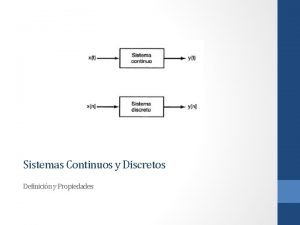
Monotareas sistemas operativos Sistemas continuos
Sistemas continuos Funcion del sistema respiratorio
Funcion del sistema respiratorio