3 Equaes Lineares de Segunda Ordem Equaes homogneas

![Assim, a equação [1] pode ser escrita como y ” + p(t)y’ + q(t)y Assim, a equação [1] pode ser escrita como y ” + p(t)y’ + q(t)y](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-2.jpg)

![A equação [2] pode ser escrita na forma algébrica ar 2 + br + A equação [2] pode ser escrita na forma algébrica ar 2 + br +](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-4.jpg)



![Soluções fundamentais de equações lineares homogêneas Definimos o operador diferencial L por L[ ] Soluções fundamentais de equações lineares homogêneas Definimos o operador diferencial L por L[ ]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-8.jpg)

![Teorema: Se y 1 e y 2 são soluções da equação diferencial L[y] = Teorema: Se y 1 e y 2 são soluções da equação diferencial L[y] =](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-10.jpg)
![Teorema. Se y 1 e y 2 são duas soluções da equação diferencial L[y] Teorema. Se y 1 e y 2 são duas soluções da equação diferencial L[y]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-11.jpg)






![Equações não homogêneas; método dos coeficientes a determinar Dada a equação não homogênea L[y] Equações não homogêneas; método dos coeficientes a determinar Dada a equação não homogênea L[y]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-18.jpg)










![Equação homogênea com coeficientes constantes Seja a equação L[y] = a 0 yn +a Equação homogênea com coeficientes constantes Seja a equação L[y] = a 0 yn +a](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-29.jpg)



- Slides: 32

3 - Equações Lineares de Segunda Ordem Equações homogêneas com coeficientes constantes. Uma equação diferencial de segunda ordem tem a forma (d 2/dt 2) = f (t, y, dy/dt) [1] onde f é alguma função dada. A equação [1] é dita linear se a função f tem a forma f(t, y, dy/dt) = g(t) – p(t)dy/dt – q(t)y Isto é, se f é linear em y e y’. Deve-se notar que g, p e q são funções da variável independente t, não dependem de y.
![Assim a equação 1 pode ser escrita como y pty qty Assim, a equação [1] pode ser escrita como y ” + p(t)y’ + q(t)y](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-2.jpg)
Assim, a equação [1] pode ser escrita como y ” + p(t)y’ + q(t)y = g(t) ou comumente escrita como P(t)y ” + Q(t)y’ + R(t)y = G(t), p(t) = Q(t) / P(t), q(t) = R(t) / P(t) Se e P(t) 0, g(t) = G(t) / P(t) Um problema de valor inicial consiste em uma equação diferencial, como antes, junto com um par de condições iniciais y(t 0) = y 0 e y’(t 0) = y 0’ onde y 0’ são números dados. Uma equação linear de segunda ordem é dita homegênea se a função g(t) ou G(t) for igual a zero para todo t.

Assim, P(t)y” + Q(t)y’ + R(t)y = 0. Vamos considerar P, Q e R constantes. E assim, temos ay” + by’ + cy = 0 [2] onde a, b e c são constantes dadas. Exemplo 1: Resolva a equação y” – y = 0. Temos neste caso a = 1, b = 0 e c = - 1. Isto significa procurar uma função cuja derivada segunda é igual a ela mesma. Facilmente identificamos que y 1(t) = e t e y 2 (t) = e -t c 1 y 1 (t) = c 1 e t e servem. Também servem c 2 y 2 (t) = c 2 e -t E mais y = c 1 y 1 (t) + c 2 y 2 (t) = c 1 e t + c 2 e -t , para c 1 e c 2 quaisquer.
![A equação 2 pode ser escrita na forma algébrica ar 2 br A equação [2] pode ser escrita na forma algébrica ar 2 + br +](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-4.jpg)
A equação [2] pode ser escrita na forma algébrica ar 2 + br + c = 0 [3] fazendo y” = r 2, y’ = r e y =1 = r 0 respectivamente. Esta equação é chamada de equação característica. O fato é que se r é raiz da equação polinomial [3], então y = e rt é solução da equação diferencial [2]. Supondo que r 1 e r 2 são raizes distintas de [3], então y 1(t) = e r t e y 2(t) = e r t são duas soluções da equação diferencial ou como no exemplo anterior, 1 2 y = c 1 y 1(t) + c 2 y 2(t) = c 1 e r t + c 2 e r t 1 2 que também é solução da equação dada.

Exemplo 2: Encontre a solução da equação y” – y’ – 2 y = 0. Nesta caso, a equação característica é r 2 – r – 2 = 0, (r+1)(r-2) = 0, r 1 = - 1 e r 2 = 2. Logo, y = c 1 e – t + c 2 e 2 t Exemplo 3: Resolva a equação diferencial y” + 5 y’ + 6 y = 0, com y(0) = 2 e y’(0) = 3. A equação característica é r 2 + 5 r + 6 = 0, (r + 2)(r + 3) = 0. Logo y = c 1 e - 2 t + c 2 e - 3 t. Pela primeira condição, temos y(0) = 2 = c 1 + c 2 Pela segunda condição, y’(0) = - 2 c 1 e – 2 x 0 – 3 c 2 e - 3 x 0 = 3 = -2 c 1 – 3 c 2

Logo c 1 + c 2 = 2 -2 c 1 – 3 c 2 = 3 Donde c 2 = - 7 e c 1 = 9. Assim y = 9 e – 2 t - 7 e – 3 t Para uma equação de segunda ordem, sem a variável independente, da forma y” = f(t, y”), a substituição v = y’ e v’ = y” leva a uma equação de primeira ordem da forma v’ = f(t, v). Se ela puder ser resolvida em v, então y pode ser encontrada integrando-se dy / dt = v. Exemplo 4: Resolva a equação y” + y’ = e – t. Fazendo v’ = y”, v = y’, temos v’ + v = e – t.

Tomando a função integrante (t) = e t, temos e t v’ + v e t = e -t e t ou ( e t v )’ = 1 e t v = t + c 1 v = te -t + c 1 e -t Ora, como dy/dt = v = te -t + c 1 e -t , temos, por partes te -t dt, u = t, du = dt, dv = e -t dt, v = - e –t, Logo, y = te -t dt + c 1 e -t dt = - te -t - -e -t dt – c 1 e -t = - c 1 e -t + c 2 – te -t – e –t y = c 1 e -t + c 2 – te -t
![Soluções fundamentais de equações lineares homogêneas Definimos o operador diferencial L por L Soluções fundamentais de equações lineares homogêneas Definimos o operador diferencial L por L[ ]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-8.jpg)
Soluções fundamentais de equações lineares homogêneas Definimos o operador diferencial L por L[ ] = ’’ + p ’ + q onde p e q são funções contínuas em I. O valor de L[ ] em t é dado por L[ ](t) = ’’(t) + p(t) ’(t) + q(t) (t). O operador L é normalmente usado como L = D 2 + p. D + q, onde D é o operador derivada. Usando y para representar (t), temos L[y] = y’’ + p(t) y’(t) + q(t) y = 0 e as condições y (t 0) = y 0 e y’ (t 0) = y 0’.

Teorema: Considere o problema de valor inicial y’’ + p(t) y’(t) + q(t) y = g(t), y (t 0) = y 0, y’ (t 0) = y 0’ onde p , q e g são funções contínuas em um intervalo aberto I. Então, existe exatamente uma solução y = (t) desse problema e a solução existe em todo intervalo I. Exemplo: Encontre o maior intervalo no qual a solução do problema (t 2 – 3 t) y’’ + t y’ – (t +3) y = 0, y (1) = 2, y’ (1) = 1, certamente existe. Solução: Calculando a forma do teorema acima, temos p(t) = 1 / (t-3), q(t) = - (t+3) / ( t 2 – 3 t) e g(t) = 0. Os pontos de descontinuidade são t = 0 e t = 3. Logo o maior intervalo contendo a condição inicial t =1 é 0 < t < 3.
![Teorema Se y 1 e y 2 são soluções da equação diferencial Ly Teorema: Se y 1 e y 2 são soluções da equação diferencial L[y] =](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-10.jpg)
Teorema: Se y 1 e y 2 são soluções da equação diferencial L[y] = y’’ + p(t) y’ + q(t) y = 0, então a combinação linear c 1 y 1 + c 2 y 2 também é solução , quaisquer que sejam os valores das constantes c 1 e c 2. Teorema: Suponha que y 1 e y 2 são duas soluções de L[y] = y’’ + p(t) y’ + q(t) y = 0 e que o wronskiano w = y 1 y 2’ - y 1’y 2 não se anule no ponto t 0, onde são dadas as condições iniciais y (t 0) = y 0, y’ (t 0) = y 0’. Então, existe uma escolha das constantes c 1 e c 2 para os quais y = c 1 y 1(t) + c 2 y 2(t) satisfaz a equação diferencial acima e as condições iniciais y (t 0) = y 0, y’ (t 0) = y 0’.
![Teorema Se y 1 e y 2 são duas soluções da equação diferencial Ly Teorema. Se y 1 e y 2 são duas soluções da equação diferencial L[y]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-11.jpg)
Teorema. Se y 1 e y 2 são duas soluções da equação diferencial L[y] = y’’ + p(t) y’ + q(t) y = 0, e existe um ponto onde o wronskiano de y 1 e y 2 é diferente de zero, então a família de soluções y = c 1 y 1(t) + c 2 y 2(t) com coeficientes arbitrários c 1 e c 2 , inclui todas as soluções da equação acima. Teorema. Considere a equação diferencial L[y] = y’’ + p(t) y’ + q(t) y = 0, cujos coeficientes p e q são contínuos em algum intervalo aberto I. Escolha algum ponto t 0 em I. Seja y 1 a solução da equação acima que satisfaz, também, as condições iniciais y(t 0) = 1 e y´(t 0) = 0, e seja y 2 a solução da equação acima que satisfaz as condições iniciais y(t 0) = 0 e y´(t 0) = 1. Então, y 1 e y 2 formam um conjunto fundamental de soluções.

Exemplo: Determine o valor do Wronskiano do par de funções y 1 = e 2 t e y 2 = e – 3 t/2. Solucão: Como w = y 1 y 2` - y 1` y 2 temos e 2 t (- 3/2 e – 3 t/2) - 2 e 2 t e – 3 t/2 = -7/2 e t/2 Raízes complexas de equações características Já vimos que a solução da equação ay’’ + by’ + cy = 0, com a, b e c reais, temos a equação característica ar 2 +br + c = 0 e se r 1 e r 2 são raizes, então y = c 1 e r 1 t + c 2 e r 2 t. Porém, se as raízes forem complexas denotamos por r 1 = + i e r 2 = - i onde e são reais. As representações para y 1 e y 2 são y 1 (t) = exp[( + i )t] e y 2 = exp[( - i )t]

Fórmulas de Euler Do cálculo elementar, usando a série de Taylor, temos para e t em torno de t = 0, Nos complexos, temos Onde foram separadas as partes real e imaginária observando os valores das potencias i 2 = -1, i 3 = -i, i 4 = 1, etc. Note que a primeira parte desta série é a série de Taylor para cos(t) em torno de t = 0 e a segunda é a série de Taylor para sen(t) em torno de t = 0.

Logo e it = cost + i sent ou e -it = cost - i sent ou a fórmula generalizada de Euler e i t = cos( t) + i sen( t). Solução: y = c 1 e t cos( t) + c 2 e t sen( t), onde ± i são raízes da equação característica. Exemplo: Encontre a solução geral da equação diferencial y” + y = 0. Solução: A equação característica é dada por r 2 + 1 = 0. Logo r = i. Então y = c 1 cost + c 2 sent, pois temos = 0 e = 1.

Exemplo: Encontre a solução do problema de valor inicial dado por y” + 4 y = 0, y(0) = 0 e y`(0) = 1. Solução: Temos a equação característica r 2 + 4 = 0 que nos leva a r = 2 i. Logo y = c 1 cos(2 t) + c 2 sen(2 t). Então y(0) = c 11 + c 20 = 0 c 1 = 0. Como y’ = - 2 c 1 sen(2 t) + 2 c 2 cos(2 t), temos y’(0) = 0 + 2 c 2 = 1 Logo a solução é c 2 = 1/2. y = 0 + ½ sen(2 t) = ½ sen(2 t)

Raízes repetidas Se as raízes forem repetidas r 1 = r 2 = - b/2 a, então y 1 = e –bt / 2 a e y 2 = te –bt / 2 a logo, se r 1 = r 2 A solução geral é y = c 1 e r 1 t + c 2 te r 1 t Exemplo: Encontre a solução geral da equação ordinária y’’ – 2 y’ + y = 0. Solução: Temos a equação característica r 2 - 2 r +1 = 0 e consequentemente r = 1. Logo a solução é dada por y = c 1 e t + c 2 te t

Exemplo: Determine a solução da equação diferencial y” – 6 y’ + 9 y = 0, y(0) = 0, y’(0) = 2. Solução: Temos a equação característica r 2 - 6 r + 9 = 0, cujo solução é dada por r 1 = r 2 = 3. Assim, y = c 1 e 3 t + c 2 te 3 t Logo, y(0) = c 1 + 0 = 0 c 1 = 0 e y’(0) = 3 c 1 e 3 t + 3 c 2 te 3 t + c 2 e 3 t = 3 c 1 + c 2 = 2 Então, y = 2 te 3 t c 2 = 2
![Equações não homogêneas método dos coeficientes a determinar Dada a equação não homogênea Ly Equações não homogêneas; método dos coeficientes a determinar Dada a equação não homogênea L[y]](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-18.jpg)
Equações não homogêneas; método dos coeficientes a determinar Dada a equação não homogênea L[y] = y” + p(t)y’ + q(t)y = g(t) onde p, q e g são funções contínuas em um intervalo aberto I. A equação L[y] = y” + p(t)y’ + q(t)y = 0 é chamada de equação homogênea associada. Teorema: Se Y 1 e Y 2 são duas soluções da equação não homogênea acima, então sua diferença Y 1 - Y 2 é uma solução da equação homogênea associada. Se além disso, y 1 e y 2 formam um conjunto fundamental de soluções para a equação homogênea, então Y 1(t) - Y 2(t) = c 1 y 1(t) + c 2 y 2(t), onde c 1 e c 2 são constantes determinadas.

Teorema: A solução geral da equação não homogênea dada poder escrita na forma y = c 1 y 1(t) + c 2 y 2(t) + Y(t), onde y 1 e y 2 formam um conjunto fundamental de soluções da equação homogênea associada, c 1 e c 2 são constantes arbitrárias e Y é alguma solução específica da equação não homogênea. Nota: Por este teorema, devemos fazer 3 coisas para resolver a equação não homogênea dada. 1 - Encontrar a solução geral homogênea associada (yh); c 1 y 1(t) + c 2 y 2(t) da equação 2 – Encontrar uma única solução Y(t) da equação não homogênea (yp); 3 – Somar as duas funções encontradas ( y = yh + yp).

O método dos coeficientes indeterminados Este método requer uma hipótese inicial sobre a forma da solução particular Y(t), mas com os coeficientes não especificados. Substitui-se, então, a expressão hipotética na equação diferencial e tentamos determinar os coeficientes de modo que a equação seja satisfeita. Exemplo: Encontre uma solução particular de y” – 3 y’ – 4 y = 3 e 2 t Solução: Procuramos uma função Y tal que Y”(t) – 3 Y’(t) – 4 Y(t) seja igual a 3 e 2 t. Vamos supor Y(t) = Ae 2 t, onde A deve ser determinado.

Ora, Logo Y’(t) = 2 Ae 2 t e Y’’(t) = 4 Ae 2 t - 6 Ae 2 t - 4 Ae 2 t = 3 e 2 t -6 A = 3, A = - 0, 5 Então, a solução particular é dada por Y(t) = - 0, 5 e 2 t

Tabela de solução particular de ay”+ by’ + c = gi(t) Yi(t) Pn(t) = a 0 tn +a 1 t(n-1)+. . . + an ts (A 0 tn + A 1 t(n-1) +. . . + An) Pn(t) e t ts (A 0 tn + A 1 t(n-1) +. . . + An) e t Pn(t) e t [sen( t)] [cos( t)] ts [(A 0 tn + A 1 t(n-1) +. . . + An) e tcos( t) + ts ( 0 tn + 1 t(n-1) +. . . + n) e tsen( t) Onde s denota o menor inteiro não negativo (s = 0, 1, 2) que garanta que nenhuma parcela de Yi(t) seja solução da equação homogênea correspondente.

Exemplo: Encontre a solução geral da equação diferencial y” – 2 y’ – 3 y = 3 e 2 t. Solução: Temos então a equação característica r 2 – 2 r – 3 = 0 e consequentemente r 1 = 3 e r 2 = -1 Logo yh = c 1 e 3 t + c 2 e –t E a solução particular é dada por y = Ae 2 t, y’ = 2 Ae 2 t, y” = 4 Ae 2 t - 3 Ae 2 t = 3 e 2 t ou A = -1 e yp = - e 2 t Então, como y = yh + yp, temos y = c 1 e 3 t + c 2 e –t - e 2 t

Exemplo: Resolva a equação y” – y’ – 2 y = sen(2 x) Solução: Temos então a equação característica r 2 – r – 2 = 0 e consequentemente r 1 = 2 e r 2 = -1 Logo yh = c 1 e - x + c 2 e 2 x E a solução particular y” – y’- 2 y = sen(2 x) y = A 0 sen(2 x) + 0 cos(2 x), y’ = 2 A 0 cos(2 x) - 2 0 sen(2 x) e y” = - 4 A 0 sen(2 x) - 4 0 cos(2 x), Substituindo em y” – y’ – 2 y = sen(2 x), temos A 0= - 3/20 e 0 = 1/20. Daí a solução y = c 1 e - x + c 2 e 2 x – (3/20) sen(2 x) + (1/20) cos(2 x)

Teorema. Se as funções p, q e g são contínuas em um intervalo aberto I e se as funções y 1 e y 2 são soluções linearmente independentes da equação homogênea associada à equação não homogênea y” + p(t)y’ + q(t)y = g(t), então uma solução particular desta função é e a solução geral é y = c 1 y 1(t) + c 2 y 2(t) + Y(t) como visto antes.

Equações de ordem mais alta Uma equação diferencial linear de ordem n é uma equação da forma P 0(t)dny/dtn + P 1(t)d(n-1)y/dt(n-1) +. . . + Pn-1(t)dy/dt +Pn(t)y =G(t) Supondo que P 0, P 1. . . Pn e G são funções reais e contínuas definidas em algum intervalo I : < t < , e que P 0 nunca se anula nesse intervalo, então dividindo por P 0(t), temos L[y] = dny/dtn +p 1(t)d(n-1)y/dt(n-1) +. . . + pn-1(t)dy/dt+pn(t)y = g(t) Pode-se esperar que para se obter uma única solução, será necessário especificar n condições iniciais y(t 0) = y 0, y’(t 0) = y’ 0, y”(t 0) = y” 0. . . y(n-1)(t 0) = y(n-1)0 Onde t 0 pode ser qualquer ponto de I.

Teorema: Se as funções p 1, p 2, . . . , pn e g são contínuas em I, então existe exatamente uma solução y = (t) da equação diferencial L[y] que também satisfaz as condições iniciais dadas. Essa solução existe em todo o intervalo I. Exemplo: Resolver a equação diferencial y”’ – 6 y”+ 11 y’ – 6 y = 0. Solução: Temos a seguinte equação característica r 3 - 6 r 2 + 11 r – 6 = 0 Logo as raízes são Assim ou (r - 1)(r - 2)(r - 3) = 0. r 1 = 1, r 2 = 2 y = c 1 e t + c 2 e 2 t + c 2 e 3 t. e r 3 = 3.

Teorema. Se as funções p 1, p 2, . . , pn são contínuas no intervalo aberto I, se as funções y 1, y 2, . . , yn são soluções da equação homogênea e se W(y 1, y 2, . . , yn )(t) 0 para, pelo menos um ponto t em I, então toda solução da equação dada pode ser expressa como uma combinação linear das soluções y 1, y 2, . . , yn.
![Equação homogênea com coeficientes constantes Seja a equação Ly a 0 yn a Equação homogênea com coeficientes constantes Seja a equação L[y] = a 0 yn +a](https://slidetodoc.com/presentation_image_h/2161f1b65467d48ccd0dff7b54553ca6/image-29.jpg)
Equação homogênea com coeficientes constantes Seja a equação L[y] = a 0 yn +a 1 y(n-1) +. . . + a(n-1) y’+ any = 0, ai real. A solução, similar ao de segunda ordem é L[e rt] = e rt (a 0 rn +a 1 r(n-1) +. . . + a(n-1) r+ an) = e rt Z(r), onde Z(r) = a 0 rn +a 1 r(n-1) +. . . + a(n-1) r+ an. . Assim podemos escrever a equação característica na forma Z(r) = a 0 (r- r 1) (r- r 2) (r- r 3). . . (r- rn). Se as raízes forem reais e distintas, então temos n soluções diferentes, cujo expressão geral é dada por y = c 1 e r 1 t + c 2 e r 2 t +. . . +cne rnt

Exemplo: Encontre a solução geral de y iv – y = 0, com as condições y(0) = 7/2, y’(0) = 4, y”(0) = 5/2 e y”’(0) = - 2. Temos a equação característica r 4 -1 = 0 ou (r 2 – 1)(r 2 +1) = 0 Donde resulta r 1 = 1, r 2 = - 1, r 3 = i Logo, y = c 1 e t + c 2 e -t + c 3 cost + c 4 sent condições e r 4 = - i. e com as y(0) = c 1 + c 2 + c 3 + 0 = 7/2 y’(0) = c 1 - c 2 - 0 + c 4 = 4, y”(0) = -2 e y”’(0) = -2 Resulta c 1 = 0, c 2 = 3, c 3 = ½ consequentemente a solução y = 3 e -t + (½) cost - sent e c 4 = - 1 e

Exemplo: Encontre a solução geral de yiv +2 y” + y = 0 Neste caso temos a equação característica r 4 + 2 r 2 + 1 = 0 ou (r 2 +1) = 0 cujas raízes são r = i, i, - i. Logo y = c 1 cos t + c 2 sen t + c 3 tcos t + c 4 tsen t. O Método dos coeficientes indeterminados Similar ao de segunda ordem. Exemplo: Encontrar a solução geral de y”’ – 3 y” + 3 y’ – y = 4 et.

Temos a equação característica r 3 - 3 r 2 + 3 r – 1 = 0 = (r - 1) 3. Logo a solução da equação homogênea é y = c 1 e t + c 2 te t + c 3 t 2 e t. Para a solução particular Y(t), vamos supor Y(t) = Ae t. Como e t , te t e homogênea, temos t 2 e t são soluções da equação Y(t) = A t 3 e t. Assim, 6 A e t = 4 e t donde A = 2/3. Portanto, a solução particular é Y(t) = (2/3) t 3 e t e Consequentemente a solução geral y = c 1 e t + c 2 te t + c 3 t 2 e t + (2/3) t 3 e t
 Separação de misturas
Separação de misturas Homogneas
Homogneas Principio da superposição edo
Principio da superposição edo Resposta
Resposta Sistema de segunda ordem
Sistema de segunda ordem Equação diferencial linear
Equação diferencial linear Dot resposta
Dot resposta Edo de 2 ordem
Edo de 2 ordem Tensor de segunda ordem
Tensor de segunda ordem Sistemas lineares escalonamento
Sistemas lineares escalonamento Listas lineares
Listas lineares Equações literais do 2° grau exercicios com respostas
Equações literais do 2° grau exercicios com respostas Superpositionsprinzip
Superpositionsprinzip Equaes
Equaes Desembaraçar de parênteses
Desembaraçar de parênteses Autovalores
Autovalores Sistemas lineares 2 ano ensino médio
Sistemas lineares 2 ano ensino médio Análise de sistemas lineares
Análise de sistemas lineares Equação diferencial
Equação diferencial Lineares gleichungssystem
Lineares gleichungssystem Amplificadores diferenciais
Amplificadores diferenciais Rationale zahlen im alltag
Rationale zahlen im alltag Runge kutta 4 ordem
Runge kutta 4 ordem Nova ordem mundial
Nova ordem mundial Ordem de grandeza
Ordem de grandeza Despistilagem
Despistilagem O estado como garante da ordem liberal
O estado como garante da ordem liberal Familia
Familia Ordem de grandeza
Ordem de grandeza Ordem de ligação
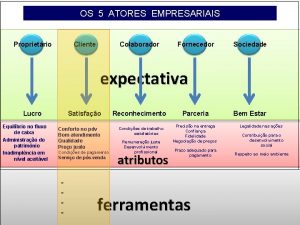
Ordem de ligação Qual a ordem dos atores empresariais
Qual a ordem dos atores empresariais Subnivel mais energetico
Subnivel mais energetico Qual a probabilidade de ser sorteada uma juliana
Qual a probabilidade de ser sorteada uma juliana