lgebra Linear Sistemas de Equaes Lineares Prof Paulo

Álgebra Linear Sistemas de Equações Lineares Prof. Paulo Salgado psgmn@cin. ufpe. br 1

Sumário • Sistemas de Equações Lineares – Sistemas e Matrizes – Operações Elementares – Forma Escada 2

Sistemas de Equações Lineares • Forma 1 de resolução: Suponha o sistema: (I) x 1 + 4 x 2 + 3 x 3 = 1 2 x 1 + 5 x 2 + 4 x 3 = 4 x 1 – 3 x 2 – 2 x 3 = 5 Objetivo: Encontrar o valor de x 1, x 2 e x 3 que satisfazem as três equações ao mesmo tempo. Ou seja…. (1) (2) (3) x 1 = A x 2 = B Ou… x 3 = C 1 2 1 4 5 -3 1 0 0 3 4 -2 0 1 4 5 0 0 1 A B C 3

Sistemas de Equações Lineares Sistemas e Matrizes • Um sistema de equações lineares com m equações e n incógnitas é um conjunto de equações do tipo: a 11 x 1 + a 12 x 2 + … + a 1 nxn a 21 x 1 + a 22 x 2 + … + a 2 nxn … …. … am 1 x 1 + am 2 x 2 + … + amnxn = b 1 = b 2 … = bm com aij, 1 i m, 1 j n, números reais (ou complexos). • Uma solução para esse sistema é a n-upla de números (x 1, x 2, . . . , xn) que satisfaça simultaneamente as m equações. 4
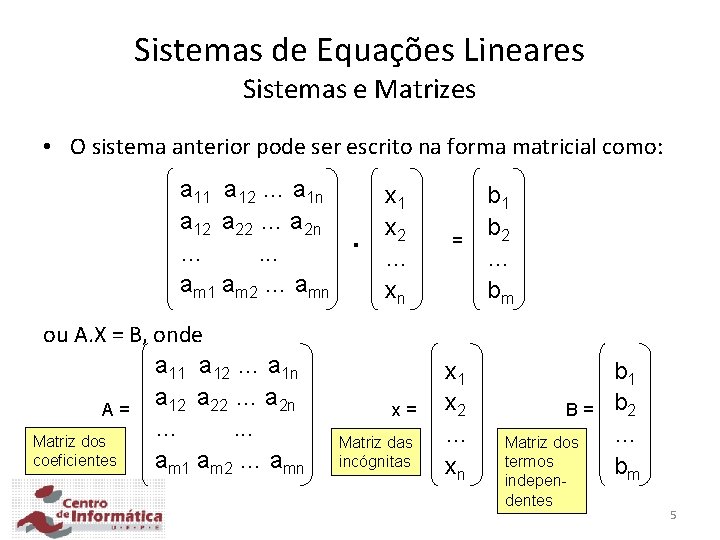
Sistemas de Equações Lineares Sistemas e Matrizes • O sistema anterior pode ser escrito na forma matricial como: a 11 a 12 … a 1 n a 12 a 22 … a 2 n …. . . am 1 am 2 … amn ou A. X = B, onde a 11 a 12 … a 1 n a 12 a 22 … a 2 n A= …. . . Matriz dos coeficientes am 1 am 2 … amn . x 1 x 2 … xn x= Matriz das incógnitas = x 1 x 2 … xn b 1 b 2 … bm B= Matriz dos termos independentes b 1 b 2 … bm 5

Sistemas de Equações Lineares Sistemas e Matrizes • Outra matriz é a chamada matriz ampliada do sistema: a 11 a 12 … a 1 n a 12 a 22 … a 2 n …. . . am 1 am 2 … amn b 1 b 2 … bm 6

Sistemas de Equações Lineares Operações Elementares • São três as operações elementares sobre as linhas de uma matriz § 1) Permuta da i-ésima e j-ésima linhas (Li Lj) • Exemplo: L 2 L 3 1 4 -3 0 -1 4 1 -3 4 0 4 -1 7

Sistemas de Equações Lineares Operações Elementares • São três as operações elementares sobre as linhas de uma matriz § 2) Multiplicação da i-ésima linha por um escalar não-nulo k (Li k. Li) • Exemplo: L 2 -3 L 2 1 4 -3 0 -1 4 1 -12 -3 0 3 4 8

Sistemas de Equações Lineares Operações Elementares • São três as operações elementares sobre as linhas de uma matriz § 3) Substituição da i-ésima linha pela i-ésima linha mais k vezes a jésima linha (Li Li + k. Lj) • Exemplo: L 3 + 2. L 1 1 4 -3 0 -1 4 -1 0 -1 4 9

Sistemas de Equações Lineares • É importante observarmos que usamos apenas operações de multiplicação e adição e permuta de linhas • Assim, todo o processo é reversível • Use o exemplo anterior para mostrar • Os sistemas criados ao longo do processo são ditos equivalentes § Ou seja, a solução para qualquer um deles é solução para o outro 10
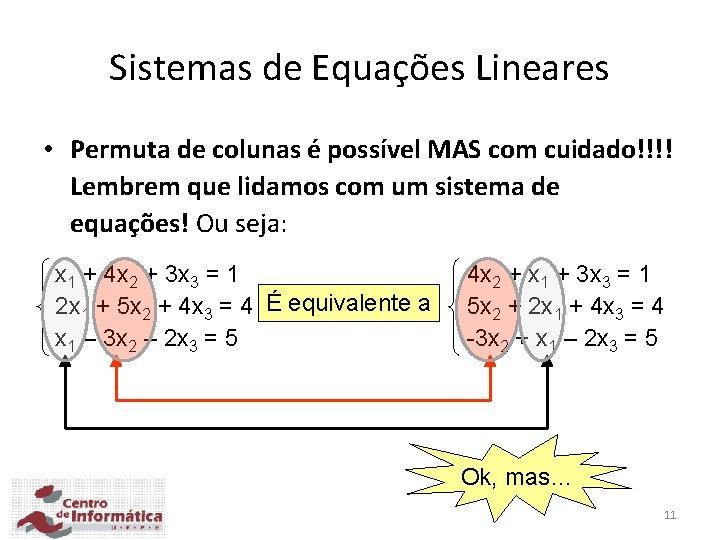
Sistemas de Equações Lineares • Permuta de colunas é possível MAS com cuidado!!!! Lembrem que lidamos com um sistema de equações! Ou seja: x 1 + 4 x 2 + 3 x 3 = 1 2 x 1 + 5 x 2 + 4 x 3 = 4 É equivalente a x 1 – 3 x 2 – 2 x 3 = 5 4 x 2 + x 1 + 3 x 3 = 1 5 x 2 + 2 x 1 + 4 x 3 = 4 -3 x 2 + x 1 – 2 x 3 = 5 Ok, mas… 11

Sistemas de Equações Lineares • Permuta de colunas é possível MAS com cuidado!!!! Lembrem que lidamos com um sistema de equações! Ou seja: x 1 + 4 x 2 + 3 x 3 = 1 NÃO 2 x 1 + 5 x 2 + 4 x 3 = 4 x 1 – 3 x 2 – 2 x 3 = 5 é equivalente a 1 + 4 x 2 + 3 x 3 = x 1 4 + 5 x 2 + 4 x 3 = 2 x 1 5 - 3 x 2 – 2 x 3 = x 1 ERRADO!!!! 12

Sistemas de Equações Lineares Forma Escada • Definição: Uma matriz mxn é linha reduzida à forma escada se: § 1) O primeiro elemento não nulo de uma linha não nula é 1 § 2) Cada coluna que contém o primeiro elemento não nulo de alguma linha tem todos os seus outros elementos iguais a zero § 3) Toda linha nula ocorre abaixo de todas as linhas não nulas (isto é, daquelas que possuem pelo menos um elemento não nulo) § 4) Se as linhas 1, . . . , r são as linhas não nulas, e se o primeiro elemento não nulo da linha i ocorre na coluna ki, então • k 1 < k 2 <. . < kr § Essa condição impõe a forma escada à matriz 13

Sistemas de Equações Lineares Forma Escada • Exemplo 1: 0 0 0 1 0 0 -3 0 0 0 1 0 2 2 0 É forma escada. 14

Sistemas de Equações Lineares Forma Escada • Contra-exemplo 1: 1 0 0 0 1 0 0 -1 1 0 0 0 Não é forma escada pois a segunda condição não é satisfeita: a terceira coluna possui o primeiro elemento não nulo da terceira linha, logo todos os seus outros elementos deveriam ser zero. 15

Sistemas de Equações Lineares Forma Escada • Contra-exemplo 2: 0 1 0 2 0 0 1 -3 0 Não é forma escada pois a primeira e a quarta condições não satisfeitas: 1) O primeiro elemento não nulo de uma linha não nula não é 1 (zero) 2) O primeiro elemento não-nulo da segunda linha deveria estar em uma posição maior do que a do primeiro elemento não-nulo da linha anterior. 16
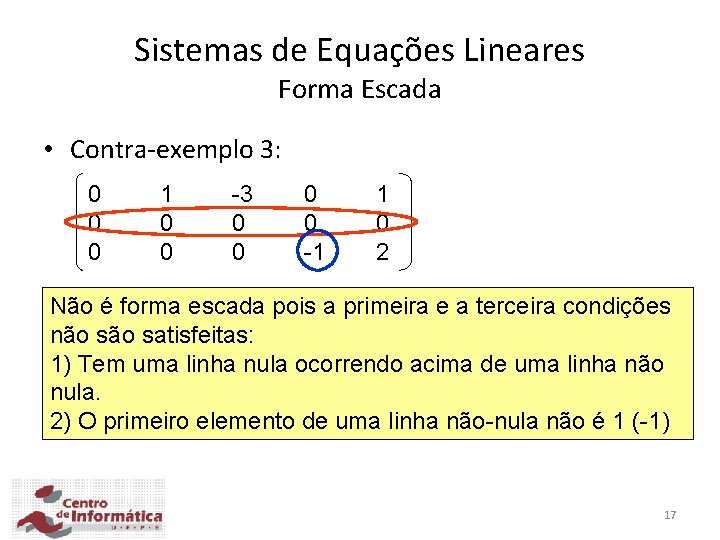
Sistemas de Equações Lineares Forma Escada • Contra-exemplo 3: 0 0 0 1 0 0 -3 0 0 -1 1 0 2 Não é forma escada pois a primeira e a terceira condições não satisfeitas: 1) Tem uma linha nula ocorrendo acima de uma linha não nula. 2) O primeiro elemento de uma linha não-nula não é 1 (-1) 17

Sistemas de Equações Lineares Forma Escada • Teorema: Toda matriz Amxn é linha equivalente a uma única matriz-linha reduzida à forma escada. • Definição: Dada uma matriz Amxn, seja Bmxn a matrizlinha reduzida à forma escada linha equivalente a A. • O posto de A, denotado por p, é o número de linhas não-nulas de B. • A nulidade de A é o número n – p. 18

Sistemas de Equações Lineares Forma Escada • Exemplo: Achar o posto e a nulidade de A: A= 1 -1 1 2 0 -2 1 3 1 0 5 1 19

Sistemas de Equações Lineares Forma Escada • Exemplo: Forma escada de A: 1 -1 1 2 0 -2 1 3 1 0 5 1 L 2=L 1 + L 2 1 0 1 2 2 -2 1 4 1 0 5 1 1 0 0 2 1 -4 1 2 0 0 5/2 1 L 3 = -1. L 1 + L 3 1 0 0 2 2 -4 1 4 0 0 5 1 L 2 = L 2/2 20

Sistemas de Equações Lineares Forma Escada • Exemplo: Forma escada de A: 1 0 0 2 1 -4 1 2 0 0 5/2 1 L 1 = -2. L 2 + L 1 1 0 0 0 1 -4 -3 2 0 -5 5/2 1 1 0 0 0 1 0 -3 2 1 -5 5/2 11/8 L 3 = 4. L 2 + L 3 1 0 0 0 1 0 -3 2 8 -5 5/2 11 L 3 = L 3/8 21

Sistemas de Equações Lineares Forma Escada • Exemplo: Forma escada de A: 1 0 0 0 1 0 -3 2 1 -5 5/2 11/8 L 2 = -2. L 3 + L 2 1 0 0 0 1 0 -3 0 1 -5 -1/4 11/8 L 1 = 3. L 3 + L 1 1 0 0 0 1 -7/8 -1/4 11/8 O posto de A é 3 e a nulidade é 4 – 3 = 1 22

Sistemas de Equações Lineares Forma Escada • Semelhante à resolução de um sistema de equações § Ou seja, dado o sistema: x 1 + 2 x 2 + x 3 = 0 -x 1 + 0 x 2 + 3 x 3 = 5 x 1 – 2 x 2 + x 3 = 1 § A solução é: x 1 = -7/8 x 2 = -1/4 x 3 = 11/8 1 -1 1 2 0 -2 1 3 1 0 5 1 1 0 0 0 1 -7/8 -1/4 11/8 23

Sistemas de Equações Lineares Forma Escada • Exemplo 2: Achar o posto e a nulidade de B: B= 2 1 1 4 -5 16 3 2 1 8 24

Sistemas de Equações Lineares Forma Escada • Exemplo 2: Forma escada de B: 2 1 1 4 -5 16 3 2 1 8 1 0 1 4 4 -9 -5 16 2 -1 1 8 L 2 L 1 L 2= -2. L 1 + L 2 L 3= -1. L 1 + L 3 1 2 1 4 4 -1 -5 16 2 3 1 8 1 0 0 4 4 -9 -9 16 2 -1 -1 8 25

Sistemas de Equações Lineares Forma Escada • Exemplo 2: Forma escada de B: 1 0 0 4 4 -9 -9 16 2 -1 -1 8 1 0 0 0 4 1 -9 0 2 1/9 -1 0 L 4 = -4. L 1 + L 4 L 2= L 2 /-9 L 1= -4. L 2 + L 1 1 0 0 0 4 -9 -9 0 2 -1 -1 0 0 0 0 1 -9 0 14/9 1/9 -1 0 26

Sistemas de Equações Lineares Forma Escada • Exemplo 2: Forma escada de B: 1 0 0 1 -9 0 14/9 1/9 -1 0 L 3 = 9. L 2 + L 3 1 0 0 14/9 1/9 0 0 O posto de B é 2 e a nulidade é 3 – 2 = 1 27

Hoje vimos. . . • Matrizes – Tipos especiais de matrizes – Operações com matrizes • Sistemas de Equações Lineares – Sistemas e Matrizes – Operações Elementares – Forma Escada 28

Álgebra Linear Sistemas de Equações Lineares Prof. Paulo Salgado psgmn@cin. ufpe. br 29

Sumário • Sistemas de Equações Lineares 30

Sistemas de Equações Lineares Soluções • Se tivermos um sistema de uma equação e uma incógnita ax = b, teremos 3 possibilidades: § a 0: neste caso, a equação tem uma única solução • x = b/a § a = 0 e b = 0: temos 0 x = 0 o que significa que qualquer número real é solução da equação § a = 0 e b 0: temos 0 x = b o que significa que não existe solução para essa equação • Vamos analisar o que acontece com sistemas de duas equações e duas incógnitas. . . 31

Sistemas de Equações Lineares Soluções • Exemplo 1: 2 1 2 x 1 + x 2 = 5 x 1 - 3 x 2 = 6 1 -3 5 6 § Precisamos agora passar a matriz reduzida à forma escada L 1 = L 1 / 2 2 1 1 -3 5 6 L 2 = -1. L 1 + L 2 1 0 1/2 -7/2 5/2 7/2 1 0 0 1 3 -1 L 2 = (-2/7). L 2 1 0 1/2 1 5/2 -1 L 1 = (-½). L 2 + L 1 32

Sistemas de Equações Lineares Soluções • Exemplo 1 (cont. ): 2 x 1 + x 2 = 5 x 1 - 3 x 2 = 6 § Assim, o sistema dado tem uma única solução com x 1 = 3 e x 2 = -1 § O posto da matriz de coeficientes reduzidos e o da matriz ampliada é 2 1 0 3 0 1 -1 Matriz de coeficientes reduzidos Matriz ampliada 33

Sistemas de Equações Lineares Soluções • Exemplo 2: 2 x 1 + x 2 = 5 6 x 1 +3 x 2 = 15 2 6 1 3 5 15 § Precisamos agora passar a matriz reduzida à forma escada L 1 = L 1 / 2 2 6 1 3 5 15 L 2 = -6. L 1 + L 2 1 0 1/2 0 5/2 0 § Assim, a segunda equação pode ser ignorada, pois não estabelece condição sobre x 1 ou x 2 34

Sistemas de Equações Lineares Soluções • Exemplo 2 (cont. ): § Assim, para resolver o sistema, consideramos a primeira equação: • 2 x 1 + x 2 = 5 § e, por exemplo, assumimos que x 2 = t § Dessa forma: • x 1 = (5 – t)/2 § Para qualquer valor de t dentro dos reais 35

Sistemas de Equações Lineares Soluções • Exemplo 3: 2 6 2 x 1 + x 2 = 5 6 x 1 + 3 x 2 =10 1 3 5 10 § Precisamos agora passar a matriz reduzida à forma escada L 1 = L 1 / 2 2 6 1 3 5 10 L 2 = -6. L 1 + L 2 1 0 1/2 0 5/2 -5 1 0 1/2 0 0 1 L 2 = L 2/(-5) 1 0 1/2 0 5/2 1 L 1 = (-5/2). L 2 + L 1 36

Sistemas de Equações Lineares Soluções • Exemplo 3 (cont. ): § No caso, tornamos o sistema equivalente a: x 1 + ½x 2 = 0 0 x 1 + 0 x 2 = 1 § Não existe nenhum valor de x 1 e x 2 que satisfaça a segunda equação, assim, o sistema não tem solução § O posto da matriz de coeficientes reduzidos é 1 e o da matriz ampliada é 2 1 0 ½ 0 Matriz de coeficientes reduzidos 1 0 ½ 0 0 1 Matriz ampliada 37

Sistemas de Equações Lineares Soluções – Caso Geral • Consideremos um sistema de m equações lineares com n incógnitas x 1, x 2, . . . , xn a 11 x 1 + a 12 x 2 + … + a 1 nxn a 12 x 1 + a 22 x 2 + … + a 2 nxn … …. … am 1 x 1 + am 2 x 2 + … + amnxn = b 1 = b 2 … = bm • cujos coeficientes aij e termos constantes bi são números reais • Este sistema poderá ter: 38

Sistemas de Equações Lineares Soluções – Caso Geral • i) Uma única solução § Sistema possível (compatível) e determinado • ii) Infinitas soluções § Sistema possível (compatível) e indeterminado • iii) Nenhuma solução § Sistema impossível (incompatível) 39

Sistemas de Equações Lineares Soluções – Caso Geral • Teorema: § i) Um sistema de m equações e n incógnitas admite solução se, e somente se, o posto da matriz ampliada é igual ao posto da matriz dos coeficientes § ii) Se as duas matrizes têm o mesmo posto p e p = n (número de incógnitas), então a solução será única (Ex. I) § iii) Se as duas matrizes têm o mesmo posto p e p < n, então podemos escolher n – p incógnitas, as outras p incógnitas serão dadas em função dessas (Ex. III) • O grau de liberdade do sistema é n - p 40

Sistemas de Equações Lineares Soluções – Caso Geral • Seja: § pc = Posto da matriz dos coeficientes § pa = Posto da matriz ampliada § Se pc = pa, chamaremos de p § m e n são as dimensões da matriz de coeficientes • m equações com n incógnitas 41

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 1: 1 0 0 0 1 3 -2 2 pc = p a = 3 m = 3, n = 3 e p = 3 Logo, o sistema admite uma única solução. 42

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 2: 1 0 0 1 7 5 -10 -6 pc = p a = 2 m = 2, n = 3 e p = 2 Logo, o sistema tem grau de liberdade 1. 43

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 3: 1 0 0 0 1 0 7 5 0 0 0 1 pc = 2, pa = 3 m = 3, n = 3 Logo, o sistema é impossível e não tem solução. 44

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 4: 1 0 0 0 1 0 -10 7 0 -2 1 0 -10 4 0 pc = p a = 2 m = 3, n = 4 e p = 2. Temos dois graus de liberdade. 45

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 5: Vamos resolver o sistema x + 2 y + z + t = 0 x + 3 y – z + 2 t = 0 1 1 2 3 1 -1 1 2 0 0 5 -2 -1 1 0 0 L 2 = -1. L 1 + L 2 1 0 2 1 1 -2 1 1 L 1 = -2. L 2 + L 1 0 0 1 46

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 5 (cont. ): § Assim, o sistema tem duas variáveis livres (grau de liberdade 2) • zet § Logo, se fixarmos os valores de z e t teremos: • x = -5 z + t • y = 2 z - t 47

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 6: Vamos resolver o sistema x + 3 y + z = 0 2 x + 6 y + 2 z = 0 -x – 3 y – z = 0 1 2 -1 3 6 -3 1 2 -1 0 0 0 L 2 = -2. L 1 + L 2 L 3 = L 1 + L 3 1 0 0 3 0 0 1 0 0 0 48

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 6 (cont. ): § Novamente, o sistema tem duas variáveis livres (grau de liberdade 2) • yez § Logo, se fixarmos os valores de y e z teremos: • x = -3 y - z 49

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 7: Vamos resolver o sistema x + 2 y + z + t = 1 x + 3 y – z + 2 t = 3 1 1 2 3 1 -1 1 2 1 3 5 -2 -1 1 -3 2 L 2 = -1. L 1 + L 2 1 0 2 1 1 -2 1 1 L 1 = -2. L 2 + L 1 1 2 1 0 0 1 50

Sistemas de Equações Lineares Soluções – Caso Geral • Exemplo 7 (cont. ): § Novamente, duas variáveis livres (grau de liberdade 2) • zet § Logo, se fixarmos os valores de z e t teremos: • x = -5 z + t - 3 • y = 2 z – t + 2 51

Hoje vimos. . . • Sistemas de Equações Lineares 52

Exercícios Sugeridos • 10 a 16 53

A Seguir… • Determinantes e Matriz Inversa 54 R A I L R B L Á N A G E E
- Slides: 54