Sistemas de equaes lineares de 1 a ordem







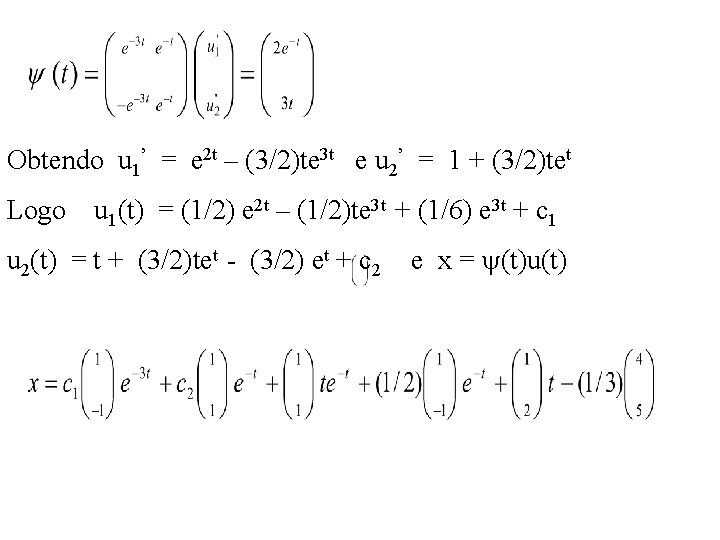








- Slides: 16

Sistemas de equações lineares de 1 a ordem Sistemas de equações diferenciais simultâneas aparecem naturalmente em problemas envolvendo diversas variáveis dependentes, cada uma das quais sendo uma função de uma única variável dependente. A variável independente será denotada por t e as dependentes por x 1 , x 2 , . . Serão vistos os sistemas de duas ou mais equações diferenciais que sempre podem ser escritas como equações de primeira ordem. Para transformar uma equação arbitrária de ordem n y(n) = F(t, y, y’, y”, . . . , y(n-1)) em um sistema de equações de primeira ordem, definimos as variáveis x 1 , x 2 , . . . , xn por x 1 = y, x 2 = y’, . . . , xn = y(n-1).

Para transformar uma equação arbitrária de ordem n y(n) = F (t, y’, y”, . . . , y(n-1)) em um sistema de equações de primeira ordem, definimos as variáveis x 1, x 2, . . . , xn por x 1 = y, x 2 = y’, . . . , xn = y(n-1). Segue imediatamente que , x’ 1 = x 2, x’ 2 = x 3, . . . , x’n-1 = xn, ou seja x’n = F (t, x 1, x 2, , . . . , xn). O caso mais geral, temos: x’ 1 = F 1 (t, x 1, x 2, , . . . , xn) x’ 2 = F 2 (t, x 1, x 2, , . . . , xn). . . . . x’n = F 1 (t, x 1, x 2, , . . . , xn).

Dizemos que este sistema tem uma solução em I : < t < Se existe um conjunto de n equações x 1 = 1(t), x 2 = 2(t), . . . , xn = n(t) diferenciáveis em todo I e que satisfazem o sistema dado e podendo ainda constar as condições iniciais da forma x 1(t 0) = x 10, x 2(t 0) = x 20 , . . . , xn(t 0) = xn 0, onde to é um valor especificado de t em I e x 10, x 20 , . . . , xn 0 são números dados. Se as funções F 1, F 2, . . . , Fn são lineares das variáveis dependentes x 1, x 2 , . . . , xn, então o sistema é dito linear; caso contrário, é não-linear. Assim, o sistema mais geral de n equações lineares tem a forma

x 1’ = p 11(t)x 1 + p 12(t)x 2 +. . . + p 1 n(t)xn + g 1(t) x 2’ = p 21(t)x 1 + p 22(t)x 2 +. . . + p 2 n(t)xn + g 2(t). . . . . xn’ = pn 1(t)x 1 + pn 2(t)x 2 +. . . + pnn(t)xn + gn(t) Se todas as g 1, g 2, . . . , gn forem identicamente nulas em I, então o sistema é dito homogêneo; caso contrário, ele é nãohomogêneo. Teorema: Se as funções p 11, p 12, . . . pnn, g 1, g 2, . . . , gn são contínuas em um intervalo aberto I : < t < , então existe uma única solução x 1 = 1(t), x 2 = 2(t), . . . , xn = n(t), do sistema acima que também satisfaz as condições iniciais onde t 0 é qualquer ponto em I e x 10, x 20 , . . . , xn 0 são números arbitrários. Além disso, a solução existe em todo o intervalo I.

Exemplo: Transforme a equação dada em um sistema de equações de primeira ordem u” + 0, 5 u’ + 2 u = 0. Solução: x 1 = u, x 2 = u’. Logo obtemos x 2’ + 0, 5 x 2 + 2 x 1 = 0 x 1’ = x 2’ = -2 x 1 – 0, 5 x 2 x 1’ = x 2 e como u” = x 2’, ou seja

Sistemas de equações diferenciais ordinárias Considere o método de variação de parâmetro x’ = P(t)x + g(t) seja (t) uma matriz fundamental para o sistema x’ = P(t)x. Como solução geral do sistema é (t)c temos x = (t) u(t) onde u(t) é uma função vetorial em lugar de c. Assim, ’(t) u(t) + (t) u’(t) = P(t) u(t) + g(t) Como (t) é uma matriz fundamental, ’(t) = P(t) Logo resulta em (t) u’(t) = g(t) donde (t) u’(t) = -1(t )g(t) Assim podemos selecionar como u(t) qualquer vetor na classe de vetores que satisfaz esta equação.

Portanto, u(t) = -1(s)g(s)ds + c Logo, x = (t)c + (t) -1(s)g(s)ds que é a solução do sistema inicial. Exemplo: Determine a solução do sistema A solução geral deste sistema homogêneo é e a matriz fundamental x = (t)u(t), onde u(t) satisfaz (t)u’(t) = g(t), ou
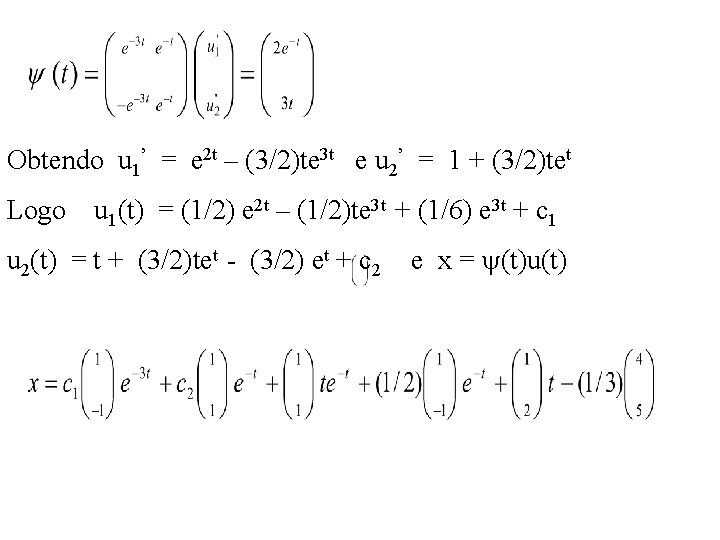
Obtendo u 1’ = e 2 t – (3/2)te 3 t e u 2’ = 1 + (3/2)tet Logo u 1(t) = (1/2) e 2 t – (1/2)te 3 t + (1/6) e 3 t + c 1 u 2(t) = t + (3/2)tet - (3/2) et + c 2 e x = (t)u(t)

Autovalores e autovetores: Sejam os sistemas Ax = y (1) e Ax = x (2), fator de proporcionalidade, onde y = x. Assim podemos escrever (A - I)x = 0. Esta equação possui soluções não nulas se e somente se for escolhido de modo que det(A - I) = 0. Os valores de são chamados autovalores de A e as soluções não nulas das equações (1) e (2) obtidas usando um tal valor de são chamadas autovetores. Exemplo: Determine todos os autovalores e autovetores de

Solução: Como (A - I)x = 0, temos Ou seja, (5 - ) (1 - ) + 3 = 0 e consequentemente 1 = 2 e 2 = 4 são os autovalores procurados. Determinando os autovetores. Para 1 = 2

Se x 1 = c, como x 2 = 3 x 1, temos Onde x(1) é um autovetor de A. Similarmente, para 2 = 4, temos Logo, x(2) um autovetor de A. x 2 = 3 c. Logo

Teoria básica de sistemas de equações lineares Considere o sistemas na forma: x 1’ = p 11(t)x 1 + p 12(t)x 2 +. . . + p 1 n(t)xn + g 1(t) x 2’ = p 21(t)x 1 + p 22(t)x 2 +. . . + p 2 n(t)xn + g 2(t). . . . . xn’ = pn 1(t)x 1 + pn 2(t)x 2 +. . . + pnn(t)xn + gn(t) Ou seja, x’ = P(t)x + g(t) As homogêneas x’ = P(t)x, g(t) = 0. (3)

Tal que xij(k) = xij(k) denota a a i-ésima componente da jésima solução x(j)(t). Teorema: Se as funções vetoriais x(1) e x(2) são soluções do sistema x’ = P(t)x, g(t) = 0, então a combinação linear c 1 x(1) + c 2 x(2) também é solução quaisquer que sejam as constantes c 1 e c 2. . Como consequencia deste teorema temos que, se x(1) , x(2) , . . . , x(k) são soluções de x’ = P(t)x então x = c 1 x(1)(t) + c 2 x(2)(t) +. . . + ckx(k) também é solução quaisquer sejam as constantes c 1, c 2 , . . . , ck

Sistemas lineares homogêneo com coeficientes constantes Consideremos o sistema na forma x’ = Ax, A é uma matriz 1 xn (1). Se n =1, o sistema fica dx / dt = ax cuja solução é x = ceat. Para determinar a solução de x’ = Ax, procedemos como para equação da segunda ordem, isto é, procuramos soluções da forma x = ert onde r é um vetor constante e deve ser determinado. Assim, temos r ert = A ert ou A = r. Logo, (A – r. I) = 0, onde I é a matriz identidade nxn. Isto significa dizer que para resolver o sistema de equações diferenciais (1) precisamos resolver os sistema algébrico (A – r. I) = 0 que consiste em encontrar os autovalores e os autovetores da matriz A.

Exemplo: Considere o sistema temos Logo, para r 1 = 3, temos - 2 1 + 2 = 0 2 = 2 1 donde

Para r 2 = -1, temos 2 1 + 2 = 0 2 = - 2 1 donde Então x = c 1 x(1)(t) + c 2 x(t) Ou c 1 e c 2 constantes.
 Análise de sistemas lineares
Análise de sistemas lineares Regra de cramer
Regra de cramer Sistemas lineares escalonamento
Sistemas lineares escalonamento Como resolver equações literais
Como resolver equações literais Desembaraçar de parênteses
Desembaraçar de parênteses Equação diferencial
Equação diferencial Equaes
Equaes Regelungstechnik
Regelungstechnik Lineares gleichungssystem
Lineares gleichungssystem Anwendung pythagoras alltag
Anwendung pythagoras alltag Listas lineares
Listas lineares Difmos
Difmos Transformações lineares
Transformações lineares Algarismos significativos
Algarismos significativos Runge kutta 4 ordem
Runge kutta 4 ordem Nova ordem mundial
Nova ordem mundial Banana bot
Banana bot