Signature Schemes Part II 1 Outline n n

![Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-2.jpg)
![[4] Variants of the El. Gamal Signature Scheme (1) Schnorr Signature Scheme n n [4] Variants of the El. Gamal Signature Scheme (1) Schnorr Signature Scheme n n](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-3.jpg)











![[5] Signatures with additional functionality (1) Blind signature schemes (1983) (2) Undeniable signature schemes [5] Signatures with additional functionality (1) Blind signature schemes (1983) (2) Undeniable signature schemes](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-15.jpg)




















- Slides: 38

Signature Schemes (Part II) 1
![Outline n n 1 2 3 4 n n Introduction Security Requirements for Signature Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-2.jpg)
Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature Schemes The El. Gamal Signature Scheme Variants of the El. Gamal Signature Scheme The Schnorr Signature Scheme The Digital Signature Algorithm The Elliptic Curve DSA [5] Signatures with additional functionality n n n Blind Signatures Undeniable Signatures Fail-stop Signatures 2
![4 Variants of the El Gamal Signature Scheme 1 Schnorr Signature Scheme n n [4] Variants of the El. Gamal Signature Scheme (1) Schnorr Signature Scheme n n](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-3.jpg)
[4] Variants of the El. Gamal Signature Scheme (1) Schnorr Signature Scheme n n Proposed in 1989 Greatly reduced the signature size (2) Digital Signature Algorithm (DSA) n n Proposed in 1991 Was adopted as a standard on December 1, 1994 (3) Elliptic Curve DSA (ECDSA) n FIPS 186 -2 in 2000 3

(1) Schnorr Signature Scheme Let p be a prime such that the DL problem in Zp* is intractable, and let q be a prime that divides p-1. Let α be a qth root of 1 modulo p. Define K={ (p, q, α, a, β): β=αa mod p } p, q, α, β are the public key, a is private 4

n n For a (secret) random number k, define sig(x, k)=(γ, δ), where γ=hash(x||αk ) andδ=k+aγ mod q For a message (x, (γ, δ)), verification is done by performing the following computations: ver(x, (γ, δ))=true iff. hash(x||αδβ-γ)=γ 5

n If the signature was construct correctly, the verification will succeed since αδβ-γ=αk+aγα-aγ=αk 6

(Schnorr Signature Scheme Example) n n We take q=101, p=78 q+1=7879, α=170, a=75, then β=17075 mod 7879=4567 To sign the message m=15, Alice selects k=50; Then γ=hash(15||17050), δ=5+75*γ mod 101 (15, (γ, δ)) is the signed message 7

L=0 mod 64, 512≤L≤ 1024 (2) Digital Signature Algorithm n Let p be a L-bit prime such that the DL problem in Zp* is intractable, and let q be a 160 -bit prime that divides p-1. Let α be a qth root of 1 modulo p. Define K={ (p, q, α, a, β): β=αa mod p } p, q, α, β are the public key, a is private 8

n n For a (secret) random number k, define sig (x, k)=(γ, δ), where γ=(αk mod p) mod q and δ=(SHA-1(x)+aγ)k-1 mod q For a message (x, (γ, δ)), verification is done by performing the following computations: e 1=SHA-1(x)*δ-1 mod q e 2=γ*δ-1 mod q ver(x, (γ, δ))=true iff. (αe 1βe 2 mod p) mod q=γ 9

n Notice that the verification requires to compute: e 1=SHA-1(x)*δ-1 mod q e 2=γ*δ-1 mod q when δ=0 (it is possible!), Alice should reconstruct a new signature with a new k 10

(DSA Example) n n Take q=101, p=78 q+1=7879, α=170, a=75; then β=4567 To sign the message SHA-1(x)=22, Alice selects k=50; Then γ=(17050 mod 7879) mod 101=94, δ=(22+75*94)50 -1 mod 101=97 (x, (94, 97)) is the signed message 11

n The signature (94, 97) on the message digest 22 can be verify by the following computations: δ-1=97 -1 mod 101=25 e 1=22*25 mod 101=45 e 2=94*25 mod 101=27 (17045*456727 mod 7879) mod 101 = 94 =γ 12

(3) Elliptic Curve DSA n Let p be a prime or a power of two, and let E be an elliptic curve defined over Fp. Let A be a point on E having prime order q, such that DL problem in <A> is infeasible. Define K={ (p, q, E, A, m, B): B=m. A } p, q, E, A, B are the public key, m is private 13

n n For a (secret) random number k, define sig (x, k)=(r, s), where k. A=(u, v), r=u mod q and s=k-1(SHA-1(x)+mr) mod q For a message (x, (r, s)), verification is done by performing the following computations: i=SHA-1(x)*s-1 mod q j=r*s-1 mod q (u, v)=i. A+j. B ver(x, (r, s))=true if and only if u mod q=r 14
![5 Signatures with additional functionality 1 Blind signature schemes 1983 2 Undeniable signature schemes [5] Signatures with additional functionality (1) Blind signature schemes (1983) (2) Undeniable signature schemes](https://slidetodoc.com/presentation_image_h2/6ad015aa60318774547d0c4dc5b8c81e/image-15.jpg)
[5] Signatures with additional functionality (1) Blind signature schemes (1983) (2) Undeniable signature schemes (1989) (3) Fail-stop signature schemes (1992) 15

(1) Blind signature schemes n n A sends a piece of information to B which B signs and returns to A. From this signature, A can compute B’s signature on an a priori message x of A’s choice (B is a signer here!) B knows neither the message x nor the signature associated with it 16

Chaum’s blind signature protocol (1983) (A is a sender and B is a signer, (n, e) is RSA public key of B and d is RSA private key of B) 1. A randomly selects a secret integer k 2. A computes x*= xke mod n and sends it to B 3. B computes y*= (x*)d mod n and sends it to A 4. A computes y= k-1 y* mod n, which is B’s signature on x (Note the signer B does not know (x, y) but (x, y) is a B’s signed message. ) 17

(An application of the blind signature) n The sender A (the customer) does not want the signer B (the bank) to know a message x and its signature y. This may be important in e-cash applications where a message x might represent a monetary value which A can spend. When x and y are presented to B for payment, B is unable to deduce which party was originally given the signed value. This allows A to remain anonymous so that spending patterns cannot be monitored. 18

(2) Undeniable Signatures n n n A signature can not be verified without the cooperation of the signer First introduced by Chaum and van Antwerpen in 1989 Protects Alice against the possibility that documents signed by her are duplicated and distributed electronically without her approval 19

n n Since a signature should be verified with the cooperation of the signer, it is possible for a signer to evilly disavow a signature which signed by him previously An undeniable signature scheme should consists of a disavowal protocol between the verifier B and the signer A, such that: n n For a signature which is not signed by A, B will recognize it as a forgery For a signature which is signed by A, A can fool B to recognized it as a forgery with very low probability 20

(An application of the undeniable signature) n A large corporation A creates a software package. A signs the package and sells it to B, who decides to make copies of this package and resell it to a third party C. C is unable to verify the authenticity of the software without the cooperation of A 21

Chaum-van Antwerpen undeniable signature scheme n Let p=2 q+1 be a prime such that q is prime And the DL problem in Zp is intractable. Let α be an element of order q. Define: K={ (p, α, a, β) : β=αa mod p } 1. Signing algorithm n To sign a message x, Alice computes y=sig(x)=xa mod p 22

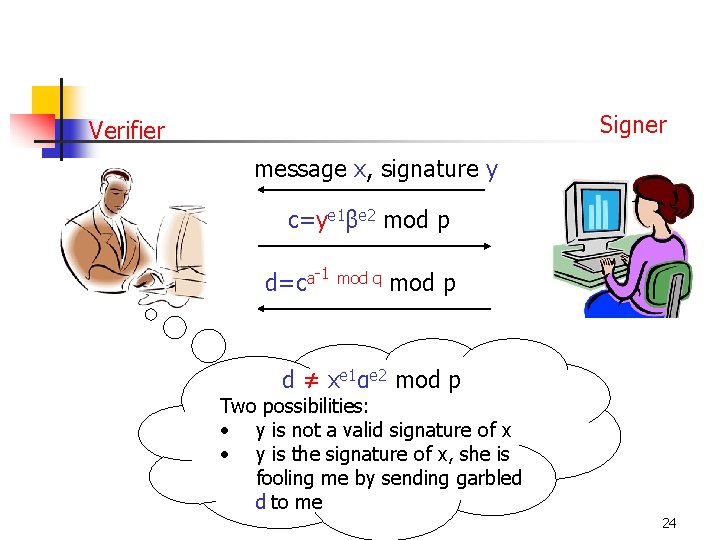
2. Verification protocol n Bob chooses e 1, e 2 from Zq* randomly e e n Bob computes c=y 1β 2 mod p and sends it to Alice -1 mod q a n Alice computes d=c mod p and sends it to Bob n Bob accepts s as a valid signature if and only if d = xe 1αe 2 mod p 23

Signer Verifier message x, signature y c=ye 1βe 2 mod p d=ca-1 mod q mod p d ≠ xe 1αe 2 mod p Two possibilities: • y is not a valid signature of x • y is the signature of x, she is fooling me by sending garbled d to me 24

(Correctness of the signature protocol) n Bob will accept a valid signature, since if y is valid: y=xa mod p, then c = ye 1βe 2 = xae 1αae 2 mod p Hence d = xe 1αe 2 mod p as desired 25

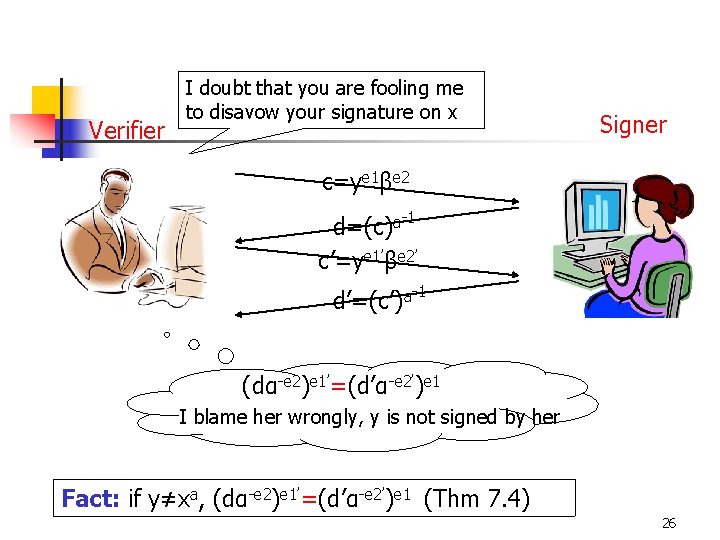
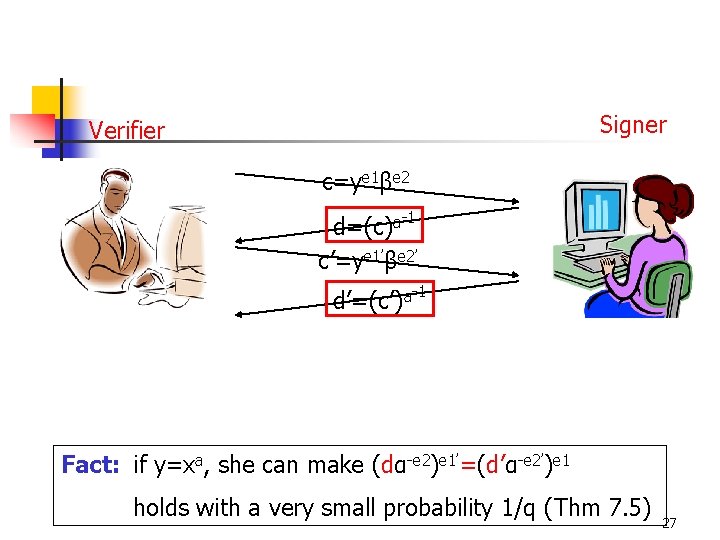
Verifier I doubt that you are fooling me to disavow your signature on x Signer c=ye 1βe 2 d=(c)a-1 c’=ye 1’βe 2’ d’=(c’)a-1 (dα-e 2)e 1’=(d’α-e 2’)e 1 I blame her wrongly, y is not signed by her Fact: if y≠xa, (dα-e 2)e 1’=(d’α-e 2’)e 1 (Thm 7. 4) 26

Signer Verifier c=ye 1βe 2 d=(c)a-1 c’=ye 1’βe 2’ d’=(c’)a-1 Fact: if y=xa, she can make (dα-e 2)e 1’=(d’α-e 2’)e 1 holds with a very small probability 1/q (Thm 7. 5) 27

3. Disavowal protocol (1/3) B selects random secret integers e 1, e 2 and computes c=ye 1βe 2 mod p, and sends c to A A computes -1 a d=(c) mod p and sends d to B B checks if d=xe 1αe 2, then he concludes that y is a valid signature of x, otherwise go to next step 28

Disavowal protocol (2/3) B selects random secret integers e 1’, e 2’ and computes c’=ye 1’βe 2’ mod p, and sends c’ to A A computes -1 a d’=(c’) mod p and sends d’ to B B checks if d’=xe 1’αe 2’, then he concludes that y is a valid signature of x, otherwise go to next step 29

Disavowal protocol (3/3) B checks (dα-e 2)e 1’=(d’α-e 2’)e 1 if it holds, he concludes that y is a forgery Otherwise, he concludes that A is trying to disavow the signature 30

Fact Let x be a message and suppose that y is A’s (purported) signature on x n n If y is a forgery, i. e. , y≠xa mod p, then (dα-e 2)e 1’=(d’α-e 2’)e 1 holds Suppose that y is indeed A’s signature for x, i. e. , y=xa mod p, then (dα-e 2)e 1’=(d’α-e 2’)e 1 holds with probability 1/q 31

(3) Fail-stop Signatures n n In a fail-stop signature scheme, when Oscar is able to forge Alice’s signature on a message, Alice will (with high probability) be able to prove that Oscar’s signature is a forgery A fail-stop signature scheme consists of a singing algorithm, a verification algorithm and a “proof of forgery” algorithm 32

Van Heyst and Pedersen scheme (1992) (a one time signature scheme) n n n Let p=2 q+1 be a prime such that q is prime and the DL problem in Zp is intractable. Let α be an element of order q. Let 1≤a 0≤q-1 and define β=αa 0 mod p. The value of a 0 is kept secret from everyone The values p, q, α, β and a 0 are chosen by a trusted central authority 33

n A key has the form K=(γ 1, γ 2, a 1, a 2, b 1, b 2) where γ 1=αa 1βa 2 mod p γ 2=αb 1βb 2 mod p (γ 1, γ 2) is the public key and (a 1, a 2, b 1, b 2) is private 34

n To sign a message x, sig(x)=(y 1, y 2) where y 1=a 1+xb 1 mod q y 2=a 2+xb 2 mod q To verify a signed message (x, (y 1, y 2)) ver(x, (y 1, y 2))=true iff. γ 1γ 2 x =αy 1βy 2 mod p n 35

Proof of forgery – the argument n n If there is a signature (y 1’’, y 2’’) on a message x’ which can be verified as signing by Alice, but actually it is not signed by Alice, i. e. (y 1’’, y 2’’)≠sig(x’) then Alice can calculate the secret a 0 which was not given to her Alice shows a 0 to prove that she is innocent 36

Proof of forgery – calculation of a 0 n n Since (y 1’’, y 2’’) is a valid signature on x’ γ 1γ 2 x’ =αy 1’’βy 2’’ mod p Alice can compute her own signature (y 1’, y 2’) on x’ γ 1γ 2 x’ =αy 1’βy 2’ mod p Hence αy 1’’βy 2’’=αy 1’βy 2’ mod p αy 1’’αa 0 y 2’’=αy 1’αa 0 y 2’ mod p 37

Thus y 1’’+a 0 y 2’’=y 1’+a 0 y 2’ (mod q) a 0=(y 1’’-y 1’)(y 2’-y 2’’)-1 (mod q) It is computable by Alice! 38
 What is sentence outline
What is sentence outline Middle punt return scheme
Middle punt return scheme Rhyme scheme
Rhyme scheme Rhyming scheme
Rhyming scheme Microorganisms definition
Microorganisms definition Punt block schemes
Punt block schemes Tricolon
Tricolon Organization schemes
Organization schemes Signal encoding schemes
Signal encoding schemes Mouse in afrikaans
Mouse in afrikaans Slsam
Slsam What is repetition in poetry
What is repetition in poetry Three generations of multicomputers
Three generations of multicomputers Food assurance schemes
Food assurance schemes Filling schemes
Filling schemes Scheme stata
Scheme stata J384/02 mark scheme
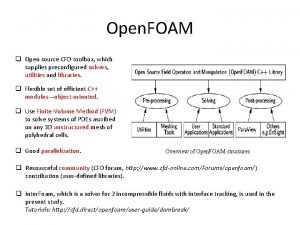
J384/02 mark scheme Swak4foam
Swak4foam Schemes in piaget's theory
Schemes in piaget's theory Color theory for kids
Color theory for kids Rhyme scheme
Rhyme scheme Product classification schemes
Product classification schemes Restricted extremity wristband
Restricted extremity wristband Blue adjective
Blue adjective Pilot relaying schemes
Pilot relaying schemes Jaggled
Jaggled Information architecture organization schemes
Information architecture organization schemes Register disbursement scheme
Register disbursement scheme Classification schemes
Classification schemes Free verse poem meaning
Free verse poem meaning Schools recommendation schemes
Schools recommendation schemes New and navigation schemes selection of window
New and navigation schemes selection of window Consaa
Consaa Wecs schemes
Wecs schemes Standards rhyme
Standards rhyme Split complementary color scheme
Split complementary color scheme Packaging color schemes
Packaging color schemes Basic color schemes
Basic color schemes Ap seminar part b outline
Ap seminar part b outline