Chapter 7 1 Signature Schemes 1 Outline n

![Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-2.jpg)
![[1] Introduction n n A signature scheme consists of two components: a signing algorithm [1] Introduction n n A signature scheme consists of two components: a signing algorithm](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-3.jpg)
![n [Def] A signature scheme is a 5 -tuple (P, A, K, S, V): n [Def] A signature scheme is a 5 -tuple (P, A, K, S, V):](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-4.jpg)



![[2] Security Requirements for Signature Schemes n Three attack models n Key-only attack Oscar [2] Security Requirements for Signature Schemes n Three attack models n Key-only attack Oscar](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-9.jpg)








![[3] El. Gamal Signature Scheme n El. Gamal Signature Scheme was proposed in 1985 [3] El. Gamal Signature Scheme n El. Gamal Signature Scheme was proposed in 1985](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-18.jpg)


















- Slides: 37

Chapter 7 -1 Signature Schemes 1
![Outline n n 1 2 3 4 n n Introduction Security Requirements for Signature Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-2.jpg)
Outline n n [1] [2] [3] [4] n n Introduction Security Requirements for Signature Schemes The El. Gamal Signature Scheme Variants of the El. Gamal Signature Scheme The Schnorr Signature Scheme The Digital Signature Algorithm The Elliptic Curve DSA [5] Signatures with additional functionality n n n Blind Signatures Undeniable Signatures Fail-stop Signatures 2
![1 Introduction n n A signature scheme consists of two components a signing algorithm [1] Introduction n n A signature scheme consists of two components: a signing algorithm](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-3.jpg)
[1] Introduction n n A signature scheme consists of two components: a signing algorithm and a verification algorithm Alice can sign a message x using a private signing algorithm sig The resulting signature sig(x) can subsequently be verified using a public verification algorithm ver Given a pair (x, y), the verification algorithm returns an answer “true” or “false” depending on whether the signature is valid. 3
![n Def A signature scheme is a 5 tuple P A K S V n [Def] A signature scheme is a 5 -tuple (P, A, K, S, V):](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-4.jpg)
n [Def] A signature scheme is a 5 -tuple (P, A, K, S, V): n n P is a finite set of possible messages A is a finite set of possible signatures K is a finite set of possible keys For each key K, there is a signing algorithm sigk in S and a verification algorithm verk in V such that: n n ver(x, y) = true if and only if y=sig(x) A pair (x, y) is a signed message 4

n n n The functions sigk and verk should be polynomial-time computable functions Given a message x, it should be computationally infeasible for anyone other than Alice to compute a signature y such that verk(x, y)=true If Oscar can compute a pair (x, y) such that verk(x, y)=true and x was not previously signed by Alice, y is called a forgery 5

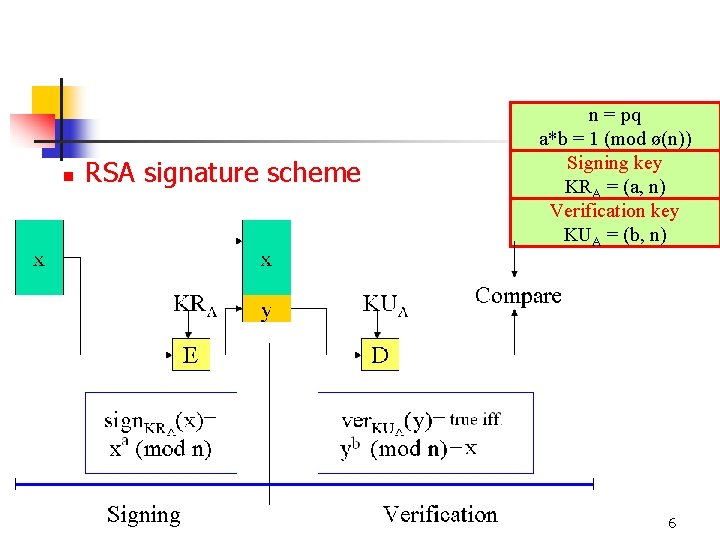
n RSA signature scheme n = pq a*b = 1 (mod ø(n)) Signing key KRA = (a, n) Verification key KUA = (b, n) 6

(RSA signature scheme) n Let n=pq, p and q are primes. Define K={ (n, p, q, a, b) : n=pq, ab=1 mod phi(n) } n For each K=(n, p, q, a, b) in K, define y = sig. K(x) = xa mod n and ver. K(x, y) = true if and only if x = yb mod n 7

1. Combine signing and encryption Signing before encrypting is recommended. Since: if Alice first encrypted m, then signed the result: z=e. Bob(x) and y=sig. Alice(z) Oscar can replace y by his own signature y’=sig. Oscar(z) Bob may infer that the plaintext x originated with Oscar. 8
![2 Security Requirements for Signature Schemes n Three attack models n Keyonly attack Oscar [2] Security Requirements for Signature Schemes n Three attack models n Key-only attack Oscar](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-9.jpg)
[2] Security Requirements for Signature Schemes n Three attack models n Key-only attack Oscar possesses Alice’s public key n Known message attack Oscar possesses a list of messages previously signed by Alice n Chosen message attack Oscar requests Alice’s signatures on a list of messages 9

n Three possible adversarial goals n Total break Determine the signing key n Selective forgery Forge a valid signature on a message chosen by someone else with non-negligible probability n Existential forgery Forge a valid signature on a message which hasn’t previously been signed by Alice 10

Forgeries Based on RSA Signature Scheme n n n Existential forgery using a key-only attack Existential forgery using a known message attack Selective forgery using a chosen message attack 11

n Existential forgery using a key-only attack For any y, (x=yb, y) satisfies verk(x, y) = true The use of hash functions in conjunction with signature schemes will eliminate this type of forging 12

n Existential forgery using a known message attack The attack is based on the multiplicative property of RSA. Suppose y 1=sigk(x 1), y 2=sigk(x 2) are two messages previously signed by Alice. Then verk(x 1 x 2 mod n, y 1 y 2 mod n)=true 13

n n Selective forgery using a chosen message attack Suppose Oscar wants to forge a signature on the message x, where x was possibly chosen by someone else. It is simple matter for him to find x 1, x 2 in Zn such that x=x 1 x 2 mod n He asks Alice for het signatures on messages x 1 and x 2, which we denote by y 1 and y 2 respectively As in previous attack, y 1 y 2 mod n is the signature for the message x=x 1 x 2 mod n 14

Three attacks related to hash in signature scheme 1. Oscar may start with a valid signed message (x, y), where y=sig. Alice(h(x)). Then he computes z=h(x) and attempts to find x’≠x such that h(x’)=h(x). If Oscar can do this, (x’, y) would be a valid signed message In order to prevent this type of attack, we require that h is second preimage resistant 15

2. Oscar first finds two messages x’≠x such that h(x)=h(x’). Oscar them gives x to Alice and persuades her to sign the message digest h(x), obtaining y. If Oscar can do this, (x’, y) is a valid signed message In order to prevent this type of attack, we require that h is collision resistant 16

3. Oscar computes a signature on some message digest z, and then he finds a message x such that z=h(x) If Oscar can do this, (x, y) is a valid signed message In order to prevent this type of attack, we require that h be a preimage hash function 17
![3 El Gamal Signature Scheme n El Gamal Signature Scheme was proposed in 1985 [3] El. Gamal Signature Scheme n El. Gamal Signature Scheme was proposed in 1985](https://slidetodoc.com/presentation_image/e9cef1247d3384b911976ef718e8913b/image-18.jpg)
[3] El. Gamal Signature Scheme n El. Gamal Signature Scheme was proposed in 1985 n The scheme is non-deterministic n Its security is based on Discrete Logarithm Problem n The Discrete Logarithm Problem : given an element β belonging to <α>, find an integer a such that αa= β 18

El. Gamal signature scheme 19

(El. Gamal signature scheme) n n Let p be a prime such that DL problem in Zp is intractable, and let α be a primitive element in Zp * Define K={ (p, α, a, β) : β=αa mod p } p, α, β are the public key, a is the private key For a (secret) random number k, define sigk(x, k)=(γ, δ), where γ=αk mod p and δ=(x-aγ)k-1 mod (p-1) 20

n For a message (γ, δ), define ver (x, (γ, δ))=true iff. βγγδ=αx mod p n If the signature was constructed correctly, the verification will succeed since βγγδ=αa γαkδ = αx mod p By definition of b 21

Example We take p=467, α=2, a=127; then β=2127 mod 467=132 n To sign the message x=100, Alice select k=213; Then γ=2213 mod 467=29, δ=(100 -127*29) * 213 -1 mod 466=51 (100, (29, 51)) is the signed message 22

Since (100, (29, 51)) is valid, Bob will find that βγγδ mod p = 13229 * 2951 mod 467 = 189 is identical with αx mod p = 315 mod 467 = 189 23

Security of the El. Gamal Signature Scheme 1. Selective forgery using a key only attack n Suppose Oscar tries to forge a signature (x, y) for a given message x, without knowing a If he chooses a value γ and the tries to find δ, he must compute δ = logγαxβ-γ mod p It is an instance of DL problem Unsuccessful forgery 24

2. Selective forgery using a key-only attack n If he chooses a value δ and the tries to find γ, he must solve the equation βγγδ mod p = αx mod p for the unknown value γ n It is a problem for which no feasible solution is known Unsuccessful forgery 25

3. Existential forgery using a key only attack n If he chooses a value δ and γ, then tries to find x, he must compute x = logα βγγδ It is an instance of DL problem Unsuccessful forgery 26

4. Existential forgery using a key only attack n Unfortunately, an adversary is able to forge a signed message which can pass the verification Suppose i and j are integers in Zp-1 and gcd(j, p-1), the adversary can assign γ by γ=αiβj mod p According to the above assignment, the verification condition is αx =βγ(αiβj)δ mod p 27

It is equivalent to αx-iδ=βγ+jδ mod p The congruence will be satisfied if x-iδ= 0 mod p-1, and γ+jδ= 0 mod p-1 (1) Given i and j where gcd(j, p-1)=1, we can solve (1) for x and δ 28

Since gcd(j, p-1) γ= αiβj mod p δ= -γj-1 mod p-1 (j-1 exist) x = -γij-1 mod p-1 The adversary constructed a valid signature (x, (γ, δ)) 29

Example Let p=467, α=2, β=132. Suppose the adversary chooses i=99 and j=179 n γ= 299132179 mod 467 δ= -γ* 179 -1 mod 466 x = -γ* 99 * 179 -1 mod 466 = 177 = 41 = 331 It will pass the verification: βγγδ=132117 * 11741 = 303 mod 467 αx = 2231 = 303 mod 467 30

5. Careless use of k will cause attacks: 1. When k is known, an adversary can obtain Alice’s signing key since: a = (x-kδ) *γ-1 mod p-1 31

2. When identical k is used in signing two different messages, an adversary can obtain Alice’s signing key Suppose (x 1, (γ 1, δ 1)) and (x 2, (γ 2, δ 2)) are two signed messages, we have βγγδ 1=αx 1 mod p βγγδ 2=αx 2 mod p Thus αx 1 -x 2=γδ 1 -δ 2 mod p 32

n Suppose γ=αk, then αx 1 -x 2=αk(δ 1 -δ 2) mod p which is equivalent to x 1 -x 2=k(δ 1 -δ 2) mod p-1 n Let d=gcd(δ 1 -δ 2, p-1), define x’=(x 1 -x 2)/d, δ’=(δ 1 -δ 2)/d, p’=(p-1)/d 33

n Then the congruence becomes x’=kδ’ mod p’ thus k=(x’ *δ’-1) + (i * p’) mod p-1, for 0≤i≤d-1 Of these d candidate values, the correct k which is really used by Alice can be determined by testing the condition γ=αk mod p 34

Example We take p=17, α=3, a=8; then β=28 mod 17=16 n Alice first signs x 1=15 using k=5 (15, (5, 11)) Then she signs x 2=10 using k=5 again (10, (5, 10)) 35

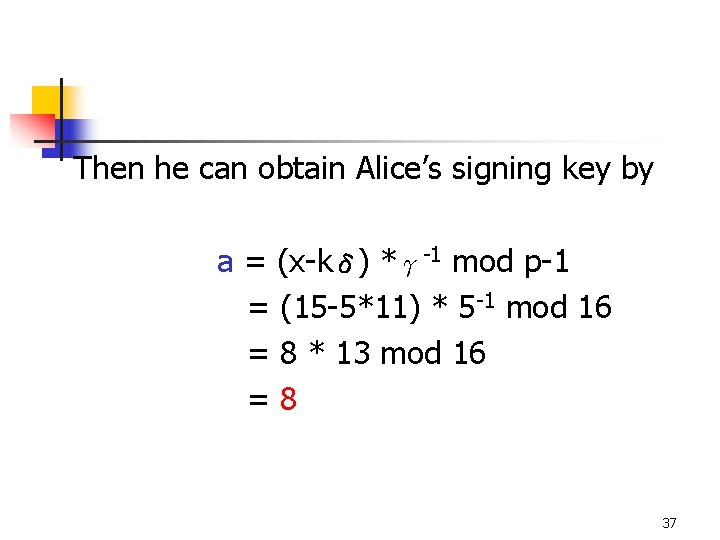
Oscar obtains: (x 1=15, (γ 1=5, δ 1=11)) (x 2=10, (γ 2=5, δ 2=10)) Then he can compute d=gcd(δ 1 -δ 2, p-1)=gcd(1, 16)=1 Thus these is only one candidate value of r k = (x’ *δ’-1) mod p-1 = (5 * 1) mod 16 = 5 36

Then he can obtain Alice’s signing key by a = (x-kδ) *γ-1 mod p-1 = (15 -5*11) * 5 -1 mod 16 = 8 * 13 mod 16 =8 37
 Quotation sandwhich
Quotation sandwhich New and navigation schemes selection of window
New and navigation schemes selection of window Shield punt protection
Shield punt protection Stata graph schemes
Stata graph schemes Pickety fence poem
Pickety fence poem Packaging color schemes
Packaging color schemes Mouse in afrikaans
Mouse in afrikaans Color theory for kids
Color theory for kids Library of congress classification
Library of congress classification Spread punt formation
Spread punt formation Message routing schemes in computer architecture
Message routing schemes in computer architecture Wristband colors meaning hospital
Wristband colors meaning hospital Wecs schemes
Wecs schemes Tricolon
Tricolon Schemes in piaget's theory
Schemes in piaget's theory Ocr past paper mark schemes
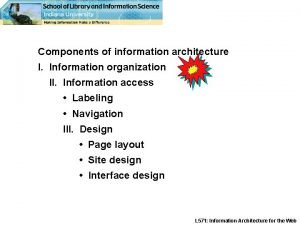
Ocr past paper mark schemes Information architecture organization schemes
Information architecture organization schemes Basic color schemes
Basic color schemes Slsam
Slsam Product classification schemes
Product classification schemes Stata schemes
Stata schemes Classification scheme of a fungus and a bacterium
Classification scheme of a fungus and a bacterium Filling schemes
Filling schemes Pilot relay is used for
Pilot relay is used for Split complementary color scheme
Split complementary color scheme Digital encoding schemes
Digital encoding schemes Rap sentences that rhyme
Rap sentences that rhyme Schools recommendation schemes
Schools recommendation schemes Rhyme scheme
Rhyme scheme Rhyming scheme of a poem
Rhyming scheme of a poem Free verse poem
Free verse poem Rhyme schemes
Rhyme schemes Food assurance schemes
Food assurance schemes Blue adjective
Blue adjective Standards rhyme
Standards rhyme Organization schemes
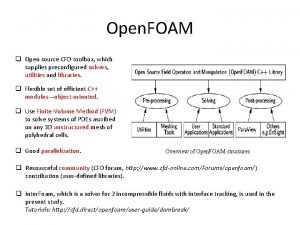
Organization schemes Openfoam interpolation schemes
Openfoam interpolation schemes Albrecht developed the fraud scale
Albrecht developed the fraud scale