Digital Signature 1 Requirements of Digital Signature Efficiency

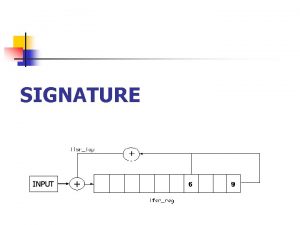
Digital Signature 1

Requirements of Digital Signature Efficiency Unforgeability : only signer can generate Not reusable : not to use for other message Unalterable : No modification of signed message Authentication of a signer Non-repudiation : not denying the act of signing 2

Attack of Digital Signature Hard Easy Key only or no message attack : Adv access only to public parameters and public keys Message attack : Adv has access to pairs of message texts and corresponding signatures. Depending on Adv’s power of selecting messages signed by S. ◦ Known-messages : Adv doesn’t choose message signed by S. ◦ Generic chosen-messages : Adv chooses a set of messages to be signed before knowing the actual S targeted for attack. ◦ Directed chosen-message : Adv chooses a set of messages to be signed after selecting a specific S but the actual attack. ◦ Adaptive chosen-message : Adv chooses message for signing dynamically after inspecting signatures he obtained for previous messages. Adv: Adversary, S: legitimate signer 3

Forgery of Digital Signature Hard Easy Total break : Adv recovers the secret key of S under attack. Universal forgery : Adv doesn’t obtain the secret key of S, but gains the ability to generate valid signatures for any message. Selective forgery : Adv doesn’t obtain the secret key of S, but gains the ability to generate valid signatures for any set of preselected messages. Existential forgery : Adv can create at least one new message and signature pair without knowing the secret key. The messages are only arbitrary bit strings and Adv doesn’t have any power over their composition. 4

Construction of Digital Signature Consists of 6 elements (M, Mh, A, K, S, V) üM : message space üMh (or Ms) : signing space üA : signature space üK : key space üFor K K, signing algorithm sig. K S and its corresponding verification algorithm ver. K V. üEach sig. K : M A üver. K : M x A {t, f} are functions s. t. , ü ver. K(x, y)= t if y = sig. K(x) or ü ver. K(x, y)=f if y sig. K(x) 5

Digital signature with appendix(I) Signature generation (a) get private key, Ks (b) m’=h(m) : hash algorithm and s*=sig. Ks(m’) (c) m, s* : signature Signature verification (a) obtain public key, Kp (b) compute m’=h(m) and u=ver. Kp(m’, s*) (c) accept signature iff u=true. (Ex. ) DSA, El. Gamal, Schnorr 6

Digital signature with appendix(II) (a) signing M m h Mh m’ sig. K A s*=sig. K(m’) (b) verification Mx. A ver. K(m, s*) true false 7

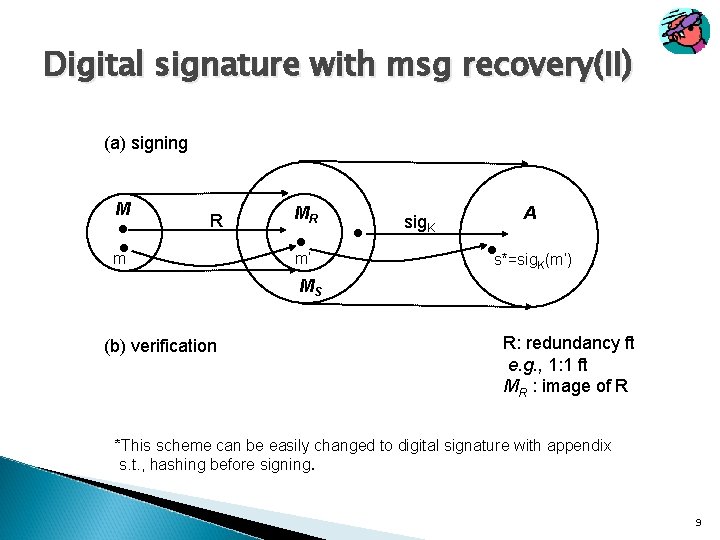
Digital signature with msg recovery(I) Signature generation (a) get private key, Ks (b) m’=R(m) : redundancy function and s*=sig. Ks(m’) (c) s* : signature Signature verification (a) obtain public key KP (b) compute m’= ver. Kp(s*) (c) verify that m’ MR ( if m’ MR, then reject) (d) recover m from m’ by computing R-1(m’) (Ex. ) RSA, Rabin, Nyberg-Rueppel * R() and R-1() are easy to compute. 8

Digital signature with msg recovery(II) (a) signing M R m MR m’ sig. K A s*=sig. K(m’) MS (b) verification R: redundancy ft e. g. , 1: 1 ft MR : image of R *This scheme can be easily changed to digital signature with appendix s. t. , hashing before signing. 9

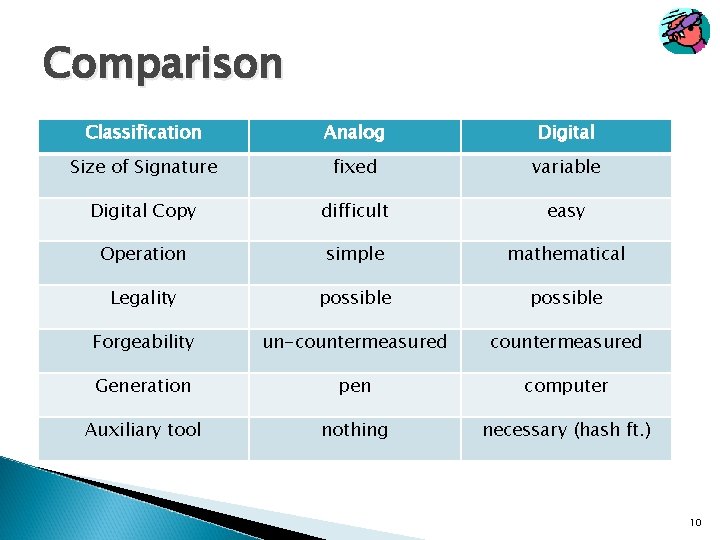
Comparison Classification Analog Digital Size of Signature fixed variable Digital Copy difficult easy Operation simple mathematical Legality possible Forgeability un-countermeasured Generation pen computer Auxiliary tool nothing necessary (hash ft. ) 10

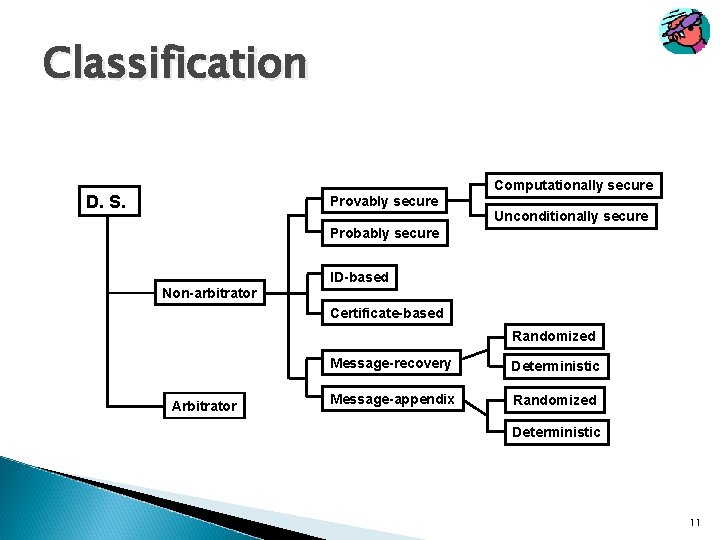
Classification Computationally secure D. S. Provably secure Unconditionally secure Probably secure Non-arbitrator ID-based Certificate-based Randomized Arbitrator Message-recovery Deterministic Message-appendix Randomized Deterministic 11

RSA Signature (preparation) n=pq, M=A= n K ={(n, p, q, e, d) : n=pq, ed=1 mod (n)} public key : {e, n}, private key : {d, p, q} (signing) K=(n, p, q, e, d), sig. K(x)=xd mod n (verification)ver. K(x, y)=true x=ye mod n, x, y n (Problem) If an adversary know signature of x 1 and x 2 to be s 1 and s 2, he can create signature of x 3=x 1 x 2, i. e. , s 3{=s 1 s 2=x 1 d x 2 d= (x 1 x 2)d} without knowing private key, d. To prevent this, hashing before signing or other means must be used. Note that E(m 1)E(m 2)=E(m 1 m 2) in RSA 12

El. Gamal Signature(I) p : prime, p*: primitive element, M = p*, A = p* x p-1* K ={(p, , a, ) : = a mod p} public: (p, , ), private: a (signing) K=(p, , a, ), secret random k p-1* sig. K(m, k) = ( , ) where = k mod p, =(m-a )k-1 mod (p-1) (verification) m, p* and p-1* ver. K(m, , )=true = m mod p * = a k = m mod p 13

El. Gamal Signature(II) (Preparation) p=467, =2, a=127 = a mod p = 2127 mod 467=132 message m=100 random k=213 s. t. , gcd(213, 466)=1. 213 -1 mod 466 =431 signing = k = 2213 mod 467= 29 =(m-a )k-1 mod (p-1)=(100 - 127 x 29) 431 mod 466=51 Verification on m, and = m mod p ? =13229 2951=189 mod 467 m =2100 =189 mod 467 14

El. Gamal Signature(III) Security : without knowing a, forgery of x’s signature is reducible to DLP of finding ( ) chosen ( ). Note ◦ Keep k to be secret ◦ Not to use k two times. Generalization from p* to any finite Abelian group is possible 15

DSS (I) After 1991 August for 3 -year public debate, NIST announced DSS (Digital Signature Standard) documented FIPS-186 in 1994 December. RSA was not selected since its patent Introduce efficient operation under subgroup in El. Gamal signature scheme Used with DHA (Digital Hash Algorithm) 16

DSS(II) p: 512 bit prime, q: 160 bit prime, q|p-1, g p* =g(p-1)/qmod p (q-th root of 1 mod p), M = p*, A= q x q, K={(p, q, , a, ): = a mod p} public: (p, q, , ), private: a. (signing) K=(p, q, , a, ), secret random k (1 k q 1, gcd(k, q)=1), sig. K(m, k) = ( , ) where = ( k mod p) mod q, =(m+a )k-1 mod q. (verification) m p* and , q ver. K(m, , )=true ( e 1 e 2 mod p)mod q = . e 1= m -1 mod q, e 2= -1 mod q. 17

DSS(III) (Ex. ) q=101, p=78 q+1=7879, g=3, = 378 mod 7879 =170, a=75, = a mod 7879 = 4567 (signing) message m=1234, random k=50, k-1 mod 101=99. = ( k mod p) mod q=(17050 mod 7879) mod 101=2518 mod 101=94. =(m+a )k-1 mod q=(1234 +75 x 94) 99 mod 101 = 97. (verification) sig. K(m, k) = ( , ) =(94, 97), m=1234 -1=97 -1 mod 101=25, e 1= m -1 mod q =1234 x 25 mod 101 =45, e 2= -1 mod q = 94 x 25 mod 101 = 27 ( e 1 e 2 mod p)mod q= (17045 4567 27 mod 7879 ) mod 101 = 2518 mod 101=94 ? =94 (valid) 18

Signature Scheme with additional properties 19

Advanced Digital Signature Blind signature One-time signature ◦ Lamport scheme or Bos-Chaum scheme Undeniable signature ◦ Chaum-van Antwerpen scheme Fail-stop signature ◦ van Heyst-Peterson scheme Proxy signature Group (Ring) signature: group member can generate signature if dispute occurs, identify member. etc. 20

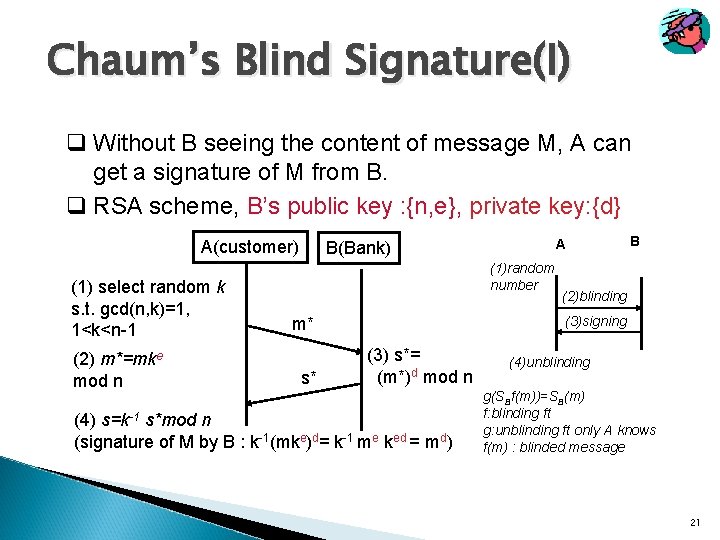
Chaum’s Blind Signature(I) q Without B seeing the content of message M, A can get a signature of M from B. q RSA scheme, B’s public key : {n, e}, private key: {d} A(customer) (1) select random k s. t. gcd(n, k)=1, 1<k<n-1 (2) m*=mke mod n A B(Bank) (1)random number (2)blinding (3)signing m* s* B (3) s*= (m*)d mod n (4) s=k-1 s*mod n (signature of M by B : k-1(mke)d= k-1 me ked = md) (4)unblinding g(SBf(m))=SB(m) f: blinding ft g: unblinding ft only A knows f(m) : blinded message 21

Chaum’s Blind Signature(II) (Preparation) p=11, q=3, n=33, (n)= 10 x 2=20 gcd(d, (n))=1 => d=3, ed =1 mod (n) => 3 d = 1 mod 20 => e=7 B: public key : {n, e}={33, 7}, private key ={d}={3} (1) A’s blinding of m=5 select k s. t. gcd(k, n)=1. gcd(k, 33)=1 => k=2 m* = m ke mod n= 5 27 mod 33 = 640 mod 33 = 13 mod 33 (2) B’s signing without knowing the original m s*= (m*)d mod n = 133 mod 33 =2197 mod 33 =19 mod 33 (3) A’s unblinding s=k-1 s* mod n (2 k-1=1 mod 33 => k=17) = 17 19 mod 33 =323=26 mod 33 * Original Signature : md mod n = 53 mod 33 =125 =26 mod 33 22