Sieve of Eratosthenes Oct 24 2013 copyright 2013

Sieve of Eratosthenes Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 1

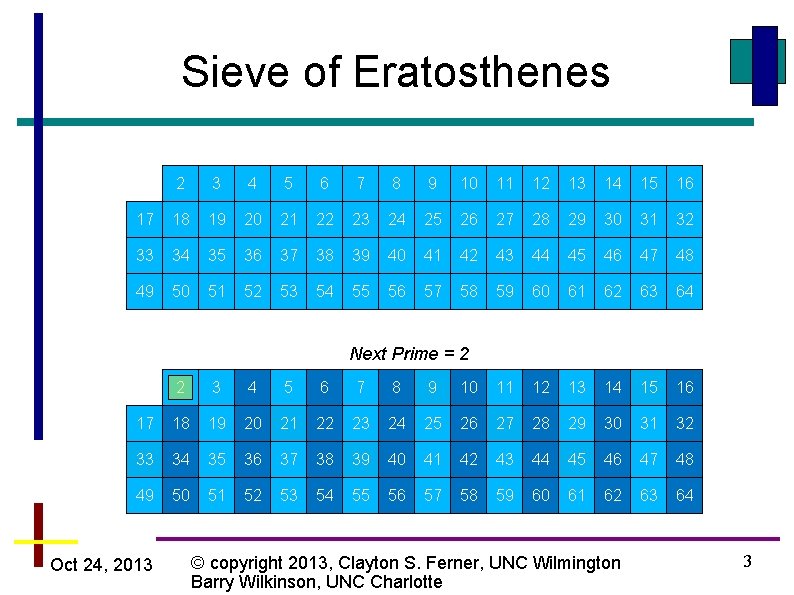
Sieve of Eratosthenes • The Sieve of Eratosthenes is an algorithm to find the prime numbers between 2 and n • Start with an array of booleans from 2 to n initially set to all true • For each known prime starting with 2, mark all the multiples (composites) of that prime • Stop when the next prime > √n • What is left unmark are the primes Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 2

Sieve of Eratosthenes 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Next Prime = 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 3

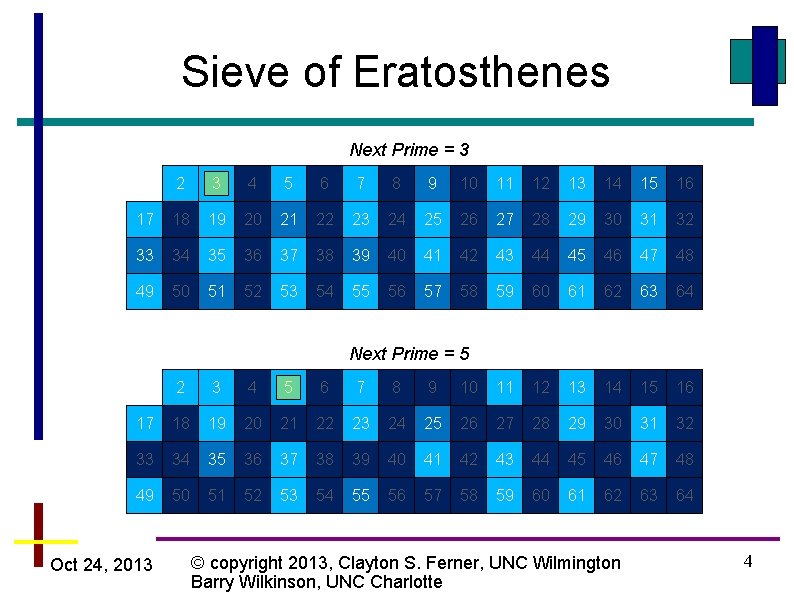
Sieve of Eratosthenes Next Prime = 3 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Next Prime = 5 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 4

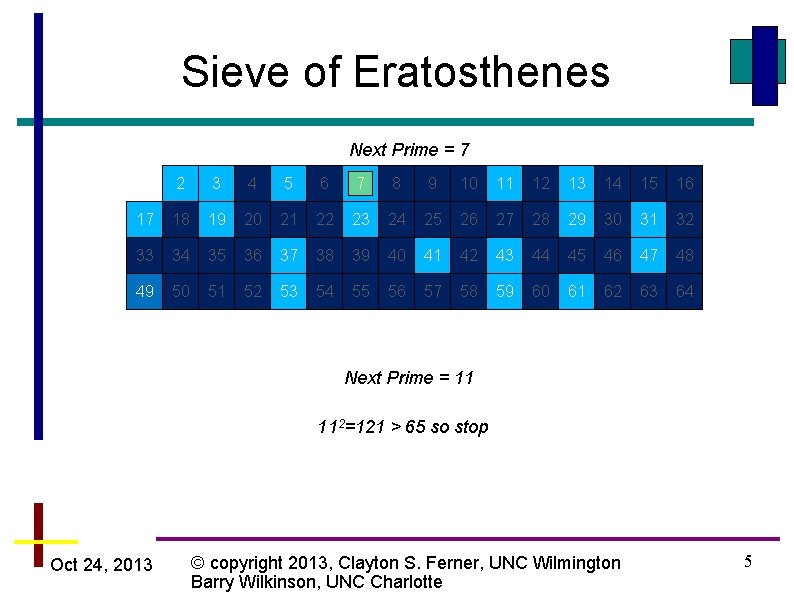
Sieve of Eratosthenes Next Prime = 7 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Next Prime = 11 112=121 > 65 so stop Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 5

Sequential Sieve of Eratosthenes Algorithm (pseudo-code) Sieve_Eratosthenes(int n) { boolean marked [n] = { true, . . . }; prime = 2; while (prime * prime < n) { // or prime < sqrt(n) composite = prime * prime; // start with prime^2 while (composite < n) { marked[composite] = false; composite = composite + prime; // multiples of prime } do { prime++; } while (marked[prime]); // find next prime } Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 6

Sequential Complexity • The outermost loop will iterate at most √n times • The 1 st inner loop could iterate up to n/2 times • The 2 nd loop will iterate √n times total (for all iterations of the outermost loop) • Complexity = Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 7

Parallelizing Sieve of Eratosthenes • An obvious approach is to parallelize the loop marking multiples of prime composite = prime * prime; while (composite < n) { marked[composite] = false; composite = composite + prime; } • We can rewrite this as a for loop: for (composite=prime*prime; composite < n; composite += prime) { marked[composite] = false; Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 8

Parallelizing Sieve of Eratosthenes • Now we have a Scatter/Gather pattern • We only need to broadcast n • We don’t really need to broadcast the initial array “marked” because all processors can initialize it • The difficulty is in selecting the next prime • We have to do a reduction and broadcast of the marked array so all processors can continue updating the array Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 9

Parallelizing Sieve of Eratosthenes Sieve_Eratosthenes(int n) { boolean *marked; #prgama paraguin begin_parallel #pragma paraguin bcast n // Allocate an array of n ints marked = malloc (n * sizeof(int)); for (int i = 0; i < n; i++) marked[i] = 1; // True prime = 2; while (prime * prime < n) { Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 10

Parallelizing Sieve of Eratosthenes composite=prime*prime; We need the loop num. Iterations = n / prime – prime; to be a simple loop #pragma paraguin forall for (i = 0; i < num. Interations; i++) { marked[composite] = false; composite += prime } #pragma paraguin reduce land marked temp // copy temp back into marked #pragma paraguin bcast marked( n ) do { prime++; } while (marked[prime]); Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 11

Parallelizing Sieve of Eratosthenes • A better approach is to partition the array instead of the loop • With p processors, each processor is responsible for elements of the array • It is the master process’ responsibility to determine the next prime • This need to be broadcast, but we can eliminate the reduction • Also, only a single integer needs to be broadcast instead of an array Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 12

Sieve of Eratosthenes √n primes will be used. These need to be within the master process’ region. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 p 0 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 p 1 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 p 2 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 p 3 Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 13

Parallelizing Sieve of Eratosthenes • First we need to make sure the master process will compute √n values • The master process needs to be able to determine all values used for prime #pragma paraguin begin_parallel proc 0_size = (n-1)/__guin_NP; if (2 + proc 0_size < (int) sqrt((double) n)) { if (__guin_rank == 0) printf (“Too many processorsn”); return 1; } Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 14

Parallelizing Sieve of Eratosthenes low_value = (__guin_rank*n-1)/__guin_NP; high_value = ((rank+1)*n-1)/__guin_NP; prime = 2; do { Partition the array: each processor is responsible for values from low to high Compute the first multiple of prime greater to or equal to low_value if (low_value % prime == 0) first = low_value; else first = low_value + prime – (low_value%prime); Mark multiple of prime in each processor’s range for (i=first + prime; i < high_value; i += prime) marked[i] = false; Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 15

Parallelizing Sieve of Eratosthenes if (__guin_rank == 0) { do { prime++; } while (marked[prime]); } Master determines next prime and broadcasts it. #pragma paraguin bcast prime } while (prime * prime < n); No reduction is needed until we finish the computation #pragma paraguin gather marked( n ) Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 16

Parallel Complexity • The outermost loop will iterate √n times • The 1 st inner loop could iterate up to n/2 p times with p processors • The 2 nd loop will iterate √n times total (for all iterations of the outermost loop) • The broadcast take log(p) time • Complexity = Computation Oct 24, 2013 Communication © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 17

Improving the Parallel Algorithm • Still we have a broadcast within the outermost loop • How can we eliminate that? • Can we have all processors determine what the next prime is? Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 18

Improving the Parallel Algorithm • The number of primes used in the Sieve of Eratosthenes is √n • All processors compute the primes from 2 … √n • Now all processors have their own private copy of the primes used • We can eliminate the broadcast • As well as the requirement that the master process’ section be at least √n Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 19

Complexity • The complexity is essentially the same for most processors, except: – Communication is eliminated until the end – There is added complexity to compute the first √n primes sequentially • Complexity to compute the first √n primes: Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 20

Complexity • Final Complexity: • Implementation left as an exercise Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 21

Questions Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 22

Discussion Question • Question: Would it be better to implement this algorithm in shared-memory (using Open. MP) than distributed-memory (using MPI)? Oct 24, 2013 © copyright 2013, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 23