Whats coming up Oct 25 Oct 27 Oct

What’s coming up? ? ? • • • • Oct 25 Oct 27 Oct 29 Nov 1 Nov 3, 5 Nov 8, 10 Nov 12, 15 Nov 17 Nov 19 Nov 22 Nov 24 Nov 26 Nov 29 Dec 1 Dec 2 The atmosphere, part 1 Midterm … No lecture The atmosphere, part 2 Light, blackbodies, Bohr Postulates of QM, p-in-a-box Hydrogen and multi – e atoms Multi-electron atoms Periodic properties Valence-bond; Lewis structures Hybrid orbitals; VSEPR MO theory Review for exam Ch. 8 Ch. 9, 10 Ch. 11, 12 Ch. 12

• We can split the hydrogen wavefunction into two: Y(x, y, z) Y(r, q, j) = R(r) x Y(q, j) Depends on r only Depends on angular variables

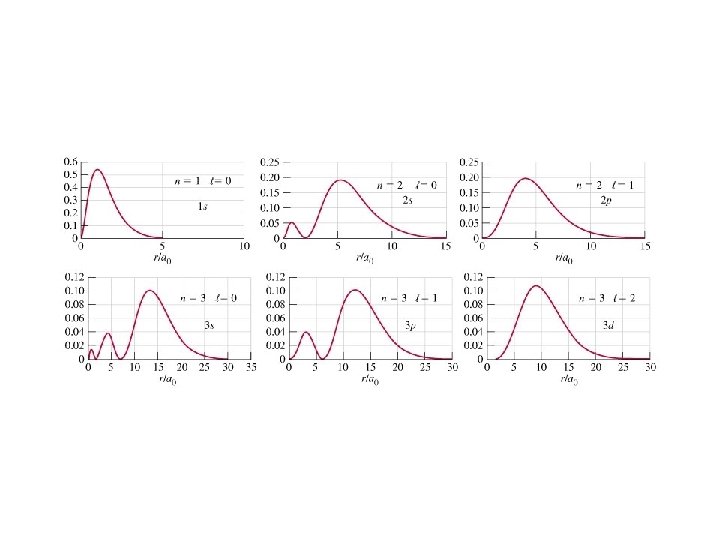
• The solutions have the same features we have seen already: – Energy is quantized • En = - R Z 2 / n 2 = - 2. 178 x 10 -18 Z 2 / n 2 J [ n = 1, 2, 3 …] – Wavefunctions have shapes which depend on the quantum numbers – There are (n-1) nodes in the wavefunctions

• Because we have 3 spatial dimensions, we end up with 3 quantum numbers: n, l, ml • n = 1, 2, 3, …; l = 0, 1, 2 … (n-1); ml = -l, -l+1, … 0…l-1, l • n is the principal quantum number – gives energy and level • l is the orbital angular momentum quantum number – it gives the shape of the wavefunction • ml is the magnetic quantum number – it distinguishes the various degenerate wavefunctions with the same n and l

• E n = - R Z 2 / n 2 = - 2. 178 x 10 -18 Z 2 / n 2 J [ n = 1, 2, 3 …] … degenerate

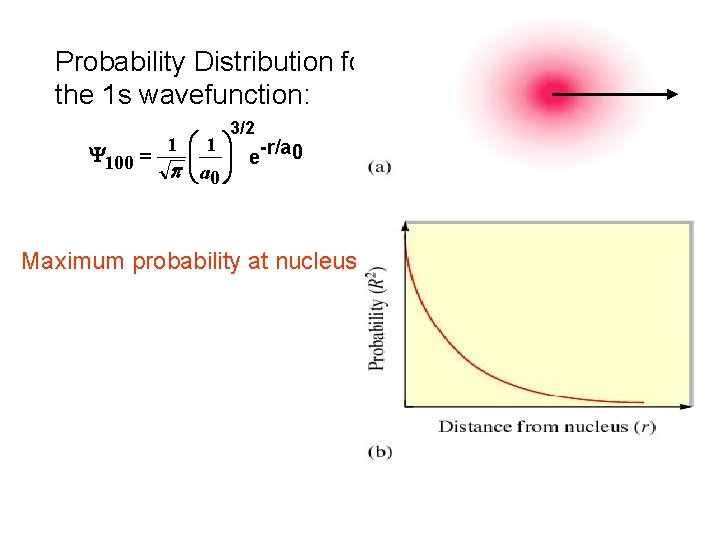
Probability Distribution for the 1 s wavefunction: 3/2 1 æ 1 ö -r/a 0 çç ÷÷ e Y 100 = p è a 0 ø Maximum probability at nucleus

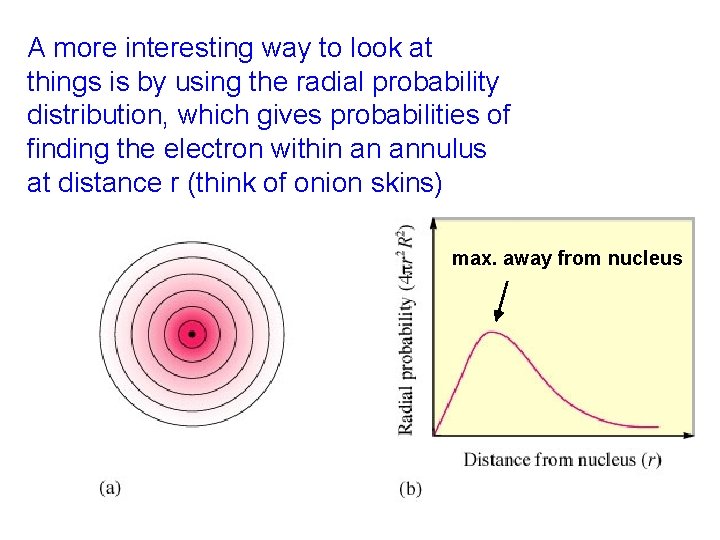
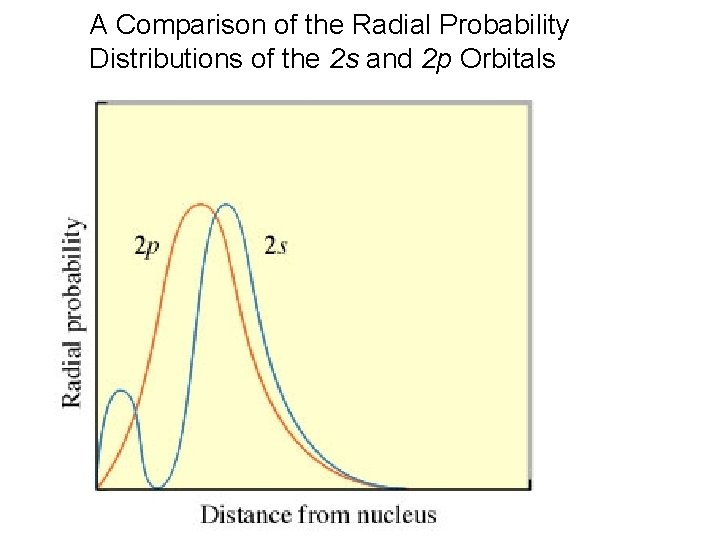
A more interesting way to look at things is by using the radial probability distribution, which gives probabilities of finding the electron within an annulus at distance r (think of onion skins) max. away from nucleus

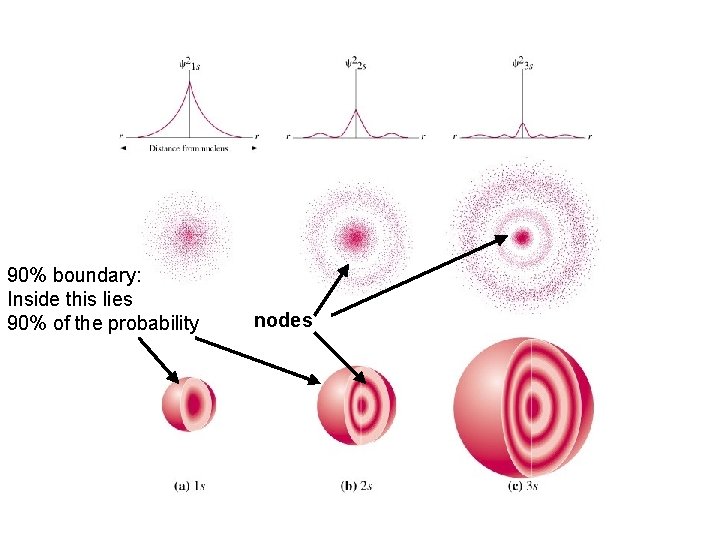
90% boundary: Inside this lies 90% of the probability nodes

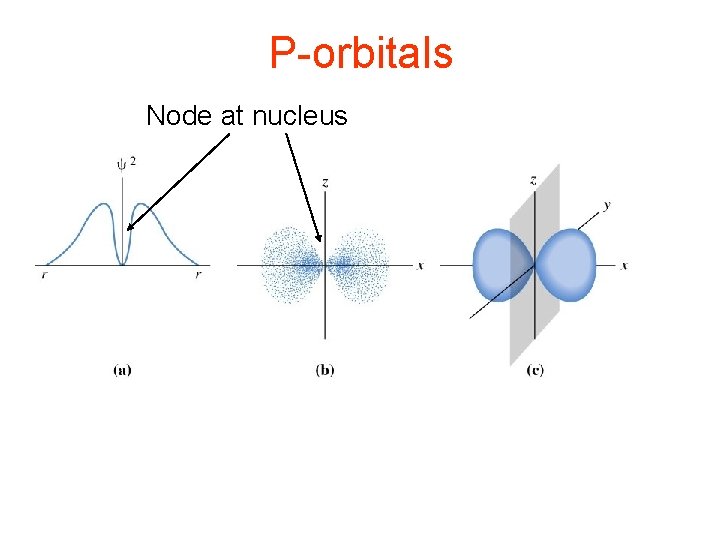
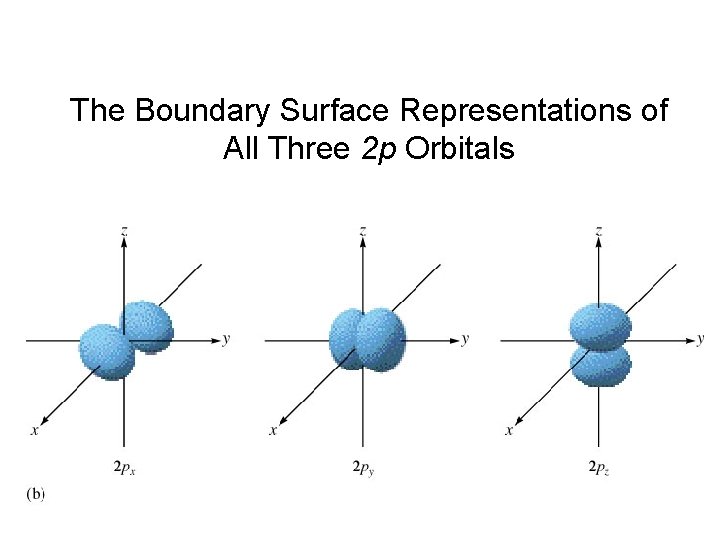
P-orbitals Node at nucleus

The result (after a lot of math!) Node at s = 2!! Nodes at f, q = 0 !!

The Boundary Surface Representations of All Three 2 p Orbitals

A Comparison of the Radial Probability Distributions of the 2 s and 2 p Orbitals

A Cross Section of the Electron Probability Distribution for a 3 p Orbital Spatial nodes and Angular nodes!

Nodes at f, q = 0 !! Nodes at s = 0 and 4

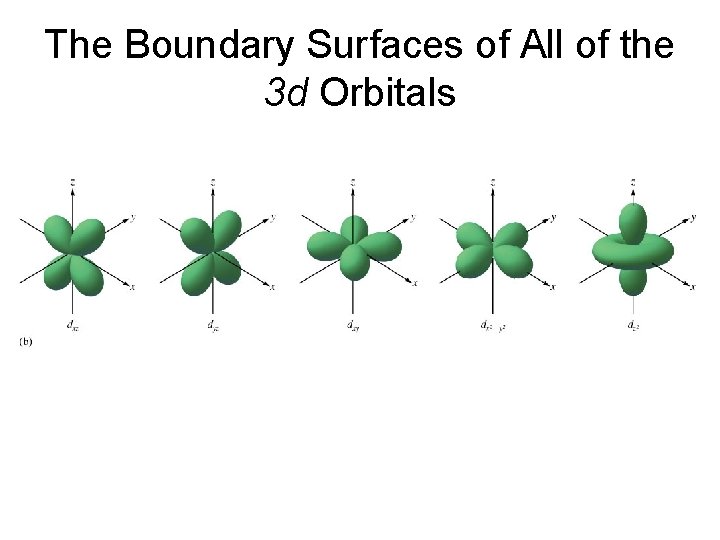
The Boundary Surfaces of All of the 3 d Orbitals

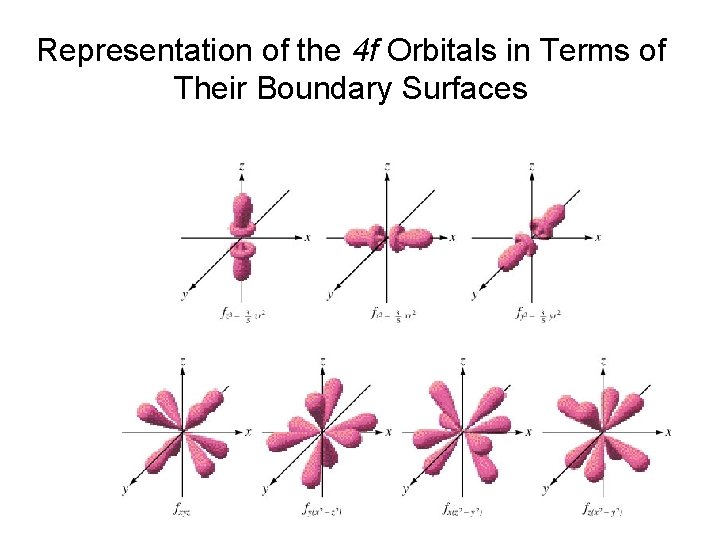
Representation of the 4 f Orbitals in Terms of Their Boundary Surfaces

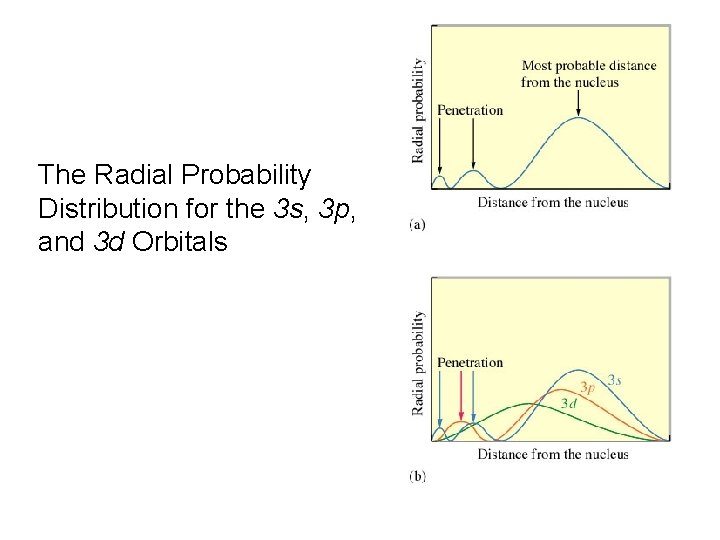
The Radial Probability Distribution for the 3 s, 3 p, and 3 d Orbitals

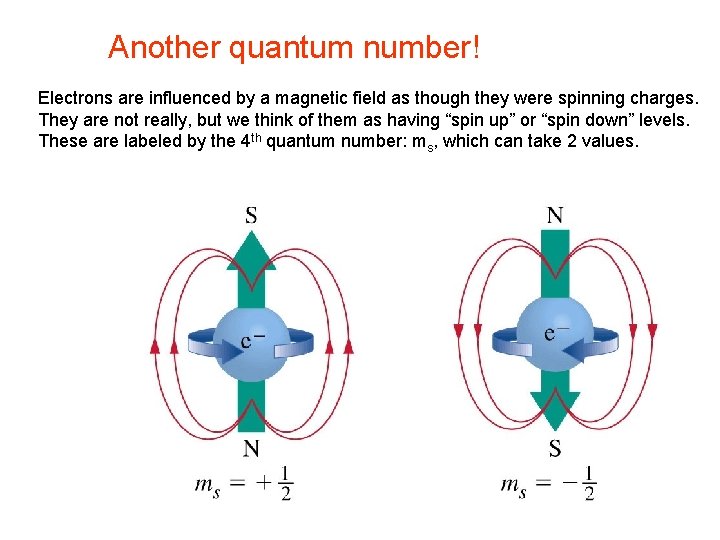
Another quantum number! Electrons are influenced by a magnetic field as though they were spinning charges. They are not really, but we think of them as having “spin up” or “spin down” levels. These are labeled by the 4 th quantum number: ms, which can take 2 values.

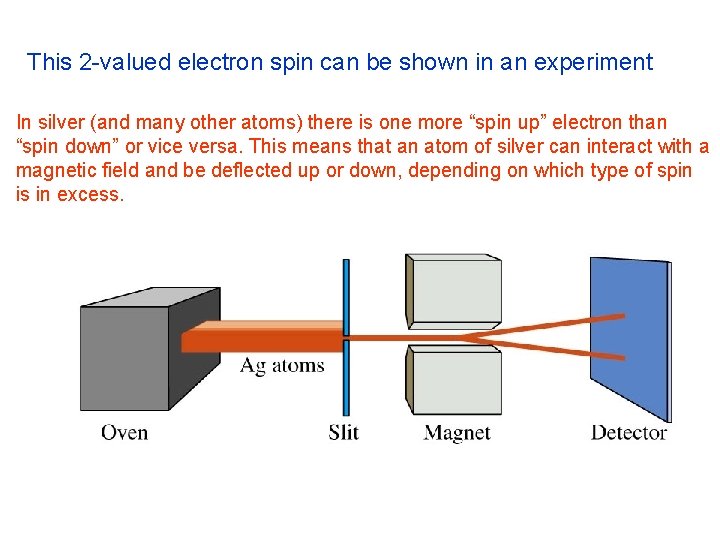
This 2 -valued electron spin can be shown in an experiment In silver (and many other atoms) there is one more “spin up” electron than “spin down” or vice versa. This means that an atom of silver can interact with a magnetic field and be deflected up or down, depending on which type of spin is in excess.

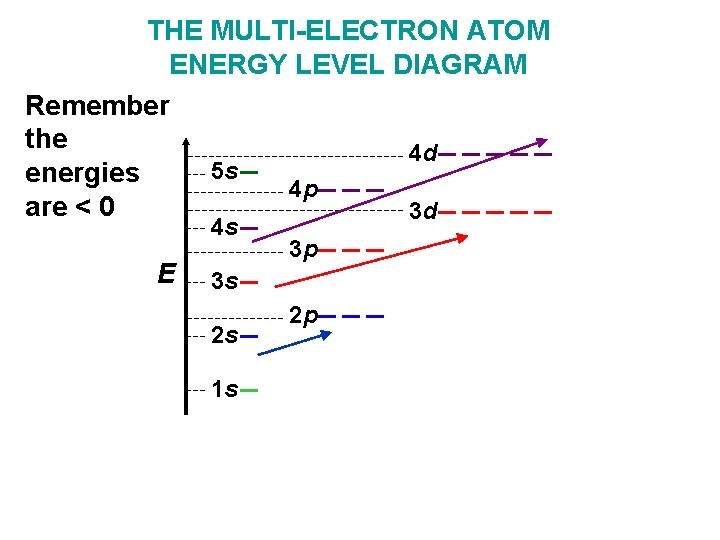
In multi-electron atoms things change, because of the influence of electrons which are already there E Remember the energies are <0 3 s 3 p 2 s 2 p 3 d 1 s The degenerate energy levels are changed somewhat to become

THE MULTI-ELECTRON ATOM ENERGY LEVEL DIAGRAM Remember the 4 d 5 s energies 4 p are < 0 3 d 4 s E 3 p 3 s 2 s 1 s 2 p

THE PAULI PRINCIPLE No two electrons in the same atom can have the same set of four quantum numbers (n, l, ml , ms). An orbital is described by three quantum numbers, Then each electron in a given orbital must have a different ms HOW MANY ELECTRONS IN AN ORBITAL? each orbital may contain a maximum of two electrons, and they must have opposite spins.

ELECTRONIC CONFIGURATIONS THE BUILDING-UP PRINCIPLE. GROUND STATE lowest energy electronic configuration assign electrons to orbitals one at a time Electrons go into the available orbital of lowest energy. Electrons are placed in orbitals according to the Pauli Principle. A maximum of two electrons per orbital.

THE AUFBAU (BUILDING-UP) PRINCIPLE: electrons are added to hydrogen-like atomic orbitals in order of increasing energy 5 s 4 s E 4 d 4 p 3 d 3 p 3 s 2 s 2 p 1 s The electron configuration of any atom or ion…. . can be represented by an orbital diagram

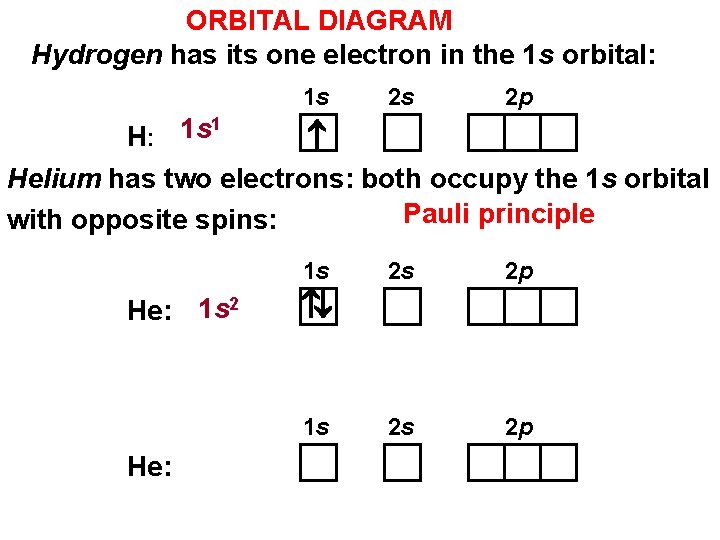
ORBITAL DIAGRAM Hydrogen has its one electron in the 1 s orbital: 1 s 2 s 2 p 1 1 s H: Helium has two electrons: both occupy the 1 s orbital Pauli principle with opposite spins: 1 s He: 1 s 2 2 p 2 s 2 p 1 s He: 2 s

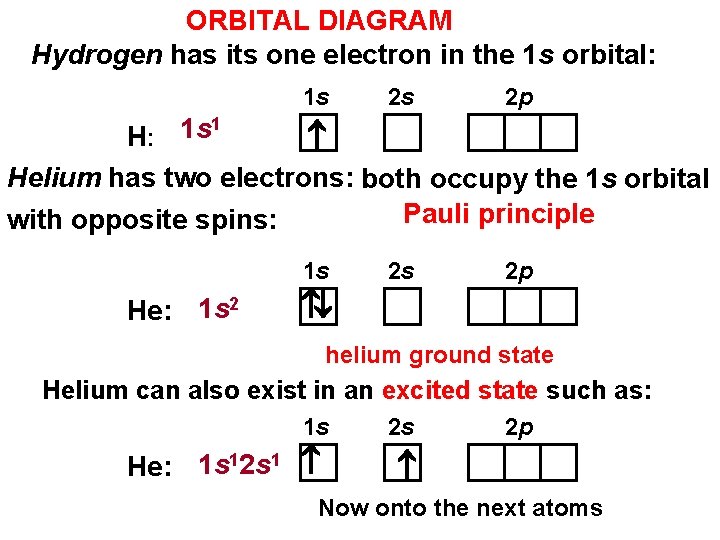
ORBITAL DIAGRAM Hydrogen has its one electron in the 1 s orbital: 1 s 2 s 2 p 1 1 s H: Helium has two electrons: both occupy the 1 s orbital Pauli principle with opposite spins: 1 s He: 1 s 2 2 s 2 p helium ground state Helium can also exist in an excited state such as: 1 s He: 1 s 12 s 1 2 s 2 p Now onto the next atoms

Lithium has three electrons, so it must use the 2 s orbital: 1 s Li: 2 s 2 p 1 s 22 s 1 Beryllium has four electrons, which fill both the 1 s and 2 s orbitals: 1 s 2 s 2 p Be: 1 s 2 2 s 2 Boron’s five electrons fill the 1 s and 2 s orbitals, and begin to fill the 2 p orbitals. Since all three are degenerate, the order in which they are filled does not matter. 1 s B: 1 s 22 p 1 2 s 2 p

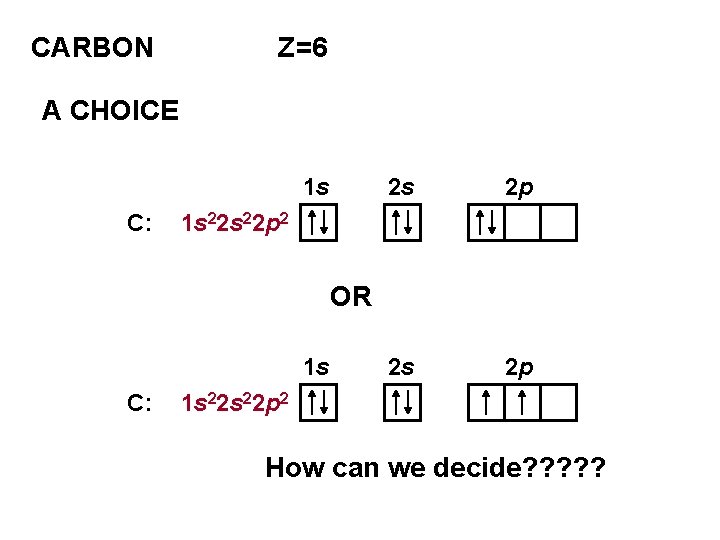
CARBON Z=6 A CHOICE 1 s C: 2 s 2 p 1 s 22 p 2 OR 1 s C: 1 s 22 p 2 How can we decide? ? ?

HUND’S RULE FOR THE GROUND STATE ELECTRONS OCCUPY DEGENERATE ORBITALS SEPARATELY THE SPINS ARE PARALLEL SO FOR CARBON THE GROUND STATE IS 1 s C: 1 s 22 p 2 2 s 2 p

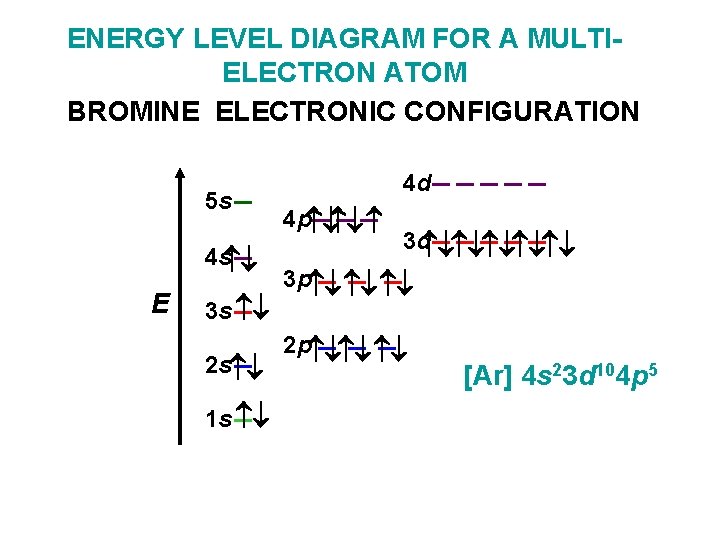
ENERGY LEVEL DIAGRAM FOR A MULTIELECTRON ATOM BROMINE ELECTRONIC CONFIGURATION 5 s 4 s E 3 s 2 s 1 s 4 d 4 p 3 d 3 p 2 p [Ar] 4 s 23 d 104 p 5

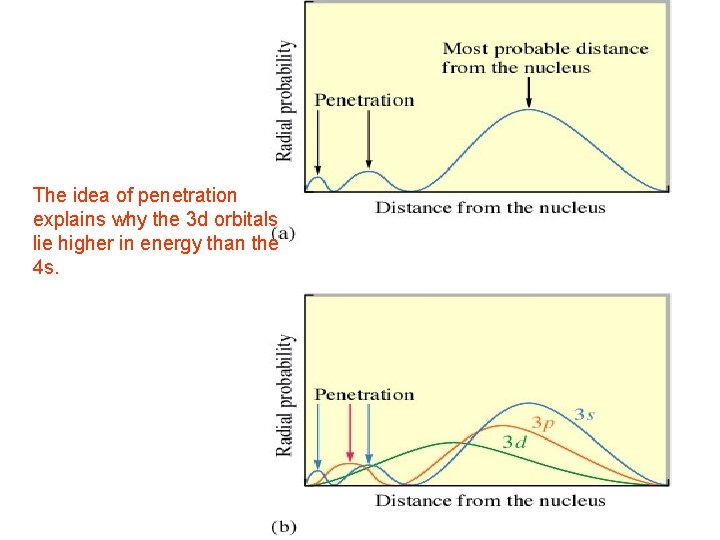
The idea of penetration explains why the 3 d orbitals lie higher in energy than the 4 s.

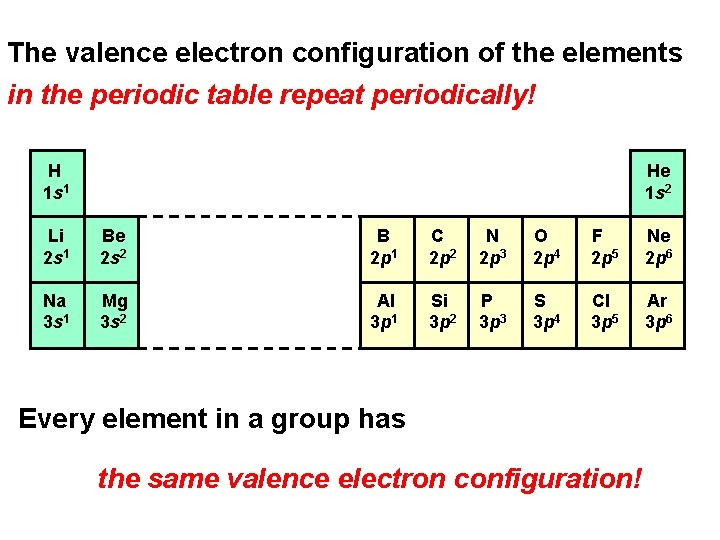
The valence electron configuration of the elements in the periodic table repeat periodically! H 1 s 1 He 1 s 2 Li 2 s 1 Be 2 s 2 B 2 p 1 C 2 p 2 N 2 p 3 O 2 p 4 F 2 p 5 Ne 2 p 6 Na 3 s 1 Mg 3 s 2 Al 3 p 1 Si 3 p 2 P 3 p 3 S 3 p 4 Cl 3 p 5 Ar 3 p 6 Every element in a group has the same valence electron configuration!