Set and Sets Operations Lecturer Shaykhah 1 Set

Set and Sets Operations Lecturer: Shaykhah 1

Set definition Set is the fundamental discrete structure on which all other discrete structures are built. Sets are used to group objects together. Often, the objects in a set have similar properties. A set is an unordered collection of objects. The objects in a set are called the elements, or members, of the set Lecturer: Shaykhah 2

Some Important Sets The set of natural numbers: N = {0, 1, 2, 3, . . . } The set of integers: Z = {. . . , − 2, − 1, 0, 1, 2, . . . } The set of positive integers: Z+ = {1, 2, 3, . . . } The set of fractions: Q = {0, ½, – 5, 78/13, …} Q ={p/q | pЄ Z , qЄZ, and q≠ 0 } The set of Real: R = {– 3/2, 0, e, π2, sqrt(5), …} Lecturer: Shaykhah 3

Notation used to describe membership in sets n n n a set A is a collection of elements. If x is an element of A, we write x A; If not: x A Say: “x is a member of A” or “x is in A”. Note: Lowercase letters are used for elements, capitals for sets. Two sets are equal if and only if they have the same elements A= B : x( x A x B) also § Two sets A and B are equal if A B and B A. § So to show equality of sets A and B, show: § § A B B A Lecturer: Shaykhah 4

How to describe a set? List all the members of a set, when this is possible. We use a notation where all members of the set are listed between braces. { } Example : {dog, cat, horse} Sometimes the brace notation is used to describe a set without listing all its members. Some members of the set are listed, and then ellipses (. . . ) are used when the general pattern of the elements is obvious. Example: The set of positive integers less than 100 can be denoted by {1, 2, 3, . . . , 99}. Lecturer: Shaykhah 5

How to describe a set? Another way to describe a set is to use set builder notation. We characterize all those elements in the set by stating the property or properties they must have to be members. Example: the set O of all odd positive integers less than 10 can be written as: O = {x | x is an odd positive integer <10} or, specifying the universe as the set of positive integers, as O = {x Z+ | x is odd and x<10}. Lecturer: Shaykhah 6

Sets The Empty Set (Null Set) We use to denote the empty set, i. e. the set with no elements. For example: the set of all positive integers that are greater than their squares is the null set. Singleton set A set with one element is called a singleton set. Lecturer: Shaykhah 7

Sets Computer Science Note that the concept of a datatype, or type, in computer science is built upon the concept of a set. In particular, a datatype is the name of a set, together with a set of operations that can be performed on objects from that set. For example, Boolean is the name of the set {0, 1} together with operators on one or more elements of this set, such as AND, OR, and NOT. Lecturer: Shaykhah 8

Module #3 - Sets Computer Representation of Sets • Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. The bit string (of length |U| = 10) that represents the set A = {1, 3, 5, 6, 9} has a one in the first, third, fifth, sixth, and ninth position, and zero elsewhere. It is 1 0 1 1 0 0 1 0. 12/16/2021 (c)2001 -2003, Michael P. Frank

Sets Venn diagrams q Sets can be represented graphically using Venn diagrams. q In Venn diagrams the universal set U, which contains all the objects under consideration, is represented by a rectangle. q Inside this rectangle, circles or other geometrical figures are used to represent sets. q Sometimes points are used to represent the particular elements of the set. Lecturer: Shaykhah 10

Sets Example: A Venn diagram that represents V = {a, e, i, o, u}, the set of vowels in the English alphabet Lecturer: Shaykhah 11

Subset q q q The set A is said to be a subset of B if and only if every element of A is also an element of B. We use the notation A B to indicate that A is a subset of the set B. We see that A B if and only if the quantification x (x A → x B) is true. Lecturer: Shaykhah 12

Subsets For every set S, 1. S 2. S S Proper subset: When a set A is a subset of a set B but A ≠ B, A B, and A B. We write A B and say that A is a proper subset of B For A B to be true, it must be the case that x ((x A) (x B)) x ((x B) (x A)) Lecturer: Shaykhah 13

Subsets Quick examples: {1, 2, 3} {1, 2, 3, 4, 5} Is {1, 2, 3}? Is { , 1, 2, 3}? Yes! Lecturer: Shaykhah Because to conclude it isn’t a subset we have to find an element in the null set that is not in the set {1, 2, 3}. Which is not the case No! Yes! 14

Subsets Quiz Time: Is {x} {x, {x}}? Yes! Is {x} {x}? No! Lecturer: Shaykhah 15

Finite and Infinite Sets Finite set q Let S be a set. If there are exactly n distinct elements in S where n is a nonnegative integer, we say that S is a finite set and that n is the cardinality of S. q The cardinality of S is denoted by |S|. q |A B| = |A| + |B| - |A B| Infinite set A set is said to be infinite if it is not finite. For example, the set of positive integers is infinite. Lecturer: Shaykhah 16

Cardinality Find S = {1, 2, 3}, S = {3, 3, 3}, S = { , { }, { }} }, S = {0, 1, 2, 3, …}, Lecturer: Shaykhah |S| = 3. |S| = 1. |S| = 0. |S| = 3. |S| is infinite 17

Sets Ways to Define Sets: Explicitly: {John, Paul, George, Ringo} Implicitly: {1, 2, 3, …}, or {2, 3, 5, 7, 11, 13, 17, …} Set builder: { x : x is prime }, { x | x is odd }. In general { x : P(x) is true }, where P(x) is some description of the set. Lecturer: Shaykhah 18

The power of a set q Many problems involve testing all combinations of elements of a set to see if they satisfy some property. q To consider all such combinations of elements of a set S, we build a new set that has as its members all the subsets of S. q Given a set S, the power set of S is the set of all subsets of the set S. The power set of S is denoted by P(S). q if a set has n elements , then the power has 2 n elements Lecturer: Shaykhah 19

The power of a set Example: What is the power set of the set {0, 1, 2}? P({0, 1, 2}) is the set of all subsets of {0, 1, 2} P({0, 1, 2})= { , {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}} What is the power set of the empty set? What is the power set of the set { } P( )= { } N. B. the power set of any subset has at least two P({ })= { , { }} Lecturer: Shaykhah elements The null set and the set itself 20

The Power Set Quick Quiz: Find the power set of the following: S = {a}, P(S)= { , {a}}. S = {a, b}, P(S) = { , {a}, {b}, {a, b}}. S = , P(S) = { }. S = { , { }}, P(S) = { , { }, {{ }}, { }}}. Lecturer: Shaykhah 21

Cartesian Products q The order of elements in a collection is often important. q Because sets are unordered, a different structure is needed to represent ordered collections. q This is provided by ordered n-tuples. q The ordered n-tuple (a 1, a 2, . . . , an) is the ordered collection that has a 1 as its first element, a 2 as its second element, . . . , and an as its nth element. Lecturer: Shaykhah 22

Cartesian Products q Let A and B be sets. The Cartesian product of A and B, denoted by A×B, is the set of all ordered pairs (a, b), where a A and b B. A×B = {(a, b) | a A b B}. A 1×A 2×…×An= {(a 1, a 2, …, an) | ai Ai for i=1, 2, …, n}. q A×B not equal to B×A Lecturer: Shaykhah 23

Cartesian Products Example: What is the Cartesian product A × B × C, where A = {0, 1}, B = {1, 2}, and C = {0, 1, 2}? Solution: Ax. Bx. C = {(0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 2, 0), (0, 2, 1), (0, 2, 2), (1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 2, 0), (1, 2, 1), (1, 2, 2)} Lecturer: Shaykhah 24

Notation with Quantifiers Whenever we wrote x. P(x) or x. P(x), we specified the universe of using explicit English language Now we can simplify things using set notation! Example x R (x 2 0) x Z (x 2=1) Also mixing quantifiers: a, b, c R x C(ax 2+bx+c=0) Lecturer: Shaykhah 25

Sets Operations Lecturer: Shaykhah 26

UNION The union of two sets A and B is: A B = { x : x A v x B} If A = {1, 2, 3}, and B = {2, 4}, then A B = {1, 2, 3, 4} B Lecturer: Shaykhah A 27

Intersection The intersection of two sets A and B is: A B = { x : x A x B} If A = {Charlie, Lucy, Linus}, and B = {Lucy, Desi}, then A B = {Lucy} B Lecturer: Shaykhah A 28

Intersection If A = {x : x is a US president}, and B = {x : x is deceased}, then A B = {x : x is a deceased US president} B Lecturer: Shaykhah A 29

Disjoint If A = {x : x is a US president}, and B = {x : x is in this room}, then A B = {x : x is a US president in this room} = B Lecturer: Shaykhah A Sets whose intersection is empty are called disjoint sets 30

Complement The complement of a set A is: A = A’ = { x : x A} If A = {x : x is bored}, then A = {x : x is not bored} = U A B=B A A =U and U= Lecturer: Shaykhah 31

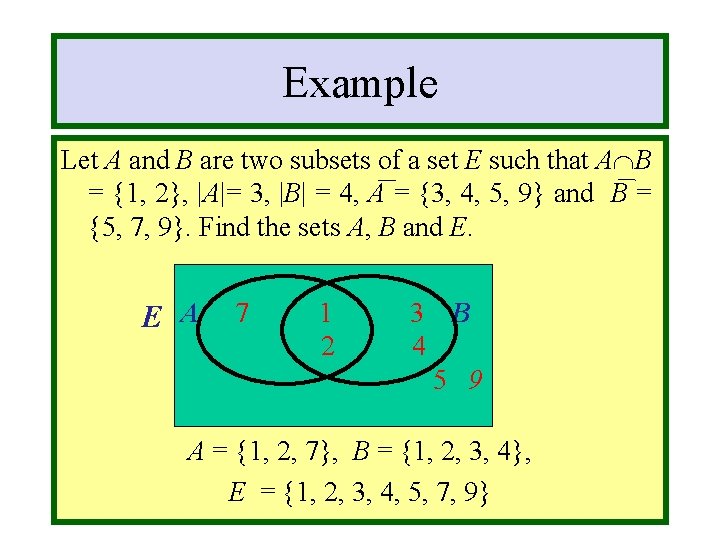
Module #3 - Sets Example Let A and B are two subsets of a set E such that A B = {1, 2}, |A|= 3, |B| = 4, A = {3, 4, 5, 9} and B = {5, 7, 9}. Find the sets A, B and E. E A 7 1 2 3 B 4 5 9 A = {1, 2, 7}, B = {1, 2, 3, 4}, E = {1, 2, 3, 4, 5, 7, 9} 12/16/2021 (c)2001 -2003, Michael P. Frank

Difference The set difference, A - B, is: U A B A-B={x: x A x B} A-B=A B Lecturer: Shaykhah 33

Symmetric Difference Like “exclusive or” The symmetric difference, A B, is: A B = { x : (x A x B) v (x B x A)} = (A - B) U (B - A) U A B Lecturer: Shaykhah 34

Symmetric Difference Example Let A = {1, 2, 3, 4, 5, 6, 7} B = {3, 4, p, q, r, s} Then we have A U B = {1, 2, 3, 4, 5, 6, 7, p, q, r, s} A B = {3, 4} We get A B = {1, 2, 5, 6, 7, p, q, r, s} Lecturer: Shaykhah 35

Proving Set Equivalences • Recall that to prove such identity, we must show that: 1. 2. 3. • • The left-hand side is a subset of the right-hand side The right-hand side is a subset of the left-hand side Then conclude that the two sides are thus equal The book proves several of the standard set identities. We will give a couple of different examples here. Lecturer: Shaykhah 36

Proving Set Equivalences: Example A (1) Let A={x|x is even} B={x|x is a multiple of 3} C={x|x is a multiple of 6} Show that A B=C Lecturer: Shaykhah 37

Proving Set Equivalences: Example A (2) A B C: x A B x is a multiple of 2 and x is a multiple of 3 we can write x=2. 3. k for some integer k x=6 k for some integer k x is a multiple of 6 x C C A B: x C x is a multiple of 6 x =6 k for some integer k x=2(3 k)=3(2 k) x is a multiple of 2 and of 3 x A B Lecturer: Shaykhah 38

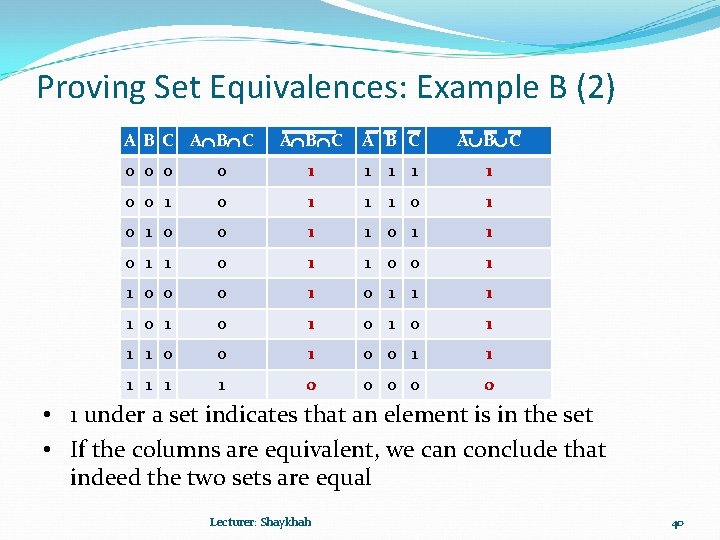
Proving Set Equivalences: Example B (1) An alternative prove is to use membership tables where an entry is 1 if a chosen (but fixed) element is in the set 0 otherwise Example: Show that A B C=A B C Lecturer: Shaykhah 39

Proving Set Equivalences: Example B (2) A B C A B C 0 0 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 • 1 under a set indicates that an element is in the set • If the columns are equivalent, we can conclude that indeed the two sets are equal Lecturer: Shaykhah 40

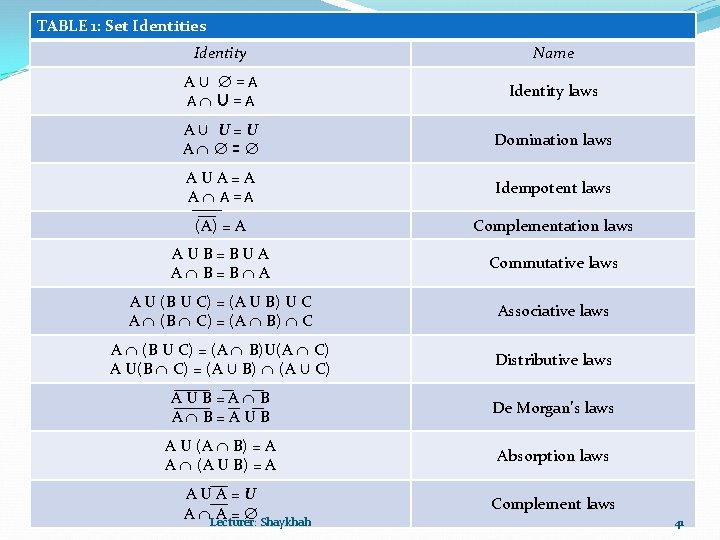
TABLE 1: Set Identities Identity Name AU =A A U =A Identity laws AU U=U A = Domination laws AUA=A A A=A Idempotent laws (A) = A Complementation laws AUB=BUA A B=B A Commutative laws A U (B U C) = (A U B) U C A (B C) = (A B) C Associative laws A (B U C) = (A B)U(A C) A U(B C) = (A U B) (A U C) Distributive laws AUB=A B A B=AUB De Morgan’s laws A U (A B) = A A (A U B) = A Absorption laws AUA=U A Lecturer: A = Shaykhah Complement laws 41

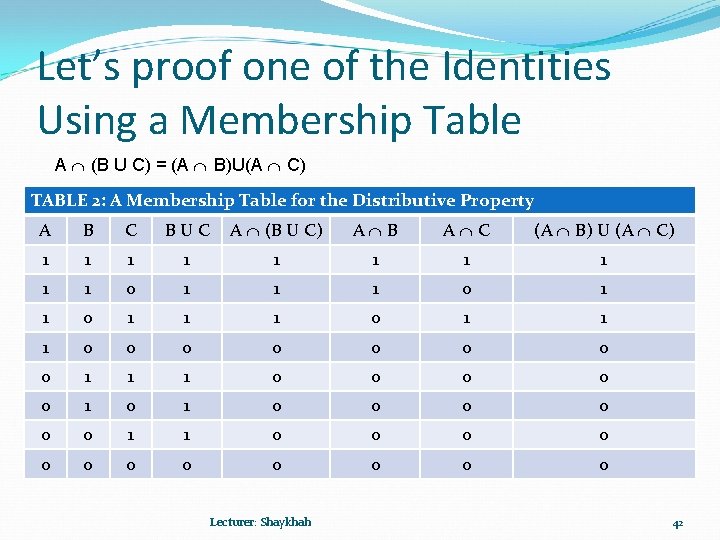
Let’s proof one of the Identities Using a Membership Table A (B U C) = (A B)U(A C) TABLE 2: A Membership Table for the Distributive Property A B C BUC A (B U C) A B A C (A B) U (A C) 1 1 1 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 Lecturer: Shaykhah 42

ANY QUESTIONS? ? ? Refer to chapter 2 of the book for further reading Lecturer: Shaykhah 43